运用“合成与分解”思想巧解复杂的运动问题

姜葛 张云莹

(北京市昌平区教师进修学校)

1 问题提出

“合成与分解”思想是高中物理中重要的思维方法.任何运动都可以分解为两个分运动,如平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动;斜抛运动可以分解为水平方向的匀速直线运动和竖直方向的匀变速直线运动;静止也可以分解为两个速度方向相反、大小相等的匀速直线运动.运动合成与分解遵循矢量的运算法则,即平行四边形定则.运动的合成与分解本质上是描述运动的物理量,即位移、速度、加速度的合成与分解.利用合成与分解的观点可以分析、解决物理中复杂的运动问题.

2 重力场中复杂的运动问题

在重力场中研究物体的运动是高中物理中常见的问题.在重力场中物体受到竖直方向的重力作用.

例1如图1所示,一高度为h、内壁光滑的圆筒竖直放置,将一个小滑块在圆筒上端O点以水平初速度v0沿圆筒内壁切线方向抛出.已知重力加速度为g,不计空气阻力.

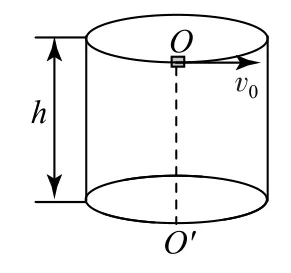
图1

(1)求小滑块从抛出到离开圆筒所用的时间t.

(2)如果沿虚线OO′将圆筒展开,以小滑块初始位置为坐标原点O,初速度v0方向为x轴正方向,竖直向下为y轴正方向,建立直角坐标系xOy,如图2所示.定性画出小滑块在圆筒内表面的运动轨迹.

图2

解析

(1)小滑块在圆筒内的运动可以分解为竖直方向和水平方向的两个分运动.在竖直方向上,小滑块在重力作用下做自由落体运动;在水平方向上,小滑块在圆筒内壁支持力的作用下做速度大小为v0的匀速圆周运动.根据

(2)将圆筒展开,以小滑块初始位置为坐标原点O,初速度v0方向为x轴正方向,竖直向下为y轴正方向,建立直角坐标系xOy.在x轴方向对应的是小滑块沿圆筒切线方向的运动:速度大小为v0的匀速直线运动;在y轴方向对应的是小滑块沿竖直方向的运动:自由落体运动.类比平抛运动,小滑块在圆筒内表面的运动的轨迹为抛物线.设小滑块在水平方向做圆周运动的周期为T.若t＝nT(n为整数,且n≥1),小滑块在圆筒内表面的运动轨迹如图3所示,小滑块从O′离开圆筒.

图3

若(n－1)T＜t＜nT(n为整数,且n≥1),小滑块在圆筒内表面的运动轨迹如图4所示,小滑块从圆筒底边离开(除O′以外),具体离开位置由t决定.

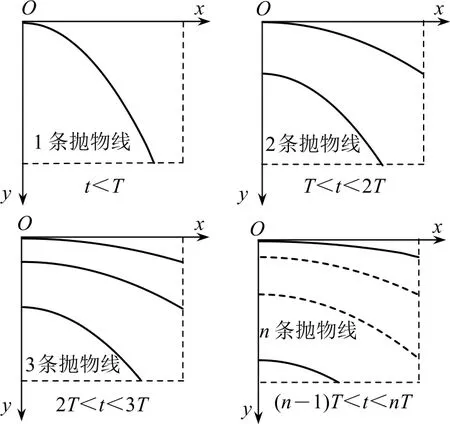
图4

点评

本题情境为重力场中复杂的运动问题,运用“合成与分解”思想将复杂的运动分解为两个熟悉的简单分运动.小滑块从抛出到离开圆筒所用的时间可由小滑块竖直方向的分运动求得,通过分析小滑块竖直方向的受力、加速度和初速度,再运用直线运动规律即可解决该问题.小滑块在圆筒内表面的运动轨迹可以通过研究小滑块竖直方向的分运动和沿圆筒切线方向的分运动获得.

3 复合场中复杂的运动问题

由于电磁场和带电粒子本身看不见、摸不着,对于初学者来说比较抽象,电磁场中的运动问题既是高中物理中的重点也是难点.电荷量为q的带电粒子在电场强度为E的静电场中,所受静电力大小F＝Eq;如果q为正电荷,其受力方向与电场线(切向)方向一致.电荷量为q、速度为v的带电粒子在磁感应强度为B的磁场中,所受洛伦兹力大小F＝Bqvsinθ,方向由左手定则判断.

例2如图5所示,在真空中存在空间范围足够大的、水平向右的匀强电场.将一个质量为m、带正电的小球从电场中某点以初速度v0竖直向上抛出.已知小球所受电场力与重力之比为.求小球从抛出到运动至最高点过程中电势能的变化量ΔEp.

图5

解析

小球从抛出到运动至最高点过程中,小球在竖直方向上只受重力,做竖直上抛运动.设小球从抛出点至最高点运动时间为t,则.小球在水平方向上只受电场力,做初速度为0的匀加速直线运动,加速度.在时间t内,其水平位移为

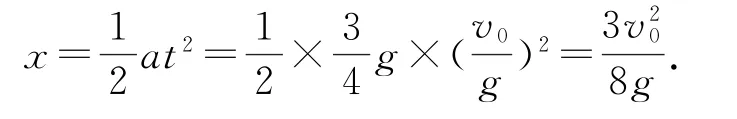
电势能的变化量ΔEp＝－F电x,解得

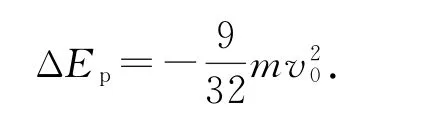
点评

本题情境是带电粒子在复合场(电场和重力场)中做复杂的曲线运动,直接求解困难.运用“合成与分解”思想,将这个复杂的曲线运动分解为两个互相垂直的直线运动,化难为易,问题迎刃而解.

例3如图6所示,在真空中存在空间范围足够大的、水平向右的匀强磁场,磁感应强度大小为B.电子枪(图中未画出)发射出质量为m、电荷量为e的电子,经加速后以初速度v0射入磁场中,初速度方向与磁场方向夹角为θ.不计电子所受重力.求电子在垂直磁感线方向上运动一周的时间内,沿磁感线方向上运动的距离x.

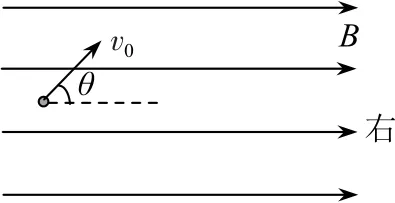
图6

解析

电子的运动可以分解为沿磁场方向和垂直磁场方向两个分运动.在沿磁场方向上电子不受力,以速度v1＝v0cosθ做匀速直线运动;在垂直磁场方向上电子受到指向圆心的洛伦兹力,以速度v2＝v0sinθ做匀速圆周运动.洛伦兹力提供圆周运动的向心力,Bev2＝,周期T＝,电子在T时间内沿磁感线方向运动的距离x＝v1T,解得

点评

本题情境是带电粒子在磁场中运动的一般情况,即带电粒子进入磁场时,速度方向与磁场方向不垂直也不平行,带电粒子(只受洛伦兹力)在磁场中做螺旋线运动.运用“合成与分解”思想将该运动分解为沿磁场方向的匀速直线运动和垂直磁场方向的匀速圆周运动,运用所学相关知识即可解决该问题.

例4如图7所示,空间存在一范围足够大的垂直于xOy平面向里的匀强磁场及沿y轴负方向的匀强电场(电场未画出).一带电粒子在O点由静止释放,并开始计时.已知磁场的磁感应强度大小为B,电场的电场强度大小为E,带电粒子的质量为m,电荷量为q(q＞0),重力不计.求:

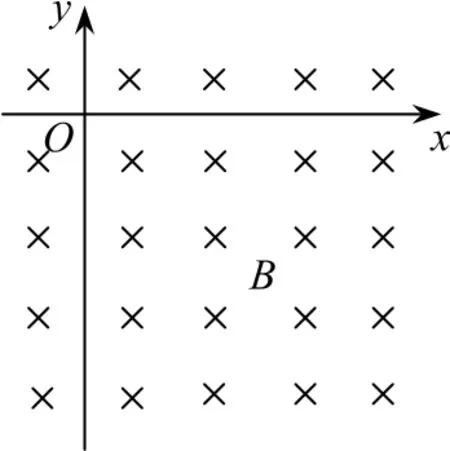
图7

(1)带电粒子在运动过程中的最大速度;

(2)带电粒子在x轴方向的速度vx随时间t的变化关系.

解析

带电粒子由静止释放,初速度可分解为沿x轴正方向的v1和沿x轴负方向的v2(v1＝v2),且v1对应的磁场力与电场力平衡,即Bqv1＝Eq,则v1＝v2＝.带电粒子的运动可以分解为沿x轴正方向、速度大小为v1的匀速直线运动和在xOy平面、速度大小为v2、沿逆时针方向的匀速圆周运动.

图8

点评

本题为复合场(磁场和电场)中复杂的运动问题,解决该问题依然是运用“运动的合成与分解”的方法,将该运动分解为x轴方向和y轴方向的分运动.通过分析分运动方向的受力、加速度和初速度,运用所学相关知识可求得相关物理量.

研究物质的运动是高中物理的重点内容,运动常用位移、速度、加速度等物理量来描述.在处理复杂的运动时,常常利用运动的合成与分解思想将复杂运动分解为几个简单的分运动,通过研究分运动的特征间接研究复杂运动.

(完)