例谈高中物理对称思想在解题中的应用

燕伟

(山东省邹平市第二中学)

对称思想是一种重要的解题思想,尤其在分析物体运动过程、弹簧形变、电场场强等相关物理问题时,运用对称思想能很好地降低解题复杂度,快速确定解题思路,在一定程度上提升学生的物理解题能力.

1 解答上抛类问题

对竖直上抛类问题,既可以逆向考虑,将其看作自由落体运动进行分析,还可根据题干创设的情境运用对称思想把握物体运动的具体规律,化复杂为简单,以顺利构建物理方程,准确、成功解题.

例1将一个物体竖直上抛,其在运动过程中两次经过一个较低的a点的时间间隔为Ta,两次经过一个较高的b点的时间间隔为Tb,则a、b距离为().

2 解答平抛类问题

平抛类问题是高中物理的重要题型.解答该类习题除了要认真理解平抛运动的规律,准确把握平抛运动的特点外,还应具体问题具体分析,注重运用对称思想化零为整,将物体各阶段运动转化成一个整体的运动,确保问题得以顺利解决.

例2如图1 所示,两面光滑的墙面竖直放置在地面上,水平间距为s＝1 m.某时刻在左墙上距离地面高h＝19.6 m的A点,沿水平方向以v0＝5 m·s－1的初速度抛出一个小球.忽略小球和墙面碰撞过程中的能量损失,则小球落地前和墙壁碰撞().

图1

A.8次 B.9次 C.10次 D.11次

分析采用常规思路解题,较为烦琐.考虑到小球与墙面碰撞时能量不损失,表明其碰撞前后小球的速度大小不变,因此可考虑对称思想,将小球运动的整个过程,当作一个完整的平抛运动进行处理.设小球和墙壁碰撞次数为n,运动时间为t,则水平方向上n＝,在竖直方向上h＝,联立两式代入数据解得n＝10次,选项C正确,表明小球刚好落在左墙墙根.

3 解答斜抛运动问题

高中物理学习中,抛体运动问题是难点问题.常见的抛体运动主要有斜抛运动和平抛运动.斜抛运动轨迹关于轨迹最高点所在竖直方向直线对称,因此,在解题中,可利用对称思想有效解答斜抛运动问题.

例3在一个平行板电容器内存在匀强电场E,电场的方向竖直向下,假设一个粒子的质量是m,电荷量是＋q,粒子从A点沿着和水平方向成θ角的方向运动,初速度为v0,如图2所示,最高点是O,H是物体达到的最高高度,h是O1和O2点距离抛出点的高度,物体重力忽略不计,求解物体从O1点运动到O2点需要的时间.

分析结合图2对粒子运动特点进行分析,其运动轨迹关于O点所在垂直平行板方向的直线对称,因此,粒子从O1点到达O点和从O点到达O2点需要的时间是一样的,总时间是以v0cosθ为初速度,从O点到O2点的类平抛运动时间的两倍,由于平抛运动物体在竖直方向做匀变速直线运动,所以,通过计算得

图2

根据解题思路分析,粒子运动是类斜抛运动,在解题中通常按照类平抛运动思路,结合粒子运动的对称特点进行求解.在解题过程中,注重解题思路的变化,利用对称思想将复杂问题进行转换,快速准确解答问题.

4 解答弹簧类问题

弹簧既能够拉伸又能够压缩,其形变具有一定的对称性.解答弹簧类相关的物理习题时,注重运用对称思想能很好地揭示出弹簧的形变规律,迅速找到解题突破口.

例4如图3所示,在竖直光滑杆上套一质量为m的小球.一轻质弹簧一端和小球相连,另一端固定在O点,弹簧和杆处在同一竖直平面内.某时刻从A点释放小球,此时弹簧处于原长.小球下降的最大竖直高度为h时到达B点.OB和杆所成的角为30°,弹簧始终处在弹性限度内,则小球从A运动至B的过程中().

图3

A.弹簧和杆垂直时小球速度最大

B.小球加速度为g的位置有三个

C.弹簧的弹性势能先增大后减小

D.弹簧的弹性势能增加量大于mgh

分析该题目需要明确弹簧的形变过程,借助对称思想进行分析.如图4所示,设弹簧处于水平状态时小球处于C点,D点是A点关于C点的对称点.小球从C点运动至D点的过程中弹簧处于压缩状态,小球加速度大于g,到达D点的加速度为g,因此,弹簧和杆垂直时小球的速度并不是最大的,选项A 错误.小球在A点、C点、D点的加速度均为g,选项B正确.弹簧的弹性势能先增大后减小再增大,选项C错误.系统的机械能守恒,弹簧的弹性势能增加量等于mgh,选项D 错误.

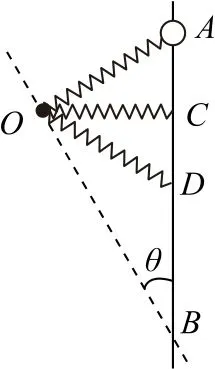
图4

5 解答电场类问题

运用对称思想解答电场问题往往能获得事半功倍的效果.要掌握运用对称思想解答电场类习题的相关思路,应注重相关习题的解题训练,进一步拓展解题视野,锻炼灵活解答物理问题的能力.

例5如图5 所示,一半径为R,圆心为O的均匀带正电的圆环带电荷量为Q.A、B、C是和圆环面垂直且过圆心的轴线上的三点,其中OB＝OA＝BC＝R.将一点电荷放置在C点,忽略其对圆环电荷分布的影响,且整个装置处在真空中.若B点的电场强度刚好为零,则A点的电场强度大小为().

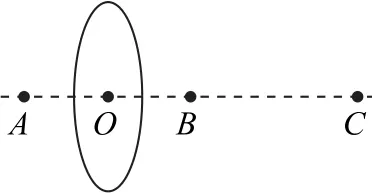
图5

想要掌握对称思想,既要认真做题,又要做好总结,从而在不断犯错、纠错的过程中,逐步提升解题能力.

(完)