一种融合局部拓扑影响力的时序链路预测算法
2022-04-21朱宇航刘树新吉立新何赞园李英乐
朱宇航 刘树新 吉立新 何赞园 李英乐
(中国人民解放军战略支援部队信息工程大学信息技术研究所 郑州 450002)
1 引言
自然界中一切事物都是运动的,现实世界中的各种复杂网络也都是随着时间变化而不停演化的动态网络,如航空交通运输网络、生物网络、文献引用网络、电力网络、社交推荐网络、蛋白质网络等等,这些真实网络都可以抽象成为一个个由节点和连边组成的动态时序复杂网络。挖掘节点与节点之间、连边与连边之间的相互作用,分析动态网络的演化规律,预测网络的变化情况,对研究网络科学和复杂系统具有重要意义。链路预测作为研究复杂科学的重要技术之一,已成为近年来的研究热点问题[1,2]。
链路预测是挖掘网络数据之间潜在关系的一种重要方法,原理就是利用已知的网络节点属性、连边属性和拓扑结构等信息,预测网络中未连接节点之间产生连边的可能性[3]。基于“朋友的朋友很可能也是朋友”等规律,最常用的链路预测指标包括CN(Common Neighbors),AA(Adamic-Adar),RA(Resource Allocation),PA(Preferential Attachment),LP(Local Path),Katz等[4]。近年来,许多学者对预测指标的优化开展了大量的研究工作,李治成等人[5]利用节点的拓扑稳定性对相似性指标进行了优化;王凯等人[6]对信息在传输路径上的有效性进行了刻画,优化了RA指标;刘树新等人[7]从资源传输匹配的角度对资源双向传输进行了准确量化。在静态网络链路预测的基础上,时序链路预测利用每一个时刻的静态预测指标,结合时间序列分析的方法,实现对动态时序网络的分析。最朴素的思路就是对所有时刻图的特征建立总体平均模型[8],即利用每一时刻相似度特征的平均值去预测下一时刻的情况。Huang等人[9]将时间序列应用到链路预测中,计算网络中所有节点对在每一个时刻相似性分数的时间序列矩阵,结果表明,引入时间序列的动态算法性能优于传统的静态算法。Güneş等人[10]将静态网络的拓扑结构相似性指标与ARIMA(Autoregressive Integrated Moving Average model)模型进行融合,提出的时序链路预测算法取得了良好的实验结果。刘继嘉等人[11]利用LR(Liner Regression)线性回归模型对改进相似性特征的时间序列进行建模,实现了对动态网络不错的预测效果。
上述方法从时间序列分析的角度进行分析,未考虑网络演化过程对网络本身的影响,许多学者在计算历史时刻图信息特征的基础上,增加不同的网络演化规律方面的特征,提出了精度更高的时序链路预测算法。如Munasinghe等人[12]认为节点对之间的相互作用会随时间发生变化,如果近期两个节点与它们的共同邻居之间的连边越多,那么未来这两个节点间发生连边的概率也会变大。Zhang等人[13]利用基于隐藏空间模型的方法,把共同邻居的关系映射到隐藏空间,在隐藏空间中的距离越近的节点对,产生连接的可能性更大。邓志宏等人[14]以传统的结构相似性算法为基础,提出了基于误差修正的时序网络链路预测算法,取得了较好的预测结果。Bliss等人[15]通过协方差矩阵自适应演化策略对相似性指标进行了优化,在Twitter数据集中取得较好的精确度。这些时序链路预测算法虽然有效地利用了时间信息,但它们只考虑了局部连边的网络演化规律,对网络拓扑结构的特性挖掘有限。因此,可以进一步挖掘网络微观结构在演化过程中节点变化和连边变化的影响力演化模型。
此外,还有很多学者从网络动力学的角度,对网络的离散性、动态性、自适应和高阶特征等方面开展了相关研究,提出了基于线性方程[16]、基于压缩感知[17]、基于相位同步[18]、基于霍克斯过程[19]等模型,这些模型都把网络演化过程抽象成不同的非线性迭代训练过程,但这些模型要么仅对稀疏连边的演化进行建模,要么仅对连边变化映射相位的演化进行建模,要么仅对节点事件的演化进行建模。这些模型的应用场景比较单一,如线性方程和压缩感知的方法大多把时序网络转换成线性系统,相位同步模型的方法更适应马尔可夫网络,对记忆网络的效果不好,基于霍克斯过程的模型大多针对节点的演化信息进行拟合,而忽略了网络结构的其他信息对网络演化的影响,也没有对各类特征的融合进行建模研究。
基于以上分析,本文首先从研究这些模型的迭代规律入手,认为网络自身的本质特征是网络全局长期的影响效果,把网络拓扑演化过程中节点、连边的自相关和协相关定义为局部影响,再加上噪声的因素,提出一种基于拓扑结构影响力的时序链路预测算法的通用模型 (Common Temporal Link Prediction Model, CTLPM);其次,在仅考虑拓扑局部影响的情况下,利用节点和连边在时序动态网络上的演化规律,给出了融合局部拓扑影响力的时序链路预测算法 (Temporal Link Prediction base on Fusion Local Structure Influence, TLP-FLSI);最后,在7个真实数据集上分步骤进行实验,考察节点和连边作用的权重比例,直接影响力和间接影响力的作用优先顺序,并且与经典时序算法进行预测性能对比,实验结果表明了TLP-FLSI算法的可行性和有效性。
2 问题描述及评价指标
常见的动态网络建模方式是根据时序对数据进行等间隔切分,把动态网络分解为一系列的时间快照图集合,这样的建模方式相当于对动态网络在时间维度上进行采样,将动态网络拆分成多个静态网络序列,使得静态网络的预测算法能够适用于动态网络的处理。
复杂网络通常以图的形式进行描述,静态网络通常用G=(V,E)表示,其中V={v1,v2,...,vN}表示节点集合;N=|V|表示网络中节点数量;E ⊆V×V表示节点集合中任意两个节点连接构成的集合(有向或无向),E={eij|i,j=1,2,...,N},eij表示节点间连接关系紧密度,即边的权重,如果边不存在,eij=0,如果是无权图,则eij始终为1,如果节点对之间是多种关系,则eij可以用向量进行表示。
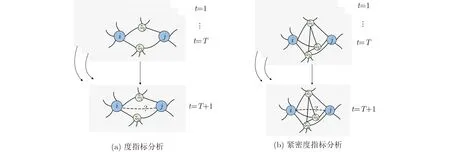
动态时序网络在t (0 时序链路预测是指利用动态网络的历史快照数据G={G1,G2,...,GT},预测GT+1的网络拓扑分布。如图1(b)所示,通过时刻1到时刻T的数据作为训练集合进行建模分析,进而实现对t=T+1时刻的链路预测。 时序链路预测的评价指标与静态链路预测相同,也可以采用AUC(Area Under Curve)指标和RS(Ranking Score)指标[20]对预测结果进行评价。两种指标考虑的着重点不一样,其中,AUC 是最常用的一种评价指标,它能从整体衡量算法的精确度,而RS则更多地考虑了所预测的边的排序。 首先给出时序链路预测通用模型的定义,在此模型基础上提出基于融合局部拓扑影响力的时序链路预测算法,并对节点和连边的历史信息与演化信息进行分析。 网络拓扑的影响力包括全局影响和局部影响,局部影响又可以分为直接影响和间接影响。全局影响力可以衡量拓扑对网络整体的重要性,如中心性指标可用于表示节点和连边的全局重要性,特征向量指标可用于刻画网络产生的长期影响;在网络动态变化时,对于网络中的一个个实体来说,只有与它有关系的节点和连边才会在相邻的一个时刻产生短期影响,节点度指标便可以衡量节点的直接影响力,紧密度指标则可以衡量节点的间接影响力;另外,对时序序列数据进行建模时,还需要考虑噪声和时间衰减变化等因素。因此,发生于T 时刻的新事件不仅受网络的全局和局部拓扑结构的影响,还受之前时刻的历史事件影响。由此,对于时序动态网络的预测,给出预测未来时刻得分矩阵函数的通用模型(CTLPM)为 全局影响力可以使用网络中节点或边的各类中心性指标进行度量。节点的度中心性指标可以更准确地表示它对邻居的影响力,不同网络的节点即使度相同,由于网络整体的最大度不同,它们对邻居节点的影响力也不同;介数中心性利用通过连边的最短路径数量表示该连边和在该连边上节点的重要性,如网络中2个社团之间的连边要比社团之间的连边的重要性更大;特征向量中心性可以表征为节点中心性的函数,与节点连接的邻居越重要,该节点就越重要。不同类型的网络往往具有不同的特色演化规律,可以挑选合适的中心性指标进行度量。 局部影响力可以考虑网络拓扑中节点和连边在局部范围内的结构特征进行融合表示,可以用节点和连边的相似性,以及演化过程中的相关性进行度量。对于t时刻的节点i和j的局部影响力计算为 (1) 首先计算网络中每一个节点的影响力度量、连边的相似性度量以及它们的自相关度量,并分别得到网络的度量矩阵; (2) 使用矩阵的自身数值与矩阵最大数值的比值作为最终的度量得分,如式(7)所示,实现对节点对局部影响力的归一化。其中,V为网络在t时刻的节点集合。 对大规模网络计算全局特征的成本较高,进一步只考虑融合局部拓扑影响力的作用,这样可以大大减低计算的复杂度,给出一种融合局部拓扑影响力的时序链路预测指标,记作TLP-FLSI,具体计算如式(11),它与通用模型的关系如图2所示 图2 TLP-FLSI与CTLPM的关系图 定义FLSI-III为考虑连边和连边协相关因素的 步骤3 计算连边的局部影响力的演化因子,根据连边的1阶和2阶相似度特征,得到连边的局部拓扑影响力得分、连边局部介数的变化比值,并对得分进行归一化; 步骤4 把节点和连边的演化因子按照不同的权重进行求和,得到融合特征的相似度分值; 步骤5 按照时序演化因子,分别按照线性衰减、泊松衰减、指数衰减这3种模型,在时间长度p内,得到该时刻经过时序衰减后的最终相似度分值; 步骤6 返回步骤2,计算下一时刻相似度分值,与之前的总分值进行迭代运算后,得到算法的最终相似度得分值。 下面将分别对节点、连边的局部拓扑影响力的演化因子,以及时间序列分布衰减的演化因子展开进一步的分析。 3.2.1 基于节点局部影响力的演化因子 首先对节点的局部影响力进行分析,如果要预测下一时刻两个节点之间存在连边关系,必要条件是需要保证这两个节点存在,因此,可以认为节点存在的概率越大,连边存在的概率也就越大。链路预测问题可以从节点存在的概率这一角度进行分析,t时刻一个节点对的局部影响力就等于各自节点影响力之和,具体为 根据网络类型的不同,可以从多个角度去定义节点的影响力。一般而言,前一时刻节点存在的连接关系越多,下一时刻节点存在的概率越大,通常利用节点的度指标来表征节点的直接影响力,在社交网络中表示此节点的直接社会关系;利用节点的拓扑紧密性的指标来表征节点的间接影响力,在社交网络中表示此节点的间接社会关系。图3(a)为利用节点度进行影响力演化的示意图,因为只利用目标节点对中两个节点自身的直接影响力进行演化,基于节点度数表征节点对的局部影响力的FLSI-I(1)指标具体为 其中,λ1和λ2分别表示1阶和2阶基于度数的局部作用系数,z表示节点i和节点j的共同邻居。 另外,还可以从节点的拓扑紧密性方面对节点的局部影响力进行设计,如果一个节点对的共同邻居形成的三角闭合关系越多,说明节点对的拓扑越稳定,在下一时刻存在的概率越大。如图3(b)所示,以T 时刻为例,节点i和节点j的共同邻居z1,z2, z3之间的连接关系(z1,z2), (z1,z3), (z2,z3),这3条边都会与节点i和节点j共同形成了三角闭合关系,利用这种三角拓扑的分布情况,基于拓扑紧密度表征节点对的局部影响力的FLSI-I(2)指标具体为 图3 节点局部影响力演化示意图 3.2.2 基于连边局部影响力的演化因子 在静态网络链路预测的方法中,对节点对的连边关系的预测也可以转化为对其拓扑结构中路径信息的相似性判决问题。如LP指标就考虑了有限的3阶路径长度,它的定义为 其中,A表示网络的邻接矩阵,λ为调节参数,S是最终的得分预测矩阵。而Katz指标把节点i和节点j之间的全局所有路径都考虑进来,定义为 该思路利用了真实路径和虚拟路径对资源分配的共同作用,那么在动态网络中对路径的影响力进行综合考虑,可以把动态网络在每一时刻的路径影响都进行计算。如图4所示,不仅要考虑节点i和j之间的连边变化情况,还要考虑它们与共同邻居之间连边的变化情况。 图4 连边局部影响力演化示意图 无向网络连边的1阶相似性是指有连边存在的节点对之间的相似性[22],主要由连边的权重决定,没有连边的节点对之间的相似性为0,2阶相似性是指节点的邻近网络结构的相似性,若节点间没有共同的1阶邻居,则2阶相似性为0。针对动态网络的某一时刻t,考虑1阶路径和2阶路径的结构作用,基于连边局部影响力的FLSI-II指标具体为 在连边局部影响的基础上,考虑连边的自相关演化因素为相邻时刻连边的局部介数的比值,连边的协相关演化因素为在不同时刻的虚拟2阶路径,得到FLSI-III指标具体定义为 3.2.3 基于时序衰减的影响力演化因子 网络拓扑的节点和连边可以抽象成一个个事件,这些事件可以组成时间序列数据。时间序列的模型一般可以分为加法模型、乘法模型和混合模型。对应这3种模型,可以拟合成线性分布、长尾分布、钟摆分布这3种概率分布模型,如图5所示。 图5 影响力时序演化示意图 假设拓扑影响力按照线性分布进行演化,事件的影响力随时间变化按照固定大小进行线性衰减。 假设拓扑影响力按照长尾分布进行演化,事件的影响力随时间变化按照先急剧下降,再缓慢下降的模型进行衰减,本文用指数衰减来拟合长尾分布的时序演化场景。 假设拓扑影响力按照钟摆分布进行演化,很多热点事件影响力衰减的情景是符合钟摆分布模型,事件发生后影响力在均值时间前是上升的,之后再进行下降的衰减。本文用泊松变化来拟合钟摆分布的时序演化场景。 本文采用7个通信社交网络数据集对算法性能进行评估。Email数据集[23]是某大型欧洲研究机构从2003年10月到2005年5月的电子邮件数据生成的;Enron数据集[24]由Enron公司从2001年1月到2002年3月雇员之间发送的电子邮件数据组成;Facebook数据集[25]包含了从2006年11月到2009年1月用户在另一个用户墙上留言的交流记录;DNC数据集[26]由2016年5月美国民主党全国委员会邮件泄露事件中采集的邮件往来网络,其节点表示邮件账号,连边表示某账号发往另一账号的邮件;MAN数据集[26]是某制造业工厂内部员工的邮件往来网络,包括2010年1月至10月的邮件数据;UCI数据集[27]由加州大学欧文分校的学生之间传递的短信构成的在线社交网络,选用2014年7月至11月的连边构建数据集;LEM数据集[28]由堪萨斯事件数据系统基于包含WEIS编码事件的文件夹收集的交互网络,涵盖了1979年4月至2004年6月内的事件,各数据集参数如表1所示。 表1 数据集参数表 (1)基于最近时刻算法[8]:利用马尔可夫网络的思想,假设每一个时刻仅与最近的一个相邻时刻有关,只使用网络最近一个时刻的相似度指标进行预测的方法,记作Last。 (2)移动平均时序算法[10]:利用移动范围内每一个训练时间快照的相似性指标的均值进行度量的方法,记作AV,如果移动范围为预测之前的全部窗口,则算法等价为总体平均算法,如果移动范围仅为预测之前的1个窗口,则算法等价为最近时刻算法。 (3)基于邻居扩展指标的时序链路预测算法[10]:基于邻居扩展指标的方法对时序网络数据进行分段加权处理的同时,基于距离越近,作用越大的原理,再结合指数函数表征时间的衰减作用,记作TS-W。 (4)基于有效增量的时序链路预测算法[13]:该方法仅对时序网络中的节点增量和增量节点对应的邻居重新计算影响力得分,由于只考虑了2阶条件下的节点增量更新处理,使得减小了计算复杂度的同时,也能获取不错的检测精度,记作TLP-I。 (5)基于误差修正的时序链路预测算法[14]:将每一个时刻的预测分值与连接关系之差为预测误差,再计算相邻时刻的误差的偏移,进而融合得到最终的误差预估矩阵,把最后一刻的预测进行最终误差修正后得到预测得分,记作LPE。 (6)基于概略图的算法[29]:把移动范围内所有时刻快照图叠加成为一个有权静态图的方法,记作Reduce。该方法把有权静态图当作最近邻时刻图进行训练,实现对下一时刻的预测。 (7)基于节点匹配度的时序链路预测算法[30]:该方法在两级拓扑结构中,利用节点三角形闭合数量和节点度共同定义节点的重要性,利用指数衰减对时序作用进行拟合,记作TMDN。 (8)基于自注意力机制实现的图嵌入模型算法[31]:利用网络拓扑自注意力聚合网络快照中各节点的结构特征,利用多头注意力机制捕捉网络快照之间的演化特性,记作DySAT。 (9)基于图注意力网络的动态链路预测方法[32]:利用图注意力网络提取静态网络快照中的结构特征,随后利用门控循环单元提取网络快照序列中的时序演化特征,并结合自注意力机制聚焦重要的网络快照,利用生成的图嵌入向量实现对未来连边可能性的评估,记作TASM。 4.3.1 性能对比分析 实验初始设置如下:设定训练时长p=7,即固定利用预测时刻的前7个时刻的网络数据进行训练;设定λ1=λ2=1,即考虑节点和连边的1阶影响和2阶影响相同;设定线性时序衰减d=1/7;指数时序衰减因子d=0.8,则指数的时序衰减为(0.8)T −t,t为距离T 时刻的时间间隔数量;设定泊松时序分布的均值为2。 对本文提出的FLSI-I, FLSI-II和FLSI-III算法,首先计算节点和连边的局部影响力演化因子后,再进行线性、指数、泊松时序衰减变化,其中,FLSI-I(1)采用节点度数计算节点的局部影响力,FLSI-I(2)采用节点的集聚系数计算节点的局部影响力。Last,AV, Reduce, LPE, TS-W, TLP-I, TMDN这7种模型分别使用CN, AA, RA, JC等几种相似性指标进行的时序模型运算,以及对比DySAT, TASM这2种基于图注意力网络的方法,并且对连续多个时刻进行预测取得平均值后,对它们的AUC值进行对比,实验结果如表2所示。 表2 不同方法的平均AUC性能结果 首先对比FLSI方法与其他方法,在Facebook数据集中FLSI方法比DySAT和TASM的效果差,但是对比7种基于结构相似性的时序方法仍然取得了相对较好的效果;在其他6个数据集中FLSI都取得了更好的预测效果,3类FLSI方法的效果比其他模型的AUC性能有明显提升,平均提升的幅度在1%~8%。 然后对比3类FLSI方法的效果,总体上看,在几个网络数据集中,其中FLSI-II的效果最好。对比基于节点度的FLSI-I(1)方法比基于节点紧密度的FLSI-I(2)方法,在Email, DNC和LEM这3个数据集中效果相差不大,说明在前5个数据集中的节点直接影响力和节点的间接影响力的作用差不多,在Enron, Facebook和UCI网络中FLSI-I(2)的效果不好,说明这时节点的直接影响力比间接影响力的作用大很多,在MAN数据集中则正好相反;除了MAN数据集,在其他6个数据集中FLSI-II和FLSI-III方法的效果优于FLSI-I方法,说明在这几个数据集中利用连边信息比节点信息的效果更好;FLSI-III比FLSI-II效果稍差一点,说明基于连边的相关性因素虽然产生了一定的影响力,但由于与连边的局部拓扑影响计算出现了一定的重复,所以产生了一些负面的作用。 对于RS评价标准来说,越低的RS值意味着链路预测方法对准确边的排序越靠前,则表示预测性能越好。从图6所示结果可以看出,与AUC结果相似,在大多数网络中FLSI-II和FLSI-III指标的RS值相比其他方法取得了更好的效果;同时,除了FLSI-I(2)在Facebook和UCI数据集中的效果不好之外,FLSI-I的2种方法RS性能也比其他方法好。FLSI方法的平均RS性能在几个数据集中提升幅度在1.5%~20%。 图6 不同方法的平均RS性能对比图 综上所述,在AUC和RS衡量标准下,本文提出的TLP-FLSI方法的时序链路预测效果优于采用移动均值、误差修正或加权演化的基于结构相似性预测算法效果,预测性能提升幅度显著,实验效果最好的是利用连边影响的FLSI-II模型。FLSI模型较好地利用了网络的拓扑结构的历史信息和网络的动态演化信息,实现了更高的预测效果。在Facebook数据集中基于图嵌入学习的2种预测方法效果最好,但对资源消耗有要求的复杂网络分析场景时,FLSI方法具有更好的应用价值。 4.3.2 参数敏感性分析 由于FLSI-III的精度比FLSI-II的AUC效果稍差,在对局部影响力的调节系数进行敏感性测试时设置β=1−α, δ=0,观察在只考虑节点和连边对局部影响力发挥作用时,1阶特征和2阶特征对最终准确率的影响情况,观察在7个数据集的实验结果变化曲线,利用节点度与连边影响力不同比例的变化记作KE方法,利用节点集聚系数与连边影响力不同比例的变化记作CE方法;在α=1时,KE即是FLSI-I(1)方法,CE即是FLSI-I(2)方法。 步骤1 考虑直接影响力和间接影响力产生相同作用的情况,设置节点和连边的1阶和2阶局部作用系数分别为λ1=λ2=1,在数据集中测试不同的权重参数α的比例,验证对最终相似性得分的影响。实验选取30次不同时刻的AUC平均值作为最终的结果进行对比,如图7(a)—图7(g)所示,从结果可以看出不同的权重值对AUC的影响,观察到随着权重参数的变化,AUC的值也在波动变化。在Email和MAN这2个数据集中,KE方法显示上升波动,CE方法显示下降波动,说明节点或连边在不同场景下需要配置不同的比例,才能取得最好的效果;在Enron, Facebook, DNC和UCI中KE和CE方法的效果波动不大,只有CE方法在α=1时发生陡变,调节系数设置不大于0.9就可以得到较好的AUC值;在LEM数据集中,KE和CE方法的AUC结果随着α的变化而波动,最优的调节系数介于0和1之间,说明节点和连边特征融合后共同对最终的AUC计算产生影响。 图7 步骤1实验权重参数影响的变化曲线 步骤2 设置连边的局部作用系数分别为λ1=0,λ2=1,节点的局部作用系数仍为λ1=λ2=1时,此时连边只有2阶间接影响,实验结果如图8(a)—图8(g)所示,在前5个数据集中都在α=0.1时精度产生了大幅提升,说明了节点产生的影响非常重要,此时,KE曲线比CE曲线得到的AUC得分更高,因为集聚系数表示邻居节点的聚集程序,在网络拓扑中距离需要预测的连边更远,说明在这5个真实社交网络数据集中,节点的直接影响力比间接影响力要大,而在后2个数据集中则得到相反结论。 图8 步骤2实验权重参数影响的变化曲线 步骤3 设置节点和连边都不考虑1阶影响力的情况,即设置局部作用系数都为λ1=0,λ2=1,如图9(a)—图9(g)所示,可以看到在7个数据集中调节参数在不同位置时取得相应的最优AUC值,说明2阶情况下,仍是节点和连边特征融合共同作用能够取得最优值;同时,不考虑1阶特征的情况下,AUC整体比前面2种情况要低,说明节点和连边的1阶特征具有重要的影响作用。 图9 步骤3实验权重参数影响的变化曲线 综上所述,在采用FLSI方法针对通信社交类动态网络进行时序预测分析时,距离待预测连边的距离越近,拓扑实体所产生的影响力越大。连边的1阶信息表示待预测连边在过去时刻的存在情况,可以看成与待预测连边的距离为0;待预测连边的两侧节点的距离次之,它们的影响力仅次于1阶连边;以此类推,与共同邻居连边的影响力再次之,然后才是共同邻居节点的影响力。在FLSI模型和通用时序链路预测模型中,都需要针对这种规律调节局部作用系数的大小;在不同的局部作用系数下,考虑节点和连边的权重调节参数,即如果网络连边的拓扑情况较好,则连边的权重应该分配更大,反之,则节点的权重应该分配更大。 本文总结了基于时间序列分析和基于连边动态演化的时序链路预测方法,提出了一种基于拓扑结构影响力的时序链路预测算法的通用模型。在不考虑噪声和全局特征的前提下,仅利用节点和连边局部拓扑特征影响力演化的规律,给出了基于融合局部拓扑影响力的时序链路算法TLP-FLSI。在7个真实社交网络数据集上的实验结果表明,该算法具有较好的预测效果。本文实验中,只对局部拓扑特征的调节系数做了敏感性测试,后续研究中将针对更多其他类型的时序网络,对模型的衰减调节参数、训练窗口的时间长度、数据集划分间隔长度等参数进一步分析,以及针对时序的网络全局特征和网络环境噪声的影响展开分析,进一步提高该时序链路预测算法的普适性。

3 算法设计
3.1 基于网络拓扑影响力的通用时序链路预测模型



3.2 融合局部拓扑影响力的时序链路预测算法




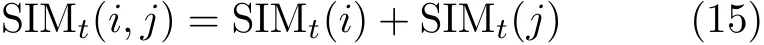
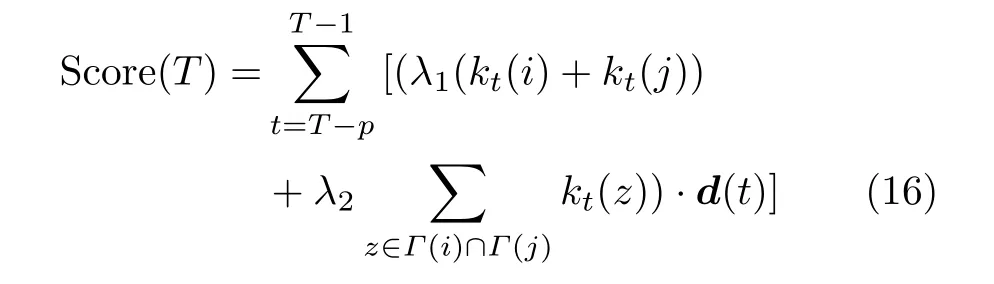







4 实验验证
4.1 实验数据集

4.2 实验对比算法
4.3 实验结果分析






5 结束语
