基于快速后向投影的超宽带冰雷达数据成像算法

稂时楠 许 奔② 崔祥斌

①(北京工业大学 北京 100124)

②(中国极地研究中心 上海 200136)

1 引言

南极冰盖是地球上最大的大陆冰盖，其质量平衡和稳定性对海平面上升有着重要的影响，因此需要大范围地获得冰盖的高分辨率信息[1–3]。超宽带(Ultra-WideBand, UWB)雷达拥有优良的穿透性能和距离向分辨率，在南极冰盖数据信息获取中得到了广泛的应用[4–7]。

合成孔径雷达(Synthetic Aperture Radar, SAR)成像技术多年来一直应用于冰雷达探测数据[8,9]，以提高信号增益和成像分辨率[10]，其主要分为两大类：基于快速傅里叶变换 (Fast Fourier Transform,FFT) 的算法和基于后向投影的算法[11]。最早实现的SAR方法是匹配滤波方法，即将参考点目标的回波响应与来自格陵兰冰盖的雷达数据进行相关处理[8,12]，该方法最近被应用于处理来自西南极的冰盖数据[13]。f-k徙动算法，这是基于反演雷达回波到其在冰中的目标源的算法，该方法也已应用于处理来自格陵兰和南极的数据[14,15]。最近，Lang等人[16]提出了一种方法，利用基于逆尺度傅里叶变换 (Inverse Scaled Fourier Transform, ISFT) 的改进距离徙动算法来抑制方位向杂波，利用曲波波束形成来抑制跨航迹向杂波。此外，Lang等人[17]开发了一种使用曲波的改进距离徙动算法，该算法比fk徙动算法更有效，可以在不降低方位向杂波抑制能力的情况下减少成像过程中的斑噪声。Lang等人[18]还提出了一种基于ISFT的改进平面子阵处理算法，成功实现了冰盖地形的实时成像，在不降低方位向分辨率的情况下，明显降低了冰雷达探测数据实时成像的计算负担。上述方法均在方位向频域内进行处理。这些基于FFT的算法速度快，但由于它们是针对线性孔径推导而来的，因此不容易推广到常见的非线性情况。这意味着如果冰雷达平台明显偏离直线，数据的运动补偿就会出现问题[15]。同时。在基于后向投影的算法方面，Kusk和Dall[19]将时域后向投影方法应用于冰雷达数据。该方法可以处理非均匀采样数据，但计算时间较长。Wu等人[20]采用多子孔径时域后向投影算法进行成像，提供了冰盖表面和基岩的精确条带成像。该方法利用子孔径可以提高处理效率，但会影响成像的方位向分辨率。因此我们的目标是寻找一种快速的方法来处理超宽带冰雷达数据，在保证高成像分辨率的同时，具有基于FFT算法的效率。

Yegulalp[11]提出了一种方位向时域SAR成像算法，称为快速后向投影 (Fast Back-Projection,FBP) 算法，其效率与基于FFT的算法相同。但该方法并不适用于冰雷达数据的多层媒质情况，需要通过对算法进行一些有效的改进来实现对冰雷达数据的处理。

本文提出一种基于快速后向投影的超宽带冰雷达成像算法，利用快速后向投影实现高分辨率的冰层探测数据的高效成像。本算法将传统的FBP算法[11]进行了改进，修正了雷达与目标之间的距离，并根据多层媒质折射现象，对因其造成的距离徙动的几何变化进行了修正，使其适用于超宽带冰雷达数据的多层媒质成像情况。与匹配滤波方法[8]相比，匹配滤波等基于方位向FFT的算法是针对线性孔径的，不容易扩展到常见的非线性情况，雷达平台可能会出现高度和方位的变化，并可能经历翻转俯仰和偏航等明显偏离直线的运动，导致数据的运动补偿会出现问题[20]。而本文算法直接在时域对数据进行处理，可以在时域更直接地处理雷达平台运动带来的误差。与冰雷达直接后向投影算法[19]相比，该算法使用了快速后向投影技术，极大地减少了计算量，在不降低方位向分辨率的情况下极大地提升了计算效率。与多子孔径时域后向投影算法[20]相比，本算法在利用子孔径处理后将子图像数据融合至高分辨率图像，极大提升了图像的方位向分辨率。

本文的其余部分组织如下。第2节对所提算法的理论分析和应用步骤进行了概述。第3节通过将算法得到的成像结果与现有常用冰雷达成像算法的成像结果进行对比，来验证算法的有效性。结论载于第4节。

2 成像算法

基于快速后向投影的超宽带冰雷达成像算法将传统的快速后向投影算法推广到了多层媒质，其拥有高分辨率成像效果和高杂波抑制能力以及与频域算法相当的成像效率。

由于雷达在不同媒质中的传播速度不同，以及信号的传导会因媒质的改变发生折射现象，导致冰层中的距离徙动会发生明显几何变化，因此目前已有的FBP算法[11]并不能直接应用于冰雷达数据的多层媒质的情况。对此，本文修正了位于冰下基岩与空气-冰界面之间的目标的实际高程[19]，即雷达与点目标之间的距离可以表示为

其为空气中的距离Rair(τi,ηj)与冰层中的距离Rice(τi,ηj)之和，其中nice是冰川中冰的折射率[21]。同时，本文结合多层媒质折射现象，对距离徙动的几何变化进行了修正，几何关系如图1所示。

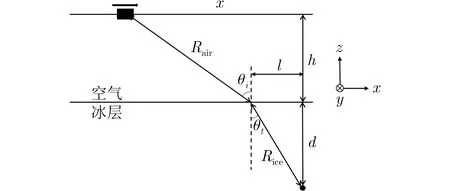
图1 空气-冰层多层媒质的几何关系示意图

接收到的信号经过下变频和低通滤波后，再经过匹配滤波，完成了距离向脉冲压缩，处理后信号可表示为[22]

为了提高分辨率以及抑制杂波，本文提出基于快速后向投影的超宽带冰雷达成像算法，将时域快速后向投影算法[7]改进并应用于超宽带冰雷达数据的SAR成像。快速后向投影算法可以分为两个步骤：子图像处理、最终图像处理。原始数据的像素点序列如图2(a)所示，其中红点为子图像中心列，经过子图像处理得到的像素点序列如图2(b)所示的较为稀疏的子图像序列，最后经过最终图像处理将子图像融合得到如图2(a)所示的高分辨率图像。

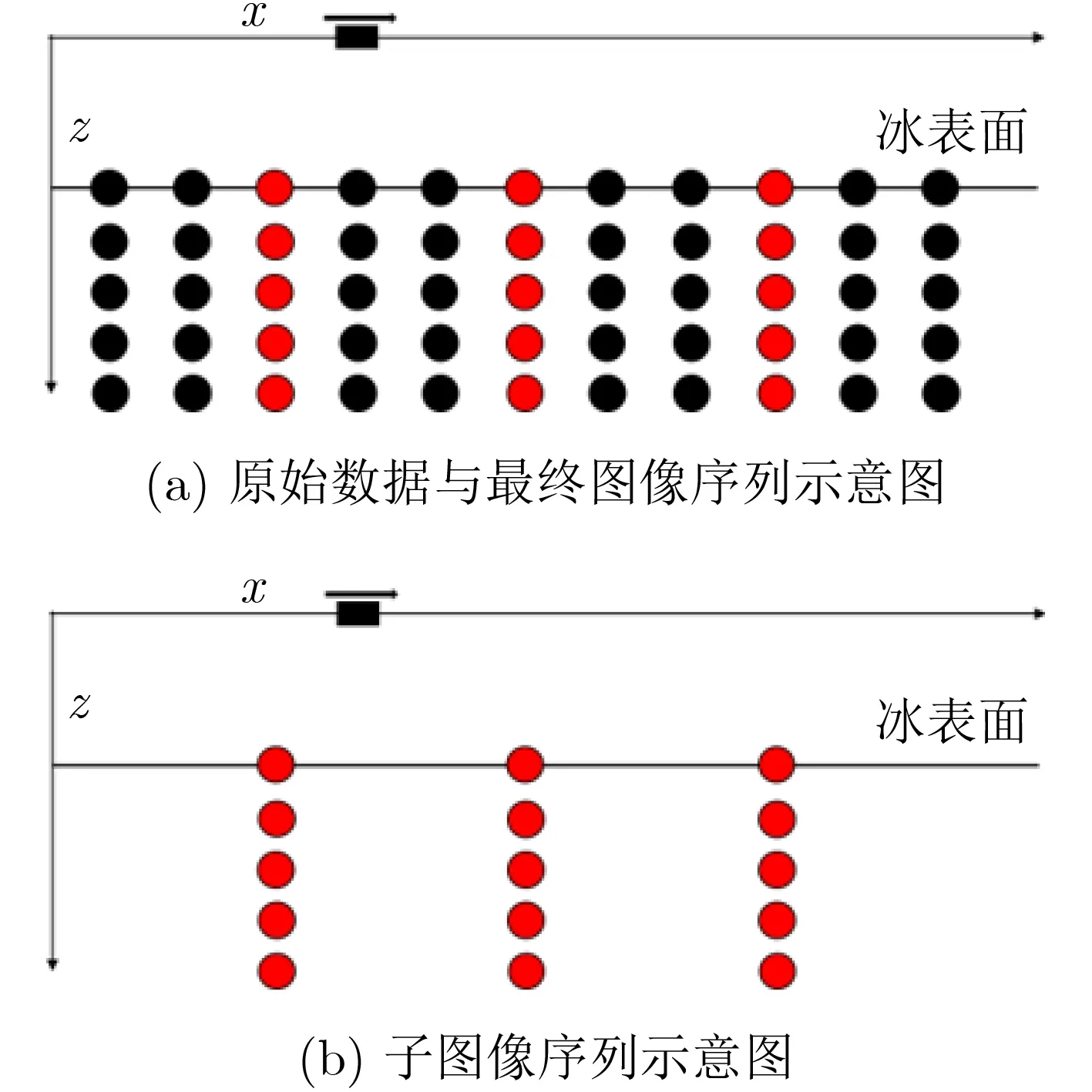
图2 原始数据与最终图像以及子图像序列的关系示意图

本文所提方法的具体步骤如下：

首先，利用傅里叶变换的特性，通过对频谱进行补零对经过距离压缩的数据距离向进行过采样。随后，利用传统的后向投影方法，对子孔径内经过过采样的数据块进行处理，得到子图像的序列。计算过程表示为

因此，基于快速后向投影的超宽带冰雷达成像算法包含以下步骤。

(1)对接收信号数据进行距离匹配滤波以完成脉冲压缩。

(2)利用傅里叶变换特性对信号频谱进行补零，以在距离向上对经过脉冲压缩的数据进行过采样。

(3)利用传统后向投影算法，对过采样数据进行处理得到子图像序列。

(4)利用前一步得到的一系列子图像获得高分辨率图像。

(5)对高分辨率图像进行非相干叠加获得最终的高分辨率图像。

基于快速后向投影的超宽带冰雷达成像算法流程图如图3所示。

3 仿真与实验结果

3.1 仿真结果

仿真和实验结果验证了所提基于快速后向投影的超宽带冰雷达成像算法的有效性。所有点目标仿真与实验处理过程都在同一Windows 10系统联想电脑的Matlab(R2020b)上并行运行，CPU为Intel(R) Core(TM) i7-9750H，CPU频率为2.60 GHz，内存为64 GB。

仿真结果包括两个部分，第1部分对5个点目标进行了仿真，3个点目标具有相同的双向回波时间，其中1个点目标放在冰层中的最低点，两个点目标沿方位向放置在冰面上，其余的两个点目标沿最低点目标等间距放置，如图4(a)所示。最低点目标坐标位于(0,2000 m)，等间隔长度为500 m。第2部分对3个点目标进行了仿真，3个点目标均与第1部分一致，沿方位向放置在冰面上的两个点目标被移除了，如图4(b)所示。仿真参数见表Ⅰ。为了更详细地分析成像情况，对图4的最低点目标进行了分析，结果如图5所示。从图5(a)可以看出，两个最低点目标的功率近乎相等，说明冰面上的两个点目标受到了抑制。从图5(b)和图5(c)可以看到图3(b)最低点目标的脉冲响应。距离向分辨率的计算表示为[23]

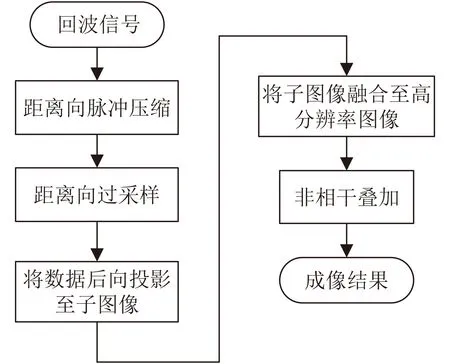
图3 基于快速后向投影的超宽带冰雷达成像算法流程图

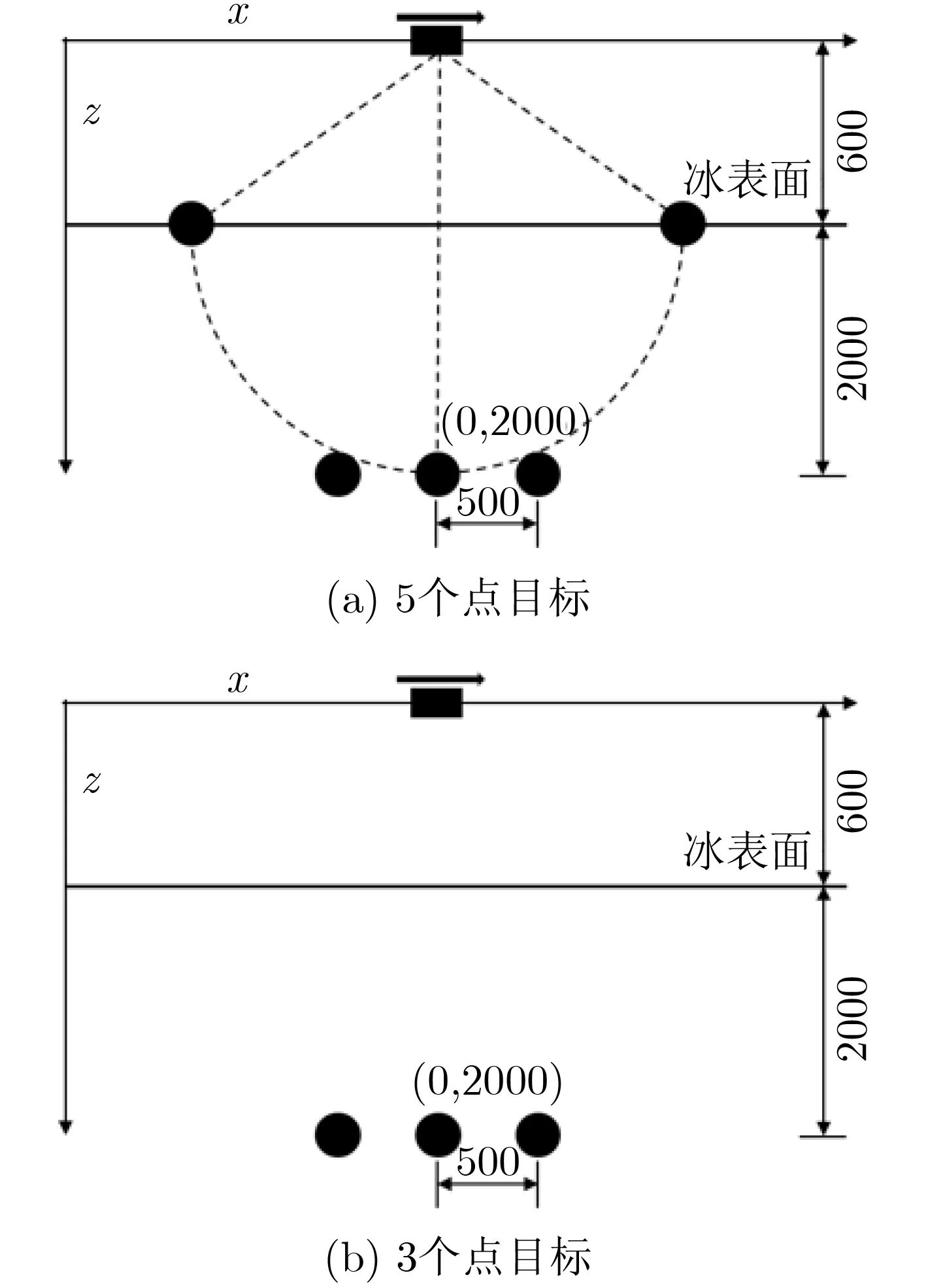
图4 仿真中使用的点目标位置

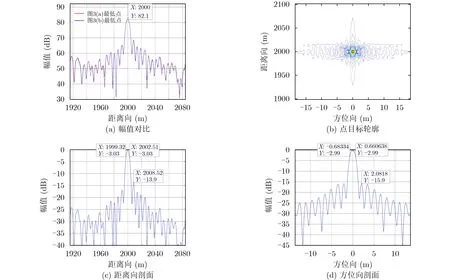
图5 点目标分析

根据表1的仿真参数，通过式(5)计算得到的距离向理论分辨率为4.97 m，测量3 dB宽度得到的距离向分辨率为5.19 m，距离向峰值旁瓣比为–13.9 dB，通过式(6)计算得到的方位向理论分辨率为1.08 m，测量3 dB宽度得到的方位向分辨率如表2所示，为1.34 m，其计算时间为2195.04 s，方位向的峰值旁瓣比为–15.9 dB，点目标仿真结果与理论值一致。

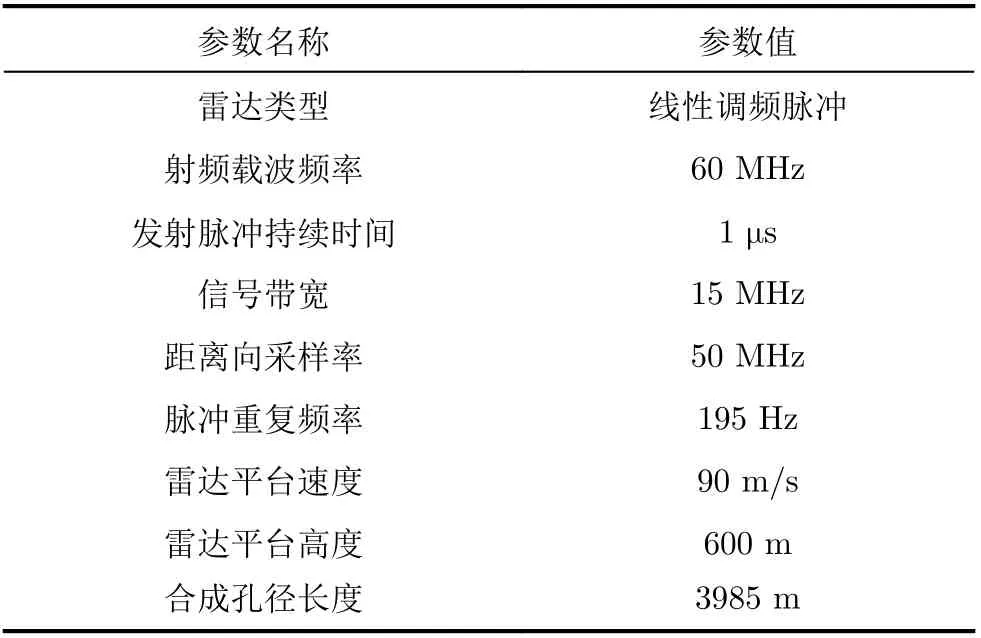
表1 仿真参数

同时，本文使用了多子孔径时域后向投影算法[20]，冰雷达直接后向投影算法[19]以及匹配滤波算法[8]对图4的最低点目标进行了仿真，结果如图6(a)—图6(c)所示，各算法结果测量得到的参数如表2所示。

表2 点目标处理测量结果

由图6(a)可以看到，多子孔径时域后向投影算法结果测量3 dB宽度得到的方位向分辨率为84.96 m。由图7可以看到，其最低点目标的功率与无方位向表面杂波的功率近乎相等，说明冰面上的杂波受到了抑制。其计算时间为2080.20 s，方位向的峰值旁瓣比为–16.7 dB。

由图6(b)可以看到，冰雷达直接后向投影算法结果测量3 dB宽度得到的方位向分辨率为1.22 m。由图7可以看到，其最低点目标的功率与无方位向表面杂波的功率近乎相等，说明冰面上的杂波受到了抑制。其计算时间为12464.34 s，方位向的峰值旁瓣比为–12.6 dB。

由图6(c)可以看到，匹配滤波算法结果测量3 dB宽度得到的方位向分辨率为1.22 m。由图7可以看到，由于点目标仿真为理想的线性孔径，其结果与冰雷达直接后向投影算法结果几乎完全重合，其最低点目标的功率与无方位向表面杂波的功率近乎相等，说明冰面上的杂波受到了抑制。其计算时间为1727.86 s，方位向的峰值旁瓣比为–12.6 dB。

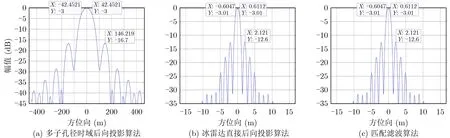
图6 点目标方位向剖面图

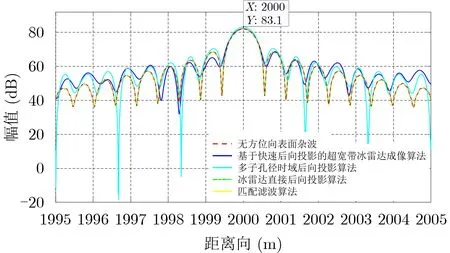
图7 点目标距离向对比剖面图

因此，本文方法与多子孔径时域后向投影算法有基本相同的计算效率，且与冰雷达直接后向投影算法有基本相同的成像分辨率。

3.2 实验结果

本节以中国第33次南极科学考察期间收集的超宽带冰雷达数据[25]，说明了所提基于快速后向投影的超宽带冰雷达成像算法的准确性。关键参数在图中给出[1]。图8所示为中国第33次南极科学考察期间从T1(79°35′41″S, 79°29′01″E)到T1′(71°56′06″S,79°52′60″E)和T2(79°35′41″S, 79°29′01″E)到T2′(71°56′06″S, 79°52′60″E)在东南极冰盖上获得的超宽带冰雷达数据。

图8 实验中处理的测线位置

经过本文所提算法处理后的雷达剖面图如图9(a)和图10(a)所示。此外，本文将该算法与多子孔径时域后向投影算法[20]和冰雷达直接后向投影算法[19]成像结果进行了比较，证明了该算法在方位向杂波抑制和计算时间方面的优势。多子孔径时域后向投影算法成像结果与冰雷达直接后向投影算法成像结果如图9(b)、图9(c)和图10(b)、图10(c)所示。从方位向杂波抑制能力、计算时间两个方面进行了比较。

一方面，本文将所提算法与多子孔径时域后向投影算法进行了比较。图11(a)和图11(b)的红色曲线为所提算法，黄色曲线为多子孔径时域后向投影算法。这些曲线基本呈现出一致的趋势，这意味着多子孔径时域后向投影算法与本算法的方位向杂波抑制能力基本相同。图9(a)和图9(b)的计算时间分别为2625 s和2570 s，而图10(a)和图10(b)的计算时间分别为3675 s和3570 s。计算时间对比表明，多子孔径时域后向投影算法的成像效率与本文算法的成像效率基本一致。

另一方面，本文将所提算法与冰雷达直接后向投影算法进行了比较。图11(a)和图11(b)的绿色曲线表示冰雷达直接后向投影算法。对比绿曲线和红曲线，可以看出冰雷达直接后向投影算法方位向杂波的抑制能力与本文算法基本相同。图9(a)和图9(c)的计算时间分别为2625 s和11409 s，而图10(a)和图10(c)的计算时间分别为3675 s和15962 s。计算时间对比表明，该算法可以明显减少超宽带冰雷达数据成像所需的计算量。

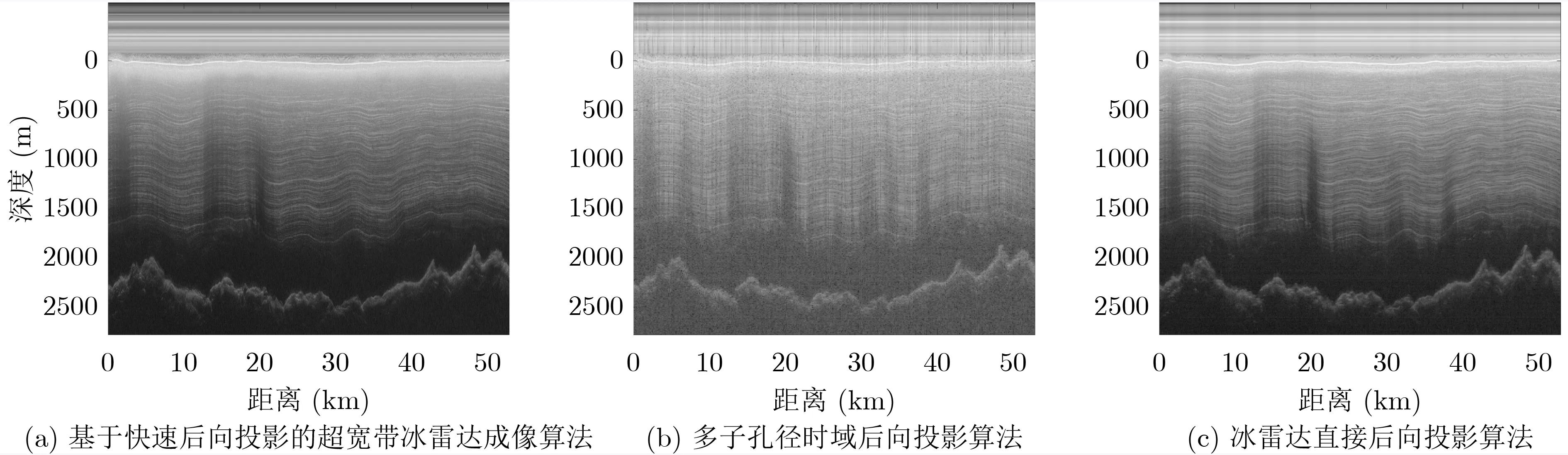
图9 测线T1T1′的各算法的实验结果

图10 测线T2T2′的各算法的实验结果

图11 单道对比结果

通过前面对方位向杂波抑制能力、计算时间和成像分辨率的比较，可以得出结论：基于快速后向投影的超宽带冰雷达成像算法在不降低方位向杂波抑制能力的前提下，提高了超宽带冰雷达数据处理的效率，并且拥有和冰雷达直接后向投影算法相同的成像分辨率。

4 结束语

本文提出一种基于快速后向投影的超宽带冰雷达成像算法。通过点目标仿真与真实冰雷达数据成像对比，验证了该算法在提升计算效率、抑制杂波方面以及高成像分辨率的能力，本算法能够在不降低方位向杂波抑制能力和分辨率的前提下，提高了计算效率。本算法在实际应用中具有一定的灵活性，可应用于机载超宽带冰雷达所采集数据，通过适当的运动补偿方法可以更好地降低方位向表面杂波。