基于GAM 模型和随机森林车险索赔次数预测

□文/孙 静

（南京信息工程大学 江苏·南京）

［提要］ 近年来，广义可加模型（GAM）在非寿险中得到广泛的应用，随机森林作为极具代表性的一种集成学习方法在非寿险领域也取得很好的效果，为非寿险产品定价提供了一种新的选择。因此，本文针对一组具有零膨胀特征的索赔次数数据，建立零膨胀泊松分布和零膨胀负二项分布下的GAM 模型，并将其与随机森林模型进行比较分析。结果表明：预测效果最优的是基于零膨胀泊松分布的GAM 模型。在此基础上，对各解释变量进行分析，为车险费率的厘定提供一定的参考。

在对车险的研究中，车险费率占据着举足轻重的地位，因此保险公司必须建立适合的定价模型来厘定更为合理的费率。一般来说，车险费率模型主要分为索赔频率模型和索赔强度模型，本文仅考虑索赔次数的预测模型。由于实际中的索赔次数通常具有零膨胀性质，故Yip和 Yau（2005）引入零膨胀模型，并分别用 ZIP、ZINB、ZIGP、ZIDP 回归模型拟合车险索赔次数，结果表明零膨胀模型可以改善对数据的拟合效果。广义线性模型（GLM）作为车险费率厘定中最常用的模型，却不能有效地处理非线性问题，故Hastie 等（1986）提出广义可加模型（GAM），可以将连续型解释变量以平滑函数形式引入回归模型，改善模型的预测精度。关于GAM 模型的应用，Günther 等（2014）利用广义可加模型预测客户离开保险公司的风险概率，发现广义可加模型能很好地识别解释变量之间的非线性关系。张连增和申晴（2019）使用广义可加模型对交强险索赔频率建模，并对索赔频率影响因素进行分析。

随着信息技术的迅速发展，机器学习成为统计领域的热门工具。在车险费率研究中，Guelman（2012）使用梯度提升树对索赔频率和索赔强度进行预测，结果显示该模型的预测效果比GLM 模型的效果要好。孟生旺（2012）对索赔频率的线性回归模型、广义线性模型、神经网络、回归树进行比较，发现神经网络的预测效果优于各种广义线性模型，而回归树仅优于线性回归模型。Lee 和Antonio（2015）对索赔频率分别建立GLM 模型、GAM 模型、神经网络和决策树，通过比较发现神经网络的预测效果最佳。Wüthrich 和Buser（2017）对机器学习诸多算法的基本原理进行简要梳理，并分别介绍这些算法在非寿险定价中的简单应用。Noll 等（2018）用GLM 模型、回归树、提升算法和神经网络等对索赔频率进行建模分析，并比较几个模型在建模中的表现。张连增和谢厚谊（2018）使用泊松回归树和bagging 方法对车险索赔频率进行预测，研究结果表明回归树的效果不如广义线性模型，而bagging 法可以提高回归树的预测能力。曾宇哲等（2019）用多种机器学习方法和GLM 模型对7 个数据集进行拟合，结果显示在所有数据集上XGboost的预测效果均优于GLM 模型。

本文选用随机森林和基于零膨胀泊松分布和零膨胀负二项分布的GAM 模型对一组实际车险索赔数据中的索赔次数进行研究分析，并对不同模型的预测效果进行比较，探究更为合理的预测方法，为车险索赔频率研究提供一定的参考。

一、预备知识

（一）车险索赔次数分布。用随机变量Y 表示保单的索赔次数，i=1，2，3…，若 Y 服从零膨胀分布，则根据 Yip 和 Yau（2005），其概率函数表示如下：

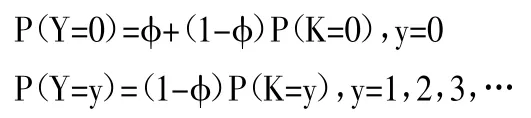
式中，φ 为发生事故但未索赔的概率，0＜φ＜1，K 为随机变量。

当随机变量K 为服从均值为μ 的泊松分布时，随机变量Y 服从零膨胀泊松分布（ZIP），其概率函数可表示为：

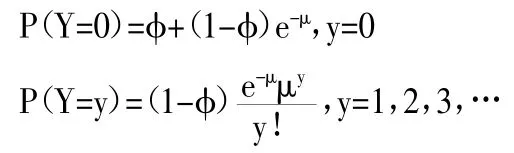
当随机变量K 为服从参数为r 和μ 负二项分布时，随机变量Y 服从零膨胀负二项分布（ZINBI），其概率函数可表示为：

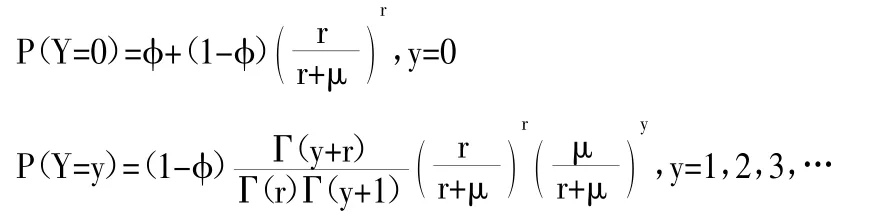
当φ=0 时，零膨胀分布退化为泊松分布和负二项分布。

（二）GAM 模型。设 YT=（Y1，Y2，…Yn）为响应变量的 n 维向量，其服从指数族分布。据Hastie 等（1986）所述，GAM 模型的结构表示如下：

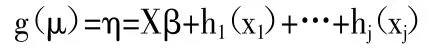
其中，μ 为响应变量 Y 的均值，g（·）为连接预测项 η 和均值 μ 的连接函数；向量X 为具有线性影响的解释变量，β 表示参数向量，则Xβ 为解释变量的线性影响函数；xj（j=1，2，…J）是具有非线性影响的解释变量，hj（·）是关于xj的非参数平滑函数。

（三）随机森林。随机森林是Breiman（2001）提出的一种以CART决策树为基础的集成学习模型。随机森林模型的适应性较强，不容易产生过拟合问题，它既可以用于分类也可以用于回归。随机森林的生成步骤如下：

1、用Bootstrap 方法从样本容量为K 的训练集中有放回地随机抽取等量的样本，作为一棵决策树的训练样本。

2、决策树由根节点开始自上而下递归分裂。在决策树的每个节点需要分裂时，从样本中的M 个特征（解释变量）中随机选取m 个特征（m＜M），再从m 个特征中挑选一个最优特征对节点进行分裂。

3、决策树的形成过程中每个节点均按照步骤2 进行分裂，直到节点无法继续分裂时停止。随机森林中的决策树都随意生长，不需要进行剪枝。

4、按照上述3 个步骤生成N 棵回归树，从而构成随机森林。在回归问题中，由森林中的每一棵决策树分别输出一个预测值，所有决策树的预测值的平均值即为随机森林的输出值。

随机森林的生成依赖于两个极为重要的参数，即随机选取的特征个数mtry 和随机森林中决策树的数量ntree，它们影响着随机森林模型的分类能力。

（四）模型评价

1、在选择GAM 模型时，本文采用AIC、BIC 准则进行比较。一般来说，AIC 和BIC 的值越小，模型的拟合效果越好。AIC 和BIC 的定义如下：

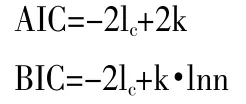
其中，lc是对数似然函数，k 是模型中未知参数的个数，n 是模型中的观测值个数。

2、本文使用均方根误差（RMSE）对随机森林和GAM 模型进行比较，其表达式如下：

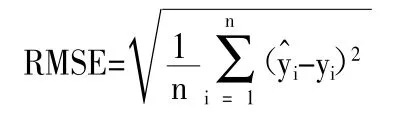
其中，yi表示观测值，表示模型预测值，n 是模型中的观测值个数。RMSE 表示预测值与实际观测值之间的平均偏差，其值越小，说明模型的预测效果越好。

二、实证分析

（一）数据描述与预处理。本文使用的是AutoClaim 数据集，该数据集是从SAS Enterprise Miner 数据库中检索的一组汽车第三方责任保险数据，其包含10，302 份保单和27 个变量。为了便于计算和减小模型预测误差，本文进行了变量筛选。首先，剔除无关变量ID（订单编号）、BIRTH（出生日期）、OLDCLAIM（累计索赔金额）和 CLAIM_AMT（当期索赔金额），然后采用向后逐步回归对其余变量进行降维。根据向后逐步回归的结果，本文选取了12 个变量作为解释变量，各解释变量及其具体信息如表1 所示。（表1）

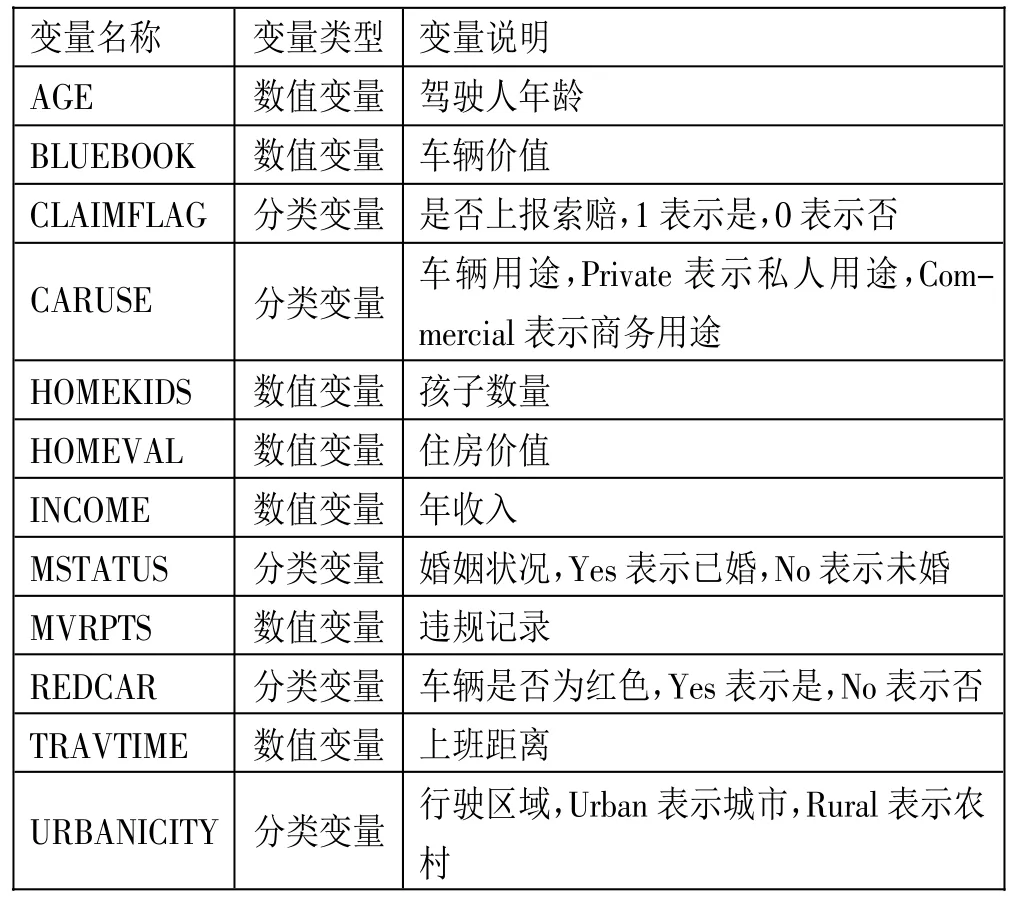
表1 解释变量及说明一览表

在处理缺失值和异常值后，得到的数据集包含7，647 个样本。进而，本文分别从索赔次数为 0、1、2、3、4、5 的保单中随机抽取 80%的保单形成训练集，其余20%的保单数据形成测试集。对索赔次数作简单统计，具体情况如表2 所示。（表2）

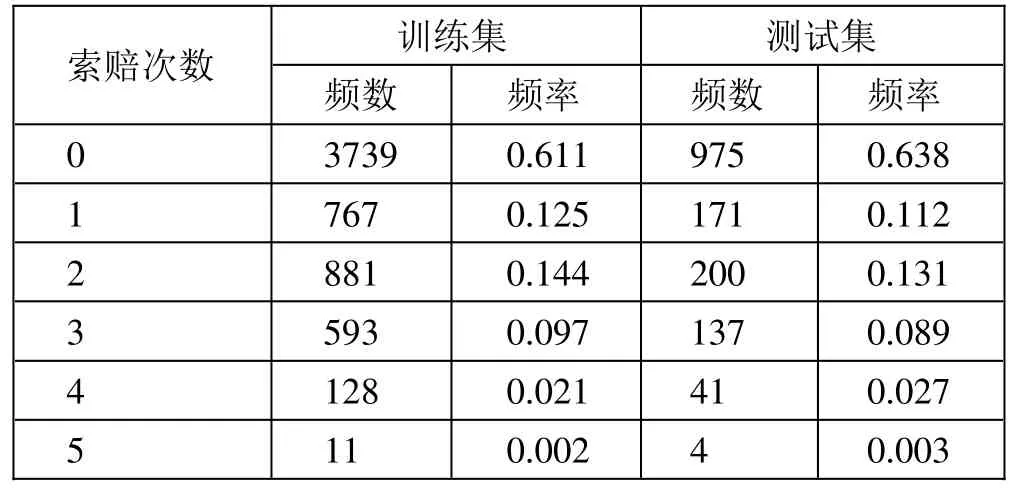
表2 索赔次数的频率一览表

表2 显示，在训练集和测试集中，均有超过60%的数据索赔次数为0，说明该组数据具有零膨胀特征。训练集中有12.5%的保单发生1次索赔，26.4%的保单发生2 次以上索赔，索赔次数为5 的保单出现频率最低，仅为0.02%；测试集中有11.2%的保单发生1 次索赔，25%的保单发生2 次以上索赔，索赔次数为5 的频率仅为0.03%。

（二）GAM 模型拟合。本文在索赔次数服从泊松分布、负二项分布、零膨胀泊松分布和零膨胀负二项分布的条件下建立GAM 模型。计算不同模型的AIC 值和BIC 值，结果如表3 所示。（表3）

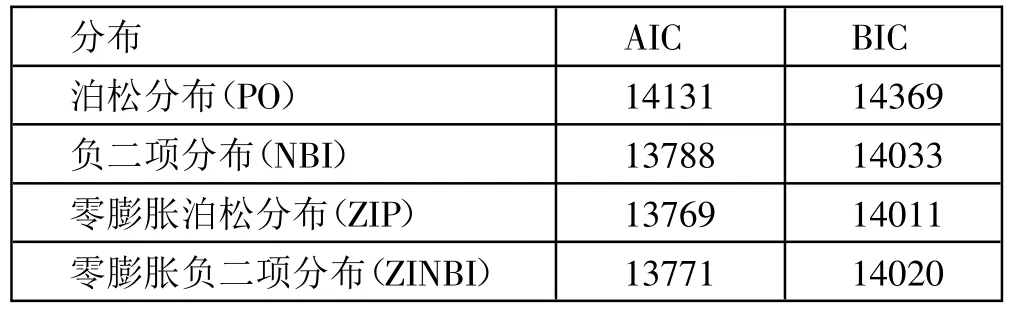
表3 不同分布下的模型拟合优度一览表

由表3 可知，零膨胀模型优于普通的泊松回归模型和负二项回归模型，且通过比较AIC 值和BIC 值发现，ZIP 分布下建立的GAM 模型拟合效果最优。本文对其进行参数估计，估计结果如表4 所示。（表4）

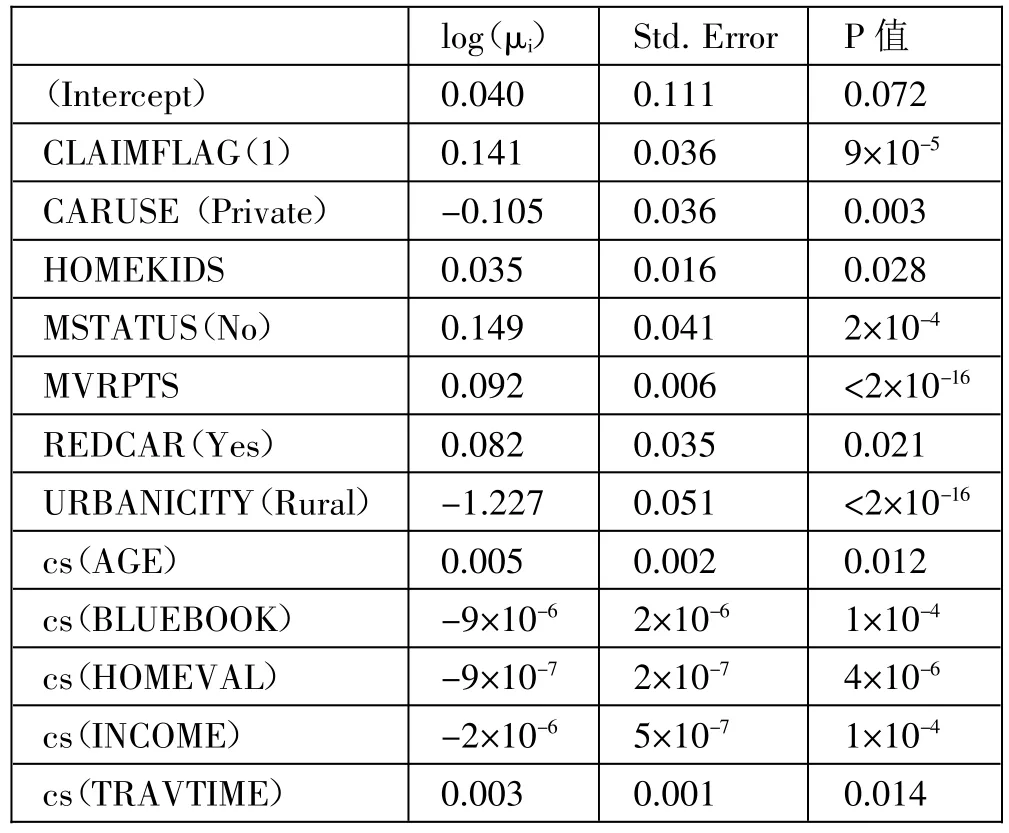
表4 参数估计一览表

根据参数估计表，在Yi服从零膨胀泊松分布下，得到的GAM 模型如下所示：

log（μi）=0.040+0.141CLAIMFLAG（1）-0.105CARUSE（Private）+0.035HOMEKIDS +0.149MSTATUS +0.092MVRPTS +0.082REDCAR -1.227URBANICITY （Rural）+cs （TRAVTIME）+cs （BLUEBOOK）+cs（HOMEVAL）+cs（INCOME）+cs（AGE）

可以看出，几乎所有解释变量都对均值有显著影响。上报索赔的投保人有较多的索赔次数；相对于商务车来说，私家车具有较少的索赔次数；对于已婚的投保人来说，未婚投保人的索赔次数更多；违规记录和孩子数量的系数为正值，说明违规记录和孩子数量越多的驾驶人发生索赔的次数越多；红色车辆发生索赔的次数比其他颜色的车辆更多；而在乡村行驶的车辆索赔次数比城市更少。表4 中的非参数变量系数及其标准误差仅指平滑器的线性部分，且这五个非参数变量无法简单地用数学形式描述，画出其对索赔次数的影响效应图，具体如图1所示。图（a）、（b）、（c）、（d）、（e）分别表示驾驶人年龄、上班距离、住房价值、年收入和汽车价值对索赔次数的影响，图中横坐标表示解释变量的实测值，纵轴表示平滑函数值，阴影表示置信区间上下限，中间实线表示索赔次数的平滑拟合曲线。通过图1 可以发现，驾驶人年龄和上班距离对索赔次数的影响较为平稳；随着住房价值的增加，索赔次数略有下降，随后变得平稳；年收入与索赔次数呈现非常强烈的非线性关系，索赔次数处于波动状态；车辆价值与索赔次数呈负相关，车辆价值越大，索赔次数越少。（图1）

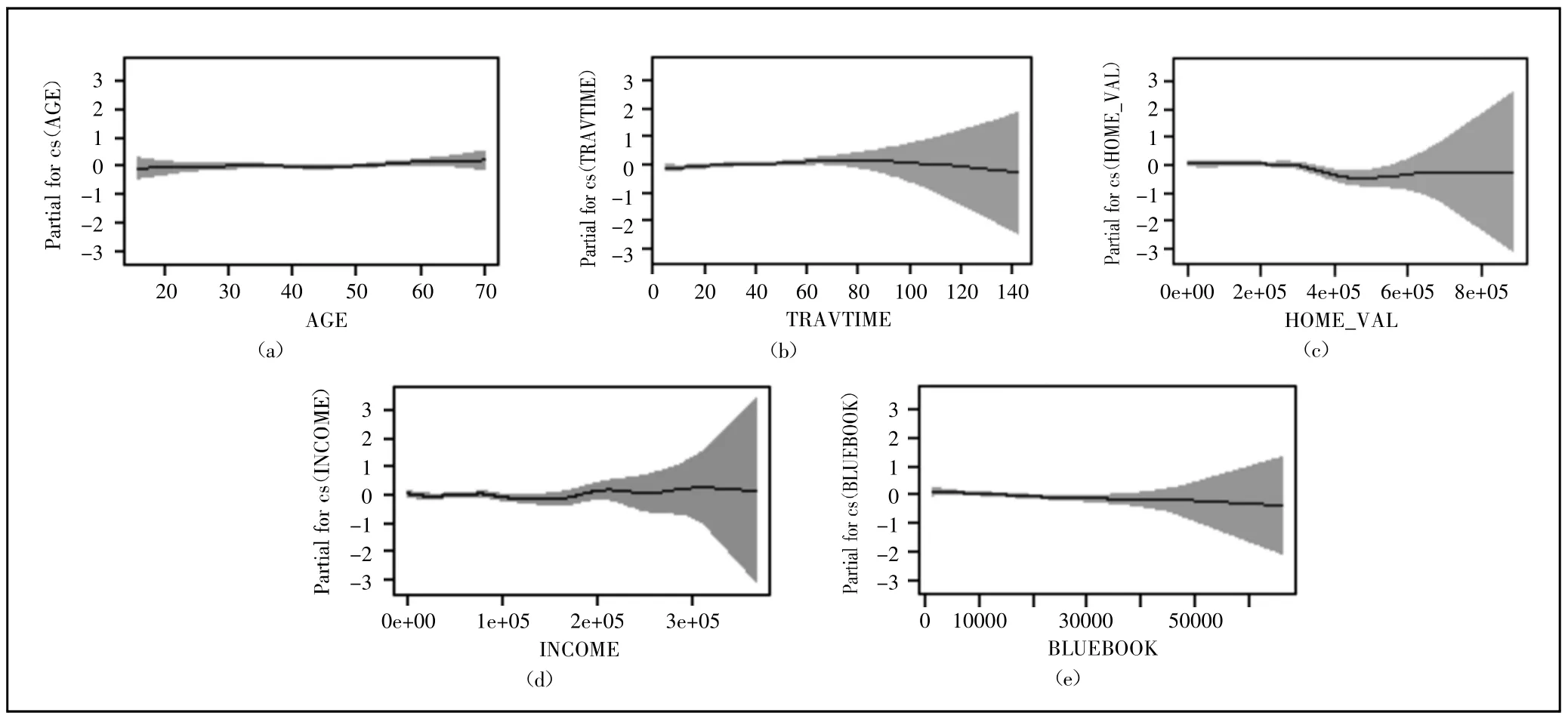
图1 影响效应图

（三）随机森林的构建。随机森林模型可以用R 语言中的random-Forest 包实现。在利用训练集建立随机森林模型之前，需要使用十折交叉验证来寻找使模型均方根误差（RMSE）最小的最优参数mtry 和ntree，mtry 是指树节点用于分裂的变量个数，ntree 是指随机森林所包含的决策树数目。

首先，根据RMSE 确定最佳mtry 值。本文解释变量有12 个，故将mtry 参数设置为1～12 进行建模，计算不同mtry 取值下的RMSE 值，RMSE 随着mtry 的变化如图2 所示。可以看出，随着mtry 的值增大，RMSE 的值先减小后增大，在mtry 的值为2 时，RMSE 的值最小，因此本文选择2 作为最优mtry 值。（图2）

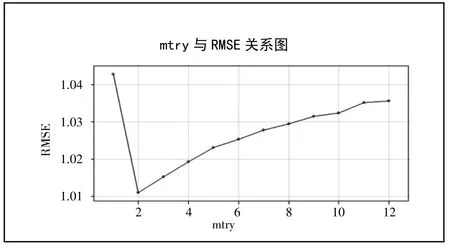
图2 mtry 与 RMSE 关系图

其次，根据RMSE 确定最佳参数ntree。在mtry=2 的条件下，使ntree 分别等于 100，200，…，1000，依次计算 RMSE 的值，绘制 RMSE与ntree 的关系图，如图3 所示。（图3）

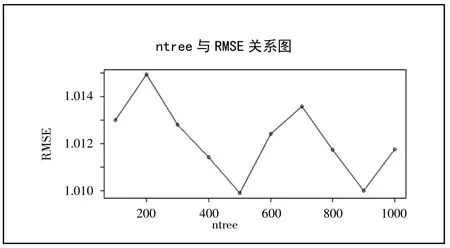
图3 ntree 与 RMSE 关系图

从图3 可以看出来，当ntree 的取值为500 时，RMSE 的值最小。故本文选择500 作为ntree 参数的取值。经过交叉验证，索赔频率预测模型的最优参数为mtry=2，ntree=500。以此参数建立随机森林模型，并用该模型对测试集进行预测。

（四）模型比较。本文将ZIP 分布和ZINBI 分布假设下的GAM 模型以及随机森林模型用于测试集中，并计算各自的RMSE。（表5）

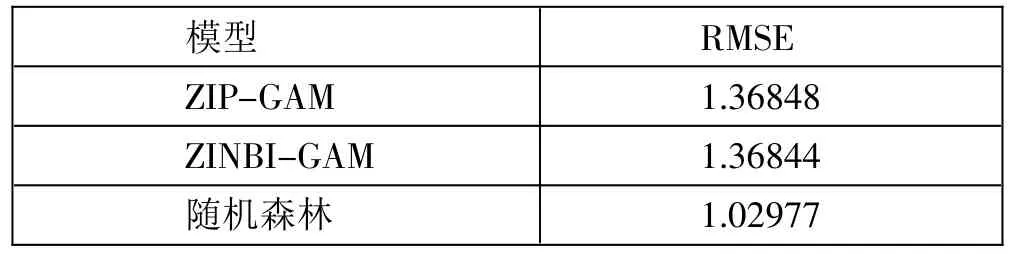
表5 各模型RMSE 一览表

如表5 所示，发现ZIP-GAM 模型的预测效果最优，其次是ZINBIGAM 模型。相比之下，随机森林的预测效果最差，这可能在于索赔次数数据不平衡，导致模型训练受到影响，进而影响了模型的预测效果。

三、结论

本文对一组实际车险索赔数据分别建立GAM 模型和随机森林模型，并进行了比较分析，结果表明基于零膨胀泊松分布假设下的GAM模型比随机森林在费率厘定中具有更大的优势。相比之下，GAM 模型不仅具有更好的预测能力，而且其对预测结果的可解释性比随机森林模型强，可以清晰地展示出每个解释变量对索赔次数的影响程度。但随机森林也有一定的优越性，在其建模前不需对数据进行预处理。

综上，随机森林和GAM 模型各有优点，在实际生活中可以根据不同的条件选择合适的方法。同样的，这两种模型也能应用于索赔强度或保费定价中，对保险公司的费率厘定和客户选择有一定的参考价值，以改进费率厘定结果的合理性。