高速铁路长大坡道动车组运行性能分析方法

胡彦霖 ，凌 亮 ，王开云

（西南交通大学牵引动力国家重点实验室，四川 成都 610031）

近年来，我国高速铁路工程的建设重心开始向中西部山区丘陵地带转移，受地理环境限制，需修建大量长大坡道来克服复杂的地形地势条件. 例如，西安—成都高速铁路（西成高铁）15‰以上坡道共有24处，长度超过5.0 km的坡道有10段，而其中鄠邑—新街场区间的25‰大坡道长达45.1 km；成都—贵州高速铁路15‰以上坡道共有47处，长度超过5.0 km的坡道也达到10段，最大坡度达到30‰. 当高速动车组经过长大坡道时，上坡道的附加阻力会使得列车的运行速度降低，而下坡道的巨大惯性则可能会引发列车超速. 长大坡道上列车运行速度的大幅度变化不仅影响线路的运营调度管理，也会影响列车通过平面曲线的安全性和轮轨磨耗性能. 因此，建立高速列车与坡道的耦合动力学模型，开展超长大坡道上高速列车的运行性能研究，提出高速动车组功率配置与线路坡道匹配设计方法及超长大坡道上高速列车安全运行保障技术，对于我国高速铁路进一步向中西部扩展以及我国高速列车安全保障技术的进一步提升均有着积极的作用.

为指导线路规划设计与运输组织，往往需要对运营列车在指定线路上的运行性能进行分析. 由于一维的单质点或多质点模型无法反映列车运行时的车辆与轨道的耦合振动行为，故在计算时会产生一定的误差，且误差会随仿真时长的增加不断累积，对结果产生较大影响. 随轨道交通规模不断扩大，线路条件日益复杂，一维模型在进行长大坡道列车运行性能分析、列车牵引与制动性能分析等方面的局限性已开始显现. 国内外学者对列车在长大坡道上的运行性能开展了研究. 根据理论研究与试验数据，优化了一维模型，使其对列车运行速度变化的计算结果更符合实际情况[1-3]. Albrecht等[4-5]以节能策略寻优为目的，在传统一维模型的基础上考虑了连续控制策略，对连续长大坡道上列车运行的最优控制方法与相应的速度曲线进行了分析. Ding等[6]基于列车牵引计算理论与实测数据，提出了长大坡道列车运行阻力的修正计算方法. 随仿真技术的发展与计算机计算能力的不断提高，采用多体动力学计算软件，建立车线耦合模型，对车辆在线路上的运行性能进行评估也逐渐成为常用的分析手段. 易思蓉等[7]基于动力学理论，建立了一种基于车线动力学性能的高速铁路最小曲线半径分析方法，给出了高速客运专线最小曲线半径标准建议. 王仲林等[8]采用车辆-线路系统动力学与有限元方法，分析了40‰最大坡度对地铁车辆行车特性的影响. 这类方法在进行动力学性能分析时，通常无法考虑轨道系统振动对车辆-轨道大系统的影响. 当线路较长时，采用动力学仿真软件建立的动车多节编组模型在计算速度方面也不具备优势. 基于车辆-轨道耦合动力学理论[9-10]可以对列车运行过程中车辆与轨道结构的振动响应进行计算，部分学者将此理论应用于列车运行性能分析，提出了三维的列车运行性能分析方法. 王开云等[11]基于该理论，采用系统工程思想，对匀速条件下高中速客运专线和高低速客货共线铁路平纵断面的合理匹配进行了研究. 凌亮等[12-14]建立了考虑牵引与制动的高速列车-轨道三维刚柔耦合动力学模型，分析了高速列车变速移动状态下的振动响应特征，为长大坡道高速列车动力学行为的数值模拟提供了研究思路. Hu等[15]搭建了考虑线路坡道的车辆-轨道耦合动力学数值模型，研究了坡道对动车组运行性能的影响. 采用车辆-轨道耦合动力学理论能更加全面、真实地分析车辆-轨道系统的动力学特性、预测编组列车在长大坡道上的速度变化；通过建立的数值模型，能对编组条件下的高速列车动力学性能进行更高效的计算.

本文基于车辆-轨道耦合动力学理论，考虑列车振动、轮轨黏滑振动与长大坡道作用，搭建动车组运行性能分析模型，提出一种考虑列车与线路耦合振动的高速铁路长大坡道动车组运行性能分析方法. 根据试验结果，分别对仿真模型的速度曲线计算结果与车体振动加速度计算结果进行验证.基于西成高铁运营初期CRH3A动车组长大坡道运行时降速严重的工程问题，考虑列车实际的牵引与制动特性，对不同功率等级下列车运行通过长大坡道时的速度与运行安全性指标进行计算，根据计算结果，为西成高铁长大坡道线路运营提供科学的车线匹配建议.

1 列车-轨道耦合动力学模型

为对长大坡道动车组运行性能进行更准确地分析，基于车辆-轨道耦合动力学理论[10]建立了考虑动车组实际牵引制动特性与长大坡道作用的动车组运行性能分析数值模型. 采用自编程方式构建列车-轨道耦合动力学模型时，每节车辆被简化为由1个车体、2个构架和4个轮对组成的多刚体耦合系统，每个部件考虑纵向、横向、垂向、侧滚、点头和摇头6个方向的自由度. 轮对和构架件通过一系悬挂连接，一系钢簧及转臂节点和牵引拉杆采用线性的弹簧单元模拟；构架和车体通过二系悬挂连接，二系空簧采用并联的弹簧-阻尼单元模拟，横向止挡采用非线性的弹簧单元模拟；一系垂向减振器、二系横向、垂向减振器及抗蛇行减振器均采用串联的弹簧-阻尼单元模拟，抗侧滚扭杆采用线性的扭转弹簧模拟.车辆间通过车间悬挂部件相连，车钩缓冲装置简化为只沿轴向伸缩的空间二力杆，车间减振器模拟为非线性的阻尼单元. 根据列车牵引与制动特性曲线，将牵引或制动力以力矩的形式施加于每个轮对的车轮中心；根据部件的质量与线路坡度，计算各部件位于坡道时的重力分量.

轨道模型参考无砟轨道结构建立，主要由钢轨、扣件系统、轨道板和轨道板下支承结构组成. 其中，钢轨简化为连续弹性离散点支承的Timoshenko梁，考虑垂向、横向及扭转运动自由度；轨道板采用三维实体有限元单元进行离散，采用模态叠加方法进行求解；钢轨扣件采用线性的弹簧-阻尼单元模拟；不考虑底座板和路基的振动行为，将轨道板下支承结构考虑成连续的粘弹性单元.

轮轨空间动态的接触几何关系基于考虑轮轨弹性的新型轮轨接触几何数值算法[10]进行求解；采用赫兹非线性弹性接触理论求解轮轨法向力；根据Kalker线性蠕滑理论计算轮轨蠕滑力，在轮轨间蠕滑达到饱和后，采用Shen-Hedrick-Elkins理论进行非线性修正.

车辆-轨道耦合动力学模型的搭建与系统运动方程的推导详见文献[9,10,12]，在运动方程中，考虑了坡度变化对车体、构架与轮对振动响应的影响. 以车体为例，忽略坡道导致的车体姿态变化，考虑坡道对重力的影响，其在纵向（x）、横向（y）、垂向（z）上的振动方程分别如式（1）～（3）所示.

式中：Mc为车体质量；V为列车运行速度；a0为左右轮接触点之半；Htw为构架质心至轮对中心的垂直距离；HBt为构架质心至二系空簧下平面的距离；HcB为车体质心至二系空簧上平面的距离；r0为车轮名义滚动圆半径；g为重力加速度；iramp为线路坡道；Rc为圆曲线半径；Rv为竖曲线半径；为车体纵向加速度；为车体横向加速度；为车体垂向加速度；φsec为曲线轨道上车体中心所对应的外轨超高角；Fksaij（k=x,y,z；i= L,R，分别表示左、右方向；j= 1,2，分别表示前、后转向架）为二系空气弹簧作用力；Fkdio（o= f,b，分别指运动车体的前车、后车）为车间减振器作用力分力；FySTj为二系横向止挡作用力；Fksdij为二系抗蛇行减振器作用力；FxTBij为二系牵引拉杆作用力；Fkco为运动车体受到的车钩作用力；Fkwo为运动车体受风挡的作用力.

线路平纵断面是决定长大坡道动车组运行性能的关键因素. 与直线相比，平面曲线主要考虑平面曲线和曲线超高对轮轨接触关系的影响以及离心力对车辆系统振动的影响. 在纵断面上，主要考虑坡度变化对轮轨接触关系与车辆系统重力分量的影响：首先，将线路坡度表示为随线路长度变化的函数，竖曲线的影响被简化为竖曲线不同位置处线路坡度的变化[16]；其次，在构建系统振动控制方程时，根据车体、构架、轮对的质量与线路坡度，考虑了由坡道导致的重力分量变化对车体、构架、轮对纵向与垂向振动的影响，重力分量在方程中被表示为与坡道有关的函数. 根据以上建模思路，搭建的长大坡道动车组运行性能分析模型的整体结构如图1所示.

图1 长大坡道列车-轨道耦合动力学模型Fig. 1 Train-track coupled dynamic model on long steep grade

2 模型对比分析与验证

高速列车牵引运行条件下，轮轨牵引力使得轮轨间产生微小的滑动，轮轨摩擦滑动消耗部分的牵引能量；同时轮轨几何不平顺会使得轮轨法向载荷出现波动，导致轮轨黏着力及轮周牵引力产生波动，使得轮轨黏滑振动耗能加剧. 此外，轮轨波动产生的车辆系统振动也会使得车辆间的悬挂部件消耗部分的牵引能量，从而使得列车的牵引效率降低. 即忽略列车轨道系统的振动会高估列车的牵引效率. 图2给出了CRH2和CRH380AL动车组分别以250 km/h和350 km/h的目标运营速度通过捞村—荔波区间25‰坡道时的速度曲线. 三维模型在计算时采用中国高速无砟轨道不平顺谱[17]模拟线路不平顺. 由图可知，三维模型所预测的坡道降速结果大于一维模型计算结果，两者误差在5%左右，其原因在于三维模型考虑了列车与轨道的耦合振动作用对爬坡过程中轮对牵引的影响. 高速列车变速运行条件下，轮轨几何不平顺引发的列车轨道系统振动会使列车牵引效率降低，因而，三维模型的计算结果更接近真实情况.

图2 CRH2和CRH380AL通过25‰坡道的速度曲线Fig. 2 Speed curves of CRH2 and CRH380AL passing through section with the grade of 25‰

为进一步验证本文所建立的模型的可靠性，将动车组运行速度的测试数据与模型的计算结果进行了对比，如图3所示. 通过GPS测速仪对某型动车组在线路运行时的速度数据进行了采集. 仿真计算时采用了该车型的设计牵引和制动力曲线施加牵引与制动力，根据线路参数设置了平纵断面与分相区.由于实测过程中，在63 s前与1215 s后司机施加了操纵，故本文仅对63～1215 s的速度曲线进行了验证.

图3 列车速度曲线对比Fig. 3 Comparison of speed curves

图4将某型高速动车组在武广线运行时，列车头车车体的横向加速度和垂向加速度测试数据与三维模型计算得到的车体横向和垂向振动加速度响应进行了对比验证，仿真采用了武广线实测线路不平顺样本. 在分析时，对车体振动加速度的测试数据进行了截止频率为40 Hz的低通滤波.

由图3和图4可知：仿真计算得到的列车运行速度曲线与现场实测结果基本一致，现场实测车体垂向与横向振动加速度的变化趋势与仿真计算结果吻合较好. 这一方面表明本文所建立的模型可以准确模拟出列车在牵引、制动与坡道运行工况下的列车运行速度变化，另一方面也表明该模型可以较好地反映运行过程中列车系统的振动响应特征.

图4 试验结果与仿真结果对比Fig. 4 Result of comparison of test and simulation

3 应用实例

西成高铁是典型山区高速铁路，其拥有生态环境要求严格、气候地质环境艰险、运营和维护安全标准高等特点，是目前我国已建成运营高速铁路中坡道最多、长大坡道最长、特长隧道最多的高速铁路.西成高铁西安—江油段包括15‰以上坡道共有24处，长度超过5.0 km的坡道有10段，而其中鄠邑—新街场区间的25‰大坡道长大45.1 km. 西成高铁设计主要采用以CRH3A为主的250 km/h速度级动车组. 实际运营后，既有250 km/h速度级动车组在长大坡道上速度损失很大，牵引适应能力差，无法满足运用部门要求. 长大坡道的降速现象不仅会影响到线路的运营效率，还有可能影响到动车组的曲线通过性能，危及行车安全，因而有必要对动车组的长大坡道运行性能进行更可靠的分析. 在西成高铁14个区间中，有6个区间的长大坡道里程占到了区间里程的25%以上，其中长大坡道占比最高的达到了区间里程的89.2%. 这6个区间的长大坡统计如表1所示.

表1 西成高铁超长大坡道统计Tab. 1 Statistical result of long steep grades in Xi’an−Chengdu high-speed railway

利用建立的长大坡道动车组运行性能分析模型，对CRH3A型动车组通过西成高铁全线区段的运行速度及区间用时进行精确计算，分析牵引功率对动车组通过西成高铁全线运行性能的影响，以支撑西成高铁动车组选型研究.

为分析CRH3A动车组通过长大坡道时的运行性能，应用本文建立的动力学分析模型，根据牵引与制动特性曲线施加牵引与制动力，将西成高铁平纵断面参数与动车组参数输入模型进行计算. 仿真时采用的线路谱为中国高速无砟轨道不平顺谱[17], 考虑轨道的轨距、水平、轨向与高低不平顺. 动车组以到站不停车（直通）和到站停车（站停）的方式通过鄠邑—新场街区间的速度曲线仿真结果如图5所示. 由图可知：在原功率方案下，CRH3A型动车组以直通和站停的方式通过该长大坡道区间时，均会产生较为严重的降速现象.

图5 CRH3A按原功率通过鄠邑—新场街区间的速度曲线Fig. 5 Speed curves when CRH3A passing through Huyi−Xinchangjie with original power

图6给出了以直通的形式通过区段A曲线地段时动车组头车一位轮对的轮轴横向力、脱轨系数和轮重减载率. 该区段曲线半径8000 m，缓和曲线长240 m，曲线外轨超高150 mm.

图6 CRH3A以原功率通过区段A的运行安全性指标Fig. 6 Wheel-rail safety index when CRH3A passing through section A with original power

图6表明：严重掉速会使列车通过曲线时的动力学性能受到影响，随着动车组速度降低，轮轴横向力呈增大的趋势，最大值为16.7 kN，曲线内侧车轮脱轨系数的值随速度降低而增大，最大值为0.21，减载侧车轮的轮重减载率值也随动车组通过速度的降低呈增大的趋势，最大值为0.31. 在既有的线路设计方案下，动车组无法以目标速度通过线路区间可能会对线路运营与行车安全带来不利影响. CRH3A型动车组的曲线通过安全性较好，但其在长大坡道上的运行速度无法满足线路运营需要，应考虑提升列车牵引功率或选择更高功率的动车组.

图7给出了CRH3A动车组功率提升10%～50%后，以站停和直通的方式通过该区间时的速度曲线，初始功率及提升10%、15%、20%、25%、50%分别对应5500、6050、6600、7150、7700 kW. 从图可以看出：对于当前考虑的功率方案，CRH3A动车组达到坡顶的速度均不到200 km/h，即无法达到坡顶降速量小于20%的要求；当初始功率提升50%，对应动车组功率为8250 kW时，列车坡顶速度接近200 km/h，但整个运行过程中的平均速度仍然低于200 km/h，最高速度也远低于250 km/h.

图7 CRH3A以不同功率通过鄠邑—新场街区间的速度曲线Fig. 7 Speed curves when CRH3A passing through Huyi−Xinchangjie with different powers

采用150%功率方案后的动车组直通通过区段A时，动车组头车一位轮对相应车轮的轮轨横向力、脱轨系数和轮重减载率如图8所示. 牵引功率提升后，动车组在长大坡道上运行时的降速减缓. 通过曲线区段过程中，一位轮对的轮重减载率的变化不明显，其最大值为0.31，最大轮轴横向力与最大脱轨系数的绝对值略微降低，其值分别为14.98 kN与0.19，列车的曲线通过安全性略有提高. 由于西成高铁设计标准较高，严重降速区域的线路圆曲线半径均在7000 m以上，在仿真时也并未进一步分析列车载重变化与线路小半径曲线对动车组长大坡道运行性能的影响，故采用高速铁路长大坡道动车组运行性能分析方法得到的列车运行安全性指标数值均较低.根据计算结果，提高列车牵引功率，缓解了高速列车在长大坡道运行时的降速现象，但对列车曲线通过安全性指标的降低作用并不明显.

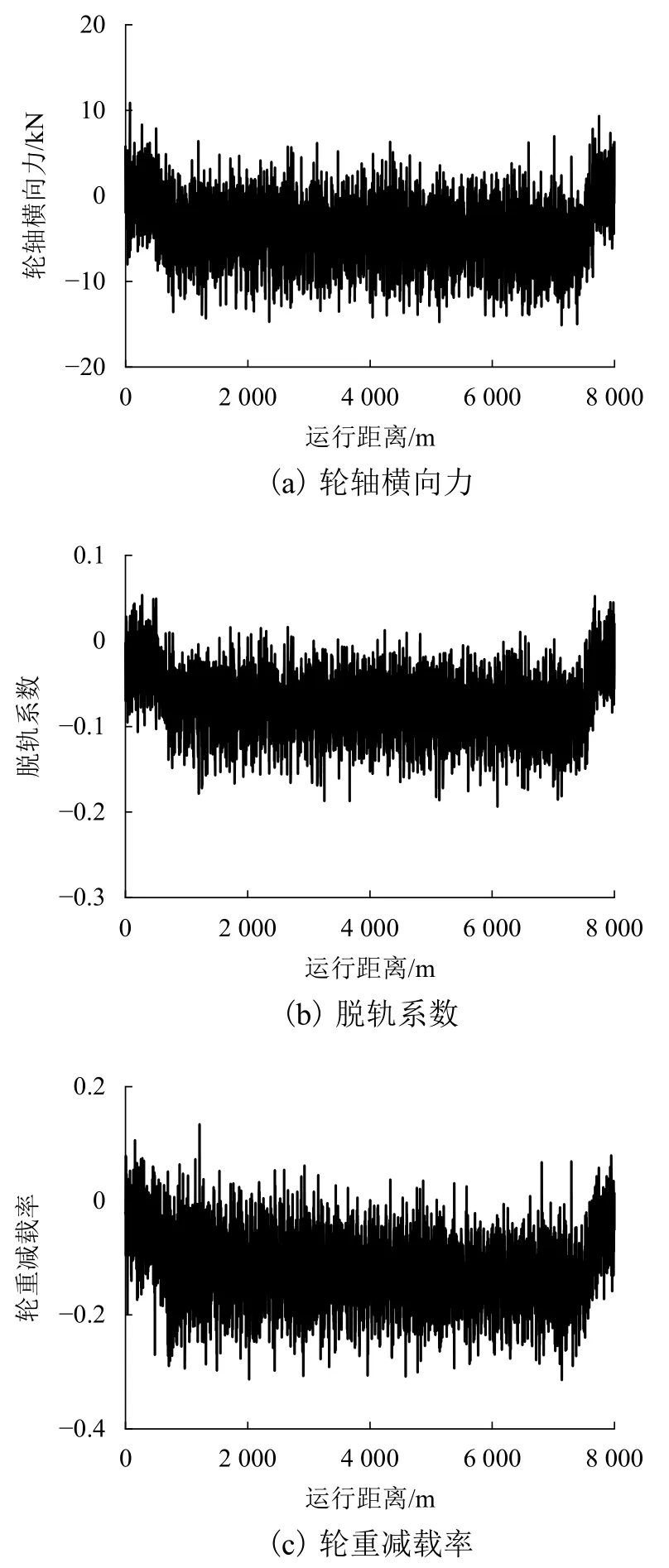
图8 CRH3A功率提升50%后通过区段A的运行安全性指标Fig. 8 Wheel-rail safety index when CRH3A passing through section A with 1.5 times of power

仿真结果表明，提高列车牵引功率能有效提高动车组长大坡道的通过速度,有助于提升动车组的曲线通过性能. 在列车原功率方案的基础上，功率提升越高，单列动车组的改造成本也越高，根据仿真结果，在功率提升50%后，CRH3A型动车组的长大坡道运行性能仍然较差. 实际运营过程中，环境风、隧道、分相、线路黏降等都会对列车长大坡道牵引与制动能力的发挥产生影响. 结合仿真结果与线路的实际运营状态，可以考虑选择功率更高的动车组投入运营.

由于存在动能闯坡的情况，与站停通过的方式相比，动车组以直通的方式运行通过各区间的最小坡顶速度更大，通过各区间的用时更短. 正常运营条件下，动车组以站停的方式正常运送旅客的情况更为常见. 故仅采用高速铁路长大坡道动车组运行性能分析方法，对西成高铁江油—西安北14个区间，CRH3A动车组以站停的方式上、下行通过各区间时的最小坡顶速度、区间用时进行了计算，如表2所示. 表中：上行为西安北—江油，下行为江油—西安北. 由表可以看出：在原功率方案下，动车组以站停的方式通过各区间，在上、下行范围内，坡顶降速超过50 km/h的区间均达到了7个. 在不考虑进站停车时间的情况下，动车组全程的平均速度为185 km/h左右. 表3、4分别给出了CRH3A动车组以不同功率方案站停通过西成高铁西安北—江油区段14个运行区间时降速超过20%的区间数量和区间用时统计值. 结果表明，CRH3A动车组通过西成高铁14个坡道区间时，站停运行方案下坡顶速度损失超20%的区间数量达到7个，占区间总数的50%；提升列车牵引功率能有效减小西成高铁长大陡坡上列车运营速度的损失；当CRH3A按现设计功率（5500 kW）以及功率分别提升10%、15%、20%、25%、50%方案运行时，西成高铁14个运行区间中动车组在长大坡道上速度损失超过20%的区间数随着功率增加而减小；提升牵引功率能有效减小动车组区间运行用时；当CRH3A按现设计功率以及功率分别提升10%、15%、20%、25%、50%方案运行时，在不考虑进站停车时间的情况下，动车组通过西成高铁14个区间的总用时随着功率增加而减小，增加动车组牵引功率为缩短线路运行时间提供可能. 结合上述分析可知，原始功率方案不能保证CRH3A型动车组在西成高铁上的正常运营，为提高西成高铁的运行效率，需采用牵引功率更高的动车组.

表2 最小坡顶速度与区间用时统计结果Tab. 2 Statistical results of minimum speeds on uphill and time cost

表3 坡顶降速超20%的区间数量（站停）Tab. 3 Amount of sections where the reduction of speed over 20% while the train stop at every station 个

表4 CRH3A通过各区间的用时统计Tab. 4 Statistics of time cost of CRH3A at each section min

4 结 论

本文提出了一种采用三维列车-轨道耦合动力学模型分析高速铁路长大坡道动车组运行性能的方法. 相对于传统一维模型，考虑了列车振动、轮轨黏滑振动与长大坡道影响的三维模型能更准确地反映列车通过长大坡道时的真实情况. 本文所提出的分析方法可为动车组通过长大坡道时的牵引制动性能、运行安全性与平稳性评估以及线路科学设计等提供更可靠的分析工具.

基于仿真计算，对CRH3A型动车组通过西成高铁时的运行性能进行了详细分析. 结果表明：CRH3A型动车组在西成高铁长大坡道运行时会出现严重的降速现象，对列车的曲线通过安全性产生不利影响；提升牵引功率能缓解降速情况，从而提高列车曲线通过安全性；据此，提出了在西成高铁使用更高牵引功率动车组的建议.