一种基于零模编码的CT图像恢复算法
2022-04-21董正山
董正山,林 耿
(闽江学院数学与数据科学学院(软件学院), 福建 福州 350108)
0 引言
图像在一些变换(如小波变换、curvelet变换等)下是可以稀疏表示或压缩的,从而可以用稀疏编码的方法研究图像处理中涉及到的问题[1-2],如可以用稀疏优化的方法分析图像的超分辨率、图像的去噪、以及图像恢复等问题。
假设I表示图像,Ψ表示稀疏变换,且图像I在该变换下是稀疏或可压缩的,即有I=Ψx,其中,x有较多的零分量(稀疏性)或较多较小的分量(可压缩性),Φ表示采样矩阵,从而观察到的数据可以表示为y=ΦΨx+σ,其中σ表示噪声。为了从观察数据y中恢复原始图像I,根据问题的稀疏性特点,可建立如下求解模型:
其中,‖·‖0表示向量中非零元素的个数,其被称为零模或“零范数”,s>0控制变量的稀疏性。通过模型(1)求解出变量x后,就可以通过I=Ψx恢复出原始图像。但是问题(1)的最优解主要任务是找准非零分量的位置,这是一个组合优化问题,且是NP-hard问题[3]。为了求解该稀疏优化问题,目前主要的方法有贪心算法、松弛算法、混合网模型算法、基于零模的算法等。
主要的贪心算法有匹配追踪(MP)算法[4-6]等,这些算法可以用于准确快速地解决无噪声的小规模问题,但不适于解决有噪的或大规模的问题。松弛算法主要是为解决难以处理的(离散的非凸的)“零范数”问题。松弛算法又分为凸松弛和非凸松弛,代表分别有(重加权)l1范数松弛[7-13]和lp“范数”(0 非凸松弛算法主要是lp“范数”模型算法。与l1范数模型算法相比,lp“范数”模型可以得到更加稀疏的结果,所需采样率比l1范数模型低。但由于是非凸优化,求的解只是算法的一个鞍点或不动点,算法设计可能更复杂。 混合网模型算法主要是同时考虑多种范数模型的优化算法,如混合范数模型同时考虑两种范数(l1和l2范数)模型等[16]。这些算法结合了不同范数算法的优点,取得了较好的效果。但这些方法还是没有直接求解“零范数”问题模型,得到的解可能并非稀疏解。 基于“零范数”的算法直接求解“零范数”优化模型,可以得到更稀疏的解。这类算法的代表有基于硬阈值算子的迭代方法[17-22]。由于硬阈值算子可以得到更稀疏的解,本文将利用迭代硬阈值方法求解问题(1)的子问题。 本节研究问题(1)的对偶问题。考虑到问题(1)的拉格朗日函数 (2) 以及对偶函数 (3) (4) 根据这两个性质,本文将设计基于拉格朗日和硬阈值迭代的求解算法。 硬阈值迭代算法可以用于求问题(3)中最小化问题的解,即给定λ值时求对偶函数的值。求对偶函数值的关键是求解“零范数”正则化问题,虽然该问题也是一个NP难问题,但可以使用迭代硬阈值算法求解。在迭代过程中,该方法为了使得问题可解,在当前点近似f(x),即 (5) 从而关于x的最小化问题可以变成变量可分离结构,对偶函数中最小化问题即可近似用下面子问题求解 (6) (7) 通常L取函数f(x)的李普希兹常数上界,但有时候这个上界不易求解,下面主要通过一个线搜索算法[19]找到一个合适的Lk,算法1中给出了求解对偶函数中最小化问题的迭代硬阈值算法。 算法1 线搜索的迭代硬阈值算法 输入:x0,λ,L0,Lmin,Lmax 输出:x* 1)初始化,k=0,γ>1; 2)通过线搜索找到Lk; 4)如果达到终止条件,终止算法,否则转到2。 本节中介绍利用拉格朗日方法和迭代硬阈值算法求解问题(4)。根据性质1,一个较大的λ值,可以得到更稀疏的解;相反,一个较小的λ得到一个相对稠密的解。所以在迭代过程中,发现当前解的非零元素的个数大于s,即所得的解较稠密。根据性质2,这时候适当地增加λ的值,使得更新后的解尽量满足原问题的约束;若在迭代过程中,当前解的非零元素的个数小于s,即所得的解可能过于稀疏,此时需要减少λ的值。这样通过这种搜索的方法,最终可以得到满足原问题的一个稀疏解。求解问题(1)的算法框架流程如下。 算法2 基于拉格朗日方法的图像恢复算法(LIHT) 输入:x0,λ0,L0,Lmin,Lmax 输出:x* 1)初始化,k=0,γ>1; 2)调用算法1获得当前解xk; 3)计算当前解非零元素的个数nk,如果nk>s,增加λ的值,否则减小λ的值; 4)如果满足终止条件,终止算法,否则转到2。 文[23]中指出,在一定的条件下,算法2可以得到原问题的一个L-稳定点。 本节通过在不同的采样率下恢复CT图像来说明本文提出算法的有效性。本文实验都是在Windows10系统(Intel(R) Xeon(R) W-10885M CPU @ 2.40GHz,内存32G)中使用工具Matlab完成。 实验采用标准的Shepp-Logan图像来完成CT图像的恢复,Shepp-Logan图像的大小是256×256(图1中左上角的第一张图是原图)。本实验中用不同的径向切片在星形域上通过二维的离散傅里叶变换采样层析数据,并用逆Haar小波变换作为稀疏化变换Ψ,设定s=3 769。图1、图2给出了本文提出的算法LIHT与其它算法(文[20]中的AIHTCG, 文[21]中的DORE,文[22]中的NIHT,文[24]中基于l1范数的方法FPCAS)的实验对比,包括算法运行时间以及PSNR值。 图1 各比较算法恢复CT图像时运行时间及恢复图像的PSNR值Fig.1 Running times and PSNR value of all compared method on CT images 图1展示了采样率为0.176时的结果对比。从图1中可以看出,本文提出的算法LIHT获得了最大PSNR值,虽然算法时间上略微比AIHTCG和DORE多一些,但可以接受。LIHT比NIHT和FPCAS在时间和PSNR上都有优势。图2展示了在不同的采样率下各对比算法取得的PSNR值,相应算法的运行时间在图3中给出。对比发现,在采样率较小时,FPCAS有些PSNR值的优势,但算法耗时较多。当采样率适当增大时,本文给出的算法更有PSNR值的优势。 图2 各比较算法在不同采样率下恢复CT图像时的PSNR值Fig.2 PSNR value of all compared method on CT images reconstruction under different sampling ratio 图3 各比较算法在不同采样率下恢复CT图像时的运行时间Fig.3 Running time (second) of all compared method on CT images reconstruction under different sampling ratio 首先,本文通过分析建立的稀疏约束问题的对偶问题,找到从对偶问题出发求解原约束问题的方法。该方法结合迭代硬阈值算法和对偶问题的特点,设计出有效的求解算法;最终通过数值实验验证了本文算法的有效性。后期将继续研究使用增广拉格朗日方法及邻近点算法求解稀疏约束的CT图像恢复模型,并将模型应用于胸部CT识别新冠肺炎病变等场景。1 模型分析
1.1 拉格朗日对偶问题
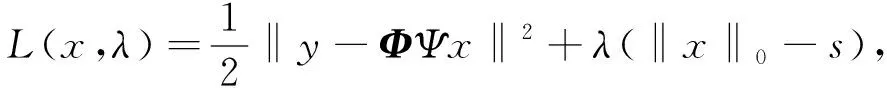
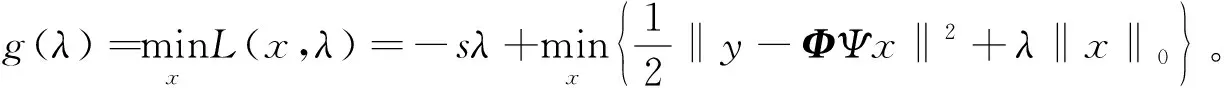
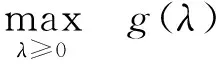
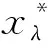


1.2 硬阈值迭代算法


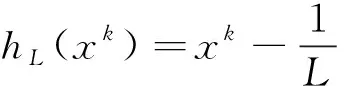
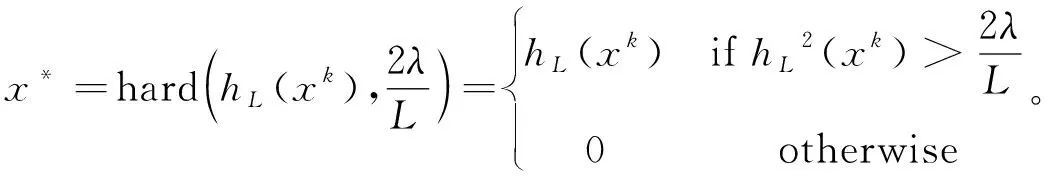

2 基于拉格朗日方法的图像恢复算法
3 实验

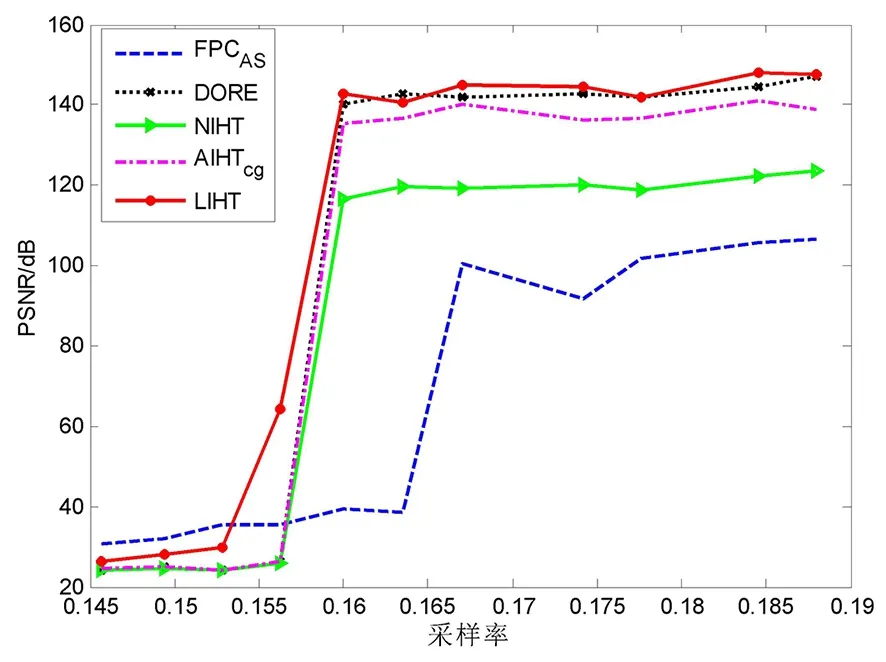
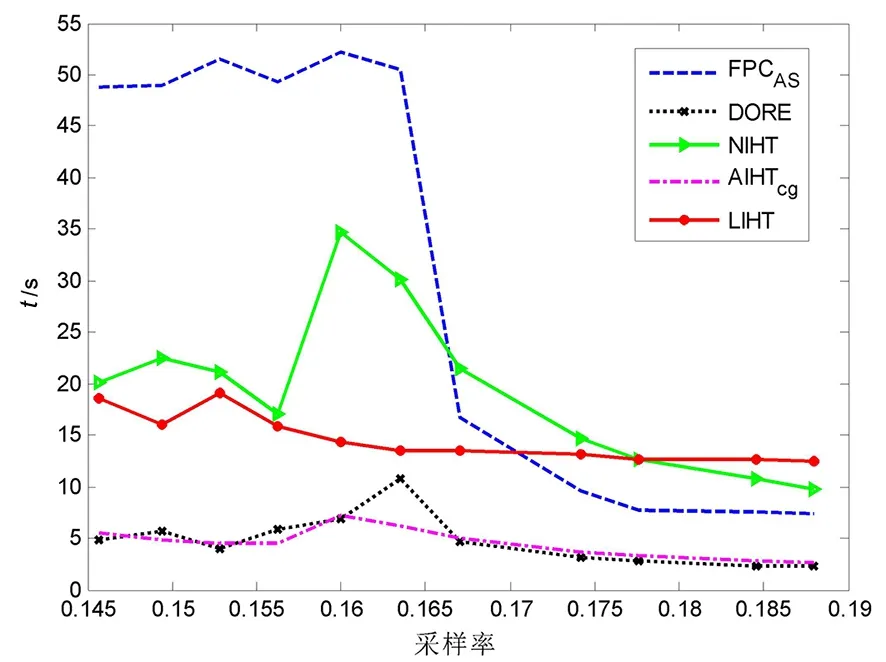
4 结语
