局部约束阻尼开口柱壳的减振分析及优化

赵冬艳， 王怿磊， 石慧荣

(兰州交通大学 机电工程学院，兰州 730070)

1 引 言

由于航空航天、潜艇、铁道车辆和船舶等工业领域中经常使用柱壳结构作为蒙皮或幕墙，而且柱壳壁厚相对较小，受外界激励会出现噪声和振动问题，而局部约束阻尼可以在引入较小质量的情况下达到较好的减振效果，因此也广泛应用于薄壁柱壳结的减振中。

使用粘弹性层耗散结构振动能量的约束阻尼减振在20世纪50年代已有应用，早期Kerwin等[1]主要针对板梁结构的约束阻尼减振。随着薄壁柱壳的广泛应用，约束阻尼柱壳的减振研究也受到很多学者的关注[2-4]。Mahmoudkhani等[5]应用Donnell壳理论和一阶剪切变形理论研究了由温升和空气静载荷引起预应力约束阻尼柱壳的振动特性。Mokhtari等[6]基于Donnell-Moshtari壳理论和Lagrange方程建立了含分数阶粘弹性芯层的约束阻尼柱壳模型，分析了结构参数、分数阶参数和耗散模量对振动频率和损耗因子的影响。郑玲等[7]采用局部敷设ACLD的方法，讨论了不同敷设位置对于振动特性的影响。一些学者对开口柱壳的动态特性进行了研究，Wang等[8]基于Pasternak基获取了厚壁开口柱壳的具有广义边界条件的三维精确解，并在ABAQUS中验证了该方法的准确性和可靠性。Karlash[9]对开口和封闭压电陶瓷柱壳进行了实验测试，表明相对开口柱壳，封闭柱壳共振模态的机电耦合系更大。

为了获得较好的减振效果，缩减约束阻尼结构质量，很多学者也对柱壳的约束阻尼设置进行了优化研究。Mohammadi等[10]利用遗传算法和二次规划方法对局部约束阻尼敷设位置、约束层和芯层厚度进行了优化。但基于某单一性能指标的结构优化，并不能满足工程实际中多模态减振问题[11]。石慧荣等[12]对分段敷设约束阻尼结构进行了多目标优化，从而在引入较小质量的条件下有效缩减了多个模态的振动。Li等[13]利用多目标粒子群优化算法对柱壳敷设压电层位置进行了优化，分析表明优化后的主动减振效果良好。袁维东等[14]对复合阻尼柱壳的多模态振动问题进行了拓扑优化，使敷设体积缩减为全覆盖的50%时仍然具有良好减振效果。

综上所述，目前主要是针对于整体圆柱壳模型进行振动分析及优化，而工程应用中局部开口柱壳结构应用非常广泛，其连接状态使得振动特性与整体柱壳存在较大差异，因此对局部约束阻尼开口柱壳的减振特性还有待进一步的深入分析。本文基于Sanders壳体理论和Lagrange方程建立了局部约束层阻尼开口柱壳动力学模型，对影响结构振动的主要因素进行分析，为了有效缩减开口柱壳的前三阶模态振动，利用 NSGA-II多目标优化算法对引入的约束阻尼结构进行优化设计，并对裸壳和优化前后约束阻尼结构柱壳的动态特性进行了比较分析。

2 局部约束阻尼开口柱壳动力学模型

局部约束阻尼柱壳由基层、阻尼层和约束层组成，结构如图1所示。R为基层半径，l为长度，hc为基层厚度；hv为阻尼层厚度，lv为阻尼单元长度，对应的敷设角为αv，粘弹性层沿轴向和周向均匀相间布置；hp为约束层厚度，αp为约束层敷设角；柱坐标系原点位于基层的中面上，x为柱壳的轴向，y为柱壳的周向，z为柱壳的径向，下标p，v和c分别为约束层、阻尼层和基层。

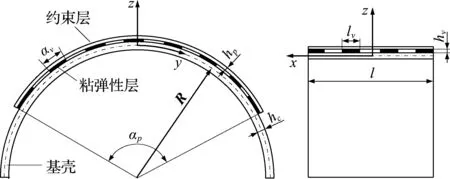
图1 局部约束阻尼开口柱壳模型

假定各层之间理想粘接，无相对滑动，采用Sanders壳体理论表示应力和位移之间的关系[15]，该理论能更准确地计算开口柱壳的固有频率，此时位移场可以表示为

u(x,y,z,t)=u0(x,y,t)+zβx(x,y,t)

(1a)

v(x,y,z,t)=v0(x,y,t)+zβy(x,y,t)

(1b)

w(x,y,z,t)=w0(x,y,t)

(1c)

式中u，v和w为复合圆柱壳在x，y和z方向的位移矢量，对应的基层中性面位移矢量用u0，v0和w0表示，矢量βy和βx为绕x和y轴的横向变形，z为位移变换矩阵，各矢量和矩阵可表示为

(2)

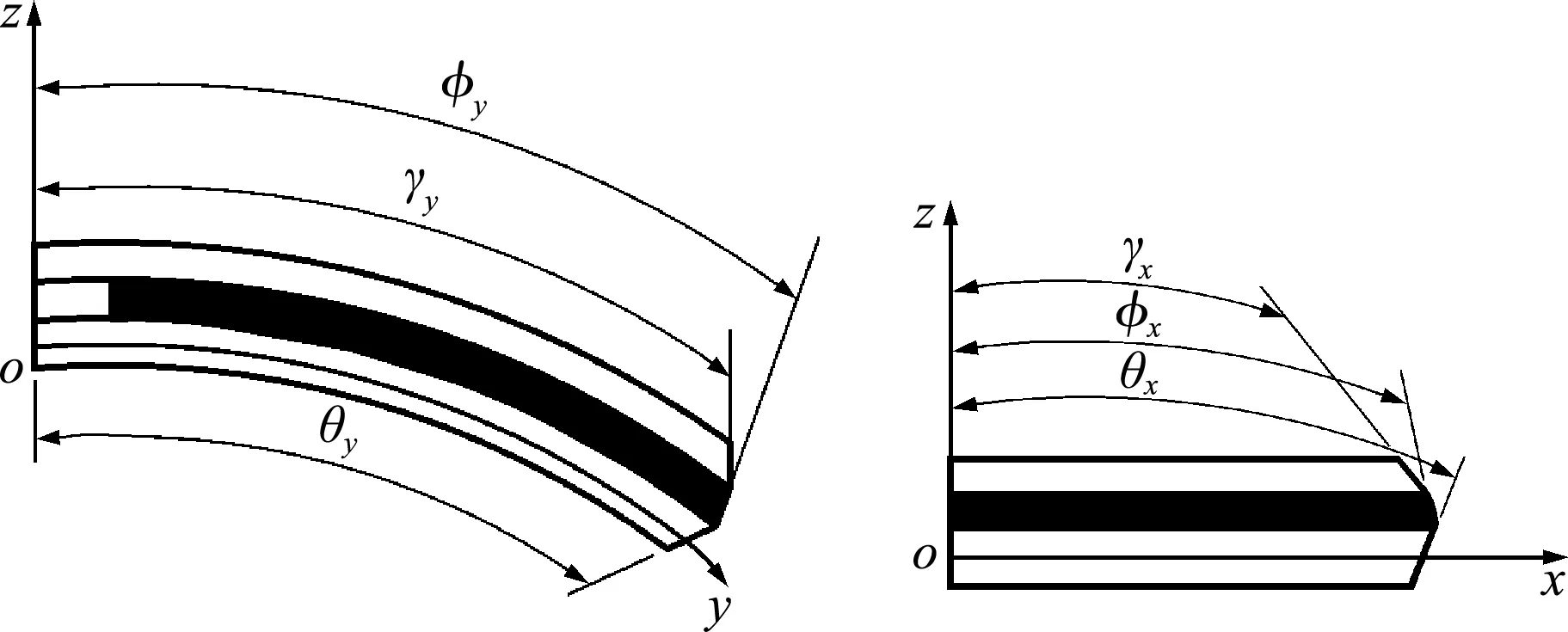
图2 各层扭转变形

2.1 应变-位移关系

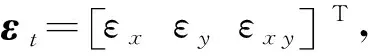
(3)

根据Sanders理论，基层、阻尼层和约束层的应变-位移关系表示为

εi=εt i+Zr iεr i

(4)

式中Zr为应变变换矩阵，下标i=(c，v，p)，εt，εr和Zr的具体形式如下，

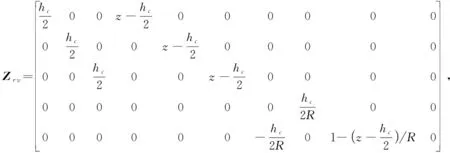
2.2 本构方程

(5)

则各层的应力可表示为

σi=Qiεi

(6)

式中Qi为刚度矩阵，可表示为

(7)

本文忽略各层纤维角的影响，根据文献[16]，对于各向异性的Qi j可表示为

(8a)

各向同性时可以表示为

(8b)

2.3 边界条件

对于约束阻尼开口柱壳的膜应力N和弯曲应力M向量，根据文献[17]可以表示为

Ni=Bi·εt i，Mi=Ji·εr i

(9)

则各层的膜应力和弯曲应力向量形式为

(10a)

(10b)

式中膜应力变换矩阵Bi和弯曲应力变换矩阵Ji分别为

(11)

本文对于基层柱壳的周向两端采用简支边界条件，根据简支边界条件有

约束层和阻尼层无约束，则有

2.4 位移形函数

根据Galerkin法，位移可表示为

U=Φq

(12)

式中Φ为结构形函数矩阵，q为广义结构坐标系，分别为

(13a)

(13b)

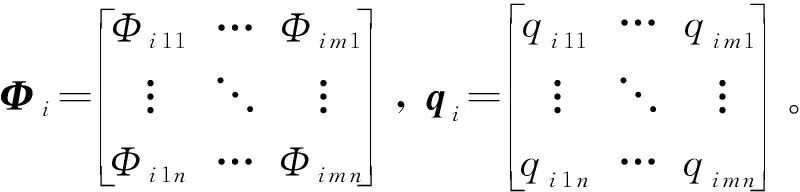
式中m为柱壳周向波数，n为柱壳轴向的半波数，i=u，v，w，θx，θy，Φx，Φy，γx，γy。

将式(13)代入应变-位移关系(4)，可得各层的应变为

εt=ni·q

(14)

式中ni的具体形式如下：

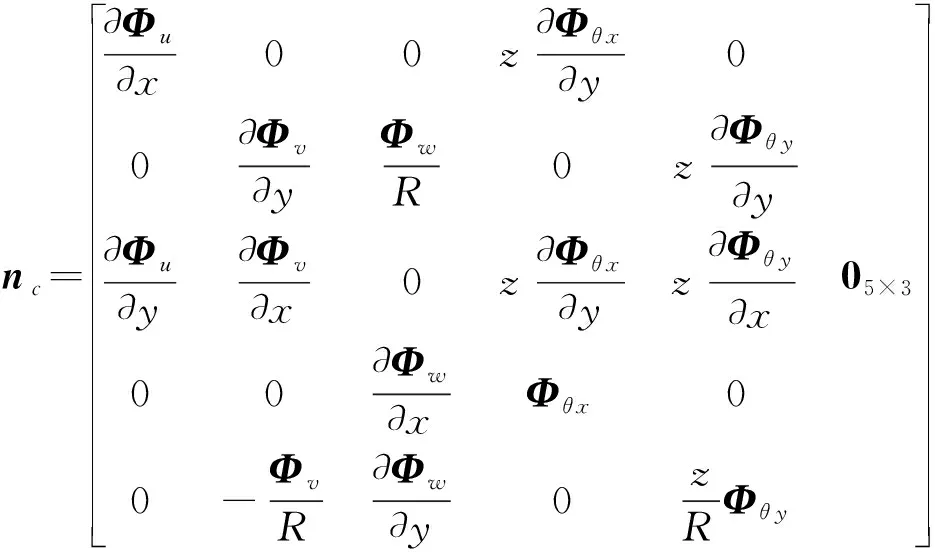
式中0为零矩阵。

由于柱壳绕x轴和y轴转动变形较小，因此忽略其对系统动能的影响，根据虚功原理以及能量法，约束阻尼柱壳结构的动能T可表示为

(15)

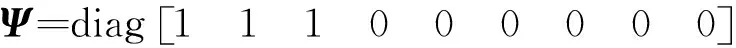
(16)

系统的总势能U可表示为

(17)

H*(xi,yi)=[H(x-xi 2)-H(x-xi 1)]·

[H(y-yi 2)-H(y-yi 1)]

(18)

式中H为Heaviside函数。

根据Lagrange方程，

(19)

式中W为外力做功，L=T-U，Fe为外加载荷。将式(15，17)代入方程(19)，可得系统的动力学方程为

(20a)

M=Mc+Mv+Mp，K=K1+K2+K3

(20b)

式中Mc，Mv和Mp分别为各层的质量矩阵，K1～K3为系统的刚度子矩阵，具体形式为

(21)

3 约束阻尼开口柱壳分析参数

3.1 模态损耗因子

根据式(17)可以获得各层的应变能，依据模态应变能法，第k阶模态损耗因子可表示为

通过设置紧急切断阀和SIS，不但实现了进、出口阀门的远程控制，而且增加了安全联锁保护措施，提高了罐区的安全性能，符合国家安全监管相关要求。

(22)

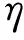
(23)

3.2 引入约束阻尼结构质量比

对于敷设约束阻尼结构而引入的质量MCLD=Mv+Mp太多会影响开口柱壳应用特性，本文定义MCLD与基壳质量Mb的比值为

∈M=MCLD/Mb

(24)

式中Mv和Mp分别为粘弹性层和约束层的质量。为了减小结构振动，在考虑损耗因子最大化的基础上，不能引入太大的质量。

3.3 阻尼层占空比

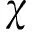
(25)

4 约束阻尼开口柱壳振动影响因素

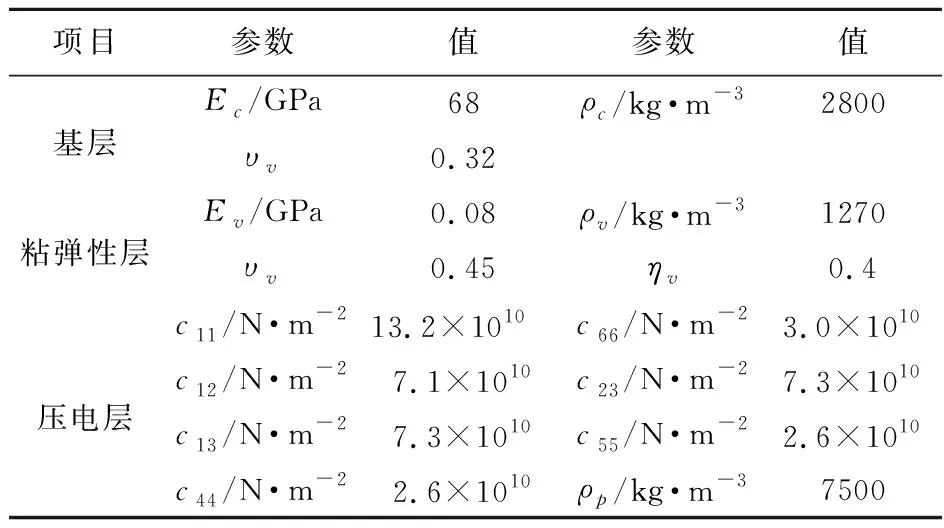
表1 各层材料属性

4.1 粘弹性单元分段数

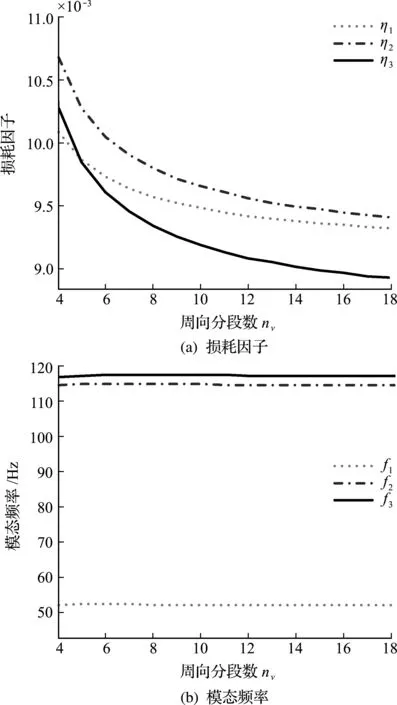
图3 周向分段数对损耗因子和模态频率的影响

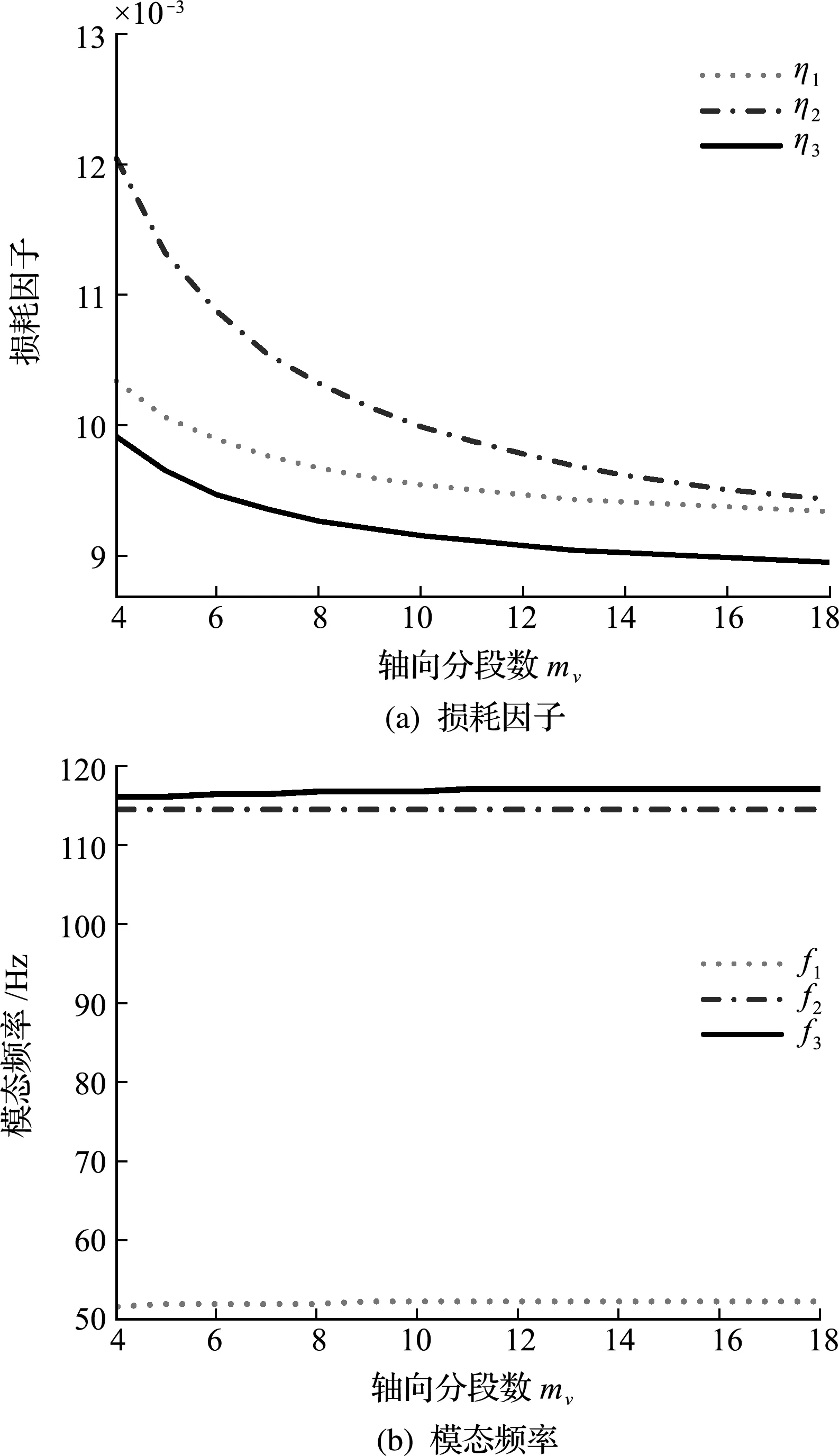
图4 轴向分段数对损耗因子和模态频率的影响

可以看出，其他不变时，阻尼单元分段数的增加会导致阻尼层敷设面积减小，使得开口柱壳变形时阻尼结构耗散的能量减小，损耗因子减小，但也注意到各模态形变不同，所以在分析中表现出阻尼分段数对变形较大的第二阶模态损耗因子影响较大。因此，选取阻尼单元分段数时，要根据结构的实际应用确定，保证柱壳具有良好的减振特性。

4.2 粘弹性层厚度

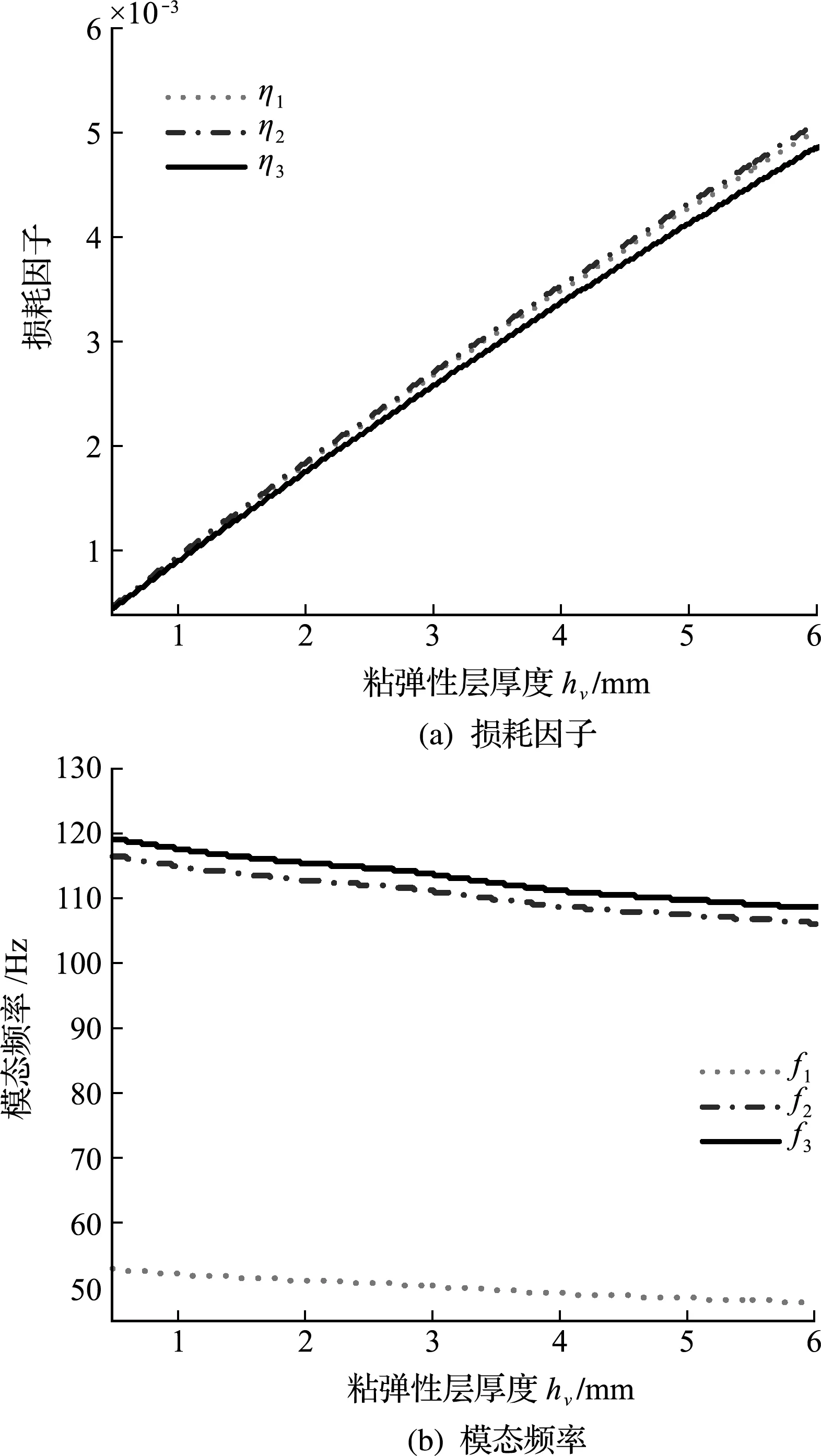
图5 粘弹性层厚度对损耗因子和模态频率的影响

4.3 约束层厚度

4.4 粘弹性单元占空比

4.5 约束层敷设角

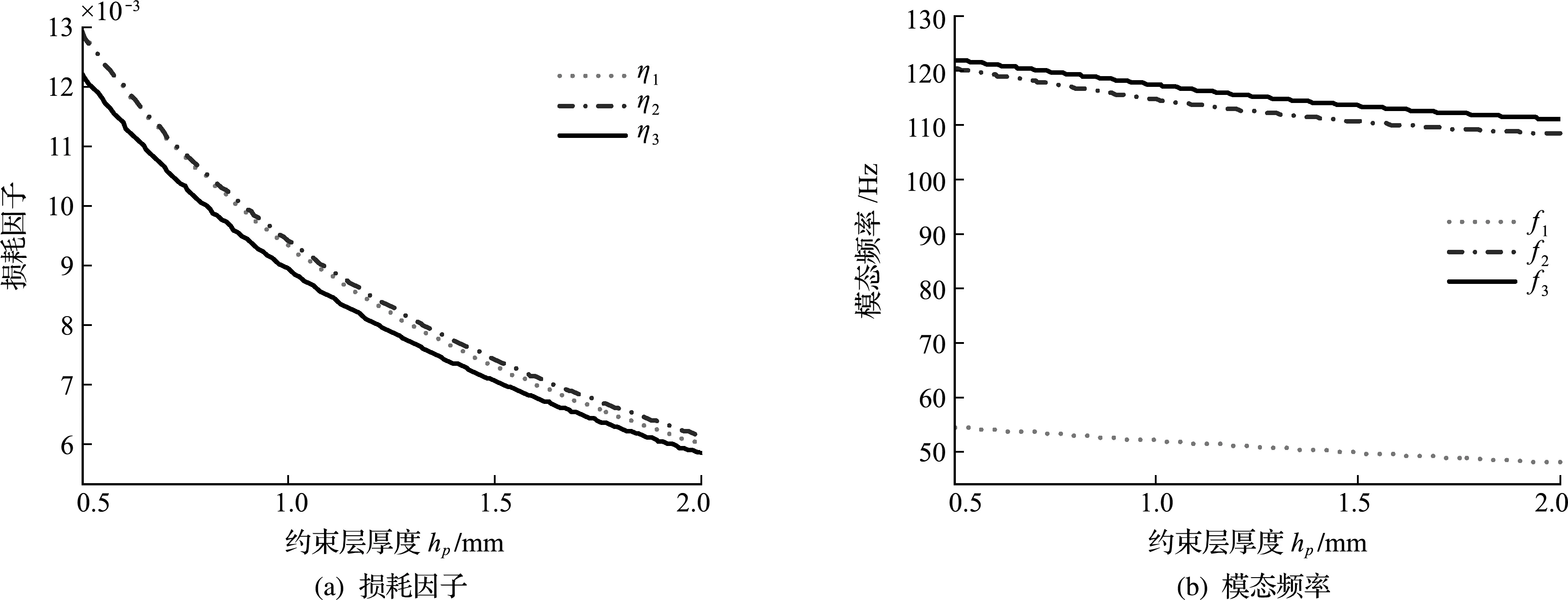
图6 约束层厚度对损耗因子和模态频率的影响

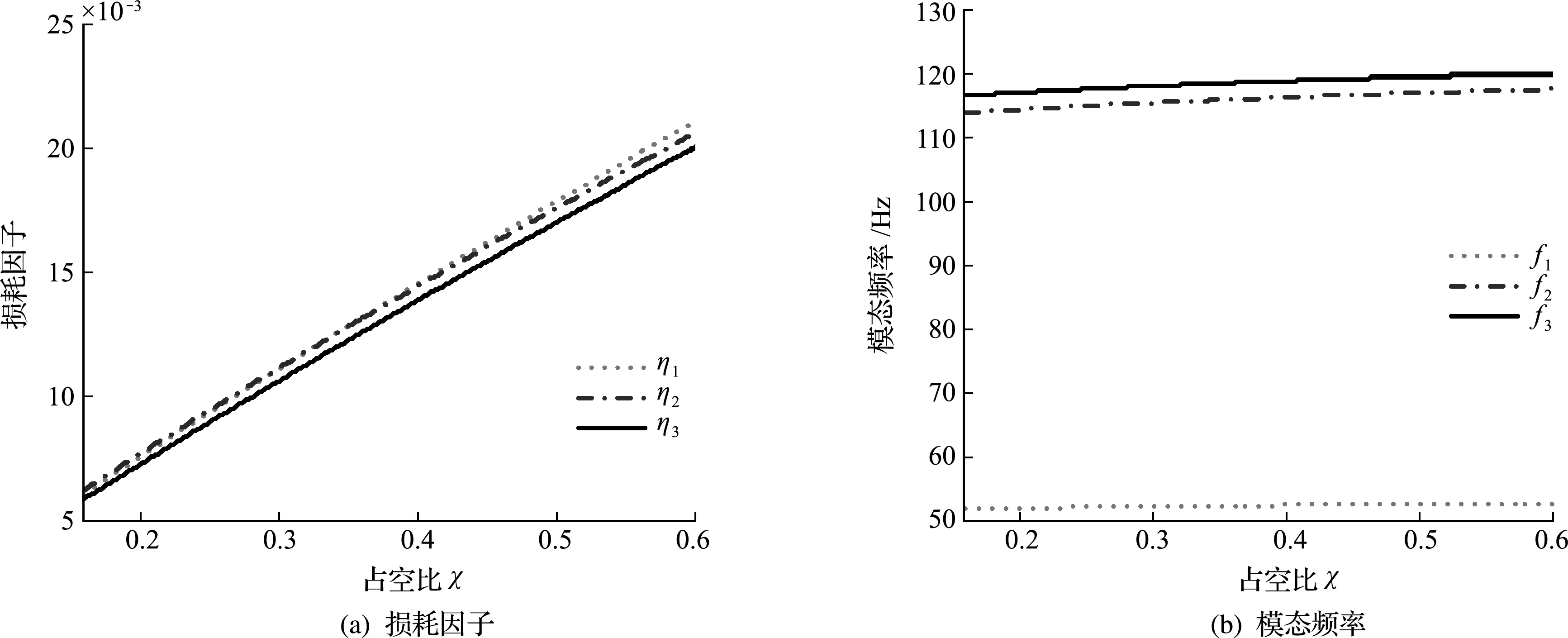
图7 占空比对损耗因子和模态频率的影响

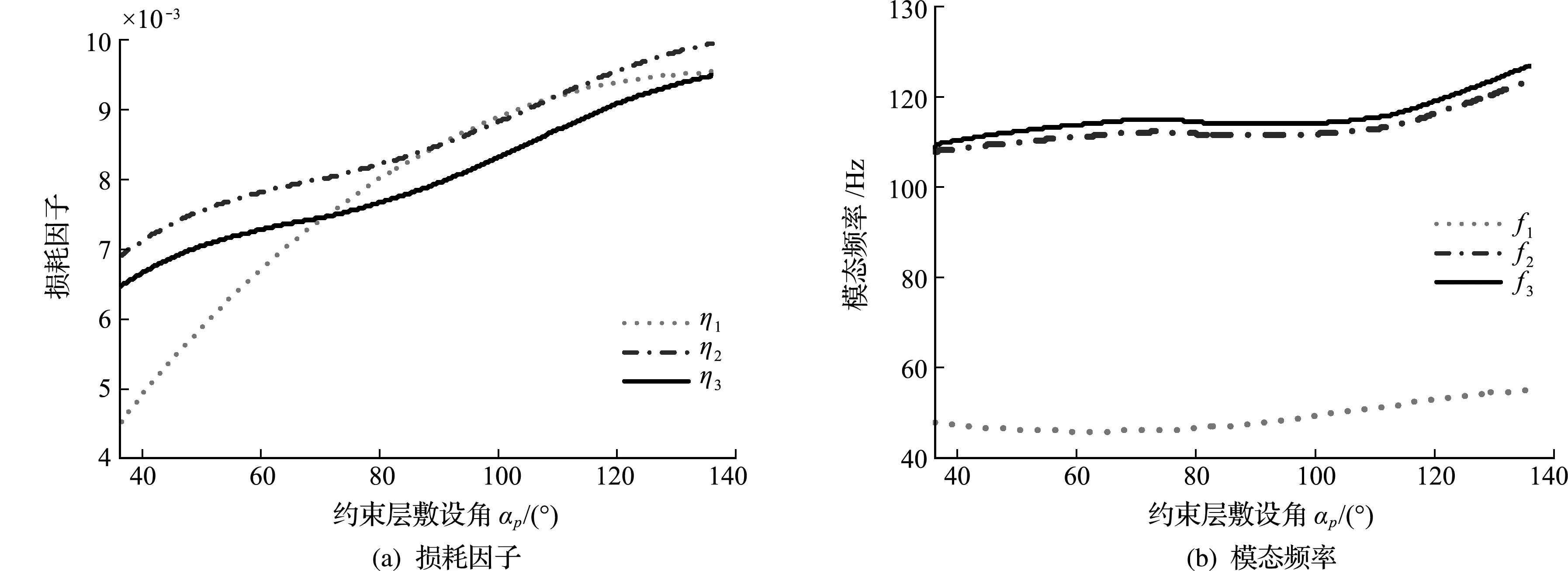
图8 约束层敷设角对损耗因子和模态频率的影响

5 结构优化设计

5.1 NSGA-II优化算法

针对开口约束阻尼柱壳，本文利用基于Pareto最优的NSGA-II多目标优化法对结构进行优化设计[18]。NSGA-II优化算法可以随机产生多种初始种群，对其进行非支配排序，然后利用遗传算法的选择、交叉和变异得到第一代子代种群，第二代后，子代种群与父代种群合并，再次排序，并计算每个非支配层中个体的拥挤度，选取合适的个体组成新的父代种群，通过遗传算法产生新的子代种群，多次迭代后得到全局最优。

5.2 设计变量

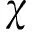
(26)

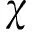
5.3 目标函数

为了满足多种工程实际应用要求，本文考虑缩减结构前三阶模态的振动，使引入约束阻尼结构在图3所示的三阶模态具有较大的能量耗散，获得较好的综合减振性能，因此将前三阶模态损耗因子作为目标函数，通过优化计算使其最大，则可以设定目标函数F(·) 为

(27)

式中gi(·)为损耗因子函数，下标i=1，2，3，此时使F(·)最小化，得到的开口约束阻尼柱壳的损耗因子最大。

5.4 优化结果分析

5.4.1 优化结果

对于约束层阻尼开口柱壳的多目标优化，转变为一般的极小值问题minF(·)，可得到如图9所示的Pareto最优解集。可以看出，在可行解集中，Pareto最优解不唯一，各最优解之间也没有优劣之别，只是Pareto最优解所对应的个体性能更好。本文利用NSGA-II算法原理，能够将Pareto域的最优gi均匀地扩展到整个可行解集中，从而形成保持多样性的最优种群，选择参加繁殖的gi产生的后代同其父代个体共同竞争来产生下一代种群，使存留gi保持更好的优良性，由此获取的最优解能够更好地满足约束阻尼开口柱壳的应用特性。

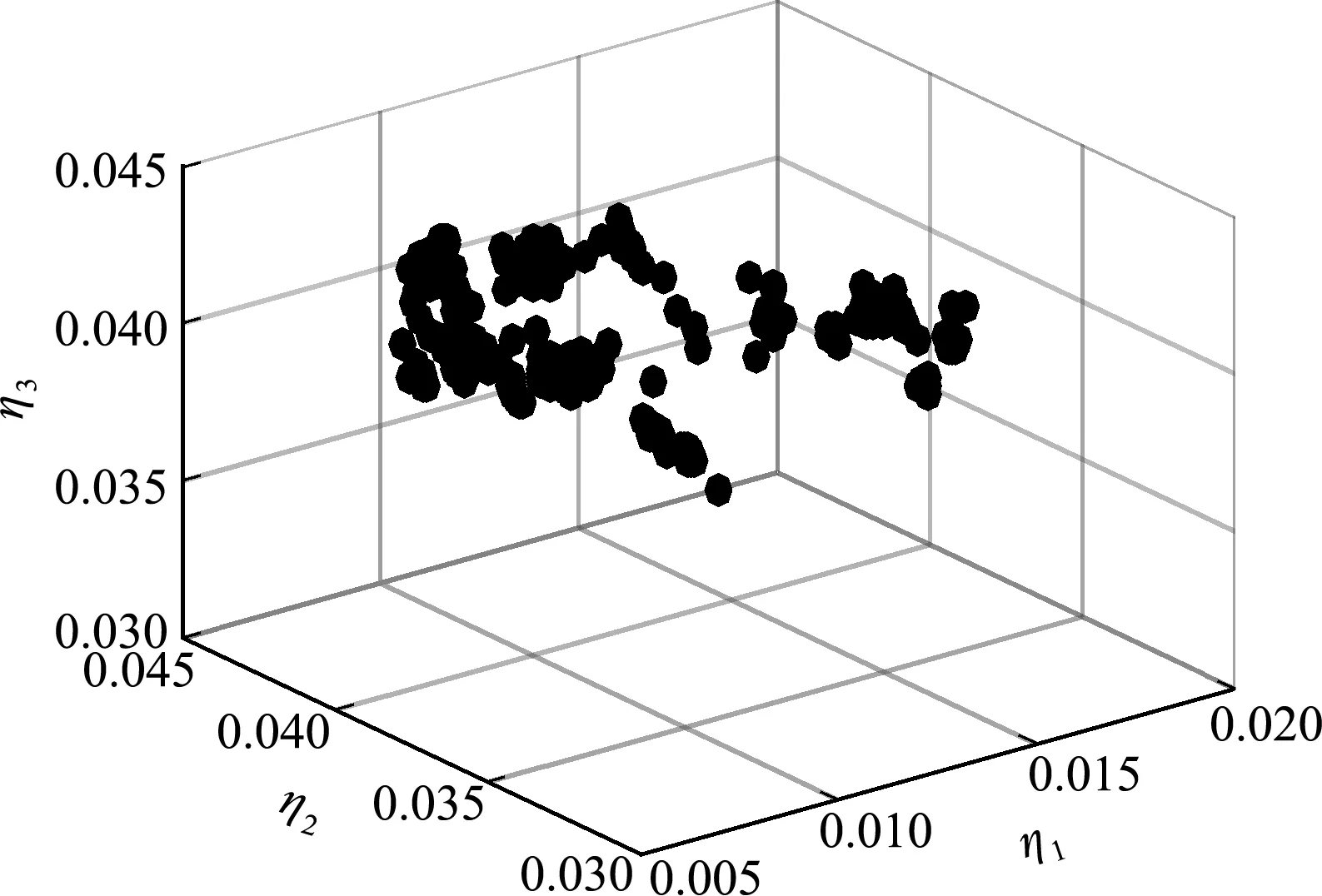
图9 Pareto前沿

由表2优化前后的设计结果可以看出，优化后结构相对于优化前约束阻尼结构质量比∈M由 90.33% 减小到了37.8%，有效缩减了系统质量，此时引入的约束阻尼可以有效耗散系统振动能量，使得结构的前三阶模态损耗因子都显著增加，其中第二阶模态柱壳周向中部变形最大，因此损耗因子增幅也最大；而且也可以看出，虽然优化后的结构敷设角αp减小了约36°，阻尼层和约束层厚度都有所减小，但合理选取粘弹性单元分段数和占空比，能够在引入较小阻尼结构质量的条件下，进一步使开口柱壳结构具有良好的减振性能。

表2 优化前后参数

5.4.2 优化前后动态特性分析

图10是优化前后柱壳中点施加100 N径向简谐作用力后得到的频率响应曲线。

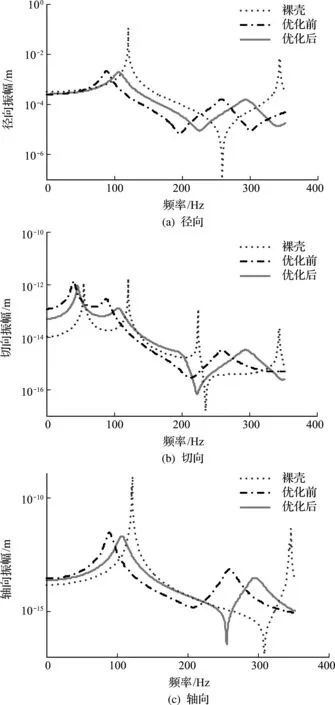
图11 开口柱壳频率响应曲线

可以看出，相对裸壳，敷设约束阻尼结构可有效减小前三阶模态幅值，优化结构幅值缩减更加显著，并且相对裸壳的模态频率变化更小。从图10(a)可以看出，在以径向振动为主的第二阶模态处，优化前的径向幅值 2.18×10-3m对应频率 88.2 Hz，优化后的模态频率为 107.2 Hz，峰值变为1.9×10-3m，较裸壳在第二阶模态 120.26 Hz 处的峰值0.114 m大幅缩减；图10(b)表明，优化结构对应的前三阶模态在切向的振动较优化前和裸壳均有所减小，但优化结构的切向振动缩减有限；图10(c)中，柱壳的最大轴向振动幅值出现在第三阶模态，优化结构的轴向振幅也相对较小。同时通过柱壳三个方向的振动响应可以看出，优化结构较裸壳模态频率变化更小，而且由表2知其引入质量仅为37.8%，因此优化结构可在引入较小阻尼结构质量条件下，在改变固有频率较小时有效缩减柱壳振动，因此更加有利于实际应用需求。

6 结 论

通过对影响模态频率和损耗因子参数的分析和对约束阻尼开口柱壳进行结构的NSGA-II优化，可以得到以下一些结论。

(1) 根据Lagrange方程以及Sanders壳体理论能够准确建立局部约束阻尼柱壳模型。

(2) 增加阻尼单元周向与轴向分段数和约束层厚度，损耗因子减小；增大约束层敷设角、阻尼单元占空比和阻尼层厚度可以增加结构的损耗因子；粘弹性层和约束层厚度越大，模态频率下降越多，占空比增加，模态频率也随之增大，阻尼单元分度数对模态频率几乎无影响。

(3) 利用NSGA-II法对约束阻尼结构进行优化，能够在大幅缩减约束阻尼结构引入质量的情况下，有效抑制开口柱壳结构的振动。