基于OpenSees的铁路高墩桥梁弹塑性地震响应研究

赵海青

(中铁二十局集团有限公司 陕西西安 710016)

1 引言

在山岭地区修建铁路，受到地形起伏的变化，铁路线路不可避免地需要跨越山谷、丘壑、河流、障碍物等，以克服高程差异以及缩短线路和改善线型等，桥梁高度一般达到几十米至百米以上不等[1-2]。这些高大桥墩在强震作用下受到的破坏比一般中低高度的桥梁大，这是因为桥墩具有高度大、自重大和柔性大的特点，在受到地震荷载时发生空间多维振动变形，呈现明显的空间特性[3]。目前，高墩桥梁抗震设计理论和方法缺乏足够的技术储备，现行规范主要适用于中低高度桥墩，它无法提供详细的高大桥墩的设计指导[4]。高大桥墩抗震设计时，无法简单地参考现行规范，因此，亟待开展相关研究工作[5]。此外，由于桥梁跨度不断增加，减隔震技术应运而生，其不仅能提高桥梁抗震性能，还能降低工程造价。由于高速铁路桥梁中高速列车对结构横向刚度存在较高要求，使得减隔震技术在铁路桥梁中的应用仍处于探索阶段[6-7]。因此，研究带有减隔震装置的高墩地震响应，对于指导强震区铁路桥梁抗震设计具有重要的现实意义[8]。

以新建铁路宝鸡至兰州客运专线新店子特大桥为研究对象，基于OpenSees软件运用IDA增量动力分析法进行结构弹塑性地震响应分析，研究安装减隔震装置的重力式变截面铁路高墩桥梁的地震响应特征，分析墩高与弯曲系数的相关关系。研究成果可应用于高大铁路桥墩的抗震分析。

2 弹塑性纤维梁柱单元

计算时，采用开放体系地震工程模拟程序OpenSees程序进行动力学模拟，运用弹塑性纤维梁柱单元将单元截面离散成纤维，对于不同位置的纤维赋于相应的材料属性，服从非线性应力-应变关系，在不考虑剪切变形条件下，假设纤维之间完全黏结且满足平截面假定，扭转刚度则采用与弯矩、轴力均不耦合的弹性扭转理论进行确定[9]。

目前，较成熟可靠、计算高效的纤维梁柱单元是基于柔度法的弹塑性纤维梁柱单元。柔度法将力作为未知量，采用力插值函数建立单元的柔度矩阵，以此计算单元的内力和变形。对于假定的内力分布，无论单元及纤维处于何种状态，基于柔度法的弹塑性纤维梁柱单元都能严格满足平衡条件，能够更真实地反映结构中内力与变形的分布，不受单元材料非线性水平的影响和制约[10]。

3 弹塑性动力分析

3.1 工程概况及计算模型的建立

新建铁路宝鸡至兰州客运专线东起陕西省宝鸡市，沿渭河峡谷进入甘肃省天水市。新店子特大桥位于甘肃省通渭县境内，全长4 199.92 m，共129跨，基础桩1 096根，总长41 854延米，是宝兰客专甘肃段8标管段内最长的桥，主线桥桥跨布置为119×32 m＋3×24 m＋5×32 m＋1×24 m＋1×32 m简支梁桥，墩高变化从7.00～31.00 m不等，其中里程IDK873＋019.83～IDK872＋790.93段，墩高大于30 m，如图1所示。

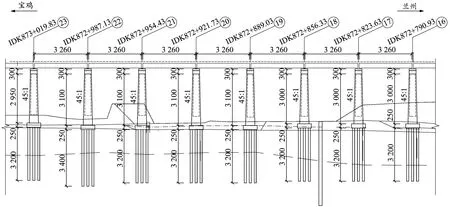
图1 桥梁剖面图

为分析高墩桥梁在地震作用下的响应特征，采用OpenSees程序进行时程分析时，需将桥墩进行简化，即将桥梁高墩理想化为单墩模型，墩支座上部的梁体简化为一个质量块，并采用零长度单元与墩顶连接，如图2所示。模型中设置零长度单元的原因是因为在支座位置处，桥墩结构设置了隔震支座，通过赋予零长度单元相应特性以达到模拟隔震支座的目的。模型边界条件设置为墩顶上部质量块边界自由，墩的底部边界条件设为固结。

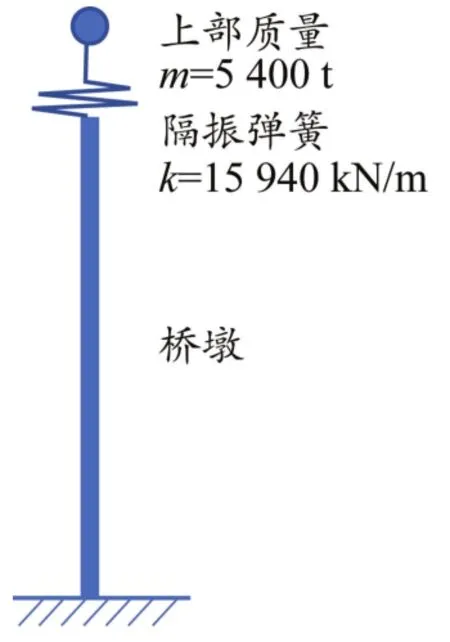
图2 桥梁高墩计算模型

模型建立时，筋纤维采用考虑包辛格效应和硬化阶段修正的Menegotto-Pinto本构模型，混凝土纤维采用考虑箍筋对核心混凝土约束效果的Mander本构模型。建立不同墩高的桥墩动力模型，计算结构弹塑性地震响应，墩高分别设置为30 m、28 m、24 m和20 m，以研究不同墩高铁路桥梁弹塑性地震响应行为及其差异性。

3.2 截面屈服曲率的确定

截面屈服曲率是模型计算的必输入参数，而截面屈服曲率φy与截面承受轴力大小有关。结构承受地震作用时不同截面处轴力响应值随时间变化，因此，精确分析结构各截面不同时刻屈服曲率所需计算量较大，为简化分析，忽略动轴力，对截面施加恒载轴力计算屈服曲率，屈服曲率φy与桥墩高度h的关系曲线如图3所示，其中墩底与墩顶位置分别对应于图中高度h＝0 m与h＝30 m，当桥墩截面地震曲率响应值超过该处屈服曲率时认为该截面达到屈服。

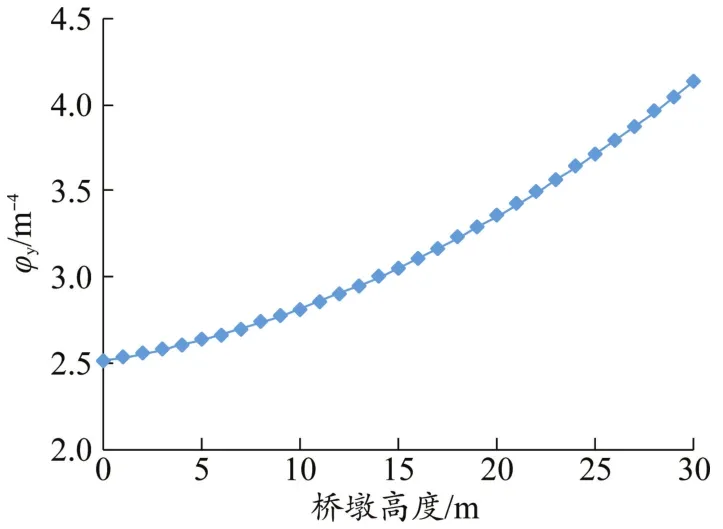
图3 截面屈服曲率确定

3.3 模型的正确性验证

由于OpenSees程序没有可视化建模功能，用户无法直观判断各纤维单元是否处于截面中的正确位置，以及模型约束条件是否和预期相同。为此，采用商用可视化有限元软件平行建模对比分析，验证OpenSees程序模型几何参数、边界条件、计算结果的正确性。建模时，由于商用可视化有限元软件无法建立符合本算例中的非线性模型，因此，将OpenSees程序中纤维模型的材料本构改为线弹性本构，进行线弹性有限元计算。在有限元模型中，采用35个等截面柱近似模拟实际的变截面墩结构，在桥墩顶部添加一个模拟主梁的质量点，该质量点通过弹簧单元与墩顶节点连接，弹簧单元用于模拟隔震支座，边界条件与OpenSees程序模型一致。表1为两个软件模型的前3阶自振频率对比结果。从表1中可以看出，OpenSees程序与商用可视化有限元软件关于桥梁高墩自振特性的计算结果基本一致，验证了OpenSees模型的正确性。

表1 自振频率 rad/s

3.4 塑性铰区的扩展过程分析

为使桥墩更多截面屈服以便观察塑性铰区的扩展过程，选择地震动加速度PGA＝0.49 g进行地震动时程曲线分析。由此得到不同墩高的桥墩塑性铰区域形成和发展过程，如图4所示，图中纵坐标表示桥墩高度h，横坐标为时间t，圆圈标出部分为截面屈服产生的塑性铰区。

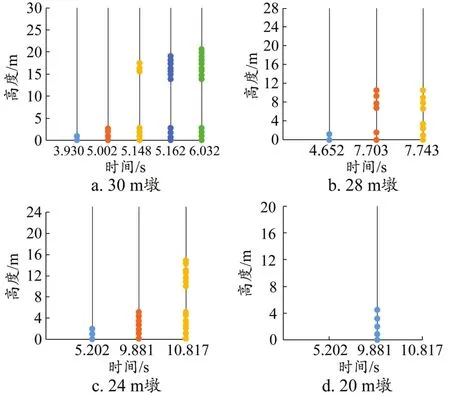
图4 塑性铰发展过程

从图4中可以看出，桥墩为30 m时，塑性铰区首先出现在墩底，并逐渐向上部延伸扩展至大约1 m长，随后在距墩底15.5 m位置出现第二个塑性铰区并分别向墩底和墩顶扩展，第二个塑性铰区长度扩展至大约6.7 m之后停止；桥墩高度为28 m时，桥墩首先在底部出现塑性铰区并扩展至大约1.2 m，随后在距墩底约6.8 m处出现第二个塑性铰区；桥墩高度为24 m时，第一个塑性铰区首先在墩底出现并扩展到大约5.0 m后停止，随后在距离墩底大约10.0 m处出现第二个塑性铰区；桥墩高度为20 m时，塑性铰区出现在墩底，并扩展至大约4.4 m，直至激励结束时桥墩没有出现第二个塑性铰区。

由图4可知，铁路桥梁20 m及以上高墩在地震作用下可能产生多个塑性铰区，而20 m以下的中墩及矮墩在地震作用下仅出现一个塑性铰，通过该现象分析，高墩桥梁比矮墩桥梁的高阶振型效应对结构地震响应贡献显著增大。因此，对于铁路中高墩桥梁的抗震设计，有必要开展弹塑性分析以确定潜在塑性铰区的具体位置和长度，强化该区域箍筋的加密配置等构造措施，以便提高塑性铰区的延性变形能力，防止结构脆性破坏。

3.5 墩顶位移IDA分析

增量动力分析(IDA)是用于评价结构抗震性能的一种动力参数分析方法，通过对结构施加一个地震动记录，采用不同的比例系数将此地震动记录进行调整获得一组不同强度的地震动输入，运用这组地震动输入对结构进行非线性时程分析，最后绘制结构性能参数(如墩顶位移、墩底曲率)与地面运动参数(如地面峰值加速度)的关系曲线，即IDA曲线，以达到研究地震作用下结构物的损害破坏全过程。

桥墩的位移是衡量桥墩延性的重要指标。应用增量动力分析方法，不断增大峰值加速度，直至计算桥墩位移不收敛则认为结构破坏并达到极限位移，得到墩顶和墩底的位移与地震峰值加速度关系如图5所示。

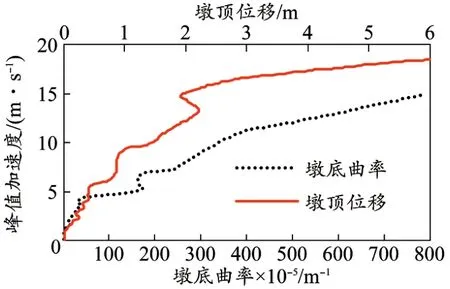
图5 桥墩位移与峰值加速度关系曲线

由图5可知，墩顶位移达到2.07 m、墩底曲率达到163.5×10-5m-1后均迅速增大，直至达到极限值。

应用OpenSees程序、商用可视化有限元软件分别对30 m桥墩极限位移与墩底截面极限曲率进行计算，并与《公路桥梁抗震设计细则》的规定方法计算进行比较[11-12]，对比结果如表2所示。由表2可知，针对所计算的30 m高墩，按商用可视化有限元软件计算得到的极限曲率(屈服位移)比OpenSees程序非线性计算得到的极限曲率(屈服位移)要大，按规范计算得到的极限位移远小于非线性计算得到的极限位移。因此，按规范计算是偏于安全的，墩顶位移达到规范计算的极限值后仍有很大变形能力。

表2 30 m桥墩计算结果对比

4 单向激励作用下的双弯曲现象

针对本文所分析的桥墩，当沿着截面z方向施加地震激励(PGA＝0.33 g)时，墩柱不仅在z方向产生弯矩响应，在y方向也产生弯矩响应，即产生了奇怪的“双弯曲”现象，这点与传统概念中的单向激励下单向弯曲现象完全不同。

4.1 双弯曲现象的验证

对有限元模型分别输入两个方向的激励进行计算，如图6所示，得到墩顶位移时程如图7所示。

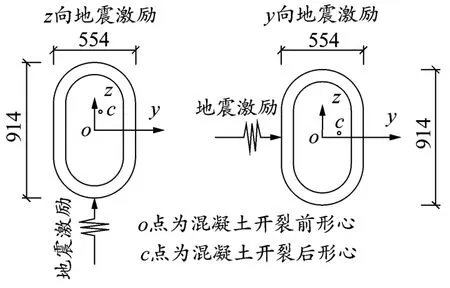
图6 地震激励方及截面形心偏移

从图7中可以看出，采用有限元软件进行非线性分析，在z方向和y方向地震激励作用下，桥墩均产生双弯曲现象。

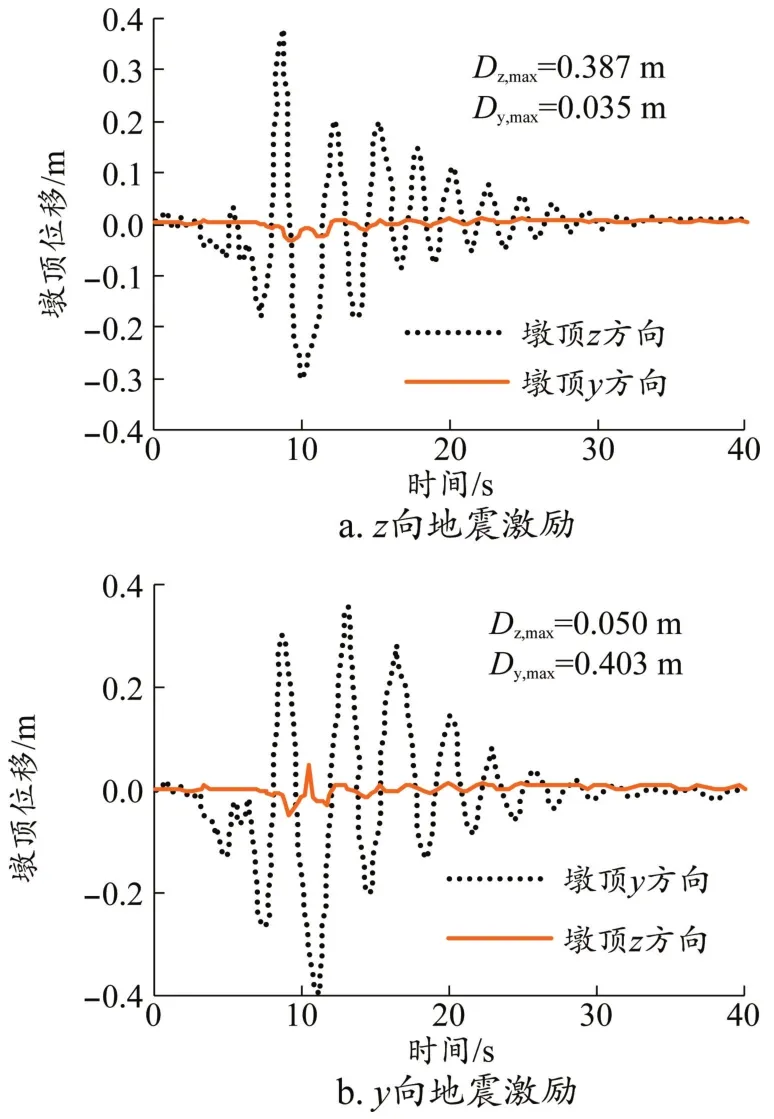
图7 有限元软件非线性计算结果

4.2 双弯曲现象的机理

推测单向激励下的双弯曲现象是由于混凝土开裂导致截面形心偏移所造成。如图6所示，在地震荷载作用之前，假设截面的质心与截面的形心重合，即重力作用在截面形心。在z方向地震作用下，沿着z方向截面边缘混凝土首先开裂，由于两侧混凝土不对称开裂，导致开裂之后截面形心相对于原形心不仅有z方向偏移，还有y方向偏移，但总体而言，z方向的形心偏移量远大于y方向。以此类推，地震激励方向为y方向时，具有类似规律。混凝土开裂之后虽退出工作，但其质量仍对结构产生影响，因此轴向力(包括重力、绝对惯性力与阻尼力)仍作用在截面原形心，从而使得轴向力对开裂后的截面产生了附加弯矩，即形心沿着z和y方向的偏移使得轴向力分别产生附加弯矩MGy和MGz，导致了单向激励下“双弯曲现象”的产生。

根据上述解释可知:双弯曲现象是由于混凝土的不对称开裂导致截面形心在垂直于激励方向产生偏移，从而使得轴向力产生了垂直于激励方向的附加弯矩所致，如混凝土不发生开裂则无双弯曲现象。

为了验证以上推测，在OpenSees模型中将混凝土材料本构模型修改为线弹性本构，且控制混凝土不开裂，得到墩顶位移时程曲线如图8所示。

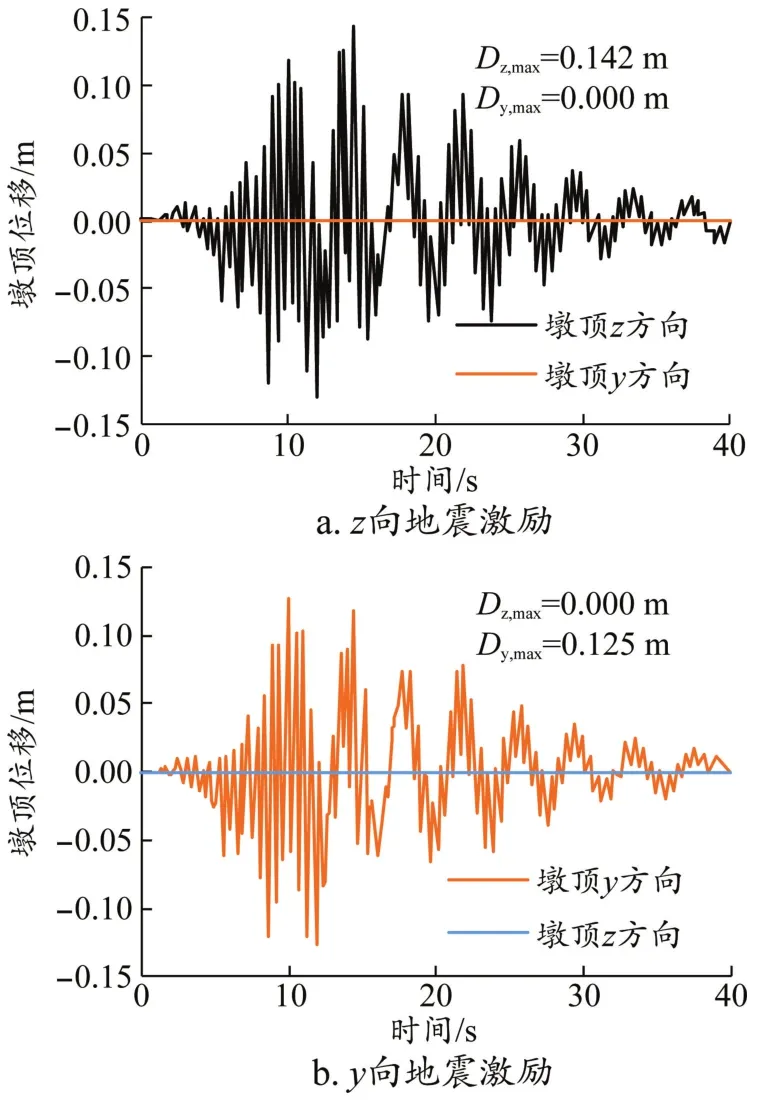
图8 OpenSees程序线性计算结果

线弹性计算结果进一步验证了上述推论，当混凝土采用线弹性本构模型而不使其发生开裂失效时，z向地震激励和y向地震激励均无双弯曲现象。

4.3 墩高和PGA对双弯曲现象的影响

基于所分析的桥墩在z方向地震激励作用下产生双弯曲现象，为反映两方向弯曲变形的相对大小，定义双弯曲系数η:

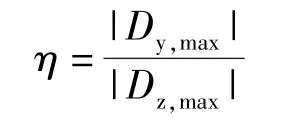
式中，Dy，max为墩顶y方向最大位移；Dz，max为墩顶z方向最大位移。

双弯曲系数是垂直于振动方向的最大墩顶位移绝对值与振动方向最大墩顶位移绝对值的比值，当双弯曲现象比较明显时η值较大，反之η较小。分别计算墩高为24 m、28 m和30 m的墩柱双弯曲系数随地面峰值加速度的关系，如图9所示。

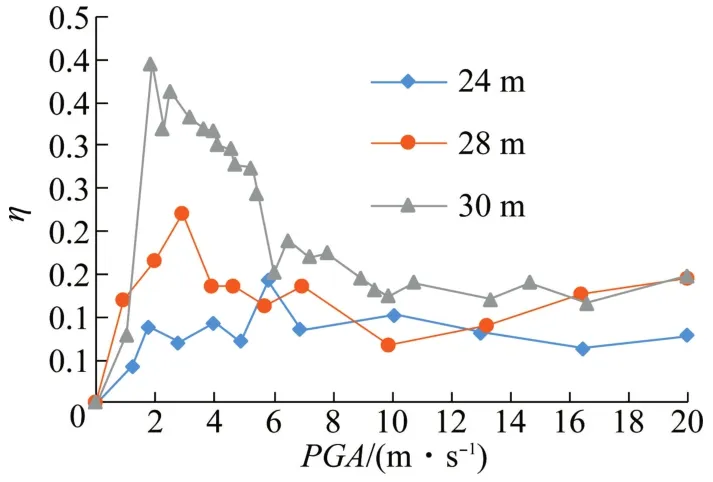
图9 PGA-η 曲线

由图9可知，双弯曲系数总体上随着墩高的减小而降低，随着PGA的增加先升高，达到峰值之后随着PGA的增加而降低。这可能是由于随着PGA增加截面混凝土的开裂程度加剧，使得形心偏移量增大，但当PGA达到一定数值之后截面已经充分开裂，垂直于振动方向附加弯矩增加速度减小，而在振动方向墩顶位移加速增大。

5 结论

以宝鸡至兰州客运专线新店子特大桥为研究对象，采用OpenSees程序建立模型进行非线性IDA分析，采用弹塑性纤维梁柱单元建立墩柱模型，考虑上部梁体重量及隔震支座的影响，进行地震响应分析。分析过程中考虑了不同墩高的影响，针对所分析的桥墩得出以下结论:

(1)高墩在地震激励作用下，除了会在墩底产生第一个塑性铰区之外，还可能在墩高中间位置产生第二个塑性铰区。因此对于高墩，有必要考虑第二个塑性铰区的影响，在对应区域采取如箍筋加密等构造措施，防止桥墩在第二个塑性铰区位置发生脆性破坏。

(2)当沿着一个方向对桥墩施加地震激励进行弹塑性分析时，由于混凝土不对称开裂造成形心在垂直于振动方向产生偏移，使得轴向荷载与竖向惯性力产生垂直于振动方向的附加弯矩，从而产生双弯曲现象。如采用弹性分析，由于桥墩截面重心和形心始终重合，不会产生双弯曲现象。

(3)对于出现双弯曲现象的截面墩，其弯曲系数η随着墩高降低而减小，随着PGA增加先增大后减小，出现一个峰值。但垂直于振动方向附加弯曲随着PGA增加而增大，这是由于PGA随着增大截面混凝土不对称开裂程度加剧，截面形心垂直于振动方向的偏移量持续增加所导致。