基于模态试验的某重型汽车驱动桥壳随机振动分析
2022-04-20孟红博郑忠才韩东越张一凡
孟红博,郑忠才,刘 娜,韩东越,张一凡,夏 群
(1.山东建筑大学机电工程学院,山东 济南 250101)(2.新泰市科学技术局,山东 新泰 271200)
汽车驱动桥壳作为汽车的主要承载件和传动件,在汽车上既是传动系统的一部分又是驱动系统的一部分, 驱动桥壳作为主减速器、差速器等零部件的保护装置,它与从动桥壳共同支承着车架和车身以及其他一些零部件的质量, 同时还承受着由驱动车轮与路面传来的反作用力和力矩。因此,驱动桥壳的好坏直接影响汽车的动力性能和安全性,从而影响燃油经济性。根据汽车设计理论,驱动桥壳的设计应该同时满足应力和应变的要求[1-2],为了在设计上满足驱动桥壳的强度和刚度要求,本文以驱动桥壳的模态分析为研究点,通过频率响应试验的数据与仿真数据的对比分析,展开对驱动桥壳的随机振动分析,从而证明驱动桥壳整体及部分结构的合理性以及在模拟仿真软件中数据分析的准确性。
1 驱动桥壳三维模型的建立
为了分析的合理性,在对驱动桥壳进行仿真分析之前,对桥壳进行简化。忽略掉螺纹孔、放油孔、圆角、倒角、焊接痕迹等非关键部件[3],仅对桥壳本体进行分析。本文针对某重型汽车后驱动桥壳进行建模分析,桥壳类型为整体冲焊式,在三维建模软件中对其进行建模,图1为驱动桥壳的实物图。

图1 驱动桥壳实物图
驱动桥壳总长L0=1 393 mm,板簧距L1=662 mm,壁厚T=12 mm,法拉盘直径d1=128 mm,法兰盘到桥壳中心距S=697 mm,后壳直径d2=110 mm。为了不影响后续的有限元仿真分析结果并使分析结果更加精确,在绘制三维模型之前需要精确地测量驱动桥壳的尺寸。在做完以上步骤后,接下来在制图软件中对驱动桥壳进行建模,驱动桥壳模型最终三维图如图2所示。

图2 驱动桥壳三维图
桥壳所用的材料为40Cr调制合金钢,屈服强度σs≥785 MPa,密度ρ=7.9 g/cm3,泊松比0.3,弹性模量E=2.06E+11 Pa。
本文中所采用的有限元单元类型为10节点四面体单元,网格大小为5 mm,对桥壳进行划分后,网格单元的总数量为1 026 160个,节点数为1 595 527个。
2 驱动桥壳的模态分析
2.1 模态分析理论
分析系统的整体有限元方程为:
(1)
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;qt为节点位移向量;Ft为力向量。
1)无阻尼情形。
此时阻尼系数υ=0,则式(1)退化为:
(2)
2)无阻尼自由振动情形。
此时υ=0,Ft=0,则式(1)退化为:
(3)
式(3)有解的形式为:
(4)
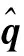
(5)
与式(4)联立消去eiωt后,得到以下公式:
(6)
该方程有非零解的条件是:
|K-ω2M|=0
(7)
2.2 桥壳自由模态分析
建立完驱动桥壳的三维模型和有限元模型后,接下来对驱动桥壳进行模态分析。通过对驱动桥壳的自由模态分析可以很直观地看到桥壳的整体和部分结构是否合理,在本文中,对驱动桥壳的自由模态分析是对桥壳不施加任何载荷和约束的情况下进行的[6]。在有限元软件中,通过对桥壳划分网格,设置分析求解步骤,得到了桥壳的前12阶固有频率和振型图,由于桥壳前6阶的自由模态为刚体模态,固有频率接近于零,所以只展示了桥壳7~12阶弹性模态的固有频率和振型,桥壳的自由模态如图3~图8所示。

图3 桥壳第7阶自由模态
表1为驱动桥壳在自由模态下的7~12阶固有频率和位移。由表可知:桥壳最大形变量发生在第9阶,最大变形为20.551 mm,该阶模态的主振型为绕Y轴弯曲,最大形变量发生在桥壳两边的半轴套管轴头处,产生这种变形的原因主要是,在汽车实际运行过程中,两边的轴头处承受了来自汽车轮胎与地面之间的反作用力和扭转转矩。由表1可知,驱动桥壳的7~12阶自由模态中最低固有频率已经超过100 Hz,远远大于汽车在0~50 Hz下和地面相互作用而产生的共振频率,由此可知,在自由模态下驱动桥壳的结构符合使用要求。

图4 桥壳第8阶自由模态

图5 桥壳第9阶自由模态

图6 桥壳第10阶自由模态

图7 桥壳第11阶自由模态

图8 桥壳第12阶自由模态
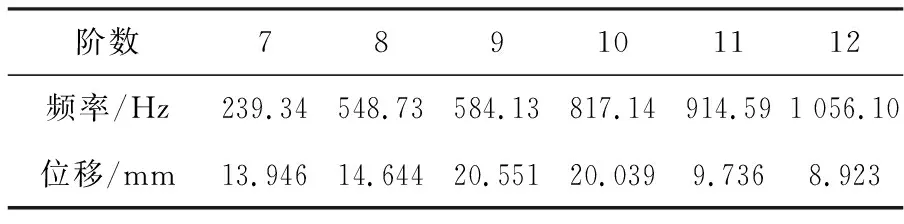
表1 自由模态下桥壳7~12阶固有频率与位移
3 桥壳自由模态试验
为验证在有限元仿真软件中对驱动桥壳分析的准确性与合理性,本节将对驱动桥壳进行在自由状态下的频响试验[7-8],具体操作步骤如下:
1)驱动桥壳的搭建。
在开始试验前,对试验器材进行准备与检查核验,驱动桥壳的试验架搭建及悬挂细节展示如图9所示。

图9 桥壳的试验架搭建
由于试验条件限制,采用两个高脚凳作为试验的台架,目的是保证桥壳处于悬空状态(从分析结果来看,台架的试验效果是较为合理的)。为保证试验的准确性,使已经搭建在台架上的桥壳处于悬空状态,同时在吊起来的桥壳上连上加速度传感器。
通过图10可以看到,在驱动桥壳两边的半轴套管处使用了适当的弹力绳,通过这种方式来模拟实现桥壳的自由状态,同时也通过这种方式来减小试验过程中产生的误差。

图10 桥壳的半轴套管悬挂展示
2)试验器材的准备。
搭建好桥壳的试验架后,开始准备试验所用的器材,并对测试用的试验器材进行调试,所用到的试验器材包括:1台试验测试主机,1个测力锤,1个游标卡尺,1支白色油漆笔,1个加速度传感器,4根通道连接线,弹力绳若干,1个试验架,1台服务器。测力锤、加速度传感器以及分析测试仪器如图11~图14所示。

图11 试验测力锤 图12 加速度传感器

图13 测试系统正面 图14 测试系统反面
3)桥壳的模态试验。
驱动桥壳试验前期工作准备好后,开始进行驱动桥壳的自由模态试验[9-10],具体的操作如下:
①因为在测试软件中只能显示结构的节点勾勒出的轮廓图,所以在服务器的测试软件中要画出驱动桥壳的测点图,本文对驱动桥壳的试验测点设置为110个,试验方法为单点实振(激励)。
②对桥壳进行数据采集。在数据采集界面,包括几个部分:力的采集、加速度的采集、响应的采集、信号的采集、信号的相干性采集等。虽然每个界面反映的参数不同,但是它们反映的都是同一次频响,同一次敲击的信号是相互关联的。
③在动态信号测试分析软件中对驱动桥壳的频率响应试验结果进行分析,得到驱动桥壳的试验频率响应图。
④通过振型值最大归一方法计算出驱动桥壳固有频率值,在测试软件中得到桥壳的前6阶固有频率,其对应的是桥壳在仿真分析中7~12阶自由模态的固有频率。通过试验得到的频率见表2。

表2 驱动桥壳自由模态试验频率
驱动桥壳试验完成后,接下来对仿真数据和试验数据进行对比分析。表3为驱动桥壳在有限元仿真分析软件中得到的数据和在试验中得到的数据的对比分析结果。
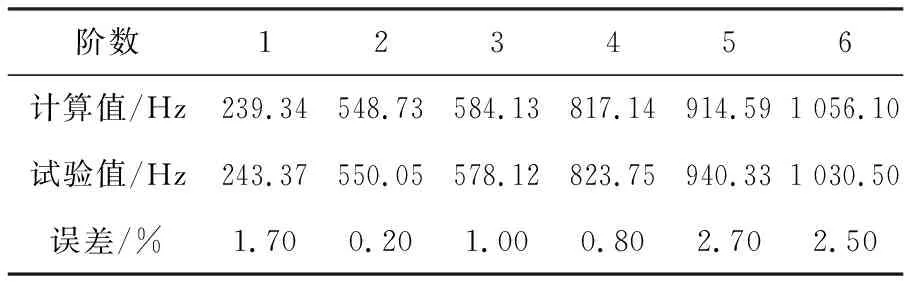
表3 桥壳固有频率仿真与试验对比分析
由表可知,两者的试验误差最大值仅为2.70%,最大数据误差在3%内,契合度相当高,两者的误差在一定范围以内,被认定是合理的。模态试验数据充分表明,在有限元软件中模拟仿真的数据是准确、合理的。
4 桥壳的随机振动分析
基于以上分析结果,对驱动桥壳的随机振动展开分析[11-13]。
首先在有限元分析软件中添加PSDGacceleration,其中PSD为功率谱密度,G是在模态分析中预设的模态阶数。边界条件选择沿着桥壳垂直的振动方向(在这里指的是Y方向),加速度谱设置为10(在设置中预设阶数为10),频率的范围值设置在最大阶数对应的频率的2/3以内,这里设置600 Hz,由于激励谱的分布为高斯分布,根据3σ原则(又叫拉依达准则),此时的置信参数设置为1σ,随机振动下1σ桥壳形变分析结果如图15所示。

图15 1σ下随机振动形变
在1σ参数设置中,桥壳的振动方向选择为Y方向(桥壳垂直振动方向),数据分析范围的等效应力下分布提取率为68.269%,这表示在随机振动分析时,系统中提取了68.269%的振动频率范围,包含了一半及以上的取值分析范围。
根据图15可得,在1σ下,桥壳的随机振动总形变为0.001 760 8 mm,为了验证仿真的合理性,对分析的数据进行计算:
(8)
式中:u为给定方向上的位移响应;γ为设定阶数下的参与因子,根据分析结果,取3.368 7E-04;φ为给定模态的振型,取0.617 7(一阶模态下最大振型);ε为阻尼,默认取0.02;M为给定模态阶数下的广义质量,对于一阶模态取M=1;f0为给定阶数模态的频率;PSD=10×9 800×9 800(10指的是预设阶数)。
计算得出u=0.001 225, 与仿真数据的误差为0.001 76-0.001 22=0.000 54 mm。可知仿真分析数据与计算数据之间的误差约为0.000 5 mm,说明仿真数据较为可靠、合理。
通过对驱动桥壳进行自由模态仿真分析与自由模态试验验证分析,并且基于此次分析结果,对驱动桥壳进行有限元随机振动仿真分析与公式计算结果对比分析,证明了驱动桥壳在自由模态分析下的随机振动的分析是合理的,分析数据表明驱动桥壳的结构设计较为可靠,刚度和强度满足使用条件。
5 结论
1)在自由模态仿真分析中桥壳最大的形变量发生在第9阶,最大变形为20.551 mm,该阶模态的主振型以绕Y轴弯曲为主,最大形变量发生在两边的半轴套管轴头处,产生这种变形的主要原因是汽车在实际运行过程中桥壳两边的半轴套管轴头处不仅承受了来自驱动车轮与地面之间的反作用力,而且还承受着汽车行驶时车轮在扭转弯曲方向上产生的扭转转矩。
2)通过驱动桥壳的有限元仿真数据与试验数据的对比分析可知,两者的数据误差最小仅为0.20%,误差最大仅为2.70%,可以看到驱动桥壳弹性模态所在的阶数误差都在3%以内,驱动桥壳的试验数据表明桥壳的仿真模拟计算与试验计算的结果高度符合,契合度很高,从而也验证了仿真数据的合理性与准确性。
3)在自由模态分析以及模态试验验证的基础上,通过对驱动桥壳的随机振动分析可以得到,当置信参数设置为1σ时,有限元仿真分析与计算误差约为0.000 5 mm,计算结果与仿真结果相近,误差很小,从而证明了在模态分析下随机振动仿真分析结果是合理的,同时也表明了驱动桥壳整体结构的强度和刚度满足使用条件。
