一类具有线性和非线性耦合项的Kirchhoff型方程组的基态解①
2022-04-20李振辉许丽萍
李振辉,许丽萍
河南科技大学 数学与统计学院, 洛阳 471023
本文研究如下一类Kirchhoff型方程组:
(1)
其中Ω是RN中的光滑区域,N≤3,V(x)是位势函数,ai,bi,λi,μi(i=1,2)是正数,k,β是耦合项系数. 为了研究方程组(1)解的存在性, 假定位势函数V(x)连续且满足如下条件:
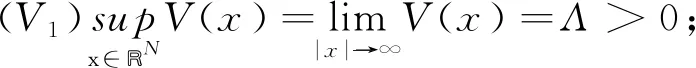
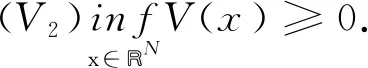
方程组(1)中u和v表示位移,bi是初始张力, 而ai与弹性弦的固有性质有关[1]. 如果V≡0, 那么方程组(1)变为
(2)
如果v≡0,k=0,β=0, 那么方程组(2)可以化简为如下Kirchhoff型方程:
(3)
方程(3)是文献[2]首次提出的, 用来描述弹性弦的自由振荡问题. 随后, 文献[3]用变分法研究了Kirchhoff型方程, 很多学者也对此产生兴趣, 获得了一些重要成果[4-7]. 对于不含非局部项的相关结果可参见文献[8-10].
(4)
文献[11]用Nehari流形证明了方程组(4)基态解的存在性.k=0时的一些成果见文献[12-16].
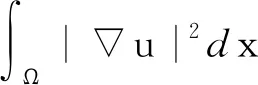

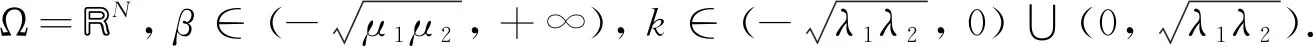
1 预备知识

(5)
和范数
(6)
2 定理1的证明

若Ω=RN, 设
H=H1(RN)×H1(RN)
定义H上的内积如(5)式, 范数如(6)式. 对∀(u,v)∈H, 设方程组(2)的能量泛函为
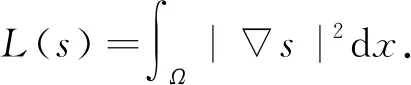
令
N={(u,v)∈H {(0, 0)}: J(u,v)=0}
易知, 方程组(2)的非平凡解(u,v)∈N. 下面先证明方程组(2)存在一个半平凡解, 从而可得N≠∅.
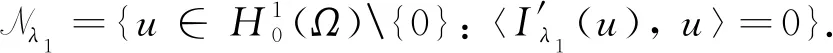
如果Ω=RN,a1=1,b1=0, 则方程(3)可以简化为
-Δu+λ1u=μ1u3u>0,u∈H1(RN)
(7)

注1若|Ω|<∞, 由引理1知方程组(2)存在一个半平凡解; 若Ω=RN, 由引理2知方程组(2)存在一个半平凡解. 无论哪种情形, 方程组(2)都存在一个半平凡解, 于是得到N≠∅.
引理3N是H的一个光滑子流形.
证对∀(u,v)∈N,
(8)
易见, 引理3成立.
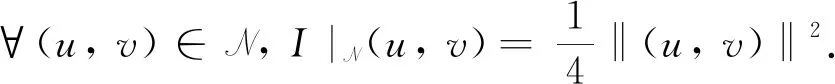
证若(u,v)∈N, 那么
J(u,v)=0
(9)
即
因此, 对∀(u,v)∈N,
由Sobolev嵌入定理得
既然‖(u,v)‖≠0, 那么存在C1>0, 使得对∀(u,v)∈N, ‖(u,v)‖≥C1>0.
引理5若(u,v)是I|N的临界点, 那么(u,v)也是I的临界点.
证若(u,v)是I|N的临界点, 那么I′(u,v)=ηJ′(u,v), 其中η∈R是一个Lagrange乘子. 于是
〈I′(u,v), (u,v)〉=η〈J′(u,v), (u,v)〉
由(8)式和(9)式得η=0. 引理5成立.
引理6若{(un,vn)}⊆H是I|N的PS序列, 那么{(un,vn)}是I的PS序列. 而且, 若Ω有界, 那么存在(u,v)∈N, 使得{(un,vn)}在H上有一个收敛于(u,v) 的子列.
I|′N(un,vn)=I′(un,vn)-ηnJ′(un,vn)
那么
o(1)=〈I′(un,vn), (un,vn)〉-ηn〈J′(un,vn), (un,vn)〉=-ηn〈J′(un,vn), (un,vn)〉
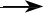
I′(un,vn)=ηnJ′(un,vn)+o(1)=o(1)
设

(10)
(11)
(12)
若Ω有界, 由Sobolev紧嵌入定理,c1和c2是存在的. 或者若Ω=RN, 由集中紧性原理可得c1和c2是存在的. 由引理4得
(13)
定理1的证明由c>0和文献[11]的引理2.2, 存在某个序列{(un,vn)}⊆N, 使得{(un,vn)}是I|N的(PS)c序列. 因此, 由引理6得{(un,vn)}是I的(PS)c序列. 根据对Ω的假定, 拟分两种情形讨论方程组(2)解的存在性.
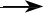
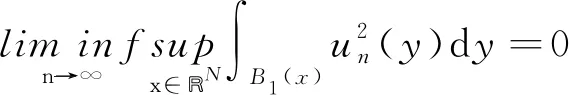

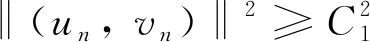
(14)
由引理4有

故有I(u,v)=c. 综上所述, 在两种情形下都有(u,v)∈N,I(u,v)=c,I′(u,v)=0. 因此,u≠0 和v≠0. 接下来, 讨论k取不同范围值时,u和v的符号.
首先, 设k<0. 则
由J(u,v)=0得
对t≥0, 定义一个C1函数φ(t)=I(t|u|,t|v|), 即
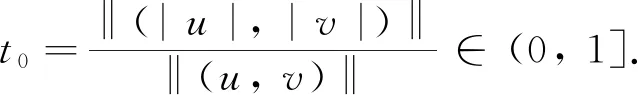
(15)
因此, ‖(|u|, |v|)‖2=‖(u,v)‖2, (|u|, |v|)∈N,I(|u|, |v|)=c. 不失一般性, 可假设u≥0,v≥0. 由引理5知, (u,v)是I的一个临界点. 因此(u,v)是方程组(2)的一个基态解.
由椭圆正则性定理知, ‖u‖L∞<+∞, ‖v‖L∞<+∞. 由于(u,v)是方程组(2)的解, 即
那么, 由最大值原理知
u>0v>0
(16)
再者, 设k>0. 由上述类似的讨论, 易知‖(|u|,-|v|)‖2=‖(u,v)‖2, (|u|,-|v|)∈N,I(|u|,-|v|)=c. 因此, 不妨设u≥0 和v≤0. 由引理6知, (u,v)是I的一个临界点. 因此, (u,v)是方程组(2)的一个基态解. 与(16)式的证明类似, 由椭圆正则原理和最大值原理得u>0,v<0.
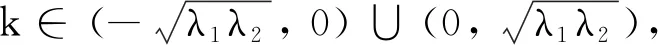
证由注1知, 存在u1>0和v1>0, 使得(u1, 0),(0,v1)∈N,c1=I(u1, 0),c2=I(0,v1). 因此
设g(t,s)=J(tu1,tsv1). 显然
g(1, 0)=J(u, 0)= 0
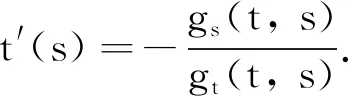
t′(s)=α(1+o(1))t(s)=1+αs(1+o(1))
t2(s)=1+2αs(1+o(1))
因此, 对∀s∈(-s0,s0), 有

3 定理2的证明
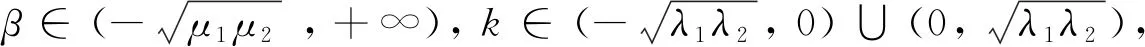

方程组(1)的极限情形是
(17)
设方程组(1)的能量泛函为
类似地, 定义方程组(17)的能量泛函为
设
定义Nehari流形
NV={(u,v)∈H1(RN)×H1(RN){(0, 0)}: JV(u,v)=0}≠∅
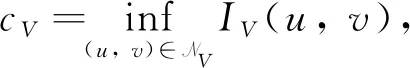
引理7假定V(x)满足条件(V1)-(V2), 那么cV Γ={γ∈C([0, 1],X):γ(0)=(0, 0),IV(γ(1))<0} 故有cV 接下来, 我们将用集中紧性原理和引理7证明定理2.


