地表反照率机器学习估算方法

吴锦超，吴永静，林超，窦宝成，刘锐

(1．广东省国土资源技术中心，广州 510000；2．北京吉威数源信息技术有限公司，北京 100043)

0 引言

地表反照率是广泛应用于地表能量平衡、中长期天气预报和全球变化研究中的重要参数之一[1-3]，其定义为：地表向半球空间反射的所有辐射能量与所有入射能量之比[4]。地表反照率作为能量平衡方程中的重要参量之一，反映了地球表面反射太阳辐射的能力，其时空变化受到自然过程(如降雪)以及人类活动(如森林破坏)等的影响，是全球环境变化的指示因子之一[5-10]。地球系统科学和气候变化研究对多种尺度、长时间序列、空间连续且高质量的地表反照率数据有着迫切的应用需求，因此，对卫星遥感估算地表反照率开展研究具有重要科学意义。随着对地观测技术的快速发展，传感器种类日趋丰富，卫星遥感方法为全球尺度、长时间序列地表反照率的估算提供了重要途径[11-14]。

目前根据不同卫星遥感数据特点结合多种数学物理模型发展起来的地表反照率反演方法众多，根据反演算法中使用模型的方式以及对遥感数据的利用方式，国际上主流的反照率生成算法主要包括基于反演二向性反射模型的反照率估算方法和直接估算反照率方法。为了支持全球长时间序列环境和气候变化的研究，2012年GLASS团队发布了第一版多种地表参数的长时间序列产品，2014年又更新到了第三版，其中的全球地表反照率产品具有时间序列长、时空连续一致的特点。GLASS全球反照率产品基于直接估算方法综合利用AVHRR、MODIS等遥感数据获取的目前全球最长时间序列的地表反照率产品[15-16]，已被应用在多个区域和全球尺度的研究中，包括：理解快速城镇化过程中的区域辐射强迫，中国东北地区的森林扰动，半干旱内陆河流域的蒸散发估算，辨识气候模式像元的空间变化及其影响[17]，验证、标定和改进气候模式中的模拟和参数化[18]，揭示全球森林的时空变冷和变暖效应[19]，估算日间净辐射[20]等。

业务化运行的遥感产品生成中往往采用半经验或经验线性模型来兼顾反演的精度和效率，GLASS反照率产品算法便采用多元线性回归的方法。近年来，机器学习方法在广泛的研究和工业领域备受青睐，很多优秀的机器学习方法和框架涌现出来。这些机器学习方法依赖现在强大的计算能力可以建立大数据集上或简单或复杂的各种回归模型，强大的模型为传统上复杂的遥感参数建模提供了一种新的可能。此外，对于传统上较简单的遥感参数建模，机器学习方法可以建立复杂度可控的模型来对反演精度调优。梯度提升决策树(gradient boost decision tree，GBDT)是集成学习中boosting算法中基于梯度下降迭代的回归树算法，适用于回归和分类问题。梯度提升决策树是使用大量的简单决策树对训练数据的不同特征建立模型，然后共同决策预测值。在回归中使用平方误差作为损失函数，每一棵决策树迭代上一轮所有决策树的预测结果并计算残差，通过迭代加性训练方法，在最小梯度上逐渐减小残差值，从而较快地获取较高的预测精度。梯度提升决策树方法目前在遥感上的应用还较少，Fan等[21]使用梯度提升决策树方法进行了空气污染的时空预测。近年来，基于梯度提升决策树方法的机器学习框架XGBoost[22]和LightGBM[23]以其快速高精度的特点在各大机器学习竞赛和工业应用中备受关注，它们也给大数据量遥感参数快速生成提供了一种新的思路。本研究以基于MODIS反射率数据估算反照率模型为例，采用梯度提升决策树算法，基于POLDER多角度观测数据集实现该模型。

1 数据

POLDER-3是可以在全球进行BRDF观测的星载传感器，其利用视场重叠获取多角度数据，单次过境时每个像元最多可有16个不同角度的观测，单个像元一个月累积的观测角度最多可达到300多个，基本可以实现全方位的角度观测。POLDER-3数据地表类型覆盖广泛，本研究采用基于POLDER-3 BRDF数据集构建的MODIS波段BRDF数据集进行反照率反演建模。POLDER-3 BRDF数据集经过筛选和插值生成各角度网格的地表方向反射率，然后进行波段转换得到对应于MODIS波段的植被、裸土和部分冰雪覆盖地表的训练数据集。模型模拟的冰雪BRDF数据集采用物理模型模拟不同参数下的纯冰雪像元BRDF数据。地表宽波段反照率数据是先对BRDF进行半球积分获得窄波段反照率，再通过窄波段反照率向宽波段反照率的转换公式得到地表宽波段反照率。角度格网模拟数据按太阳天顶角、观测天顶角和相对方位角生成：太阳天顶角范围是0～80°，每2°间隔进行划分，共分为41个间隔，格网中心分别为0°、2°、4°等。观测天顶角范围是0～64°，每2°间隔进行划分，共分为33个间隔，格网中心分别为0°、2°、4°等。相对方位角范围是0～180°，每5°间隔进行划分，共分为37个间隔，格网中心分别为0°、5°、10°等。因此，角度格网在太阳/观测角度空间共分成41×36×37=50 061个格网。

为了评估算法效果，利用地面站点观测的反照率同卫星反演反照率进行分析评价，地面参考反照率数据来自北美AmeriFlux、SURFRAD和ARM等观测网络的28个站点，站点信息如表1所示。

表1 反照率地面验证站点信息

2 方法

2.1 基于多元线性回归的反照率估算方法

GLASS反照率估算采用基于MODIS地表反射率数据直接估算反照率的算法(AB1)，可以利用MODIS传感器每天的地表方向反射率数据(已经过大气校正)直接反演地表宽波段反照率，生成日地表反照率中间产品。AB1算法的核心思路是建立MODIS地表方向反射率与地表宽波段反照率之间分格网的多元线性回归关系，首先采用POLDER-3/PARASOL BRDF数据集和模型模拟数据生成各种地表类型的MODIS地表方向反射率和地表宽波段反照率，然后进行分格网的回归。GLASS反照率估算是在反射率角度格网上进行多元线性回归，建立每个格网上MODIS地表方向反射率与地表宽波段反照率的回归关系，即转换系数，如式(1)、式(2)所示。

(1)

(2)

式中：αws是宽波段白空反照率；αbs(θs(k))是宽波段黑空反照率；θs(k)是太阳天顶角，取值0°～80°间隔5°，即k取值1，2，3，…，17；i取值对于MODIS数据而言为1，…，7，对于AVHRR数据而言为1，2，分别代表MODIS和AVHRR的短波窄波段；m0和n0(k)是回归表达式的常数项；mi和ni(k)是表达式的回归系数，回归系数按照角度格网和地表类型建立；ρi(θs，θv，φ)是方向反射率。

2.2 基于梯度提升决策树的反照率估算方法

不同于直接估算方法中采用的多元线性回归方法，本研究采用拟合能力更强的梯度下降决策树算法建立MODIS地表方向反射率与地表宽波段反照率的回归关系。在角度格网的反照率直接估算方法中，算法基于大量样本BRDF训练数据集建立角度网格上的线性回归关系。但实际上数据集可能存在非线性特性，此时使用非线性回归算法代替线性回归可以得到更加精确的结果，甚至可以建立角度连续的估算模型，从而缓解角度格网化离散降低精度的问题。这里以GLASS中基于MODIS的反照率估算为例，基于GLASS的多地表类型BRDF数据集采用机器学习方法建立MODIS地表方向反射率到宽波段反照率的估算模型。如果在所有角度上，对所有样本进行训练得到估算模型，相当于模型不依赖于角度格网查找表，可以直接估算任意角度的反照率。本文机器学习方法选择的是LightGBM框架的梯度提升决策树算法，模型的自我评价采用的是留余法，训练和测试数据集都是采用“标记数据+输入数据”的格式，标记数据为训练数据中的宽波段反照率，输入数据为窄波段反射率和角度等。

1)模型的构建策略。根据模型建立的粒度(即训练数据集的粒度)，模型的构建包括以下三种尺度。

(1)在单一角度格网上，对单一地表类型数据训练得到估算模型。这相当于还是依赖原有的格网查找表，但替换了原有的多元线性回归建立的估算模型。

(2)在部分或所有角度上，对单一地表类型数据进行训练得到估算模型。这相当于不依赖查找表，并且角度连续。

(3)在所有角度上，对所有地表类型数据进行训练得到估算模型。这相当于不依赖于查找表，角度连续且隐含类型，但此时训练数据集会异常庞大，一般机器难以运算。

2)训练和预测数据集的构建。GLASS BRDF数据集的反射率数据是角度格网化记录的，其中反照率数据首先存储白空反照率，然后存储黑空反照率数据，其中黑空反照率按照太阳天顶角递增的顺序排列，范围是0°～80°，间隔为4°，短波波段、可见光波段和近红外波段反照率依次存储。在进行学习训练时，每种反照率需要单独构建训练和预测数据集。

为了进行模型精度的自评价，采用了留余法。具体来说，首先将样本按等间距抽样划分为10组，具体操作为将1，11，21，…，n抽样为第1组，然后依次抽样剩下9组。训练和检验分10次进行，每次选择其中9组作为训练数据，剩余1组作为检验数据，10次精度评价结果的平均作为总体训练的精度。

3)模型的训练和预测应用。模型训练选择的是LightGBM工具和GBDT方法。为了能够客观评价模型的精度和泛化能力，模型训练和预测是在相互独立的训练和预测数据集上进行的。考虑到模型训练数据集大小的可操作性，模型的训练主要在两个层次上进行：一是分角度格网进行单独训练，二是按照角度格网的三个维度(太阳天顶角、观测天顶角和观测方位角)分别进行训练。模型的预测应用首先读取MODIS反射率数据集构建预测数据集，然后进行预测获取反照率。

3 结果与讨论

分别基于训练数据集采用MLR方法和GBDT方法建立模型，使用预测数据集的输入估算反照率，并以预测数据集的标记反照率为参考计算RMSE和R2，评价两种方法的精度。

3.1 分格网训练结果评价

以太阳主平面观测(RAA=0°)时的33个观测天顶角乘以41个太阳天顶角为例，分别使用多元线性回归(简称MLR)和GBDT方法，在每个格网尺度上建立模型并统计模型精度情况在角度格网上的分布，如图1所示。其中图1(a)和图1(b)分别是MLR和GBDT方法估算反照率的RMSE，图1(c)和图1(d)分别是MLR和GBDT方法估算反照率的R2，图中横轴是平面的太阳天顶角维，纵轴是平面的观测天顶角维。可以看出，太阳天顶角和观测天顶角均较大的格网相比于其他角度格网，两种方法估算的误差均较大、相关性较差，其中MLR方法估算的RMSE高达0.05，可决系数低于0.5，但GBDT方法在大角度时的精度衰减相比于其他角度不太显著。同时在太阳天顶角等于观测天顶角时的格网，也存在类似的精度衰减情况。在大部分的角度格网上，GBDT方法都比MLR方法具有更低的RMSE和更高的R2。

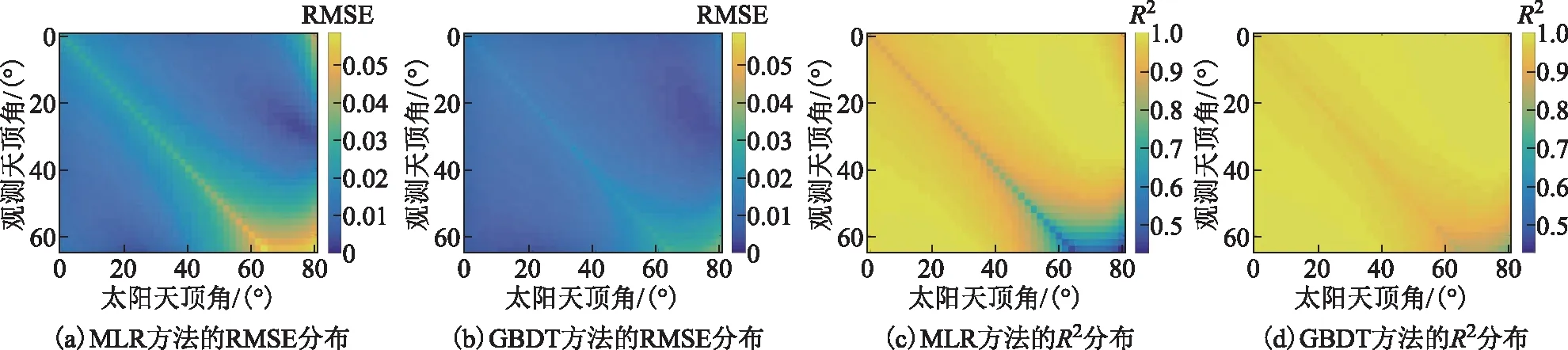
图1 太阳主平面下角度格网的精度分布比较

图2 太阳主平面下所有角度格网的RMSE和R2频率分布

进一步，对RMSE按照0.01间隔，对R2按照0.1间隔统计MLR方法和GBDT方法的RMSE和R2分布。图2给出了太阳主平面下所有角度格网的RMSE和R2的频率分布。在RMSE小于0.02的格网统计中，GBDT方法格网占比94.5%，而MLR方法格网仅占69.6%；在RMSE小于0.01的格网统计上，GBDT方法格网占比近半数47.8%，而MLR方法格网仅占24%，GBDT方法相比MLR方法有比较明显的精度提升。在R2大于0.9的格网统计中，GBDT方法格网占比97.2%，MLR方法格网占比84.9%，GBDT方法有更好的相关性。

3.2 单类不同粒度格网组合训练结果评价

不同于原来的MLR方法，GBDT方法可以在不同的数据集粒度上建立统一模型，因此在单一角度格网、单一平面单一观测天顶角、单一平面和多平面基础上分别建立GBDT模型并进行精度对比。图3给出了不同粒度下建立的GBDT模型与格网MLR方法精度比较的结果，图中估算反照率为两种方法估算的反照率，参考反照率为预测数据集给出的参考反照率。四种粒度数据集包括：(a)RAA=0，VZA=0，SZA=0，也即单一角度格网；(b)RAA=0，VZA=0，也即单一平面单一观测天顶角，太阳主平面天底观测；(c)RAA=0，也即单一平面，太阳主平面；(d)RAA=0～50，也即多平面。在较多数据集的统计结果上，MLR方法的RMSE为0.017到0.02，GBDT方法的RMSE为0.009到0.013；MLR方法的R2为0.934到0.956，GBDT方法的R2为0.972到0.987。可以看出，在四种粒度的数据集上建立的GBDT方法无论在RMSE还是R2上均优于MLR方法。

学习算法的精度依赖于模型对于数据集的表达能力。从图3可以看出，单一平面训练数据集GBDT的结果(图3(c2)，样本数量超过4 500万)和多平面训练数据集GBDT的结果(图3(d2)，样本数量超过5亿)相比单一平面单一观测天顶角数据集机器学习的结果(图3(b2))，模型的精度有所衰减，这主要是由于模型对于数据集的表达能力不足导致的，因此应该增加学习模型的复杂度。多决策树方法可以通过增加模型中树的数量进而增加模型的复杂度，对单一和多平面数据集时，分别设置5 000棵树代替原来设置的1 000棵树重新训练评价，两种设置的估算结果如图4所示。图4(a)和图4(b)分别是单一平面下1 000棵树和5 000棵树的估算结果，图4(c)和图4(d)分别是多平面下1 000棵树和5 000棵树的估算结果。可以看出，5 000棵树模型相比于1 000棵树模型，在单一平面数据集上将R2由0.972提升到0.979，将RMSE由0.013降到0.011；在多平面数据集上将R2由0.975提升到0.982，将RMSE由0.012降到0.01。可见，增加决策树数量可以在大数据量训练时提升估算模型的精度。

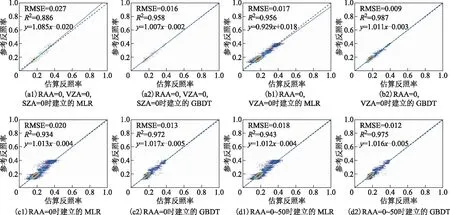
图3 MLR和GBDT方法在不同粒度数据集上的精度比较

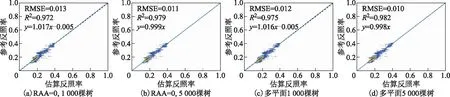
图4 不同树数量设置下的GBDT方法精度

3.3 基于地面站点观测的算法精度评价

为了评价提出算法的效果，本文一方面从地面站点测量数据提取短波反照率作为参考值，另一方面收集了GLASS V3版本反照率产品并提取各站点的短波反照率，同所提出算法生产的短波反照率进行比较。考虑到GLASS V3版本的生产时间到2013年，因此选择精度评价的时间范围是2011—2013年。图5给出了本文算法和GLASS V3反照率产品在北美28个站点的验证结果，图中GLASS新算法反照率代表本文算法反照率，GLASS V3算法反照率代表GLASS V3版本反照率。从图中可以看出，本文算法相比GLASS V3版反照率精度有所提升，两者RMSE分别为0.257和0.268，本文算法相对提升4%；两者偏差分别为-0.001 6和0.004 0，本文算法在绝对偏差上相对提升60%。

图5 不同算法反照率与地面实测反照率的验证结果

4 结束语

地球系统科学和气候变化研究对长时间序列、空间连续且高质量的地表反照率有着广泛的应用需求，目前的对地观测可以支持1980年至今的长时间序列全球卫星反照率和近年高时空分辨率高精度全球卫星反照率产品的生成。本文提出了基于GBDT算法的地表反照率估算方法，并在分格网和格网组合两个尺度分别构建GBDT模型进行反照率估算。分格网的GBDT模型算法相比MLR精度有显著提升，在RMSE小于0.02的格网统计中，GBDT方法格网占比94.5%，明显高于MLR方法格网占比(69.6%)。在网格组合下的GBDT模型算法相比MLR精度同样有显著提升，统计的MLR方法平均RMSE为0.017到0.02，GBDT方法平均RMSE为0.009到0.013。同时，研究发现，提升GBDT模型的复杂度(决策树树木的数量)能小幅提升算法精度。基于地面站点观测数据进一步的评价可知，相比于GLASS V3反照率产品，本文方法在RMSE和绝对偏差上相对提升4%和60%。研究表明，新型机器学习方法在优化遥感经验或半经验模型中具有重要潜力。