空间约束混合伽马模型的SAR影像分割算法
2022-04-20石雪
石雪
(桂林理工大学 测绘地理信息学院,广西 桂林 541004)
0 引言
合成孔径雷达(synthetic aperture radar,SAR)技术具有全天时、全天候对地观测,以及良好的穿透能力,在自然资源调查和生态环境监测等方面发挥了重要作用[1-3]。而SAR影像的广泛应用主要依赖于影像分析与解译等技术,因此对SAR影像分析和解译方法的研究具有重要的价值和意义。
影像分割是影像分析的关键步骤,高效且精确的分割结果影响着影像分析后续步骤的精度。但由于SAR影像自身包含大量相干斑噪声,这给其分割方法的设计带来了很大的挑战。SAR影像分割方法可分为监督和非监督两种,其中深度学习影像分割是目前监督分割方法中的研究热点[4-5]。该方法先构建神经网络各层结构而形成分割模型,然后利用先验样本训练分割模型,最后采用训练后的分割模型实现影像分割。该类方法的分割精度依赖于分割模型的学习情况,由于遥感影像的先验样本有限且质量不均一,这导致该类方法的参数估计不准确,降低了分割结果的质量。非监督分割方法不需要先验样本,依据地物的强度、空间和纹理等特征实现影像分割,但分割效率和精度有待提高。常用的SAR影像非监督分割方法包括基于阈值[6-7]、区域[8-9]、模糊聚类[10-11]、统计模型[12-14]等方法。Goodman[15]从统计学角度对斑特征统计特性进行了研究,构建了斑特征统计模型,这为统计模型分割方法在SAR影像上的应用提供了有力的理论依据。自此,基于统计模型的SAR影像分割方法得到广泛的关注和研究。该方法的基本思路是依据SAR影像内像素强度服从同一概率分布这一假设构建似然函数,即SAR影像统计模型,并通过参数求解实现影像分割。常用于建模SAR影像统计特性的分布包括瑞丽分布、Weibull分布、G0分布和伽马分布,其中瑞丽分布和Weibull分布常用于SAR影像幅度的统计建模[16];G0分布在SAR影像强度的统计建模中具有较好的性能,但其表达式比较复杂[17];伽马分布常用于建模多视SAR影像强度的统计特性,且具有较好的建模能力,由于其参数较少且易于求解,在SAR影像统计建模中应用比较广泛[18-19]。另外,为了降低斑点噪声对分割结果的影响,学者们以先验分布建模像素空间信息,并根据贝叶斯定理,结合统计模型和先验分布构建模型参数后验分布,即影像分割模型,通过求解最优模型参数以实现影像分割[20]。该方法易于以概率方式将影像空间信息融入分割模型,提高影像分割精度。
近些年,有限混合模型以其有效建模像素强度统计规律的特点,成功应用于遥感影像分割[21-22]。有限混合模型研究的热点问题包括以下三个方面。一是影像统计模型的构建。根据像素强度统计特点,采用不同的概率分布定义组份,以更准确建模影像统计模型。常用的混合模型包括混合高斯模型[23]、混合学生t模型[24]和混合伽马模型等。二是像素空间关系的统计建模。混合模型仅利用了像素强度信息,为了减弱影像噪声影响并提高分割质量,对像素空间关系统计建模的研究成为热点问题之一,通常将像素空间关系融入组份权重先验分布,但同时增加了分割模型结构的复杂性,给后续模型求解带来了巨大的挑战。三是模型参数求解。统计模型方法将影像分割问题转化为参数求解问题,因此准确求解参数对实现精确的影像分割具有重要的意义。但由于分割模型结构复杂给参数求解方法的设计带来了挑战,一方面是由于组份概率分布结构复杂,如形状参数以伽马函数存在概率分布中,另一方面是由于对空间信息统计建模增加了模型结构的复杂性。
针对上述热点问题,学者们对混合模型SAR影像分割方法进行了大量的研究。依据SAR影像像素强度统计分布规律,采用混合伽马模型构建影像统计模型。考虑到SAR影像内斑点噪声的影响,学者们提出对影像进行滤波处理,再采用混合伽马模型建模处理后的影像,进而通过参数估计实现影像分割[25]。但由于影像滤波减弱了区域边缘和细节信息,这导致后续的影像分割难以获得精确的区域边缘或地物细节。为了提高SAR影像分割精度且避免滤波处理的缺陷,学者们提出结合混合伽马模型和区域划分的SAR影像分割方法,如李琴洁等[26]提出在以水平集方法获得影像子区域划分的基础上,采用混合伽马模型建模影像统计模型,采用邻域加权期望最大化(exception maximum,EM)方法求解模型参数;Li等[27]提出在影像多边形子区域划分的基础上,采用混合伽马模型构建像素强度之间的相似性测度,通过最小化目标函数实现SAR影像分割。上述分割方法比较依赖于区域划分的结果,容易产生过分割现象,且区域划分会忽略影像内地物细节信息,更适用于大面积地物影像分割。另外,由于形状参数以伽马函数的形式存在于混合伽马模型中,通过最大似然估计难以求解形状参数,通常将SAR影像视数设定形状参数,但降低了混合伽马模型建模像素强度统计分布的灵活性和参数估计的准确性,进而降低影像分割结果的质量。有学者提出采用统计模拟方法求解模型参数,虽然可求解出形状参数,但该方法需要进行大量参数采样,降低了分割方法的效率[28]。除此以外,有学者采用牛顿迭代方法求解形状参数的数值解,但增加了参数求解过程的计算量和复杂性[29]。
为了降低斑点噪声影响、实现高效且准确的SAR影像分割,提出结合空间约束混合伽马模型和共轭梯度的SAR影像分割算法。该算法采用混合伽马模型建模像素强度统计分布,为了降低噪声对分割结果的影响,利用局部像素类属概率定义组份权重,以将像素空间关系引入混合模型,构建空间约束混合伽马模型,在避免噪声影响的同时,简化了模型参数求解。为了高效且准确地求解参数,构建条件期望函数,采用共轭梯度实现最大化条件期望函数,不仅可准确求解模型参数,且具有较高的分割效率。在实验部分,对模拟影像和Radarsat卫星SAR影像进行分割实验,并定量和定性地分析实验结果。实验结果表明,所提出的算法可获得高质量的SAR影像分割结果。
1 所提出算法
令X={Xn;n=1,2,…,N}和S={Sn;n=1,2,…,N}为两个随机场,Xn和Sn为随机场X和S内第n个随机变量,O={1,2,…,O}和K={1,2,…,K}分别为Xn和Sn的状态空间,对于∀n,有Xn∈O和Sn∈K。一幅遥感影像可表示为像素强度集合,即x={xn;n=1,2,…,N},视为随机场X的一个实现,其中n为像素索引,N为总像素数,xn为像素n的光谱值,在状态空间O中随机变量Xn可取值xn,有p(Xn=xn)=p(xn)。影像分割即给每个像素分配一个标号,令标号集为z={zn;n=1,2,…,N},视为随机场Z的一个实现,其中zn为像素n的类属标号,在状态空间K中随机变量Zn可取值zn,有p(Zn=zn)=p(zn),K为影像内区域数,求解出标号集z即实现了影像分割。
1.1 空间约束混合伽马模型
假设SAR影像目标区域k内像素强度服从伽马分布,表示如式(1)所示。
(1)
式中:θk={αk,βk}为分布参数集;αk和βk为形状参数和尺度参数;Γ(·)为伽马函数。
像素隶属于目标区域k的先验概率分布,即Zn=k的边缘分布,表示如式(2)所示。
p(Zn=k)=wnk
(2)
根据贝叶斯定理,结合式(1)和(2)可得到像素强度的边缘概率,如式(3)所示。
(3)
进而,式(3)重新表示为式(4)。
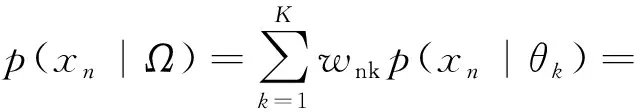
(4)
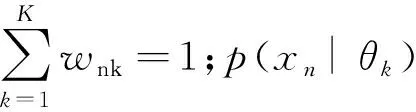
假设影像中像素之间相互独立,则像素强度的联合条件概率分布如式(5)所示。
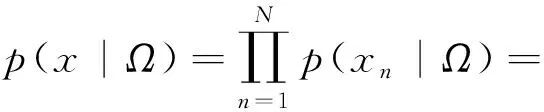
(5)
式中:Ω={w,α,β};w={wnk;n=1,2,…,N,k=1,2,…,K};α={αk;k=1,2,…,K};β={βk;k=1,2,…,K}。
为了克服SAR影像内斑点噪声的影响,并提高算法的分割精度,需将像素空间关系引入混合模型,同时不增加分割模型的复杂性,以便于降低参数求解的计算量。为此,所提出算法利用像素类属性定义组份权重。根据贝叶斯定理,可得到像素隶属于目标区域k的后验概率分布,如式(6)所示。
(6)
进而,令当前迭代中模型参数集为{w(t),θ(t)},其中t为迭代索引,将式(1)、式(2)和式(4)代入式(6)可得到像素类属后验概率,如式(7)所示。
(7)
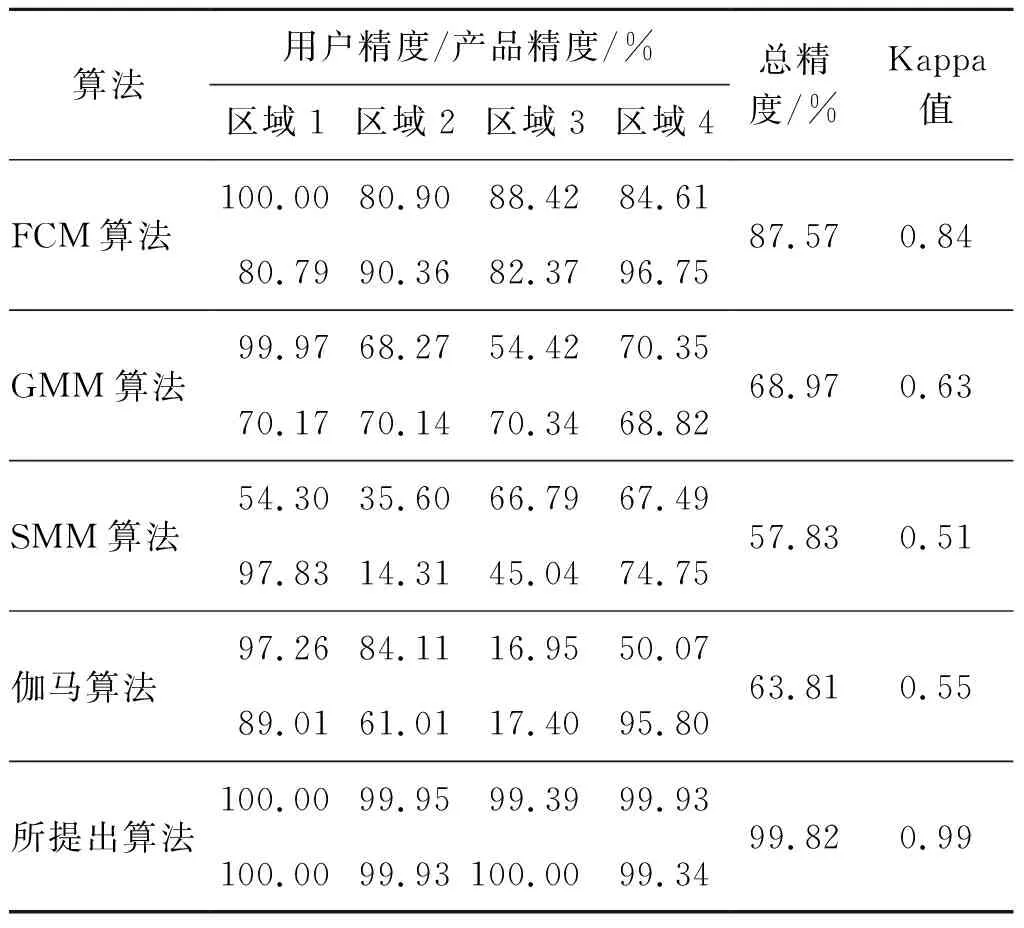
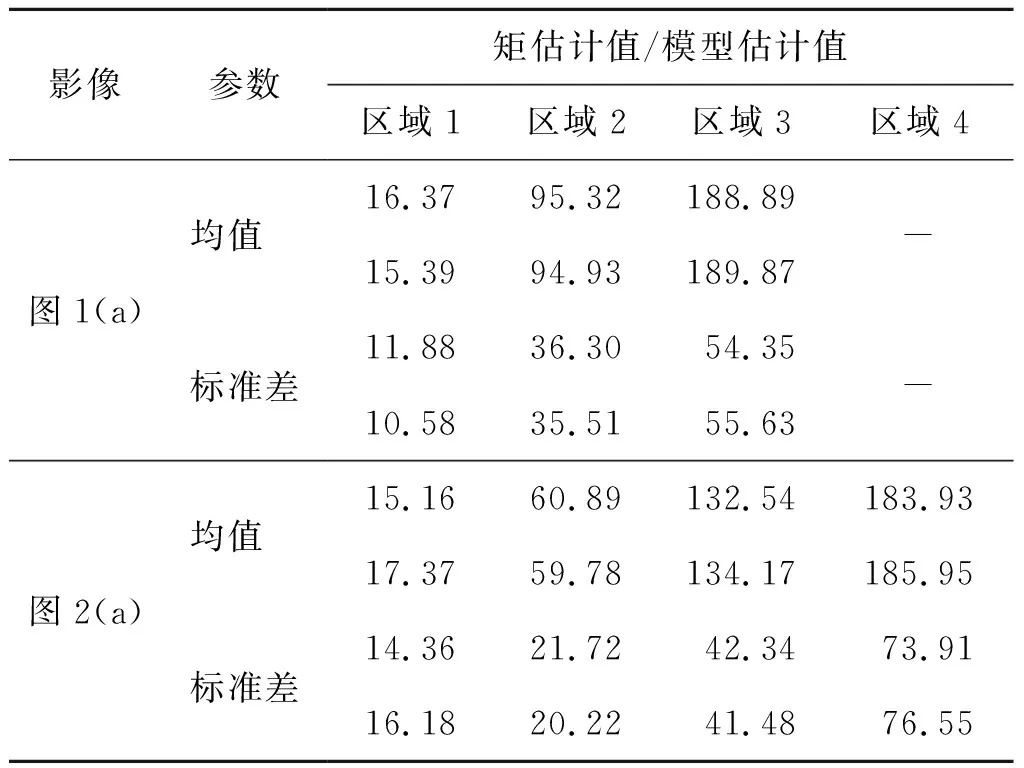
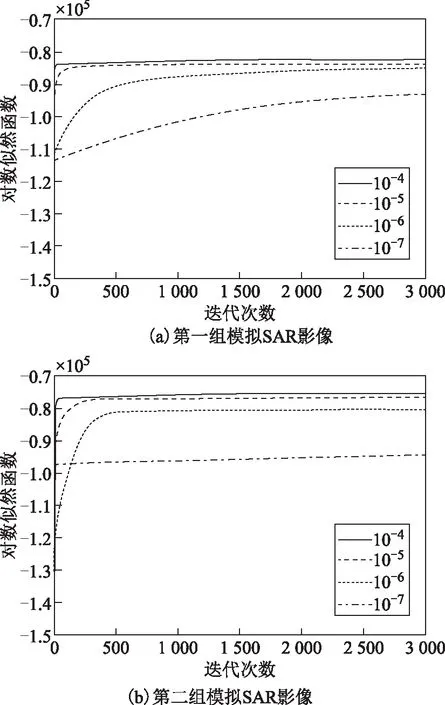
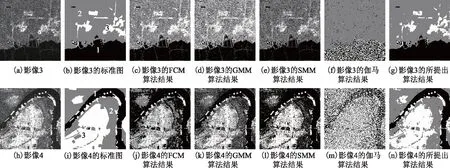
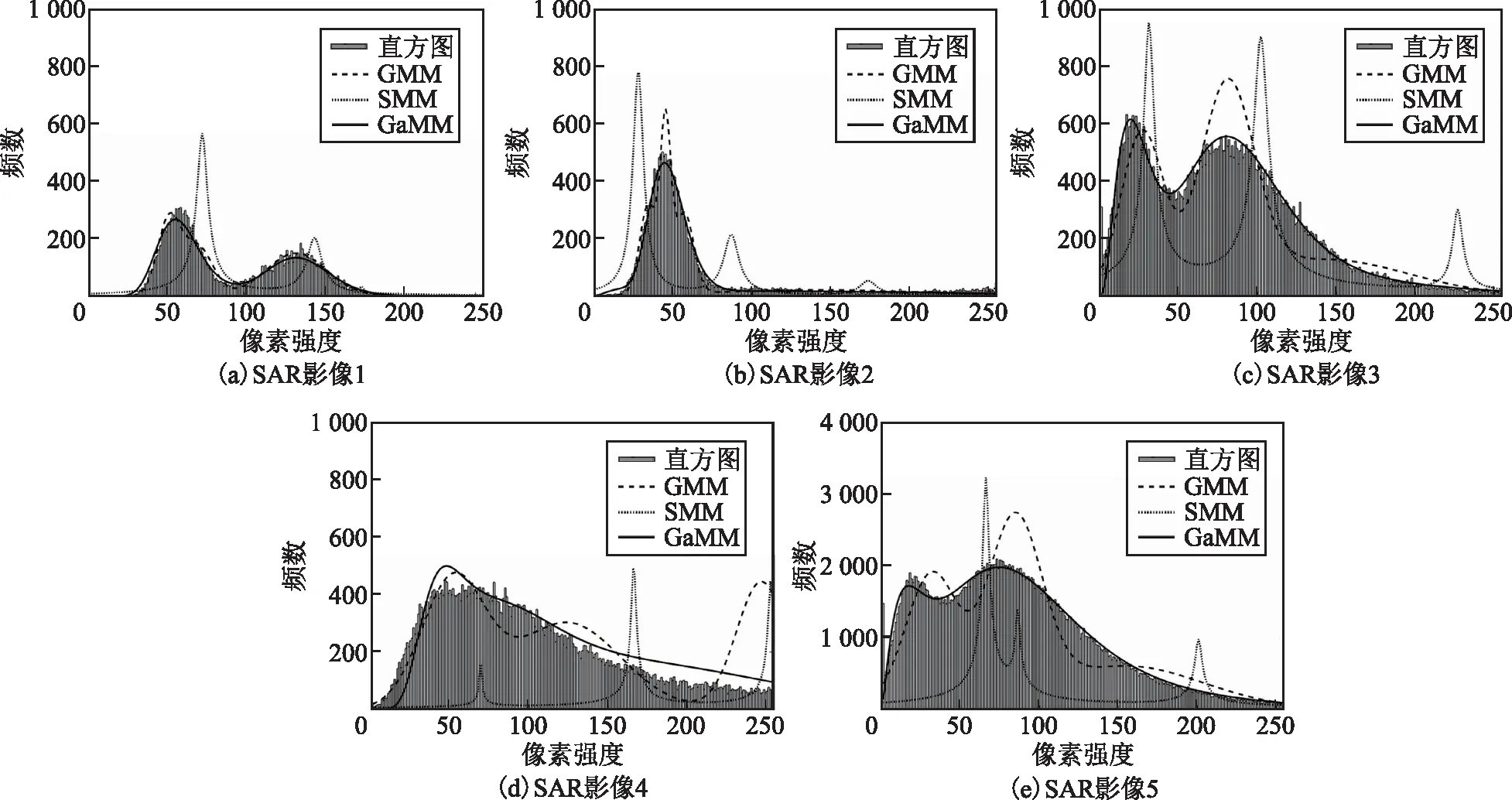
由于局部像素有更大可能性隶属于同一区域,因此将类属后验概率视为马尔可夫随机场,利用第t次迭代中局部像素的类属后验概率snk均值定义组份权重。为了满足组份权重0 (8) 式中:η为平滑系数,用于控制平滑程度,为了避免人为设置所产生的分割误差,将其设为随机变量,并在下一节对其进行求解;Rn为邻域像素索引集合,所提出算法取3×3邻域系统;n′为邻域像素索引;#为计算集合内元素数符号;t为迭代索引。将式(8)代入式(5)得到基于空间约束混合伽马模型的SAR影像统计模型,如式(9)所示。 (9) 令待求解参数集为Ψ={α,β,η},对式(9)取对数得到关于参数集Ψ的对数似然函数,表示如式(10)所示。 (10) (11) 式中:不等号右侧项为式(10)对数似然函数的下限函数,即其条件期望函数,当参数集Ψ为对数似然函数极值点时,不等式的等号成立。因此,通过最大化式(11)右侧项可达到最大化对数似然函数目的,避免了包含和对数项函数的参数求解困难问题。条件期望函数表示如式(12)所示。 (12) 由于形状参数以其伽马函数形式存在式(12)中,增加了参数求解的困难。为此,所提出算法采用共轭梯度求解模型参数,依据共轭性构建共轭方向以搜索使式(12)达到最大化的参数,该过程仅需计算参数的梯度,可避免分割模型结构复杂的问题。给定第t次迭代的参数集Ψ(t),可计算新的参数集(式(13))。 (13) 式中:λ为步长;DΨ={Dα,Dβ,Dη}为参数搜索方向集,为了避免梯度下降法产生锯齿现象导致参数收敛慢的问题,根据共轭性利用参数梯度可构建共轭搜索方向[30],其中初次搜索方向为梯度方向,即有DΨ(0)=GΨ(0),之后的搜索方向表示如式(14)所示。 (14) 式中:GΨ={Gα,Gβ,Gη}为参数梯度集。形状参数梯度表示为Gα={∂E(Ψ|Ψ(t))/∂αk;k=1,2,…,K},利用式(12)计算其关于形状参数αk的梯度(式(15))。 (15) 式中:ψ(αk)=Γ′(αk)/Γ(αk)。尺度参数梯度表示为Gβ={∂E(Ψ|Ψ(t))/∂βk;k=1,2,…,K},利用式(12)计算其关于尺度参数βk的梯度(式(16))。 (16) 将式(8)代入式(12),并用其计算平滑系数的梯度Gη(式(17))。 (17) 式(14)中φΨ为共轭系数,由参数梯度定义如式(18)所示。 (18) 总结提出算法的具体流程如下。 步骤3:利用式(15)~式(17)计算参数梯度; 步骤4:利用式(18)和式(14)计算共轭系数和方向; 步骤5:利用式(13)计算新的参数Ψ(t+1); 步骤7:利用式(10)计算似然函数,若似然函数收敛或参数收敛则停止迭代,否则,返回步骤2; 为了验证所提出算法的分割性能,在Intel Core i5-3470 CPU@ 3.20 GHz,8 GB内存系统环境下,使用MATLAB R2016a软件编程,采用所提出算法和对比算法实现模拟影像和Radarsat卫星的SAR影像分割实验,并定量和定性分析各算法的实验结果。其中,对比算法包括基于模糊C均值(fuzzy C-means,FCM)的隐马尔可夫随机场影像分割算法(简称FCM算法)、基于混合高斯模型的EM影像分割算法(简称GMM算法)、基于混合学生t模型的影像分割算法(简称SMM算法)、基于伽马分布的统计模拟影像分割算法(简称伽马算法)。 图1为第一组模拟SAR影像分割实验结果,其中图1(a)为包含三个目标区域的模拟SAR影像,图中各区域之间的边缘比较曲折,可有效检验提出算法对曲线边缘的分割能力;图1(b)为对应的标准分割结果图,1~3表示同质区域标号;图1(c)~图1(g)为采用FCM算法、GMM算法、SMM算法、伽马算法和所提出算法分割模拟影像得到的分割结果。比较各分割结果可以看出,对比算法的分割结果中存在大量的误分割像素,其中图1(c)中灰色区域内存在大量白色误分割像素,尽管FCM算法以隐马尔科夫随机场引用了局部像素类属标号相关性,但结果中仍然存在误分割像素;图1(d)中黑色和灰色区域内误分割像素比较多,图1(e)中仅灰色区域内存在较多黑色和白色的误分割像素,而GMM算法和SMM算法均采用MRF建模组份权重先验分布以考虑像素空间信息,但结果中仍存在大量误分割像素;与上述结果比较,图1(f)中灰色区域内误分割像素明显减少,伽马算法利用局部像素类属相关性构建标号先验分布,但结果中仍存在少量误分割像素;图1(g)中各区域内几乎不存在误分割像素,且所提出算法可准确拟合各区域之间的边缘。 图1 第一组模拟SAR影像分割实验结果 图2为第二组模拟SAR影像分割实验结果,其中图2(a)为包含四个目标区域的模拟SAR影像,图中各区域之间的边缘为直线,可有效检验提出算法对直线边缘的分割能力;图2(b)为对应的标准分割结果图,1~4表示各同质区域的标号;图2(c)~图2(g)为采用FCM算法、GMM算法、SMM算法、伽马算法和所提出算法分割模拟影像得到的分割结果。比较各算法的分割结果可知,FCM算法结果中各区域存在少量误分割像素,但区域3内部分区域被错误分割给白色区域,GMM算法和SMM算法结果中存在大量误分割像素,伽马算法难以将区域3和区域4分割开,而所提出算法可准确分割开各区域,结果中仅存在极少的误分割像素。 图2 第二组模拟SAR影像分割实验结果 为了定量分析所提出算法的分割结果,统计分割结果与标准图之间的混淆矩阵,并计算用户精度、产品精度、总精度和Kappa值,各精度值在[0,100%]之间,Kappa值在[0,1]之间,数值越大表示分割结果的精度越高。计算图1和图2内分割结果的精度,见表1和表2。从表1可看出,FCM算法各区域的精度在81%以上,GMM算法和SMM算法中区域2的精度较低,这是由于区域2内存在较多误分割像素,伽马算法各区域精度在90%以上,而所提出算法各区域精度在99%以上。通过比较各算法的总精度和Kappa值可知,GMM算法的最低,FCM算法和SMM算法均达到89%和0.84以上,而所提出算法的最高,达到了99%和0.99。从表2可看出,FCM算法各区域的精度在80%以上,而其他对比算法各区域的产品和用户精度均不高,由于大量误分割像素导致SMM算法区域2的用户精度约14%,伽马算法区域3的产品和用户精度在16%~18%,所提出算法各区域的精度在99%以上。通过比较各算法的总精度和Kappa值可知,SMM算法最低,GMM算法和伽马算法均不超过70%和0.63,所提出算法最高,达到了99%和0.99。综上,所提出算法可以获得高精度的分割结果。 表1 第一组模拟SAR影像分割精度 表2 第二组模拟SAR影像分割精度 依据图1(b)和图2(b)标准图,采用矩估计计算两幅模拟SAR影像各区域均值和标准差,作为标准参数,以验证所提出算法参数估计的准确性。利用所提出算法求解的形状和尺度参数估计值计算均值和标准差估计值,见表3。通过比较各区域参数估计值可看出,所提出算法的估计值与矩估计值最大差值不超过3,这间接体现出该算法可以准确求解组份参数。 表3 所提出算法参数估计 图3 不同步长条件下似然函数变化曲线 为了验证所提出算法中步长对分割结果的影响,绘制不同步长情况下似然函数随迭代变化曲线,如图3所示,图3(a)和图3(b)分别为图1(a)和图2(a)模拟SAR影像的似然函数曲线。从两幅曲线图可看出,似然函数曲线随着迭代次数增加而增加,并趋于稳定。当步长设为10-7时,似然函数值收敛后的数值较小;当步长设为10-6时,两幅模拟影像的似然函数值分别在1 500次和500次迭代左右收敛,收敛速度比较慢;当步长设为10-5时,似然函数收敛较快,且收敛后的函数值较大;当步长设为10-4时,似然函数值收敛最快,且收敛后的函数值最大,且与虚线相近,但容易产生过分割现象。因此,在实验过程中将步长设为10-5可得到最大似然函数值,进而获得最优分割。 图4为Radarsat-1卫星影像分割实验结果,其中图4(a)和图4(h)为两幅30 m分辨率128像素×128像素的SAR影像,图中包括不同融化程度的海冰,图4(b)和图4(i)为SAR影像的标准分割图。由于没有对应的标准分割图,因此通过目视解译绘制SAR影像的标准分割图,以便于定量评价各分割结果的精度。图中分别包含3或4个目标区域,1~4为不同区域的标号。采用对比算法和所提出算法对图4(a)和图4(h)SAR影像进行分割实验。从分割结果可以看出,各对比算法的结果中存在不同程度的误分割像素和错分区域。其中,FCM算法对图4(a)SAR影像的分割结果优于其他对比算法,但难以将图4(i)SAR影像的区域3和区域4分割开,如图4(j)所示;GMM算法难以将强度值相近的亮区域分割开,如图4(d)内区域2被错误地划分给区域3,以及图4(k)内区域3和区域4被划分在一起;SMM算法难以将强度值相近的暗区域分割开,如图4(e)和图4(l)内均将区域1和区域2划分在一起;虽然伽马算法的结果优于GMM算法和SMM算法,但仍然存在误分割像素,如图4(f)内存在灰色误分割像素和图4(m)内黑色误分割像素;所提出算法可以将SAR影像内各区域分割开,结果内仅存在极少误分割像素,且明显优于对比算法结果,如图4(g)和图4(n)。 图5为Radarsat-2卫星SAR影像分割实验结果。其中,图5(a)和图5(h)为两幅5 m分辨率256像素×256像素的SAR影像,图中包括建筑、水域、耕地等地物,图5(b)和图5(i)为对应的标准分割图,均包含三个目标区域,1~3为不同区域的标号。采用对比算法和所提出算法对图5(a)和图5(h)SAR影像进行分割实验,从分割结果可以看出,FCM算法、GMM算法和SMM算法中均存在大量误分割像素,尤其是图5(a)灰色区域内,伽马算法甚至难以将两幅影像各区域分割开,而所提出算法可以将各区域分割开,对于边界比较模糊的亮区域同样可分割开,仅在灰色区域内存在少量的误分割像素,其结果明显优于对比算法的分割结果。 图4 Radarsat-1卫星SAR影像分割实验结果 图5 Radarsat-2卫星SAR影像分割实验结果 为了定量评价上述SAR影像分割结果,计算各结果的分割精度即正确分割率,见表4。通过比较各算法的分割精度可知,FCM算法、GMM算法、SMM算法和伽马算法对四幅影像结果的分割精度不超过93%、69%、80%、74%,其中FCM算法分割影像1的精度比较高,而其他三幅影像的分割精度均不超过83%,GMM算法和SMM算法均在分割影像2的精度最低,分别约为43%和29%,伽马算法分割影像4的精度最低,约为46%,而所提出算法各结果的分割精度均在94%以上,明显高于对比算法的分割精度。综上,所提出算法可获得高精度的SAR影像分割结果。 表4 SAR影像分割精度 % 为了评价所提出算法的分割效率,记录其和对比算法的分割时间,见表5。影像1和影像2为128像素×128像素,影像3和影像4为256像素×256像素。通过比较可知,随着影像内像素数的增加,各算法的分割时间随之增加。通过比较平均分割时间可知,GMM算法的分割时间最少,具有最高的分割效率,这是由于该算法采用EM方法求解模型参数,可获得参数表达式,因此参数求解效率较高;FCM算法的分割效率虽然不如GMM算法,但其平均分割时间仍低于其他对比算法,具有较高的分割效率;SMM算法采用梯度下降法优化模型参数,该方法收敛慢,且需要通过多次迭代求解最优参数,导致该算法分割效率比较低;伽马算法采用统计模拟方法优化参数,需要经过大量迭代以达到算法收敛,导致该算法的分割效率最低;而所提出算法采用共轭梯度方法求解模型参数,可提高算法收敛时间,且适用于复杂模型求解,其平均分割时间仅比GMM算法多,优于其他对比算法。综上,各算法分割效率排序为GMM算法>所提出算法>FCM算法>SMM算法>伽马算法。 表5 SAR影像分割时间 s 图6 大尺度SAR影像及其分割结果 为了验证所提出算法分割大尺度SAR影像的性能,采用对比算法和所提出算法对大尺度SAR影像进行分割实验。图6(a)为512像素×512像素的Radarsat-2卫星SAR影像,包括水域、耕地和建筑三类地物,其中耕地(灰色)和建筑(白色)区域之间的边界比较模糊,易造成误分割现象。图6(b)~图6(f)分别为采用FCM算法、GMM算法、SMM算法、伽马算法和所提出算法获得的分割结果。从图6可知,FCM算法分割结果优于其他对比算法,但在白色和灰色区域之间边界处存在较多误分割像素,而灰色区域内存在黑色误分割像素;GMM算法难以将灰色和白色区域分割开,且各区域内均存在不同数量的误分割像素;SMM算法将大部分灰色区域像素错误分割为黑色,且各区域之间边界非常模糊;伽马算法难以将各区域准确分割开,且分割结果最差;所提出算法可有效降低斑点噪声影响,各区域内仅存在少量误分割像素,且灰色和白色区域之间边界清晰。另外,对于影像中水域内船舶,由于水域颜色较暗而船舶较亮,对比算法和提出算法将船舶与同样较亮的城市区域划分在一起。综上,所提出算法可获得大尺度SAR影像的高质量分割结果。 图7为上述五幅SAR影像的灰度直方图拟合结果,以验证所提出算法为最优模型。图中横纵坐标分别为像素强度值及其对应频数,柱状区域为SAR影像灰度直方图,利用GMM算法、SMM算法和所提出算法拟合各直方图,拟合曲线分别为虚线、点线和实线。从灰度直方图可看出,SAR影像直方图右侧尾部长且厚重,部分直方图的峰值不明显。其中,GMM算法对非重尾的直方图拟合较准确,如图7(a)虚线,但对于其他重尾特性直方图难以准确拟合;SMM算法中学生t组份具有尖峰和双侧重尾特性,其拟合结果不够准确;所提出算法中GaMM组份具有右侧重尾特性,可准确拟合重尾的直方图,如图7(c)和图7(e)实线,但对于尾部特别厚的直方图,所提出算法的拟合效果不够准确,如图7(d)所示。综上,所提出算法对SAR影像灰度直方图的拟合结果优于对比算法,为最优模型。 图7 SAR影像灰度直方图拟合结果 为了实现高效且准确的SAR影像分割,提出了一种结合空间约束混合伽马模型和共轭梯度的SAR影像分割算法。通过对SAR影像分割实验分析,得到以下结论。 1)所提出算法利用局部像素类属后验概率定义组份权重,构建空间约束混合伽马模型,避免了由于引入像素空间关系所产生的模型结构复杂、参数求解困难等问题,同时该模型可有效降低噪声的影响,获得高精度的SAR影像分割结果。 2)所提出算法采用共轭梯度实现最大化条件期望函数,可实现复杂结构的形状参数求解,获得最优参数估计值。由于该方法仅需计算参数梯度,因此适用于复杂模型结构的参数求解。另外,该方法可避免梯度下降法收敛慢的问题,具有较高的分割效率。 3)所提出算法将平滑系数视为随机变量,利用共轭梯度法实现自适应平滑系数的影像分割,避免了人为设置数值产生的过分割或欠分割问题。 综上,所提出算法对SAR影像分割具有良好的性能,但仍难以解决组份数确定的问题,这一直是混合模型分割算法研究中的热点问题,当前仍没有高效且普适的组份数确定方法,之后将针对这一问题进行研究。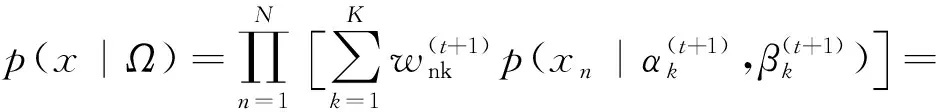
1.2 模型参数求解
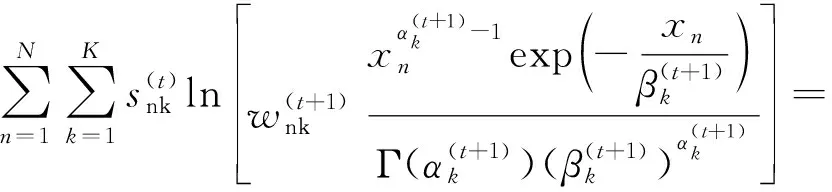
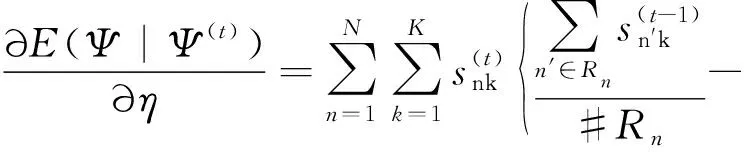
2 分割实验及讨论
2.1 模拟SAR影像分割



2.2 SAR影像分割




3 结束语
