混合mRMR和改进磷虾群的肿瘤基因特征选择算法

吴辰文，纪海斌

(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)

随着基因芯片技术的发展,研究人员能够快速、方便地获取大量基因微阵列数据,这些数据为疾病在分子水平上的诊断和分析提供了可能。基因微阵列数据属于典型的高维度数据,其中存在着大量与疾病诊断无关、噪声的基因,如何从中挖掘有价值的基因已成为对微阵列数据有效利用的关键所在[1-2]。分类是对微阵列数据最广泛的应用,然而微阵列数据具有维度高、样本少的特点,易引发维度灾难问题,对基因数据分类造成了巨大的阻碍。为解决这些问题,通常采取特征选择技术对数据进行约简,特征选择不仅能够筛选出对分类有利的基因子集,而且能够有效提高机器学习算法的性能和分类精度,但已知从大量特征中选择最优的相关特征子集是一个NP难题,为此,本文提出一种混合特征选择算法来有效选择相关的特征子集。

特征选择是指从已有的特征子集中选择更具有代表性的特征构成新的特征子集,所选特征子集相对原有子集更具代表性且具有更好的分类性能[3]。特征选择方法按照评价策略可以分为两类: 过滤式算法(filter)和封装式算法(wrapper)。过滤式算法不依赖于后续分类模型,通过观察数据集内在统计属性建立特征评分,根据排序准则函数选择得分较高的特征,该类算法简单、高效,但准确率不高。常见的过滤式算法有信息增[4]、ReliefF[5]、mRMR算法[6]、Fisher-Score[7]、基于相关的快速滤波算法(FCBF)[8]等。封装式算法则依赖于后续分类模型的分类准确度作为特征子集的评价指标,该类算法可以提供更好的准确性,但计算开销大。常见的封装式算法有SFS、SBS、PSO[9]、GA[10]等。

微阵列数据具有较高的维度,仅采用过滤式或封装式的特征选择算法难以获得最佳效果。对于高维数据的特征选择,有学者结合过滤式算法和封装式算法各自的优势,提出Filter-Wrapper混合特征选择方法[11],这类方法先利用Filter算法对特征集进行预选,过滤掉相关性小的特征,再利用Wrapper算法对预选特征集进行精选,能够更好地平衡分类精度和计算效率。

近年来,群体智能算法在解决特征选择问题方面被广泛应用,这类算法采用随机搜索的方式对特征进行组合优化,属于Wrapper算法。由于肿瘤基因数据是高维度数据,存在大量无关、冗余基因,单纯使用群体智能算法进行特征搜索难以达到理想的效果,基于过滤式算法和群体智能封装式算法的混合方法能够在分类精度和计算效率方面互补,在处理高维基因特征选择上具有较大的优势。例如,Akadi等使用混合mRMR和GA的两阶段算法对基因数据进行特征选择,并使用SVM和贝叶斯分类器进行验证,实验取得了良好的结果[12];Dashtban等使用Fisher评分产生高统计相关的基因特征子集,然后采用改进的多目标蝙蝠算法进一步寻优,使用4种分类器和留一交叉法进行验证,实验结果表明该方法的优越性[13]；叶超超等提出一种结合Relief-F和决策树的自适应粒子群优化算法(R-C-APSO),该算法不但具有较高的分类精度、较快的基因选择速度,而且具有良好的稳定性[14]。

磷虾群算法(KH)[15]是由Gandomi和Alavi提出的一种元启发式群体智能算法,该算法模拟了磷虾群体对特定危险和环境做出响应并逐渐提高种群密度的过程,相比其他群体智能算法,该算法具有更好的全局搜索能力,已被成功应用于参数估计、模型优化和分配调度等多种优化问题上。与其他群体智能算法一样,受到大量无关、冗余特征的影响,在高维数据上直接使用磷虾群算法进行特征选择存在计算效率低、效果差的问题。最小冗余最大相关算法(mRMR)[6]是一种非常有效的过滤式特征选择方法,但与其他过滤式算法不同的是,该算法能在筛选出与分类变量最相关特征的同时，使特征间的的差异最大化,但其获得的特征组合仍不能达到最佳效果。

肿瘤基因高维数据中存在大量不相关和冗余的特征,而与肿瘤类型识别相关的特征仅有很少的一部分,且难以通过穷尽所有特征组合的方式获取最优特征子集,因此,为了从肿瘤基因数据中获取与肿瘤分类相关的、且特征数量尽可能少的特征子集,本文利用mRMR算法具有能够过滤掉大量无关、冗余特征的特点,并结合磷虾群算法具有较强的全局搜索能力的优势,提出一种基于mRMR和磷虾群算法的肿瘤基因两阶段混合特征选择方法。此外,为了使磷虾群算法能够处理特征选择问题,使用编码转换原理对其进行离散化，并为了进一步提高磷虾群算法的全局搜索能力,采用了步长非线性递减和精英粒子局部搜索对其进行了改进。最后,通过多个肿瘤基因数据集对本文算法的效果进行验证,实验表明，本文算法在特征选择数量和分类精度方面具有优势。

1 相关算法

1.1 mRMR算法

最小冗余最大相关(mRMR)方法是一种过滤式的特征选择算法,其评价函数同时考虑了特征与类别、特征与特征之间的相关性,能够筛选出的特征子集同时具有最大相关性和最小冗余性。该算法采用互信息度量变量之间的相关性,两个变量的互信息表示为

(1)

其中：X和Y为两个特征变量；p(x)和p(y)为相应变量的边际概率函数；p(x,y)为联合概率分布。

给定候选特征子集,特征与类别间的最大相关、特征与特征间的最小冗余的度量分别为

(2)

(3)

其中,S为特征集合;fi为第i个特征；c为目标类别;I(fi,c)为特征i和目标类别c之间的互信息;I(fi,fj)为特征i与特征j之间的互信息。

考虑所选特征子集的相关性和冗余性,将式(2)与式(3)组合,得到mRMR特征选择算法的评价函数为

maxJ(D,R),J=D-R。

(4)

上述方程可通过逐渐增加单个变量来求解,假设集合S为全部特征集,St-1为已经选出的具有t-1个特征的特征集,则下一步任务就是从集合S-St-1中选择第t个特征，使上式最大化,也即通过式(5)最大化单变量相关性和冗余度的差值来确定添加的第t个特征。

(5)

1.2 磷虾群算法

磷虾群算法是一种仿生群体智能的优化算法,主要模仿了南极磷虾群在生存环境中不断提高群体密度,且逐渐聚集在高密度的食物区域的行为。磷虾个体会随着时间运动，且运动方向受周围磷虾的诱导、觅食活动、随机扩散3个因素共同影响,其位置更新方式为

xi(t+Δt)=xi(t)+Δt(Ni+Fi+Di)，

(6)

(7)

其中：Ni、Fi、Di分别代表磷虾个体的诱导运动、觅食运动、随机扩散运动;Ct为步长缩放因子;d表示总的变量数;Uj、Lj表示第j个变量的上界和下界。

诱导运动是磷虾个体受到最优个体和邻近个体的影响而产生的运动,表示为

Ni=Nmaxαi+wnNi,old。

(8)

其中：Nmax表示最大诱导速度;wn表示诱导权重;αi表示诱导方向。

觅食运动是磷虾个体朝着食物位置和自身的历史最优位置的方向移动,表示为

Fi=Fmaxβi+wfFi,old。

(9)

其中：Fmax为最大觅食速度;wf为觅食权重;βi为觅食方向。

随机扩散运动会增加磷虾个体运动的不确定性,表示为

(10)

其中：Dmax表示最大随机扩散速度；δ表示随机扩散方向。

此外,受差分进化算法启发,为了进一步提高算法的搜索能力,原算法中引入了交叉、变异遗传算子,分别表示如下:

(11)

(12)

其中：xgbest为全局最优个体；xp、xq、xr为随机挑选个体；m为维度；Cr为交叉概率，Cr=0.2Fiti,gbest，Fiti,gbest为个体xi与xgbest适应度差值的绝对值；Mu为变异概率，Mu=0.05Fiti,gbest；rand为[0,1]上均匀分布的随机数;0≤μ≤1。

2 基于mRMR和IKH的特征选择方法

对于肿瘤基因高维数据,使用基于过滤式和封装式的混合算法,能够充分利用过滤式和封装式算法各自的优势,选择出更有效的特征子集。为此,本文提出了结合mRMR和磷虾群的混合特征选择算法,用于处理肿瘤基因数据的高维特征选择问题。同时,针对原始磷虾群算法不能直接用于处理离散特征选择的问题,本文使用编码转换原理对其进行离散化处理;针对磷虾群算法存在不能平衡前期勘探和后期开发能力、局部搜索能力较弱的问题,本文引入步长调整、精英粒子局部搜索对其进行改进。此外,使用磷虾群算法特征选择时,需要合理设置适应度函数,适应度函数通常要综合考虑分类精度和特征数量。

2.1 磷虾群算法的离散化方法

为了使磷虾群算法能够处理特征选择问题,需要将磷虾个体的连续位置转化为二进制位置,每个二进制位置被用于表示特征是否被选择。本文使用编码转换策略[16-17],即每个磷虾个体有其对应的连续位置和二进制位置,磷虾个体在连续空间中运动,每个连续位置通过编码转换得到对应的离散二进制表示。磷虾个体的二进制转换表示为

(13)

其中:xij表示磷虾个体xi第j维的实值位置,xij取值为[-1,1];yij为对应磷虾个体yi第j维的二进制位置,yij∈{0,1}。

2.2 步长非线性递减

在磷虾群算法中，步长Δt可通过步长缩放因子Ct调节,而Ct在原文中被认为是应该根据具体问题仔细设置的参数,较小的Ct有利于进行精细搜索,较大的Ct有利于进行更大范围探索,而群体智能算法通常在前期应该进行更广泛的勘探,后期进行更局部的开发。但在原算法中，Ct被设置为常数,在优化过程中不利于勘探和开发。为了使整个迭代过程中前期勘探和后期开发平衡,本文采用指数非线性递减[18]对缩放因子进行调节,能够使整个优化过程前期具有较大步长,有利于勘探,后期具有较小步长,有利于局部开发,表示为

Ct＿min。

(14)

其中：Ct＿max和Ct＿min分别为Ct的最大值和最小值；tmax为最大迭代次数；t为当前迭代次数；τ为调节参数。

2.3 精英Fuch混沌变异优化

在磷虾群算法中,精英群体具有较高的适应度,能够有较大的概率接近全局最优解,对精英空间的有效探索能够进一步提高算法的搜索能力。混沌搜索具有遍历性、随机性,利用混沌对个体变异,能够提高粒子的多样性。为了进一步提高磷虾群算法的全局搜索能力,本文采用精英混沌变异对精英空间进行局部搜索,通过对精英空间的局部搜索提高算法的全局搜索能力。

在混沌映射中,Fuch混沌映射[19]相比Logistic和Tent混沌映射具有更大的混沌性,任何微小的初始差异都会造成结果很大的不同。因此,本文采用Fuch混沌映射在精英空间生成一个与本体完全不同的变异个体,Fuch混沌映射公式为

(15)

其中：k为迭代次数；zk取值为[-1,1]。

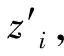
(16)

(17)

2.4 适应度函数

在进行特征子集评价时应该充分考虑分类精度和特征数量,即所选特征数量要尽可能少,得到的分类准确度要尽可能大[20],本文采用的适应度函数为

fitness=α·Acc+β·(1-S/T)。

(18)

其中：Acc为使用分类器分类得到的准确率；S为所选基因子集长度；T为总的基因子集长度；α和β分别为分类精度和特征子集长度重要程度,α+β=1。

2.5 mRMR-IKH算法过程

本文提出了mRMR-IKH混合特征选择方法,该方法结合mRMR和改进的磷虾群算法各自的优势,可用于高效处理高维数据特征选择的问题。算法流程图如图1所示,具体过程如下。

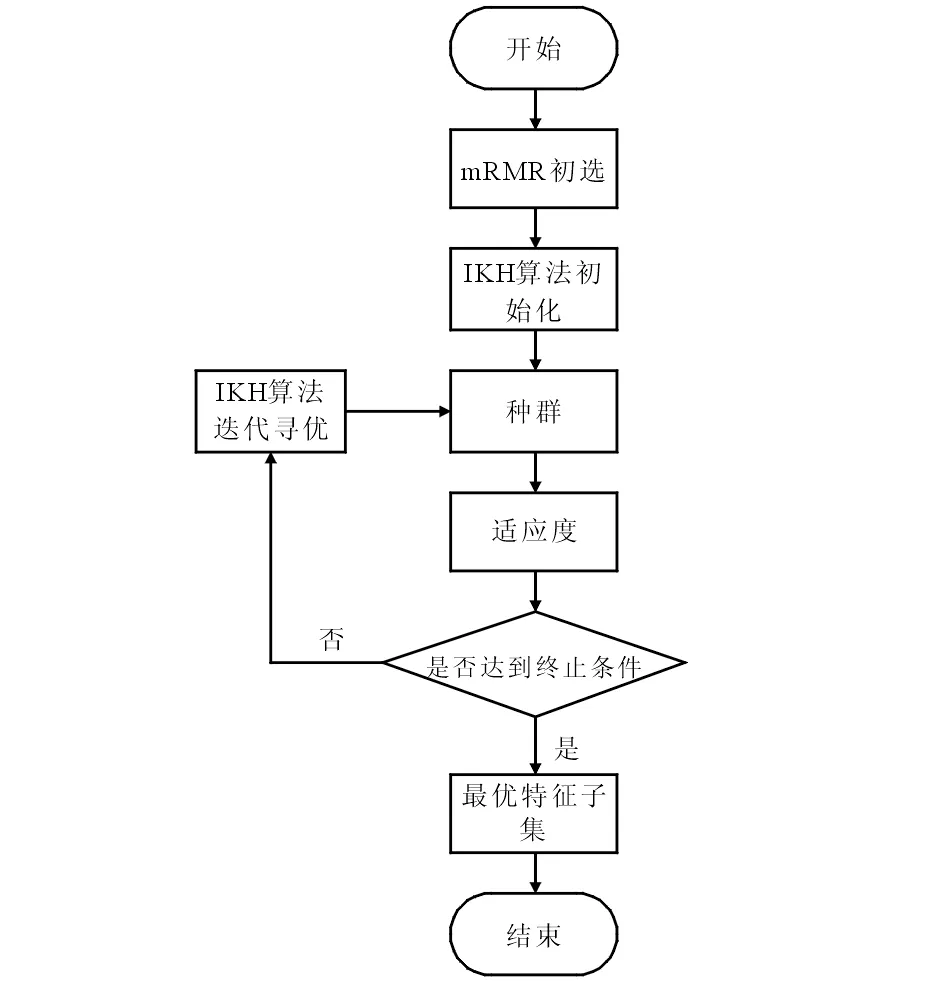
图1 mRMR-IKH算法流程图Fig.1 Flow chart of mRMR-IKH algorithm

Step1使用mRMR算法对各个特征进行评价,选择前S个特征为初选特征子集，并作为改进磷虾群算法的输入。

Step2种群初始化及参数设置,初始化磷虾实数位置xi(i=1,2，…,n),设置当前迭代次数t=1、最大迭代次数tmax、最大诱导速度Nmax、最大觅食速度Vf、最大随机扩散速度Dmax、诱导惯性权重wn、觅食惯性权重wf、最大步长缩放因子Ct＿max、最小缩放因子Ct＿min、指数调节系数τ、混沌变异概率R、精英个数m和混沌迭代次数k等。

Step3使用式(13)获取每个磷虾的离散化位置,根据式(16)计算磷虾个体的适应度。

Step4根据式(8)～(10)分别计算磷虾个体的诱导速度、觅食速度、随机扩散速度。

Step5根据式(14)计算步长缩放因子,并更新每个磷虾的运动速度和位置。

Step6根据式(11)和式(12)对每个磷虾进行遗传操作以增加种群的多样性。

Step7计算迭代后磷虾种群的适应度值,选取前m个最优个体组成精英空间，根据式(15)对精英个体进行混沌变异,计算混沌个体的适应度,将其与原个体对比,保留更优的个体。

Step8令t=t+1,判断是否达到最大迭代次数,是则结束,否则返回Step 4。

3 实验结果与分析

3.1 实验数据集

为了验证mRMR-IKH混合特征选择算法的有效性,本文选取6个公开的基因数据集进行实验,分别是ColonTumor、Lung、Leukemia、Prostata、MLL、SRBCT,其中,数据均经过最小最大归一化处理,各基因数据集的详情如表1 所示。

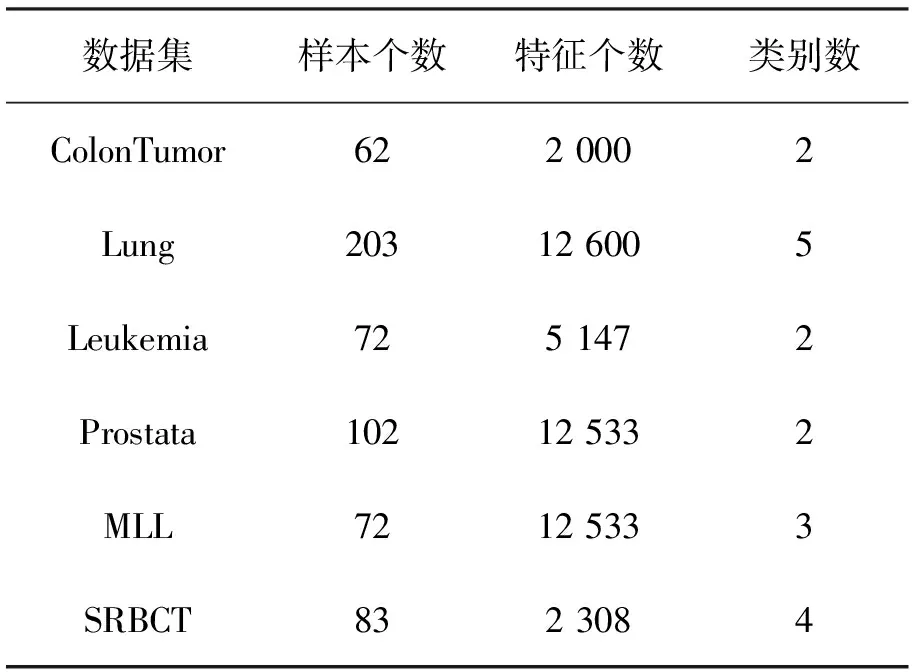
表1 肿瘤基因数据集Tab.1 Tumor gene data set

本次实验环境为64 位Windows 7操作系统,计算机处理器为i5-4590，3.3 GHz,内存8 GB,代码运行环境为Matlab 2016。实验采用SVM作为分类器,以SVM五折交叉验证的准确率和特征子集数量的加权和作为适应度函数,每一个基因数据集均独立进行10次实验,以10次实验结果的平均值作为最终结果。

3.2 实验结果与分析

为了验证mRMR-IKH算法的效果,将本文算法与其他算法进行对比实验,包括mRMR、mRMR+KH、mRMR+BPSO、mRMR+BBA。其中,由mRMR算法选择前100个特征作为初始特征,粒子数设置为50,迭代次数为300。

1)平均分类准确率和平均特征子集数量比较

为了比较本文算法的效果,采用10次独立实验平均后的分类准确率Acc和特征数量Fea作为比较对象,表2 给出了6个数据集使用5种算法运行得到的实验结果,同时给出了Acc和Fea的对应的标准差Std。

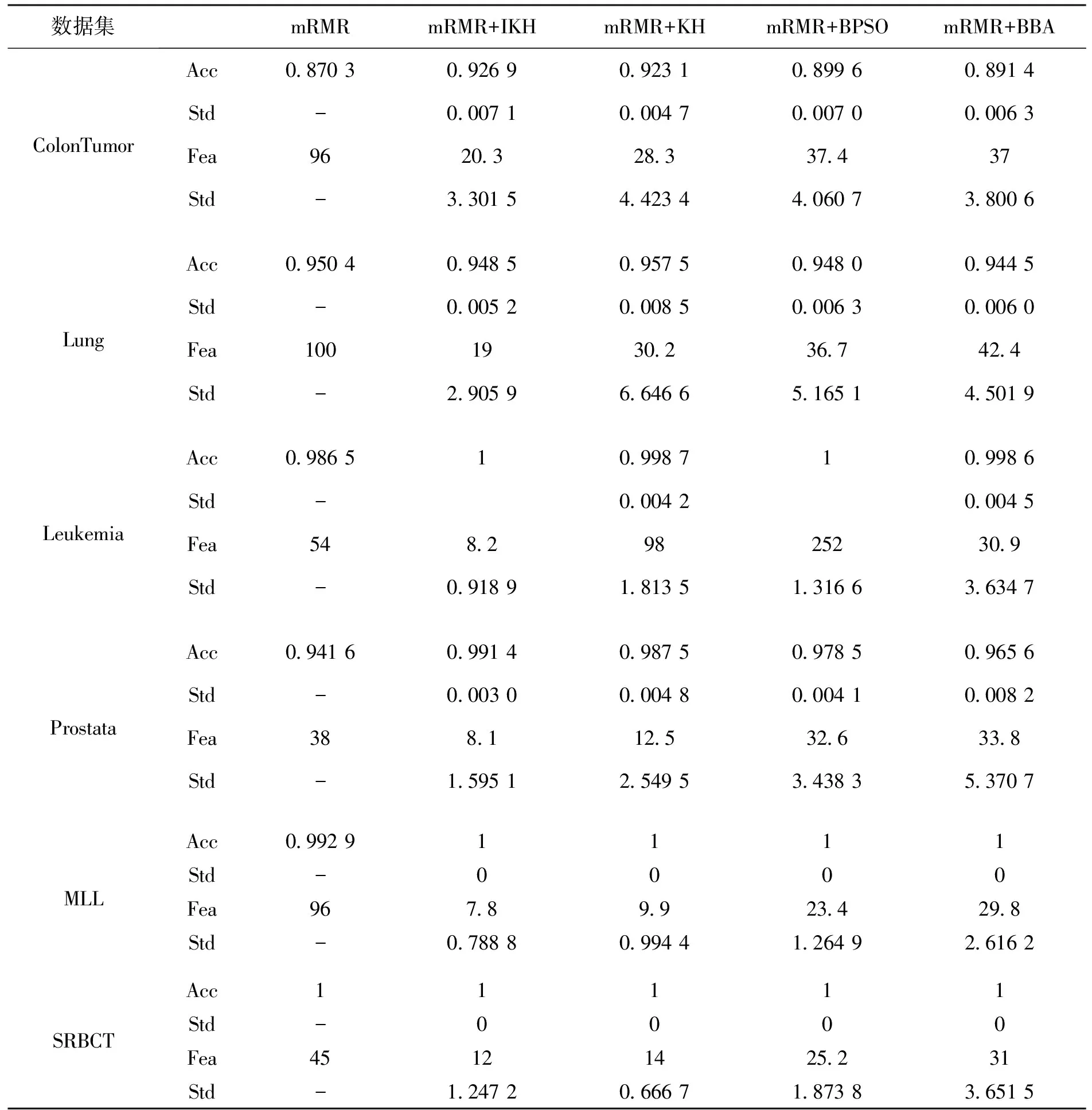
表2 5种算法在6个数据集上的平均准确率和平均特征数量比较Tab.2 Comparison of average accuracy and average number of features of 5 algorithms on 6 data sets

从表2可知,与单独使用mRMR算法相比,混合群体智能的算法普遍能够得到较少的平均特征数量和较高的平均准确率,这说明使用mRMR算法特征约减能力是有限的,使用群体智能算法能够对mRMR算法产生的特征子集进行进一步寻优,达到更好的效果。此外,与其他群体智能算法相比,在平均分类准确率方面,除Lung数据集外,本文算法均得到了最高平均分类准确率,而Lung数据集未能取得较高的分类准确率是由于Lung数据集是一个不平衡数据集,且在寻优过程中对特征的过度约减容易造成分类准确率的降低。在特征选择数量方面,本文算法均获得了最少的平均特征数量,这是由于本文算法采用的精英粒子混沌搜索进一步对精英空间进行了开发;从分类准确率和特征数量的标准差方面来看,本文算法相对其他算法具有良好的稳定性。

2)平均适应度曲线比较

为了进一步证明本文方法的有效性,将IKH算法在平均适应度曲线与KH、BPSO、BBA算法进行比较,在实验中分类准确率应具有较高的重要性,因此,在本文中α取0.9,β取0.1,实验结果如图2所示,其中横坐标为迭代次数,纵坐标为适应度。

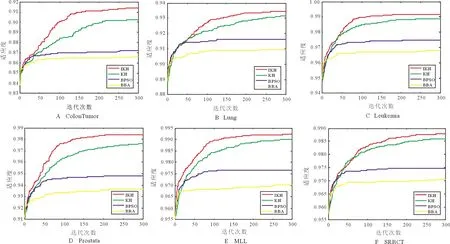
图2 4种算法在6个数据集上的平均适应度曲线比较Fig.2 Comparison of average fitness curves of 4 algorithms on 6 data sets

从图2中可以看出,本文算法在各个数据集上均能够得到最高的适应度,与BPSO和BBA传统算法相比,IKH算法能够对空间进一步开发,具有较强的全局搜索能力;与原KH算法相比,IKH算法引入了步长非线性递减和精英混沌搜索,通过对步长的调整平衡了前期的全局勘探和后期精细搜索的能力,通过精英混沌搜索增加了粒子多样性。从适应度曲线可以看出,IKH算法在迭代过程中能够进一步加强搜索,且具有较快的收敛速度。

综上分析,本文提出的mRMR-IKH算法结合了mRMR算法和IKH算法的各自优势,在mRMR算法提取特征子集的基础上进一步对特征约减,获得更加约减的特征子集,且具有良好的分类能力,同时IKH算法与其他3种智能算法相比,IKH算法具有更好的搜索能力,且稳定性较好。

4 结语

本文针对肿瘤基因高维数据集的特征选择问题,提出了一种基于mRMR和改进磷虾群(IKH)算法的混合特征选择方法。该方法通过mRMR算法筛选出一定数量相关但不冗余的基因,达到初步降维的目的,然后，利用磷虾群算法的寻优能力提取分类能力更强、更加精简的特征子集。本文使用编码转换原理将磷虾群算法二进制化,并采用步长递减和精英混沌变异进一步提高了其搜索能力。通过在6个基因数据集的实验结果表明,本文方法在选择的特征数量和分类准确度方面具有优势,是一种有效的肿瘤基因特征选择方法。本文算法采用精英局部搜索优化策略,时间复杂度有所增加,此外,参数需要人工调整,因此，下一步工作是研究如何通过设置粒子适应度停滞次数决定是否局部搜索以降低时间复杂度，并通过大量实验确定最佳参数设置以对算法进一步优化。