二维广义Camassa-Holm-Kadomtsev-Petviashvili(CH-KP)方程的局部适定性

王佳敏,可雪丽,臧爱彬

(1.西北大学 数学学院,陕西 西安 710127;2.湘潭大学 数学与计算科学学院, 湖南 湘潭 411105; 3.宜春学院 数学与计算机科学学院/应用数学研究中心,江西 宜春 336000)

在浅水波领域, 经典的模型包括Korteweg-de Vries(KdV) 方程[1]、 Camassa-Holm 方程[2-3]、Kadomtsev-Petviashvili方程[4]等。其中，Camassa-Holm方程[3]有如下表达形式:

ut-utxx+2κux+3uux=

2uxuxx+uuxxx,t>0,x∈

(1)

该方程是一个非线性色散波方程。 当κ>0时, 此方程可以模拟单向浅水波在平坦底部的传播, 并且u(t,x)表示t时刻在水平方向x上的流体速度[3，5]。关于KP方程的详细理论，可参考文献[4]和[6]。

CH方程的广义形式还可以模拟非线性波在直径较小的圆柱形超弹性杆内的传播[7]。在文献[8]中, Coclite等学者研究了广义超弹性杆波动方程(或广义Camassa-Holm方程)

t>0,x∈

(2)

其中，函数g:→给定,常数γ∈是根据材料常数和杆的预应力给定。若g(u)=2κu+3u2且γ=1,则方程(2)是经典的Camassa-Holm方程。若初值在H1()空间, 文献 [8] 证明了方程(2)整体弱解的强连续半群的存在性, 并且得到了弱解等于强解的唯一性结果。文献 [9] 在Xs(s>0)空间中研究了Camassa-Holm-Kadomtsev-

Petviashvili(CH-KP)方程

(ut-uxxt+κux+3uux-(2uxuxx+uuxxx))x+

uyy=0

解的局部适定性、爆破准则和刘维尔定理等。关于CH-KP方程的详细理论可参考文献[10-11]。

受文献[8] 和文献 [9] 的启发, 本文研究了二维广义Camassa-Holm-Kadomtsev-Petviashvili (CH-KP)方程

uyy=0。

(3)

其中：u(t,x,y)表示t时刻的流体速度；g(u)∈C∞(),g(0)=0；常数γ>0。方程(3)也称为Kadomtsev-Petviashvili(KP)方程, 其CH对应项是二维广义超弹性杆波动方程。本文的研究思路主要来源于文献 [9], 创新之处在于推广了文献 [9] 的研究思路及其方法的适用性, 研究得到了当g(u)∈C∞,γ>0时, 广义CH-KP方程(3)解的局部适定性结果。

首先, 将广义CH-KP方程(3)转化为等价形式。令uy=vx, 则uyy=(vy)x。进而可以将方程(3)写成下列等价形式:

(4)

(5)

G*vy=0

(6)

从而,将方程(3)转化为

(7)

考虑到方程组(7)的结构, 下面给出Xs(s>0)空间的定义及其内积和范数, 关于其详细内容可参考文献 [9]。

定义1Xs是一个希尔伯特空间, 其中s>0,

Hs(2), ∂xu∈Hs(2)}。

并对于任意u∈Xs(2)赋以范数

和内积

(∂xu,∂xv)Hs, ∀u,v∈Xs(2),

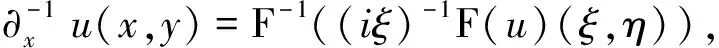
下面给出本文的主要结论。

定理1设u0∈Xs(2),s≥2, 则存在T>0, 使得方程组(7)在空间C([0,T];Xs(2))∩C1([0,T];Xs-2(2))中存在唯一解u，满足

此外, 解u连续依赖于初值u0。

定理2(爆破准则)设s≥2,u0∈Xs(2)且u是定理1中方程组(7)的相应解。假设是最大存在时间, 且g(u)=u3或g(u)=u4时, 有

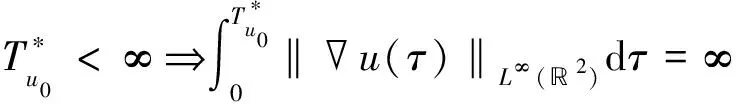
(8)

注记2局部适定性结果 (定理 1) 和爆破准则 (定理 2) 也对Sobolev空间Xs(Ω1×Ω2)，s≥2成立, 其中Ω1和Ω2是实数轴或单位圆P=/。

定理3假设u0∈Xs(P2),s≥2。设T0是方程组(7)在空间C([0,T];Xs(P2))∩C1([0,T];Xs-2(P2))中的解u的最大存在时间。当g(u)=ξγu2(ξ为任意常数)时, 假设有一点x0∈P满足

(9)

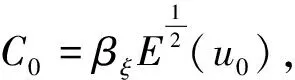
T0≤

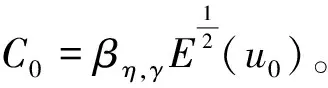
如果y∈, 则空间L2()不能嵌入到空间L1()中，定理3不成立。 通过给方程(7)乘以权函数, 得到了如下定理 4。

定理4固定φ∈H2(),φ≥0, 且假设u0∈Xs(2)，s≥2。设T0是方程(7)在空间C([0;T];Xs(2))∩C1([0;T];Xs-2(2))中的相应解的最大存在时间。当g(u)=un(n=3或4)时, 假设有一个点x0∈使得其中C2满足

则解u在有限时间T0内爆破,满足

注记5本文中的常数C0不一定相等，常数C也不一定相等。

研究中的主要困难是：①将文献[9]中的函数2κu+3u2推广到任意C∞函数g(u), 以及将2uxuxx+uuxxx项的系数1 推广到任意正数γ, 这将会增加方程的研究难度。受文献 [12-14]的启发, 找到g(u)的范数与u的范数之间的关系, 同时利用卷积的Young不等式和Sobolev嵌入等理论解决了主要困难。②一般的g(u)的范数与u的范数的关系式对爆破准则及其相关定理的证明不再适用。主要原因在于g(u)的范数估计式对函数u的正则性要求较高。因此, 在爆破准则及其相关定理中, 本文只论证g(u)为几类特殊多项式函数的情况。

1 预备知识

为了便于后面局部适定性定理的证明,给出以下几个引理。

‖fg‖Hs(2)≤C(‖Λsf‖Lp1(2)‖g‖Lq1(2)+

‖Λsg‖Lp2(2)‖f‖Lq2(2)),

其中p1,p2∈[2,+∞)和q1,q2∈(2,+∞]满足

i) ‖[Λs,f]g‖L2(2)≤

C(‖Λsf‖L2(2)‖g‖L∞(2)+

ii) ‖[Λs,f]g‖L2(2)≤

C(‖f‖Hq0(2)‖g‖Hs-1(2)，∀q0>1,

0≤s≤q0+1，

其中所有常数C与f和g无关。

引理3(Sobolev嵌入)[9]对于s≥2, 空间Xs(2)可以连续嵌入到Lip(2)空间中, 即存在一个常数C，使得‖u‖L∞(2)≤C‖u‖Xs(2)。

推论1[9]对于所有u∈Xs(2),s≥2, 则下列3个不等式成立:

iii) ‖u‖L∞≤C(‖u‖L2+‖ux‖L2+‖uy‖L∞)。

注记6在推论1中，所有C皆为正常数，且i)、ii)、iii)中的常数C不一定相等。

引理4[12]设g是上的光滑函数且g(0)=0。若u∈Hs(2)∩L∞(2),s>0, 则复合函数g∘u也属于Hs(2)∩L∞(2)空间, 并且有

‖g∘u‖Hs≤C(g′,‖u‖L∞)‖u‖Hs。

引理5[12-14]若u∈L∞(2), 则复合函数g′∘u,g″∘u也属于L∞(2)空间, 并且满足

‖g′∘u‖L∞≤

C(g′,‖u‖L∞)(1+‖u‖L∞),

‖g″∘u‖L∞≤

C(g″,‖u‖L∞)(1+‖u‖L∞),

其中,g是上的光滑函数且g(0)=0。

2 定理1的证明

定理1的证明分为存在性和唯一性两部分。由于其证明较为冗长, 所以先给出先验估计, 即论证命题1, 其证明主要分两大步:第一步对u作L2范数估计; 第二步对u作高阶Xs范数估计。下面给出先验估计及其详细的证明过程。

命题1(Xs能量估计)设u0∈Xs(2),u是方程组(7)的光滑解, 则有:

i)当s>2时, 下列估计式成立

且存在T>0,满足2C(γ,g′,‖u‖L∞)(‖u0‖Xs+1)T≤1,使得

2‖u0‖Xs, ∀t∈[0,T]。

ii) 当s=2时, 下列估计式成立

C(γ,g′,g″,‖u‖L∞)[(‖u‖L∞+

且存在T>0,满足

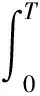
证明第1步 对u作L2范数估计。

vy=0。

(10)

方程(10)关于u作L2内积, 由分部积分得

(11)

接下来, 对等式(11)的右边两项分别估计。利用分部积分并整理可得

由分部积分与函数g(u)的光滑性可知

结合上述事实, 可以推出

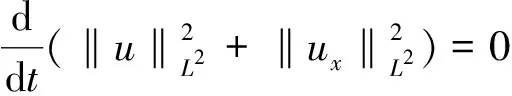
(12)

第2步 对u作高阶Xs范数估计。

对方程(10)变形并作用分数阶算子Λs, 有

∂tΛsu-∂tΛsuxx+

Λs∂yv=0

(13)

(14)

(15)

其中,Ai,i=1,…,4分别如下:

下面,对等式(15)右边的A1～A4分别进行估计。结合等式uy=vx与分部积分, 有

引理1, 计算出

Cγ‖u2‖Hs‖ux‖Hs≤

同理可得

将A1～A4的估计代入等式(15)并整理可得, 对于s≥2，

C(γ,g′,‖u‖L∞)(1+‖u‖L∞+

(16)

再结合Xs范数的定义,可推导出

C(γ,g′,‖u‖L∞)(1+‖u‖L∞+

(17)

情形1当s>2时，对式(13)关于Λsu在全空间作L2内积得

(18)

采用相似于A1的估计方法, 易得

|B1|=

C(γ)[C(g′,‖u‖L∞)+

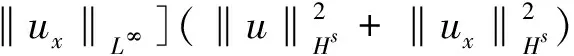
(19)

为了得到B2的估计,首先根据分部积分和交换子的定义得到

‖[Λs,u]uxx‖L2‖ux‖Hs)≤

C(‖ux‖L∞‖ux‖Hs+‖u‖L∞‖uxx‖Hs-1+

‖uxx‖L∞‖u‖Hs)‖ux‖Hs

(20)

再结合嵌入不等式和Young不等式可得

|B2|≤C(γ)(‖u‖L∞+

因此, 将B1至B3的估计代入式(18)并整理, 有

C(γ,g′,‖u‖L∞)(1+‖u‖L∞+

(21)

将式(17)和式(21)合并整理得

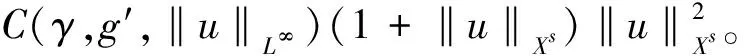
(22)

情形2当s=2时,空间Hs-1不能嵌入到空间L∞中，式(21)中的‖uxx‖L∞不能再利用嵌入不等式估计。因此, 对于s=2, 需要采用新的方法对u进行高阶导数估计。受文献 [9] 的启发, 并由推论1可知

(23)

‖uxx‖L∞≤C(‖uxx‖L2+

‖uxxx‖L2+‖uxxy‖L∞)。

(24)

∂tu+γu∂xu+γuxu+

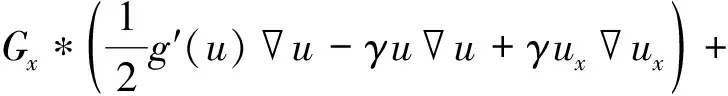
G*vy=0,

(25)

∂tux+γu∂xux+γuxux+

Gx*vy=0,

(26)

∂tuxx+γu∂xuxx+2γuxuxx+

2γuxxux+γuxxxu-

γuxu+γuux+

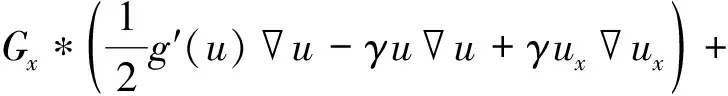
Gxx*vy=0。

(27)

I1+I3+I4+I6,

(28)

(29)

这里,Ij,j=1,…,7,分别是

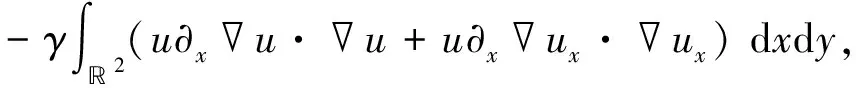
γuxux)]·uxdxdy,

γuu+γuxux)]·uxxdxdy,

继而对I1～I7分别进行估计。根据分部积分以及函数G的性质可得

|I3|≤(γ‖ux‖L2‖u‖L∞+

γuxux)‖L2)‖u‖L2。

(30)

C(γ)(‖g′(u)‖L∞‖u‖L2+

‖u‖L∞‖u‖L2+‖ux‖L∞‖ux‖L2)≤

C(γ)[C(g′,‖u‖L∞)(1+‖u‖L∞)‖u‖L2+

‖u‖L∞‖u‖L2+‖u‖L∞‖ux‖L2]

(31)

结合式(30)～(31)与Young不等式可得

|I3|≤C(γ,g′,‖u‖L∞)[(1+

类似于I3的估计,可以推出

|I4|≤

|I5|≤[2γ‖ux‖L∞‖uxx‖L2+

γ‖uxxx‖L2‖u‖L∞+

γ‖ux‖L2‖u‖L∞+

γ‖u‖L∞‖ux‖L2+

γuxux)‖L2]‖uxx‖L2

(32)

采用文献[9]中, 引理3.3的证明方法可以推出

C(γ)‖ux‖L2‖uxx‖L2

(33)

由引理5易得

C(g″,‖u‖L∞)(1+‖u‖L∞)×

(34)

C(g′,‖u‖L∞)(1+‖u‖L∞)‖ux‖L2。

(35)

将式(33)～(35)整理代入不等式(32), 并结合Young不等式放缩, 有

|I5|≤C(γ,g′,g″,‖u‖L∞)×

[(1+‖u‖L∞)(1+‖u‖L∞)+

(36)

于是,联立估计式I1,I3,I4,I6并代入等式(28), 可得

C(γ,g′,‖u‖L∞)(1+‖u‖L∞+

(37)

将I1～I7所有估计式联立代入等式(29),整理得到

C(γ,g′,g″,‖u‖L∞)[‖ux‖L2+

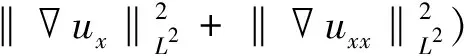
(38)

∂tuyy+γu∂xuyy+2γuyuxy+γuxuyy+

G*vyyy=0,

(39)

Gx*vyyy=0。

(40)

分别对式(39), (40)关于uyy,uxyy在全空间作L2内积并将所得结果相加, 得到

(41)

其中

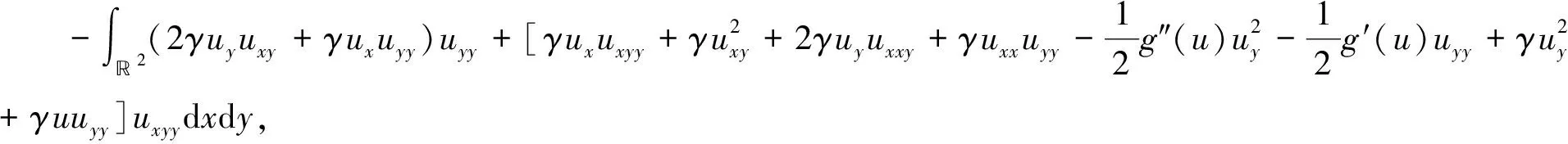
由分部积分, 函数G的性质以及uy=vx可得

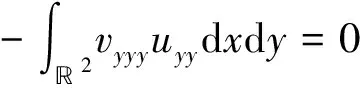
(42)

再次利用分部积分,对J2整理如下:

(43)

(44)

同理可得

(45)

C(γ)(‖ux‖L2+‖uxx‖L2)×

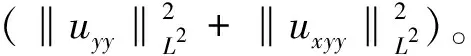
(46)

采用类似于式(44)的估计方法, 并结合引理5, 可推导出

‖uxyy‖L2≤

C(g″,‖u‖L∞)(1+‖u‖L∞)×

(47)

使用与推算式(47)同样的方法, 可以得到

C(g′,‖u‖L∞)(1+‖u‖L∞)×

(48)

将式(44)～(48)整理代入式(43), 适当合并可得

|J2|≤C(γ,g′,g″,‖u‖L∞)×

{[(1+‖u‖L∞)‖u‖L2+1+

‖u‖L∞+‖u‖L∞+‖ux‖L2+

[(1+‖u‖L∞)‖u‖L2+

于是,联立估计式J1～J4并代入式(41)可得

C(γ,g′,g″,‖u‖L∞)×

{[(1+‖u‖L∞)‖u‖L2+‖u‖L∞+

‖u‖L∞+‖ux‖L2+‖uxx‖L2+1]×

[(1+‖u‖L∞)‖u‖L2+

(49)

联立式(12)、 (16)、 (38)、 (49), 可推导出

C(γ,g′,g″,‖u‖L∞)[(‖u‖L∞+

(50)

一方面,当s>2时,易得

(51)

则式(51)结合式(22)可得

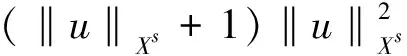
(52)

根据Grönwall[16]不等式计算可知

(53)

取T>0, 使得不等式2C(γ,g′,‖u‖L∞)(‖u0‖Xs+1)T≤1成立, 则根据bootstrap方法得到

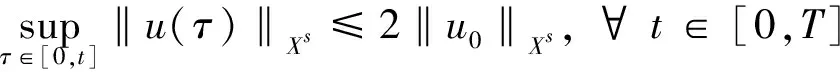
(54)

另一方面, 当s=2时, 有

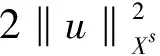
(55)

于是,式(55)结合式(50)易得

C(γ,g′,g″,‖u‖L∞)[(‖u‖L∞+

(56)

由Grönwall不等式可得

(57)

取T>0, 使得不等式

2C(γ,g′,g″,‖u‖L∞)×

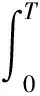
(1+‖u‖L∞)+

成立, 则由bootstrap方法得到, 式(54)仍然成立。

至此, 完成命题1的证明。

定理1的证明由命题1可知, 式(54)对∀s≥2都成立。再结合方程(3), 可以得到

∀t∈[0,T]

(58)

继而可以利用逼近方法[17]与紧性理论, 通过构造方程(7)的逼近方程, 并找满足特定条件的逼近解, 对逼近方程取极限等步骤, 进而得到解的存在性。

接下来, 证明解的唯一性。假设u(1),u(2)是方程(7)在空间C([0;T];Xs(2))∩C1([0;T];Xs-2(2))中具有相同初值的两个解。记δu=u(1)-u(2),δv=v(1)-v(2),则(δu,δv)满足

(59)

首先, 取方程(59)和δu的L2内积得:

(60)

(61)

(1-θ)u(2))(u(1)-u(2))]δudxdy|≤

C(g′,‖(u(1),u(2))‖L∞)(1+

(62)

其中θ∈(0, 1)。 又由分部积分与等式uy=vx, 易得

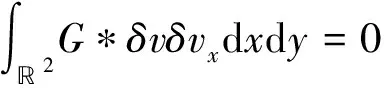
(63)

接下来估计D3。易知

(64)

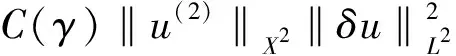
(65)

u(2))δu]δudxdy|≤

(66)

利用分部积分,卷积的Young不等式与引理3, 可得估计式

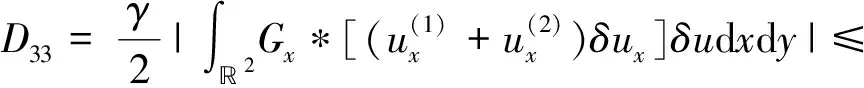
‖δu‖L2≤

(67)

将式(65)～(67)代入式(64), 适当合并可得

(68)

将式(61)～(63), 式(68)代入等式(60)得到:

C(γ,g′,‖(u(1),u(2))‖L∞)(1+

(69)

(70)

其中

(71)

(72)

(73)

继而估计E2。

(74)

(75)

C(γ)(‖(u(1)+u(2))‖L∞‖δu‖L2+

‖u(1)+u(2)‖L∞‖δu‖L2)‖δu‖L2≤

(76)

关键是估计E2,3。利用分部积分与卷积的性质,整理得到

(77)

(78)

(79)

将式(78)～(79)代入式(77)可知

(80)

将式(75)、(76)、(80)代入等式(74)可得估计式

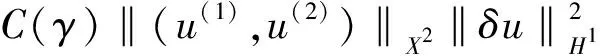
(81)

(1-θ)u(2))δuu(2)]·δudxdy|≤

C[C(g′,‖u(1)‖L∞)+

C(g″,‖(u(1),u(2))‖L∞)‖u(2)‖X2]×

(82)

由分部积分易得

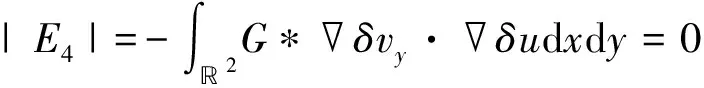
(83)

将式(73), (81)～(83)代入式(72), 有

C(γ)[1+C(g′,‖u(1)‖L∞)+

C(g″,‖(u(1),u(2))‖L∞)‖u(2)‖X2]×

(84)

于是,式(69)与式(84)联立可以推出:

C(g′,‖(u(1),u(2))‖L∞)+

C(g″,‖(u(1),u(2))‖L∞)‖u(2)‖X2]×

(85)

因此, 方程组(7)在空间C([0,T];Xs(2))∩C1([0,T];Xs-2(2))中存在唯一解u。此外, 根据式(54), 可以证明解u在空间Xs中连续依赖于初值u0。定理1证毕。

3 定理 2的证明

定理2的证明和文献 [9] 的爆破准则证明思路相同, 但证明过程更为复杂。为使问题简单化, 本文只论证g(u)=u3和g(u)=u4的情况。

情形1g(u)=u3。先验估计的证明思路与命题1类似, 因此只给出不同部分的推算过程。为了证明的简单化, 只证明s=2的情况。根据命题1可得

其中A1,A3,A4的估计与命题1相同。当g(u)=u3时,

C(‖u0‖L2,‖u0x‖L2)(‖u‖L2+

则对于s≥2，

C(‖u0‖L2,‖u0x‖L2,γ)(1+‖u‖L∞+

(86)

C(γ)‖u‖L∞‖ux‖L2‖u‖L2≤

C(‖u0‖L2,‖u0x‖L2,γ)(‖u‖L∞+1)×

对I4的估计采用类似于I3的证明方法, 可以推出

|I4|≤C(‖u0‖L2,‖u0x‖L2,γ)×

接下来估计

γuxu+γuux+Gx*

γuxux)]·uxxdxdy|。

C‖u‖L∞‖u‖L4‖ux‖L4‖uxx‖L2≤

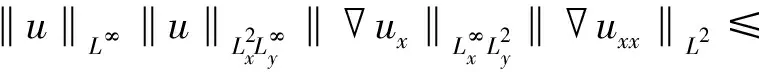
C‖u‖L∞(‖u‖L2+

C(‖u0‖L2,‖u0x‖L2)(‖u‖L∞+1)×

结合上述两个不等式, 就有

|I5|≤C(‖u0‖L2,‖u0x‖L2,γ)[(‖u‖L2+

于是,联立估计式I1,I3,I4,I6可得

C(‖u0‖L2,‖u0x‖L2,γ)(‖u‖L∞+1)×

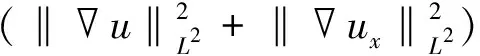
(87)

将I1～I7所有估计式联立并整理得到

C(‖u0‖L2,‖u0x‖L2,γ)[(‖u‖L2+1)×

(88)

(89)

从而,联立式(88)和式(89), 有

C(‖u0‖L2,‖u0x‖L2,γ)×

(90)

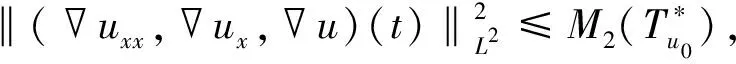
(91)

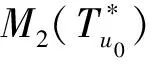
exp{C(‖u0‖L2,‖u0x‖L2,γ)×

接下来估计J1～J5。如命题1的证明, 易得J3=J4=0。关键是估计

γuuyy]uxyydxdy。

类似于式I5的估计方法,可推导出

C(‖u0‖L2,‖u0x‖L2,γ)×

(92)

使用与式(92)同样的方法, 可以得到

C(‖u0‖L2,‖u0x‖L2,γ)(‖u‖L2+1)×

(93)

将式(92)～(93)代入式J2, 整理得

|J2|≤

C(‖u0‖L2,‖u0x‖L2,γ){[(‖u‖L2+1)×

于是,联立估计式J1～J4可得

C(‖u0‖L2,‖u0x‖L2,γ)×

(94)

将式(12),(86),(88),(94)联立可推导出

C(‖u0‖L2,‖u0x‖L2,γ)×

将估计式(91)代入上式, 有

C(‖u0‖L2,‖u0x‖L2,γ)×

其中,

情形2g(u)=u4。先验估计的证明思路与命题1类似, 因此只给出不同部分的推算过程。为了证明的简单化, 只证明s=2的情况。根据命题1可得

其中A1,A3及A4的估计与命题1相同。当g(u)=u4时,

利用乘积估计迭代可得

(95)

再结合推论1与式(12)可得

(96)

则有

C(‖u0‖L2,‖u0x‖L2,γ)(‖u‖L∞+1)×

(97)

γuu+γuxux)]·udxdy|≤

C(‖u0‖L2,‖u0x‖L2,γ)(‖u‖L∞+1)×

(98)

类似可得

|I4|≤C(‖u0‖L2,‖u0x‖L2,γ)×

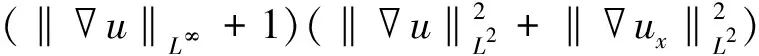
(99)

接下来估计

γuxxxu-6u2uxu-2u3ux+

γuxu+γuux+Gx*(2u3u-γuu+

γuxux)]·uxxdxdy|

(100)

由推论1可以推出

(101)

C‖uy‖L∞‖ux‖L2‖u‖L2‖ux‖L2‖uxx‖L2≤

(102)

所以

|I5|≤C(‖u0‖L2,‖u0x‖L2,γ)×

(103)

则有

C(‖u0‖L2,‖u0x‖L2,γ)(‖u‖L∞+1)×

(104)

‖u0x‖L2,γ)(‖u‖L∞+

(105)

(106)

C(‖u0‖L2,‖u0x‖L2,γ)[‖u‖L∞+

(107)

(108)

其中

exp{C(‖u0‖L2,‖u0x‖L2,γ)×

接下来估计

由推论1与式(12)可得

‖uy‖L∞‖uxyy‖L2≤

‖uy‖L∞‖uxyy‖L2≤

(109)

C‖uy‖L∞‖ux‖L2‖u‖L2×

‖uyy‖L2‖uxyy‖L2≤

C(‖u0‖L2,‖u0x‖L2)‖u‖L∞×

(110)

其他项如命题1中的估计,因此得到

|J2|≤C(‖u0‖L2,‖u0x‖L2,γ)×

(111)

所以

C(‖u0‖L2,‖u0x‖L2,γ)×

(112)

联立式(12)、(97)、(105)及式(112), 并利用式(108), 有

C(‖u0‖L2,‖u0x‖L2,γ)×

C(‖u0‖L2,‖u0x‖L2,γ)×

(113)

根据Grönwall不等式计算可知, 对所有t∈

其中，

4 定理 3和定理 4的证明

为了证明定理3,引入以下引理。

引理6[9,18]设u∈H1(P)。对任意α,β∈, 下面的卷积估计式成立

I(α,β)u2(x), ∀x∈P

(114)

其中I(α,β)是最佳常数,

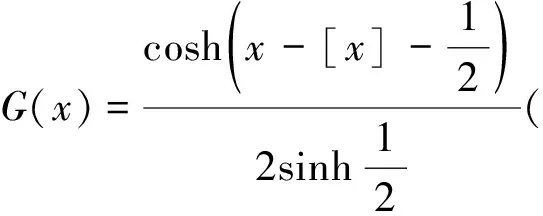
βα=inf{β∈ (0,+∞)|β2+

I(α,β)-α≥0}。

关于卷积估计的更详细理论, 读者可参考文献[18]。

4.1 定理 3的证明

对方程(7)关于y在 [0,1] 上积分可得

(115)

对方程(7)关于x求导, 然后在[0,1]上关于y积分可得

(116)

设q(t,x,y)是粒子轨迹, 定义为

γu(t,q(t,x,y),y),q(0,x,y)=x

(117)

则有

(118)

以及

(119)

定义两个关于时间t的函数如下:

ux(t,q(t,x0,y),y)dy,

(120)

ux(t,q(t,x0,y),y)dy。

(121)

直接计算可得

(122)

则有

(123)

当g(u)=ξγu2时,根据引理6和βξ的定义可得

(124)

(125)

u0x(x0,y)dy>0

(126)

(127)

(128)

(129)

(130)

关于时间在[0,t]上积分可得

(131)

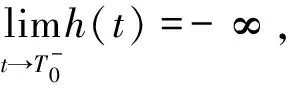
T0≤

<∞。

故定理 3得证。

注记3的证明g(u)=ηu2与g(u)=ξγu2的证明思路类似。因此, 只给出相异部分的计算。利用引理6和βη,γ的定义可得

(132)

(133)

推论2[9]假设初值u0满足定理 3或注记 3中的条件。设T0是相应解的爆破时间,T0>0。则可以得到在T0时刻的爆破率满足

(134)

证明∀ε>0， 对于∀t∈ (T0-ε,T0), 由定理 3 的证明可得式(129)以及式(130)。 对式(130)关于时间在[t,T0]上积分可得

(135)

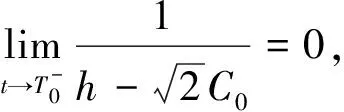
(136)

4.2 定理 4的证明

对式(7)关于x求导, 在等式两端乘以φ(y), 然后关于y在上积分, 可得

(137)

(138)

所以

(139)

γE(u0)‖φ‖L∞

(140)

(141)

将各项估计式代入式(138), 则有

(142)

(143)

所以存在一个时间T满足