覆冰架空导线舞动跳闸概率计算新方法

刘辉，马增泰，林济铿，田宏强，严波，左晨亮

(1. 国网安徽省电力有限公司，安徽 合肥 230022；2. 同济大学 电子与信息工程学院，上海 200092；3. 安徽继远软件公司，安徽 合肥 230031)

0 引言

目前关于覆冰导线舞动的研究主要集中在2方面：舞动机理与模型的研究和基于线性化思想的舞动故障预警研究。

（1）舞动机理与模型方面的研究有纵向的垂直舞动机理[6]、扭转舞动机理[7]等。覆冰导线舞动的模型主要包括单自由度、两自由度以及三自由度舞动模型[8]，采用增量谐波法[9]、矩阵摄动法[10]、牛顿定理法[11]及一维或多维的有限单元法[12-13]等。文献[14]利用达朗贝尔原理建立了覆冰导线的单自由度与两自由度舞动模型。文献[12]提出了基于牛顿法的单自由度舞动模型及慢变参数法求解策略，方法较为简单，但只适用于较小幅值的舞动情况。文献[15]提出了基于哈密尔顿原理的导线三自由度舞动模型及Newmark方法结合Newton-Raphson的求解策略，三自由度舞动模型较为精细，模拟舞动过程的精度高，但也较为复杂且需要信息较多，只能得到导线舞动形态的数值解。尽管不同模型均得到大家的研究及关注，但是相对于三自由度模型而言，单自由度模型简单且可方便地得到舞动幅值的解析解。再者，由于分裂导线已普遍应用于高电压等级的输电线路，而分裂导线的间隔棒在一定程度上能够限制导线的扭转，使得不考虑导线扭转的单自由度舞动模型更加贴近工程实际。

（2）基于线性化思想的舞动故障预警研究。其基本思想是先计算出导线舞动幅值，然后与相间距离进行比较得到以舞动幅值为自变量的线性化的跳闸概率。文献[16]提出了一种基于支持向量器和机器学习分类器的架空线路舞动跳闸预警方法。通过挖掘历史上易发生舞动区域的气象数据，构建了基于支持向量机（SVM）分类器的易舞动气象预报模型，得到舞动跳闸概率。文献[17]采用拉力传感器信息及覆冰导线实时水平荷载估算出导线舞动幅值，然后与相间电气距离比较，得到舞动跳闸概率。文献[18]基于现场舞动点的温度和湿度对舞动幅值进行实时预测，并进而得到跳闸概率。文献[19]基于拉力传感器与角度传感器得到覆冰导线张力与风攻角，由此推出导线舞动的幅值，并进而得到跳闸概率。不难看出，气象预测信息结合导线覆冰运动方程获得导线在下一阶段的预测跳闸概率已经受到了研究者的重视，但成果还比较有限，有必要进行更为体系化研究，从而获得更为准确的跳闸概率。

针对上述研究，本文提出基于舞动运动方程、气象信息及故障信息相结合的导线舞动跳闸概率计算新方法。该方法以贝叶斯公式为核心，将覆冰导线舞动的越限概率分布函数与覆冰舞动跳闸的历史故障记录所获得的泊松分布函数相结合，获得舞动幅值越限条件下的覆冰导线舞动跳闸概率。基本过程为：由风速与冻雨量的历史样本获得风速与冻雨量的概率分布函数，然后根据牛顿定律建立覆冰导线单自由度舞动模型；进而采用里茨-伽辽金方法求解舞动模型，获得以风速和覆冰厚度为自变量的舞动幅值解析表达式；在此基础上，利用已获得的风速与冻雨量的概率分布函数，获得与二者为函数关系的覆冰厚度的概率分布函数，进而获得舞动幅值的概率分布函数；最终，利用贝叶斯公式获得舞动幅值越限条件下的覆冰导线舞动跳闸概率。

1 覆冰导线舞动幅值的概率模型

1.1 覆冰导线舞动的幅值表达式

图1中实线部分为D型覆冰导线，对于不同冰厚及形状，式（1）中的气动参数将随冰厚而变化。本文使用回归分析方法构建气动系数与冰厚rH间的函数关系：根据典型覆冰形状，通过Fluent仿真软件对覆盖不同冰厚的导线进行气动力模拟，获取相应的三次多项式气动系数曲线，然后对气动系数与冰厚rH进行回归分析，得到气动系数c1与c2关于rH的函数表达为

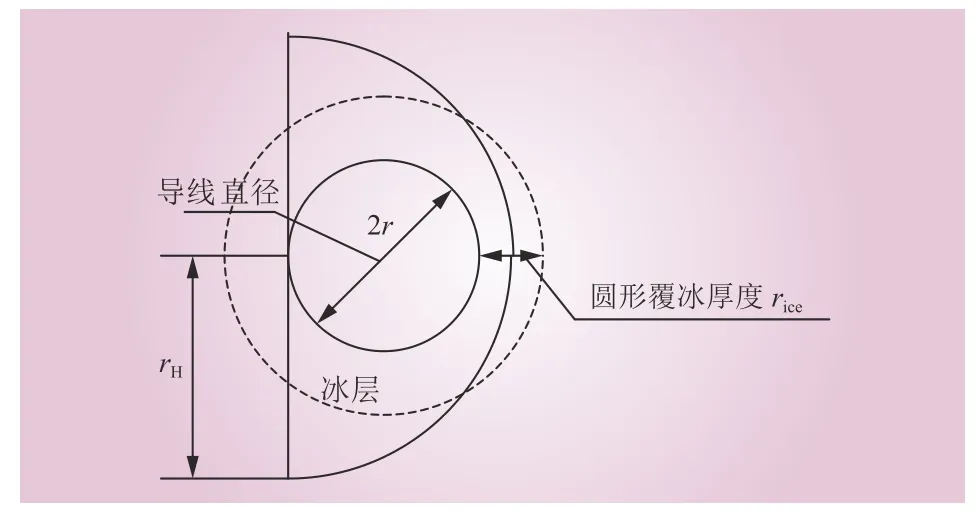
图1 覆冰导线截面Fig. 1 Cross-section of the D-type iced conductor

将式（9）代入式（8）可得覆冰导线舞动的幅值为

1.2 覆冰导线舞动幅值的概率分布函数

2 输电线路覆冰舞动跳闸概率

式中：cmax为导线不发生相间短路的最大舞动幅值，m。设导线静态相间距离为Lx，相间最小间距为Lxmin，两者都为已知量，单位都为m。对于图2所示垂直排列的三相导线，cmax为

4. Damballah, Ayida Wedo and the first of the other gods made the great city together.

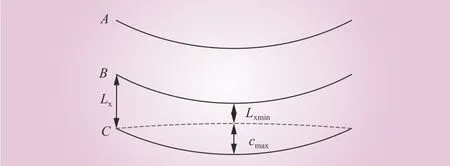
图2 导线垂直排列示意Fig. 2 Schematic diagram of vertical arrangement of conductors

对某待计算线路，其整体舞动跳闸概率由各档导线舞动跳闸概率逻辑串联而得到。

式中：i表示待计算线路第i档导线。

3 求解步骤

基于上述方法，本文所提出的覆冰输电线路的舞动跳闸概率计算方法流程如图3所示。其中覆冰风速、舞动风速与冻雨量的样本均值与样本峰度Kn为

图3 覆冰输电线路的舞动跳闸概率计算流程Fig. 3 Calculation flowchart of galloping-caused tripping probability of iced transmission lines

式中：Xi为覆冰风速、舞动风速或冻雨量的样本值。

当Kn≥3时，则选取使得值最大的Xi，并将其从样本中除去并重新计算样本均值与峰度；当Kn＜3时转选取剩下来的样本中最大的|Xi|为阈值。

需要指出的是，本文上述求解覆冰导线跳闸概率方法是以已有或预报的极端天气下风速与冻雨量样本以及历史故障记录为依据，并结合覆冰导线舞动方程而获得其最大的舞动距离幅值，而得到较为准确的舞动跳闸概率表达式（25）。文献[17-19]中依靠历史数据或传感器的实时监测获取线路舞动信息，因为传感器不能监测未来时段的导线张力或加速度等，所以无法进行极端天气条件下未来一段时间内线路舞动跳闸概率的计算；而若仅以历史数据来预测未来时段的舞动信息，因没有考虑线路实际的状况而使得其准确性较差。

本文方法基于风速与冻雨量的预报信息及线路舞动方程来建立风速与冻雨量的概率密度函数，而这些信息既能通过已有的样本数据获取，也能通过未来时段的气象预报获取，并进而获得线路跳闸概率，相应克服了文献[17-19]方法不能进行极端天气下未来一段时间内线路舞动跳闸概率的准确计算，或计算准确差的缺点。

4 算例分析

本文对2019年2月遭受冰冻天气影响的安徽宣城地区的500 kV线路覆冰舞动短路跳闸概率进行了计算。为了对风速与冻雨量进行广义帕累托分布拟合，收集了2016−2019年同时段发生冰冻灾害期间内80个冻雨量数据与150个风速数据。由峰度法获得覆冰风速、舞动风速与冻雨量的阈值uv′，uv，ul分别为7.9，9.6，5.4。

使用Fluent软件对以rice为2 mm等距的0～26 mm冰厚的D型覆冰导线气动系数进行模拟。

图4中，设置右边界为速度入口边界条件，左边界为流出边界条件。完成网格划分后，将该网格文件导入Fluent模块中，采用适用于圆柱绕流的K-ω湍流模型，并在导线垂直方向设置升力监测器以获取当前冰厚与风攻角的覆冰截面升力系数。通过旋转覆冰导线截面可改变风攻角，本文对导线不同冰厚时的风攻角范围均设定为（−60°，+60°），以10°为增量。完成全部冰厚及风攻角的升力系数的计算后，先建立各冰厚条件下风攻角与升力系数的函数关系式，然后采用回归分析方法建立如式（9）所示的c1与c2的表达式。

图4 覆冰导线截面网格Fig. 4 Cross-section gridding of iced conductor

统计2016−2018年同时段该地区500 kV总线路数和档数以及舞动跳闸事故记录，计算得到泊松分布参数=0.427，然后由式（24）得到基于历史故障记录的输电线路覆冰舞动跳闸的概率P（A）=1−e−0.427=0.074 8。

2019年2月10—11日，冻雨持续时间6 h，舞动跳闸事故发生。根据本文方法，结合气象、线路走向等导线起舞判断因素[23-25]（如表1所示），获取各档导线参数并由式（25）计算山沥线、官沥线、官涓线等线路的各档舞动幅值越限条件下短路跳闸概率如表2所示。

表1 导线起舞判断因素Table 1 Factors for judging conductor galloping

表2 单档导线舞动跳闸率Table 2 The galloping-caused tripping rate of single-span conductor

对于不同线路，经式（25）计算得到各档线路Pi（A|B）后，由式（27）计算得到整条线路舞动越限跳闸概率PLs。各条线路的舞动越限跳闸率与实际跳闸记录的对比如表3所示。

表3 线路舞动跳闸率Table 3 Galloping-caused tripping rate of transmission lines

由表3可知，实际跳闸的线路，基于本文方法所算得的其跳闸概率大多数超过0.5，只有官涓5387线小于0.5，但也非常接近0.5，表明本文算得的跳闸概率是比较符合实际情况的，相应也证明了本文方法的有效性。

5 结论

本文提出了基于舞动运动方程、气象信息及故障信息相结合的导线舞动跳闸概率计算新方法。该方法的特点包括：（1）根据牛顿定律建立了覆冰导线单自由度舞动模型，采用里茨-伽辽金方法求解舞动模型，获得了以风速与覆冰厚度为自变量的舞动幅值解析表达式。（2）由风速与冻雨量的历史样本获得风速与冻雨量的概率分布函数，基于已获得的风速与冻雨量的概率分布函数，获得与二者为函数关系的覆冰厚度的概率分布函数，并进而获得舞动幅值的概率分布函数。（3）根据覆冰舞动跳闸的历史故障记录所获得的泊松分布求得覆冰导线舞动幅值越限及短路故障的联合概率，并结合贝叶斯公式而获得舞动幅值越限条件下的覆冰导线舞动跳闸概率。

实际历史算例表明本文算得的跳闸概率与实际跳闸线路，是比较接近的。因此本文方法具有应用于实际的潜力。