复杂地形风电场中风加速效应的实验研究
2022-04-19严晓生李岳高晓霞王喜
严晓生,李岳,高晓霞,王喜
(1. 福建国电风力发电有限公司, 福建 福州 350800;2. 华北电力大学 能源动力与机械工程学院, 河北 保定071003;3. 河北龙源风力发电有限公司, 河北 张家口 075000)
0 引言
随着风电产业的不断发展,陆上平坦地区风电场基本已开发殆尽,新建陆上风电场大多选址于复杂地形。复杂地形风电场风况变化复杂,地表粗糙度、山体坡度、风向等都会对风速产生一定的影响;除此之外,有效风速的利用时间、最频繁风速也是要考虑的因素。山地地形的存在会使得正常的平地来流在经过一定高度差后,产生大于来流风速的风,该现象即加速效应。针对坡地对风的加速效应影响,目前的主要方法是比较同一水平高度下平地风和山地风场的区别,多采用无量纲常数加速比来表征加速效果。
文献[1]最先阐述了风速在坡地上的变化,但其针对的对象为二维理想型山体,实用性较低;文献[2-5]提出了简化算法和分级加速比,这一改进使得计算精度大幅度提高,对地形带来的非均质流误差进行了校正,得出了加速程度与大气的稳定性的关系;文献[6-9]对山地平均风的加速效果做了数值模拟,研究了地貌因素起到的作用,探究了山体坡度、高度、长度、间距对风速分布的影响,提出了关于高度、坡度等因素的修正算法;文献[10]总结了复杂地形对低风速风场的影响,得出地形因素会导致风切变发生变化,使得风速大幅度减小,入流角和湍流强度也会受到复杂地形的影响,会使可利用风能减少以及机组载荷增大;文献[11-13]进行了大量的风洞或风场实验,并对风速进行了多尺度的CFD数值效应模拟,提出了针对二维地形、简单三维地形以及较复杂三维地形下的参数模型;文献[14-15]选择多种典型山地地形进行了数值模拟,对风加速效应的整体分布进行了分析,探讨CFD流体模拟应用于风电场选址的可行性;文献[16-18]对多种坡度的山体模型进行风速测试,对大气边界层湍流特性进行实验,研究了典型陡坡山体、山丘地形风场的三维特性,得出了地形,特别是地表粗糙度对大气边界层流动的影响规律。文献[19-21]利用数学方法推导了风加速效应的差值模型、指对数模型等,指出相关模型须依据实际工况中出现的多种因素进行系数修正,使得模型的精确度和线性相关程度大幅度提升;文献[22-24]将风加速效应的多种模型应用到了山地风电场的风资源评估及发电量计算中。
总的来说,已有研究多采用数值模拟和风洞试验的方法,其流场边界条件的设置、机组分布的设计较为单一或理想化,不能完全还原真实风场中复杂多变的地形条件。此外,缩尺试验还需要考虑尺度对实验结果的影响。本文采用风场实验的方法研究坡地地形,主要是高度、坡度、来流等多个因素对风加速效应的影响,并将Taylor原始算法在该地形下的计算结果与实验数据进行对比,分析产生误差的原因,给出适用于复杂风场地形的Taylor计算式的修正式。
1 实验设计
实验在华北地区某具有典型复杂地形的风电场进行,风场地形及风力机分布如图1所示。
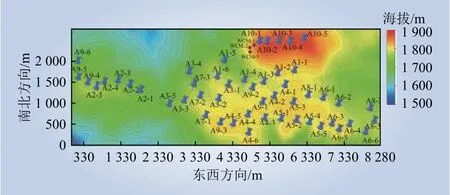
图1 实验风场Fig. 1 Experiment wind farm
实验选取风力机10-1所在的典型坡地为研究对象,并在此布置了3个测点,如图2a)所示。该坡地同周边相比海拔最高,地表起伏明显,地形复杂,能够反映典型复杂地形坡地的风加速效应。测点距其他风机有一定距离,尾流效应影响可以忽略。测风装置(见图2b))由风向标、风速仪、太阳能电池板、蓄电池以及无线网关组成,可以持续无间断地对风速风向进行测量,每分钟记录一次数据,并将数据传送至平台。3个测点在坡地上呈现三角形布置,WCM-3(3号测点)位于海拔最低点,WCM-1(1号测点)位于海拔最高点,3号测点与2号测点之间、3号测点与1号测点之间以及2号测点与1号之间分别构成了3个不同的坡度,当风向改变时通过测风数据可以得到不同地形的风加速情况。测点的相对位置数据见表1(其中连线风向表示风向恰好与两测点连线方向相同,采用16方位表示)。

图2 实验位置以及测风装置Fig. 2 Experiment location and measuring device

表1 测点距离Table 1 Distance between the measuring points
2 实验结果
Taylor原始算法[2,25]给出了不同位置处的加速比计算方法,即

式中:S为加速比;Smax为最大加速比;A、B为2个经验常数,根据山体几何条件不同而不同;h为坡顶的高度;L为坡地测点到坡底的地表距离;z为1/2坡地上测点的高度,如图3所示。
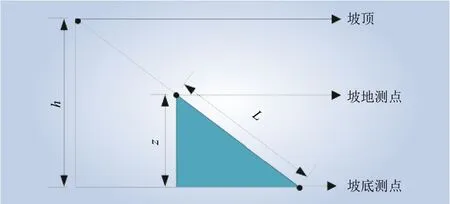
图3 地形参数定义Fig. 3 Definitions of terrain parameters
根据Taylor原始算法,获得实验风场地形参数如表2所示。
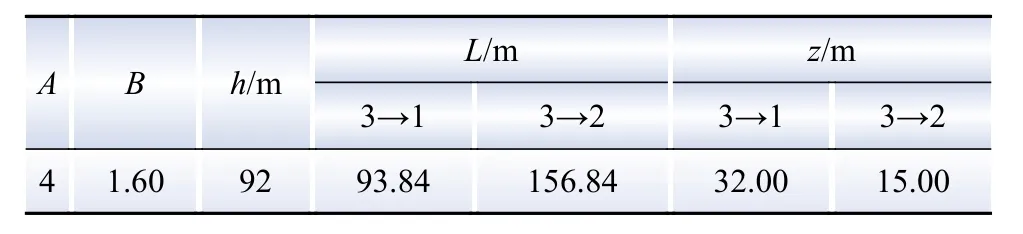
表2 实验风场地形参数Table 2 Terrain parameters of the experiment wind farm
将地形参数代入式(1)(2),得到

按照误差值不超过设定的最大值的方法,对数据进行筛选,获得3→1和3→2的风向基本相同的数据,即测点在来流的同一二维面上。由实验数据得到的加速比为

2.1 高度对加速效应的影响
保持来流高度相同,即均采用测点3的数据作为来流数据,将二维面3→1和3→2实测加速比与Taylor算法的结果进行对比,如图4所示。实测加速比在文献[13]中同条件下加速比的模拟结果附近波动,但是测点1处实际的风加速效应平均为预测值的16.5%,最大不超过37.1%,而测点2处实测结果的平均值与预测值相近,这说明了迎风面海拔更高位置的风加速效应并没有Taylor算法所描述的大,需要考虑坡度等其他因素的叠加影响。此外,实验中的加速比发生了较大的波动,这表明实际上复杂多变的地表对风加速效应产生了较大的影响。
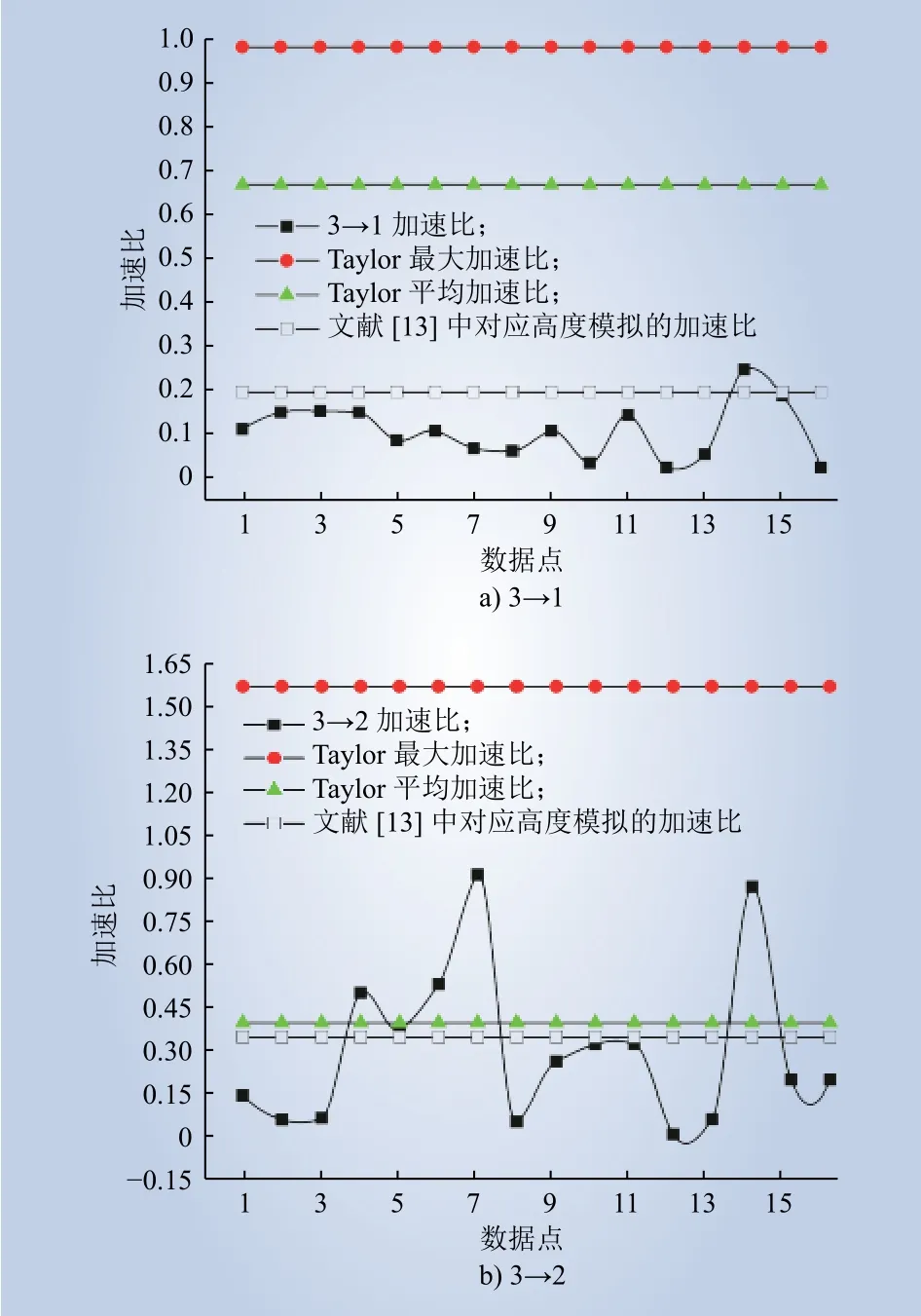
图4 实测加速比与Taylor算法加速比的偏差Fig. 4 Deviation between the actual acceleration ratio and the acceleration ratio calculated by Taylor algorithm
2.2 坡度对加速效应的影响
以测点1数据为坡地风速,将测点2和3数据分别作为来流风速,计算加速比,结果如图5所示。其中,二维面2→1坡度为48.99%,二维面3→1坡度为44.02%。可见,二维面2→1的加速效应比3→1更加显著。二维面2→1的加速比比3→1平均偏高61.6%,最大值达187.8%。这说明坡度对风的加速效应程度存在影响,坡度越大,加速效果往往更加显著。这一点同文献[13]中模拟结果所得趋势相同,但是,同高度同坡度的实测加速比较模拟结果略高,这主要是因为风场实测来流方向并不能和模拟条件完全相同。
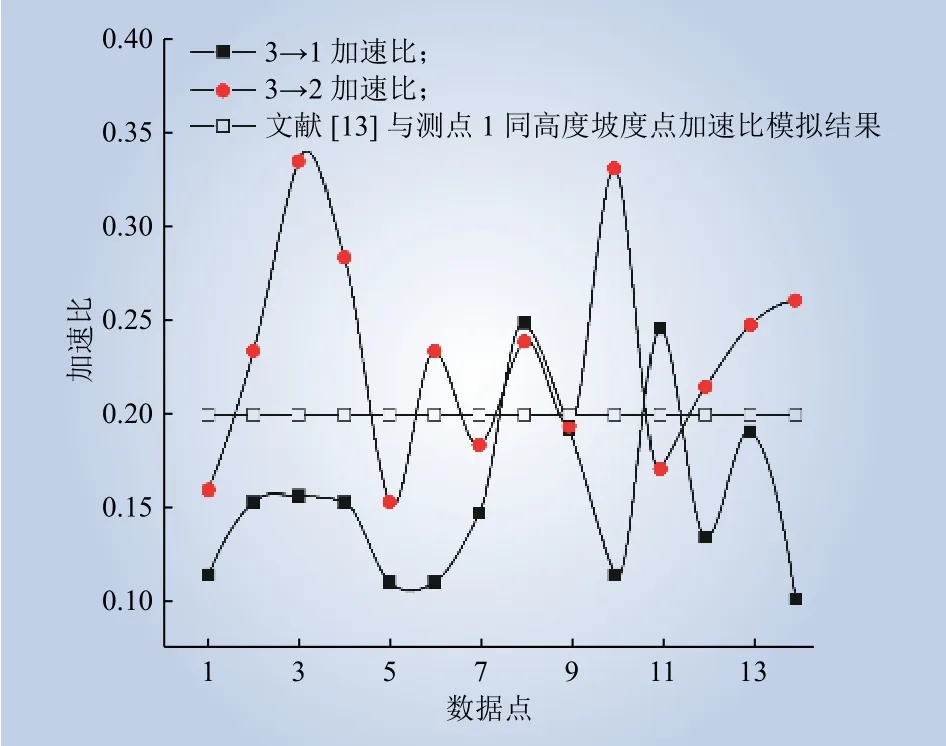
图5 二维面2→1和3→1的加速比对比Fig. 5 Comparison of acceleration ratios of 2→1 and 3→1
2.3 来流对加速效应的影响
迎风坡面和侧风坡面的划分如下:当测点1和3的风向和3→1基本相同时,则二维面3→1为迎风坡面,此时二维面3→2即为侧风坡面;同理,当定义二维面3→2为迎风坡面时,二维面3→1为侧风坡面。图6为迎风坡面的选择不同时,迎风坡面和侧风坡面的加速比。可以看出,侧风坡面的加速比整体上略大于迎风坡面,平均偏大8.9%~11.9%。这说明即使在同一来流下,不同坡面的加速比也不尽相同。

图6 迎风坡面与侧风坡面的加速比Fig. 6 Acceleration ratios on the windward and crosswind sides of the slope
图7为测点1和2的风速玫瑰图。测点1南部整体风速较大,其中西南方向以及东南方向较大;测点2北部风速极小,西南方向风速很大。整体来看,该山坡以南风为主,特别是西南方向来流风速普遍较大。虽然二者西南方向风速都较大,但是位于高处的测点1出现了东南方向的大风速,这表明了复杂地形不仅具有风加速效应,还可能改变风的方向,这也是Taylor计算式计算精度较差的原因之一。
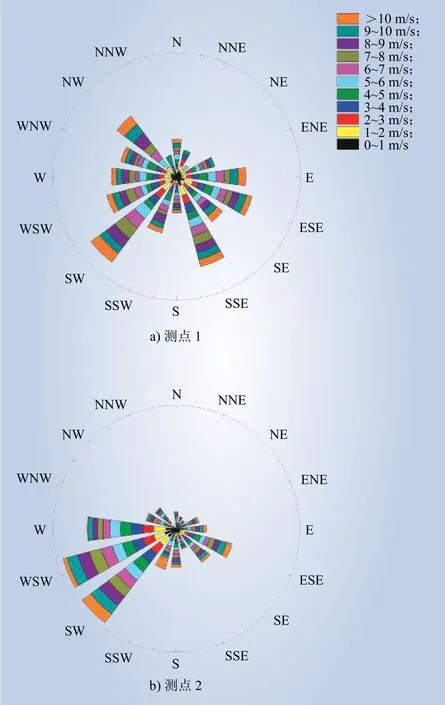
图7 风速玫瑰图Fig. 7 Rose diagram of wind speed
2.4 Taylor算法精确程度分析
对比发现,实验数据得出的加速比与Taylor计算式的结果相差很大,说明在不规则三维山体上,Taylor计算式的计算精度较差。由于地形复杂,不同来流处于地形不同的二维面上,加速效应也不尽相同,经验常数应该根据具体的地况做出调整。据此,提出Taylor加速比计算公式的修正式为
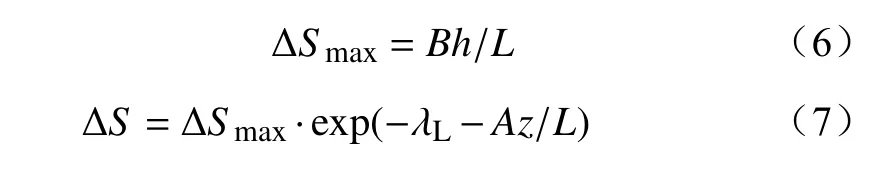
式中: λL为在三维不规则山体上,由不同二维面的坡度、地表粗糙度等因素决定的修正系数。本实验中,2个风向下的 λL的取值分别为1.640(二维面3→1)和4.342(二维面3→2)。
3 结论
本文采用风场实验的方法研究坡地地形对风加速效应的影响,分析了高度、坡度、来流对加速效应的影响,并将Taylor原始算法在该地形下得到的计算结果与实验数据进行对比,分析了产生误差的原因,得出结论如下。
(1)本实验中,高海拔时,实测加速比仅为Taylor原始算法预测的加速比的16.9%左右,并且加速比在同一风向上产生了较大的波动,这表明复杂多变的地表对风加速效应有很大的影响。
(2)在复杂地形风电场中,坡度较大的地形有更好的风加速效果,本实验中较大坡度处的加速比平均偏大61.6%左右。
(3)在复杂风场中,风的加速效应在迎风坡面和侧风坡面表现不同,本实验中侧风坡面的加速比比迎风坡面大10%左右。这表明了复杂地形不仅具有风加速效应,还可能改变风的方向。
(4)Taylor原始算法在三维不规则山体上的计算精度并不理想。这是因为,不同方向的来流处于不同的二维面上,各二维面上的地表情况不同,从而导致了加速效应不尽相同,此时,应该根据具体山体的地表情况添加修正系数。本文已给出对应的修正公式,可根据地况进行修正。
