基础实验试题A-2和A-3:毛细管中液体的流动及风洞实验
2022-04-19文小青李文华张旭华张春玲孔勇发
文小青,王 槿,李文华,张旭华,张春玲,孔勇发
(南开大学 a.物理科学学院;b.基础物理国家级实验教学示范中心,天津 300071)
伯努利方程中的基本假设是流体无黏性,而实际的流体都具有黏性. 对于液体,形成黏性的主要原因是分子间的引力,同时还受到温度影响. 而对于气体,形成黏性的主要原因是分子热运动引起的动量交换[1]. 测量流体的黏度是基础物理实验教学中的重要内容. 第7届全国大学生物理实验竞赛(教学赛)基础实验试题A的研究内容为流体的流动. 试题A共分为三部分:第一部分为水钟计时,第二部分为毛细管中液体的流动,第三部分为风洞. 其中第一和第二部分为“二选一”形式. 基础实验试题A涉及液体的静力学及表面张力现象、动力学(液体流动及黏性)和气体动力学(空气在风洞内的流动)等相关知识. 本文介绍的第二部分和第三部分都与流体的黏性有关.
1 实验原理
1.1 毛细管中液体的流动
当相邻2层流体以不同的定向速度运动时,如图1所示,由于流体分子的相互作用,产生平行于接触面的切向力,该力被称为内摩擦力或黏性力[2].经实验验证,对于给定的流体,作用于接触面积为dS的相邻两流层上的黏性力f,与垂直于dS方向上的速度梯度du/dy以及接触面积dS成正比,其方向与运动方向相反,即
(1)
其中,比例系数η为黏度.式(1)是决定流体内摩擦力大小的牛顿黏性定律.
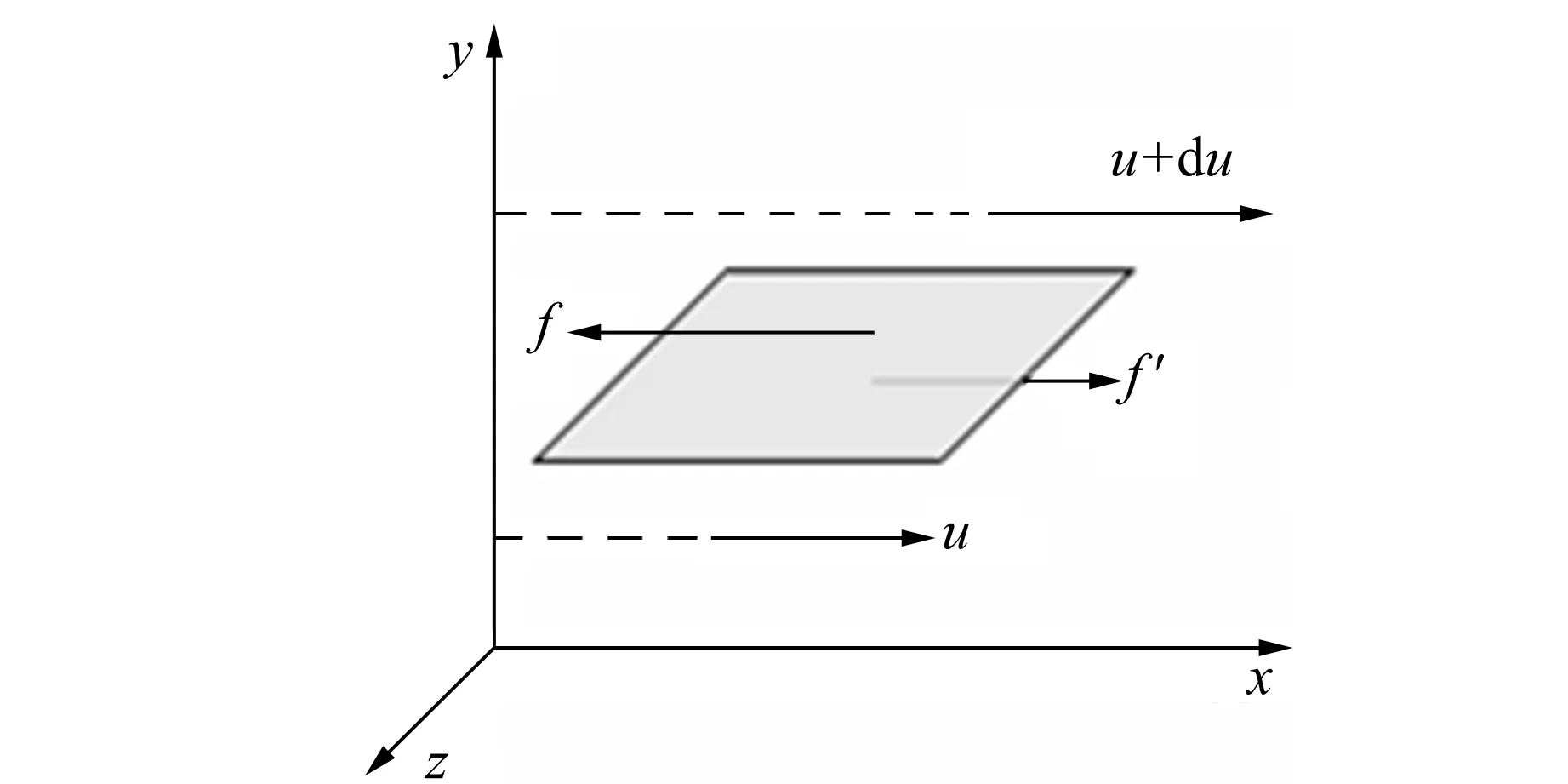
图1 流层间的黏性力
不同流体具有不同的黏度,同种流体在不同温度下的黏度也不同,而且流体的黏度还与压强有关,但不显著.气体的黏度很小,且与温度的平方根θ1/2成比例[1].液体的分子间距比气体的分子间距的1/1 000还小,层间分子的相互作用力成为产生内摩擦力的主要原因,所以液体黏度是气体的102~104倍.而且液体黏度随温度的升高近似呈指数规律减小,有经验公式
ηθ=a(b+θ)-c,
(2)
其中,ηθ为流体在θ℃时的黏度,a,b,c为因液体种类或温度范围而异的常量[3].对于实验中的液体,温度在0~100 ℃范围内时,式(2)计算结果与理论值的偏差不大于0.40%. 因此,由式(2)计算得到ηθ可以理想化为真值,用来验证实验结果.
流体的流动形态分为层流和湍流,可用雷诺数的大小来界定这2种流态.雷诺数是流体力学中表征黏性影响的无量纲量,由物体的特征长度决定,记作Re.
(3)
其中ρ,v和η分别为流体的密度、流速和黏度,D为特征长度[1].
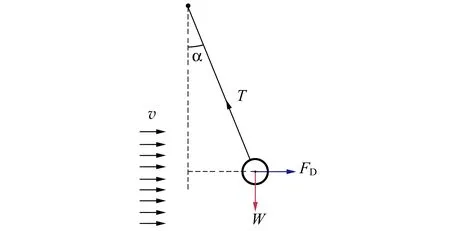
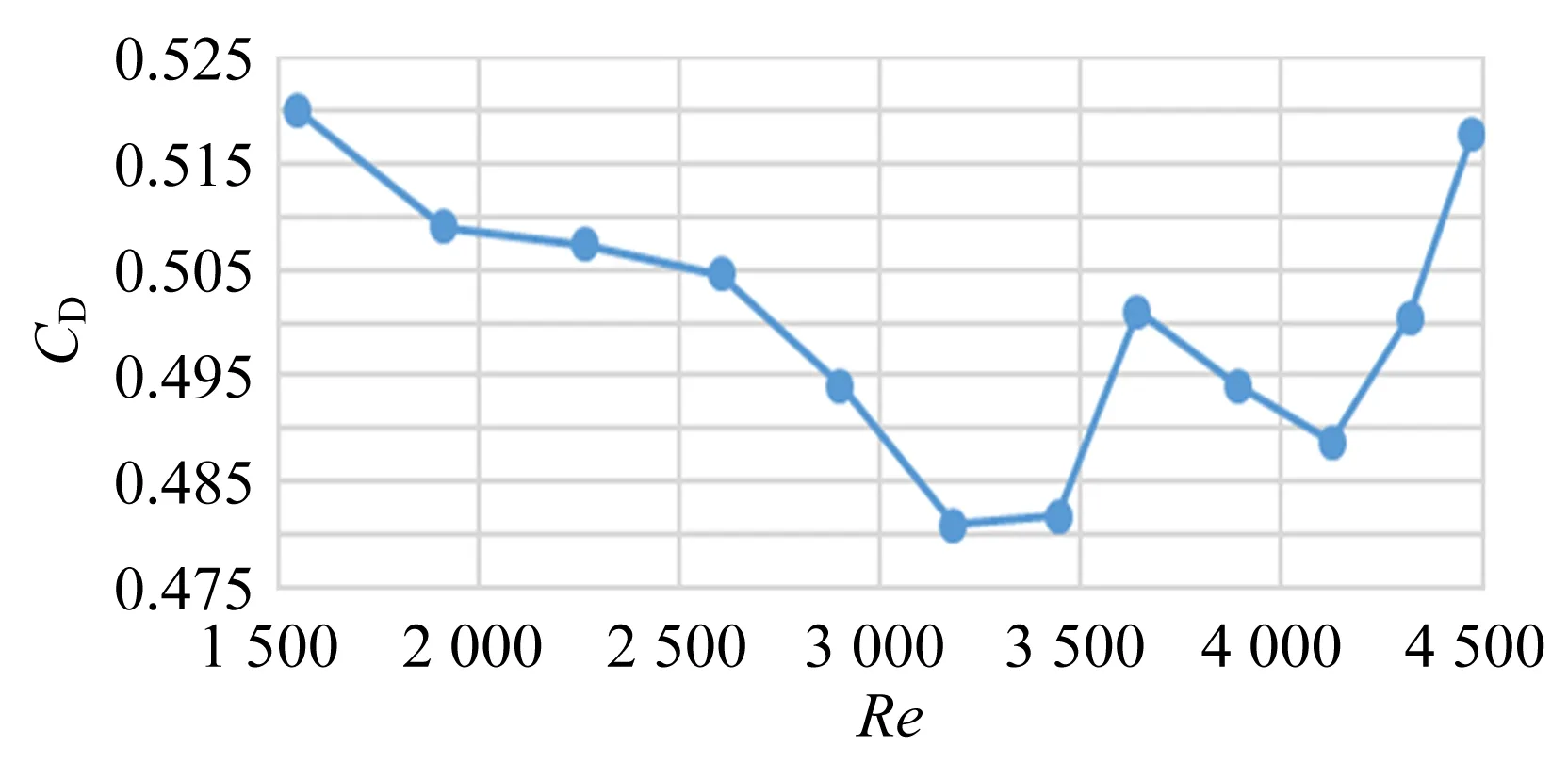
雷诺数的意义是流体的惯性力与黏性力之比.雷诺数较小时,黏性效应在整个流场中起主要作用,流动为层流;雷诺数较大时,紊动混掺起决定作用,流动为湍流.实验表明,对于内壁光滑的直管而言,Re<1 000时,为层流;Re>2 000时,为湍流;当1 000 测定流体黏度的方法有多种,例如毛细管法、旋转圆筒法、落球法以及观察阻尼振动法等[3].毛细管法测量液体的黏度主要依据牛顿黏性定律,如图2所示,当液体在长度为l、直径为D的毛细管中做层流运动时,可以证明t时间内流经毛细管任一截面的体积为 图2 毛细管中液体流动的受力分析 (4) 其中,Δp为毛细管两端的压强差.式(4)即为泊肃叶公式. 空气是常见的流体,空气的流动直接导致风的产生,风速的大小一般由风速计测量,市场上常见的风速计有热线式(热球式)、托管式、超声波式、风杯式等.实验试题中将乒乓球置于风洞,研究风洞内与空气流动的相关物理性质. 由于空气的黏性作用,当空气流动时会产生与物面相切的摩擦力,全部摩擦力的合力称为摩擦阻力.摩擦阻力与物面相垂直的气流压力的合力称为压差阻力.实际流体在黏性作用下不仅会产生摩擦阻力,而且会使物面压强分布与理想流体中的压强分布不同,并产生压差阻力,这2种阻力常同时存在,与物体的形状、物体的表面粗糙程度和雷诺数有关.阻力的方向与物体相对于流体的速度方向相反,其大小和相对速度大小有关[1].在相对速率v较小时,阻力f与v成正比,即f=kv(比例系数k取决于物体的大小、形状以及流体的性质);在相对速率v较大以至于在物体后方出现流体旋涡时,阻力可表示为[4] (5) 其中,ρA为空气密度,AB为物体的有效横截面积,CD为曳力系数(取决于物体形状和雷诺数). 第二部分:毛细管黏度计(图3)及毛细管小样一段. 图3 毛细管黏度计 第三部分:风洞装置(图4,含风洞管道主体、计算机风扇和光电传感器),系有细线的乒乓球1个(质量已标到球体上),双通道电源1台,示波器1台,热线式风速仪1台,黑色导线1根. 在设计风洞实验装置时借鉴了第14届亚洲物理奥林匹克竞赛试题[5]仪器的外观设计.数据采集电路、配件等由命题教师设计完成. 如图4所示,实验中,将计算机风扇作为风发生器,将风洞中的空气吸出(排风型风洞)以获得平缓的气流.风洞内的风速主要取决于计算机风扇的转动频率fM,fM可由风扇上装有的光电传感器来获得.光电传感器含有1对红外光发射器和接收器,根据涡轮扇叶上粘贴反光片的反射光信号周期来获得fM.赛场提供了商用的热线式风速仪,用来测量风速,以进行比对研究. 图4 风洞装置实物图 共用器材:移测显微镜1台,量程0~100 ℃的温度计1支,秒表1块,烧杯1~2个,铁架台1个,夹子若干,游标卡尺1把,含待测液体的洗瓶2个,刻度尺2把,透明胶带1卷,废液桶1个,LED照明灯1盏,抹布2块. 3.1.1 实验要求 1)如图3所示,假设计时开始时,毛细管黏度计量筒内液面高度为h1,计时结束时液面高度为h2,毛细管入口处的高度为h,毛细管出口处的高度为h0.液体流动过程中毛细管内的流量等于量筒内的流量[6]: (6) 2)将仪器调节到测量模式,通过测量50 mL液体流经毛细管的时间以及其他参量来获得液体的黏度,进行3次实验.(20分) 3)对于待测液体,设置式(2)中a=0.600 7,b=43.252,c=1.542 3.根据实验时的液体温度,求出3次实验中黏度的理论值,并与实验值相比较,计算相对偏差.3组实验数据中,选出相对偏差最小的1组,计算实验条件下的雷诺数,分析其是否满足泊肃叶公式的成立条件.(14分) 4)欲使该装置准确地测量待测液体50 ℃时的黏度[可通过式(2)求得],毛细管直径不得大于多少?(8分) 3.1.2 试题解答 1)此题考查学生对泊肃叶定律的理解和灵活应用. (7) 具体解答可参考文献[3]. 2)此题要求根据式(4)及式(7)测得液体的黏度,为增加实验的可重复性和准确性,要求重复进行3次实验.需要测量的参量和测量次数在答题纸中以表格形式给出.此处给出1组参考数据,如表1所示. 表1 毛细法测量液体黏度的数据记录 3)由式(2)计算黏度理论值,η01=0.881 1×10-3Pa·s;η02=0.883 1×10-3Pa·s;η03=0.883 1×10-3Pa·s. 相对偏差分别为:3.4%,8.4%,5.7%. 流速v可定义为体积流量除以毛细管横截面积,结合式(4)得雷诺数为 (8) 代入表1中相关数据,可得Re=100.8<1 000,满足泊肃叶公式成立的条件. 4)由式(2)可求出50 ℃时液体的黏度η02=0.550 6×10-3Pa·s.式(8)可改写为 (9) 要保持液体流动形态是层流,根据经验Re取值应小于1 000,由式(9)计算可知,此时毛细管直径D≤1.15 mm. 3.2.1 实验要求 1)如图5所示,密度为ρA、速度为v0的空气流过横截面积为A0的管道,空气流具有的功率为 通过推导确定n的数值.(5分) 图5 管状风流示意图 2)风洞内的风速与风扇的转动频率直接相关,而风扇的转动频率可由风扇的工作电压进行调节,请参考图6连接光电传感器及风扇电路,通过改变风扇工作电压测量风洞中心位置的风速与风扇转动频率的关系数据,以表格形式记录数据,并绘制关系曲线,通过数据拟合得到风速v0与风扇转动频率fM的关系表达式.(15分) (a)传感器电路 (b)风扇电路 图6 风洞工作电路图 3)如图7所示,在探究空气流动的物理性质时,可将乒乓球悬挂于风洞中测量风速的大小.风扇打开时,小球在风的作用下会偏向一边,假设此时丝线与竖直方向夹角为α,分析此时小球的受力并画出受力图.根据小球在流动空气中的受力与相关参量的关系,推导出风速v与小球偏移角α的函数关系(可申请提示卡).(10分) (a)风洞上的刻度 (b)小球悬于风洞中 (c)标有质量的小球 (d)风洞整体图图7 风洞 4)改变风速,测量乒乓球偏移角α,以表格形式记录实验数据.计算不同风速下的曳力系数CD及雷诺数Re.画出雷诺数与曳力系数的关系曲线,并分析该曲线图.(20分) 3.2.2 试题解答 1)设空气在管道内的速度不变.则 2)此题考查学生的动手实践能力.根据风洞工作电路图连接实验仪器,风扇转动频率可通过示波器直接读出.根据测量数据,可得到风扇转动频率与风速呈线性关系.因每个风扇的电机性能不同,风扇转动频率与风速的线性系数不是定值.经测试,竞赛中所用风扇转动频率与风速的线性系数在0.500~0.900之间. 3)乒乓球在风洞中的受力如图8所示,结合式(5),风速v与小球偏移角α的函数关系为 图8 风洞中小球的受力图 图9 雷诺数与曳力系数的关系曲线 因风扇的电机性能不同及悬挂乒乓球的位置略有不同,通过对每台风洞仪器测试,CD的值在0.40~0.90之间,Re的值在1 000~5 000之间,根据球体的曳力系数与雷诺数的变化关系[4,6],此雷诺数区间阻力系数曲线为整体趋于平稳或略有下降,实验结果与理论相符. 附录1:不同温度下的空气动力黏度及密度. 附录2:移测显微镜使用说明(JC-10,上光学仪器五厂). 附录3:热线式风速仪使用说明. 附录4:示波器使用说明. 附录5:双通道电源使用说明. 4.1.1 得分分布 基础实验试题A第二部分共4道题,总分50分. 参加考试的55名学生中有12人选择了第二部分. 总分分布如图10所示. 具体各题得分分布如图11所示. 图10 第二部分的总分分布 (a)第一题 (b)第二题 (c) 第三题 (d)第四题图11 第二部分各题得分分布 第一题涉及泊肃叶定律的理解,考查学生对泊肃叶公式适用条件的灵活应用,得分率较低,但不影响后面实验的进行. 5人申请了提示卡. 第二题是基础物理量的测量,得分率较高,学生得分都在10分以上. 第三题得分率较高,学生得分都在8分以上. 第四题属于实验拓展部分,得分率较低,学生得分都在3分以下. 4.1.2 结果分析 第二部分主要是利用倾斜的毛细管测量液体的黏度,通过毛细管中液体流动的物理状态与雷诺数的关系进行实验拓展. 在第5届全国大学生物理实验竞赛教师交流会上调查的40所高校中,21所高校采用落球法测量液体黏度,1所高校采用转筒法测量液体黏度. 选择第二部分的学生人数为12人,占比21.82%,这与大部分学校没有开设毛细管法测量液体黏度有关,学生没有相关内容的知识储备. 教材上一般给出水平毛细管两端的压强差公式,而此题要求计算倾斜毛细管两端的压强差,涉及对泊肃叶公式的理解和灵活运用,大部分学生不能推导出此公式. 实验背景中已经明确给出此装置适用于层流状态下黏度的测量,层流的临界雷诺数值和雷诺数公式也已给出,但大部分学生不能从实验背景中提取有用信息,第四题得分较低. 在仪器操作方面,大部分学生能利用提供的实验器材进行第二题中基础物理量的测量,这是此题的主要得分点,但学生使用仪器不够熟练,不能快速、有效地开展测量,导致做第三部分实验题的时间较少. 此外,学生也会犯原理性的错误,例如实验时未取下毛细管黏度计量筒上的橡胶塞. 4.2.1 得分分布 基础实验试题A第三部分共4道题,总分50分. 第三部分为必做题目,总分分布如图12所示,平均分33.3分. 各题得分分布如图13所示. 第一题考查学生对基础物理概念的掌握和灵活运用,题目相对简单,得分率较高,55名学生全部得满分. 第二题考查学生的实验动手能力,根据电路原理图连接实物并进行测量,一半学生的成绩在5分以下,仅有5名学生的成绩在12~15分,得分率不高. 第三题考查学生理论联系实际的实践能力,此题设计有提示卡,虽然得分率较低但不影响后面实验的进行. 第四题属于实验拔高部分,是试题的难点部分,得分率较低. 图12 第三部分的总分分布 (a)第一题 (b)第二题 (c) 第三题 (d)第四题 图13 第三部分各题得分分布 4.2.2 结果分析 第三部分得分率较低的原因如下: 1)第三部分主要考查乒乓球在风洞内受到的摩擦阻力及相关物理性质,属于气体流动的知识范畴,在大学物理实验教学中涉及较少,大部分学生的知识储备不足. 2)尽管赛前已经公布了使用的直流电源及示波器型号,题目中也给出了风洞的工作原理图,但大部分学生并没有正确连接实物电路,因而无法进行后续的测量. 学生遇到的主要问题是:测量频率时如何连接示波器;用多路直流电源分别给风扇和光电传感器供电时,分不清楚是2路独立的电路系统. 3)试题中已给出风速仪的插口位置,但部分学生还是在风扇端或风洞的尾端测量风速,没有仔细阅读试题资料,未抓住实验原理的关键点. 基础实验试题A总成绩分布如图14所示,基本满足高斯分布,区分度较高. 图14 基础实验试题A的总成绩分布 第7届全国大学生物理实验竞赛基础实验试题A“流体的流动”的内容丰富、知识连贯,涵盖了从流动的液体到流动的气体,从无黏性流体理论到黏性流体性质的研究. 试题中给出约3 600字的背景知识介绍,考查了学生的阅读能力和分析理解能力. 毛细管中流体的流动和风洞实验是南开大学基础物理实验中的常规实验,竞赛过程中学生遇到的问题和实验教学中存在的问题高度契合,即学生基本实验能力的培养亟需提高. 竞赛中实验器材包括矿泉水瓶、高度台、量筒、坐标纸、PVC管、计算机风扇等,风洞实验中的频率采集电路由教师和助教焊接完成,南开大学基础物理实验中心组装的“积木式”仪器,器材成本低,实验中也充分考查了学生的动手实践能力. 物理实验在科学教育中占有重要地位. 在物理实验教学中,教师应丰富实验内容,加强实验原理的深入讲解和实验内容的创新,加强对学生实践动手能力、分析理解能力的培养,才能培养出新时代需要的高质量人才.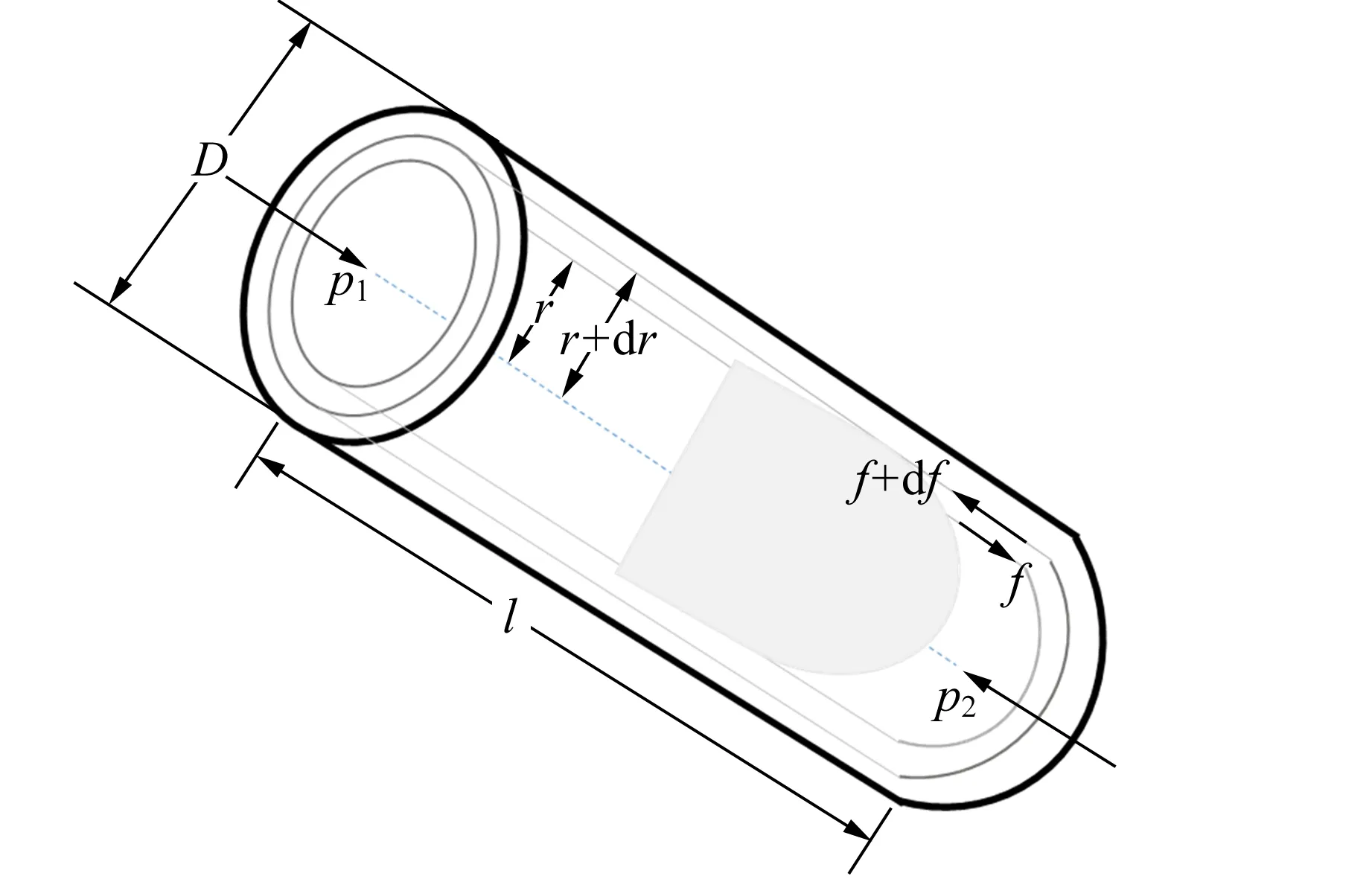
1.2 风洞
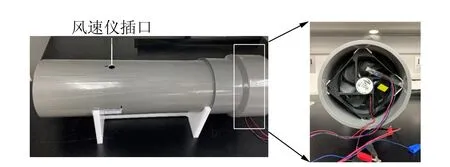
2 实验器材

3 实验任务及解答
3.1 毛细管中液体的流动


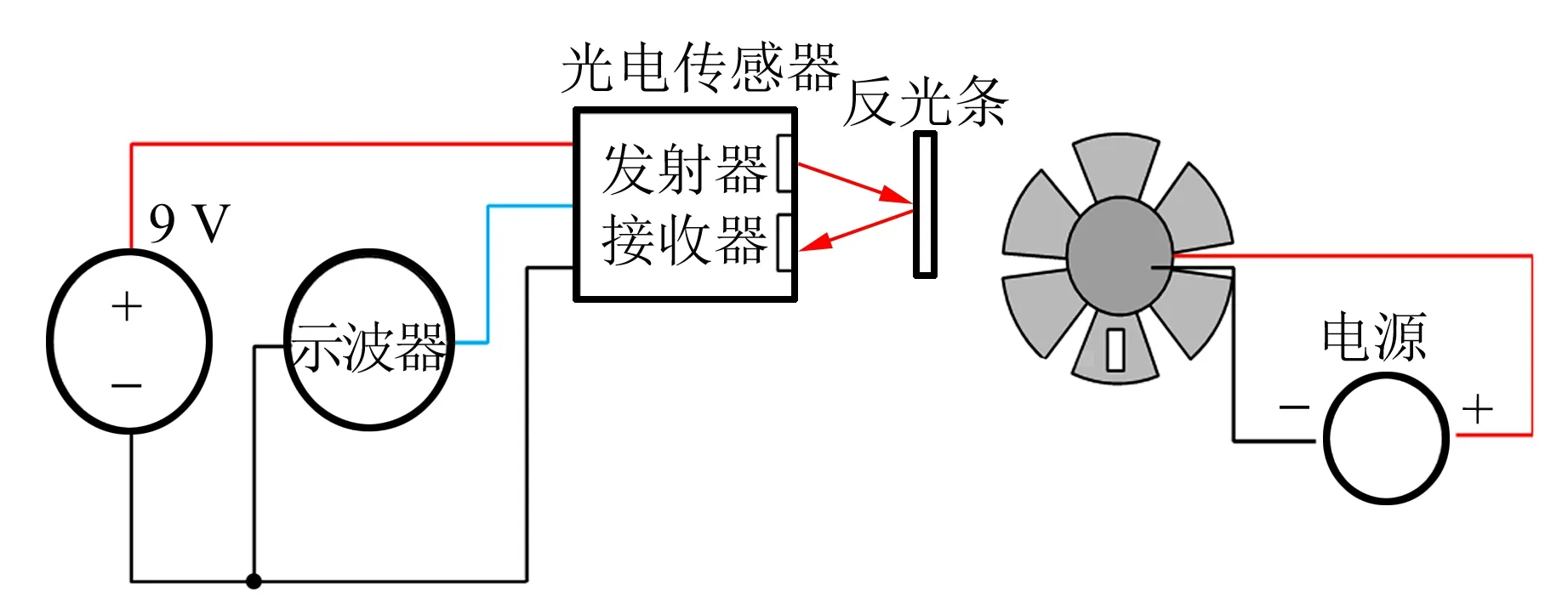
3.2 风洞




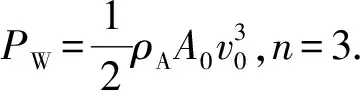
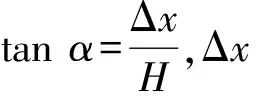
3.3 试卷附录信息
4 考试结果及评析
4.1 毛细管中液体的流动
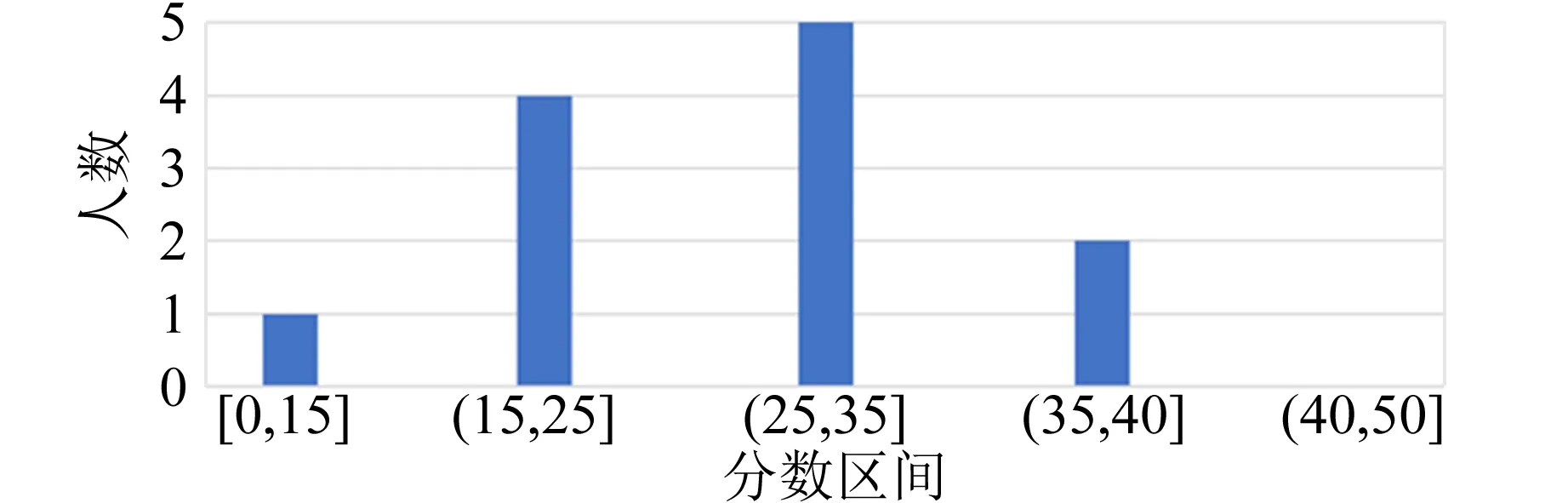
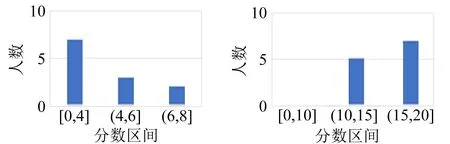
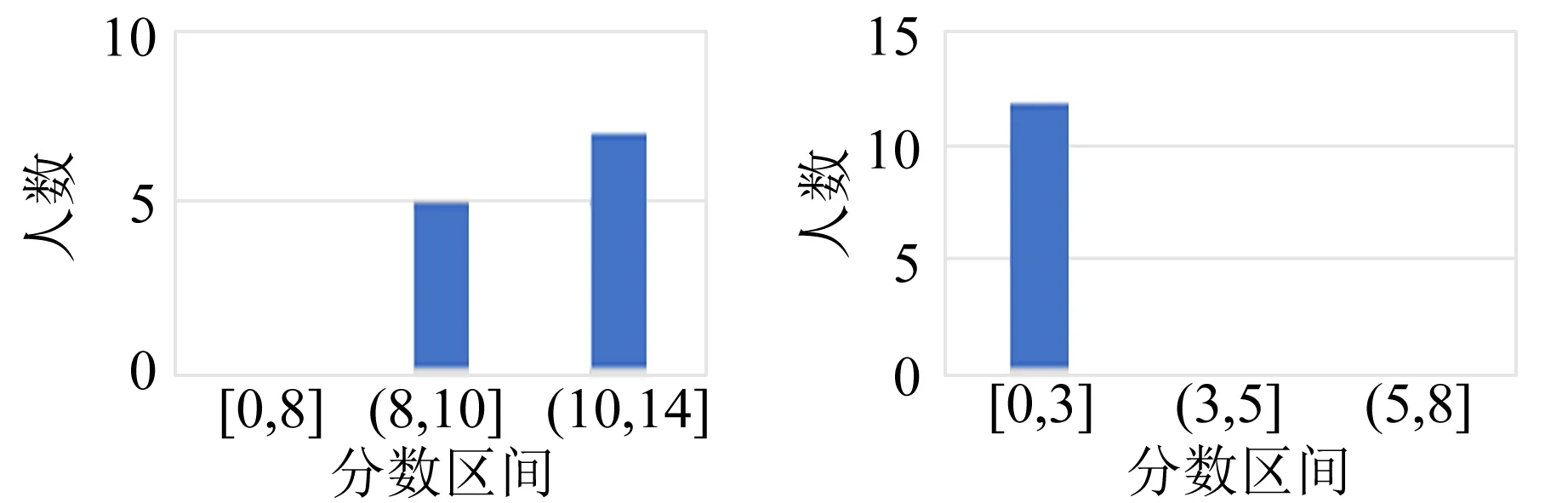
4.2 风洞
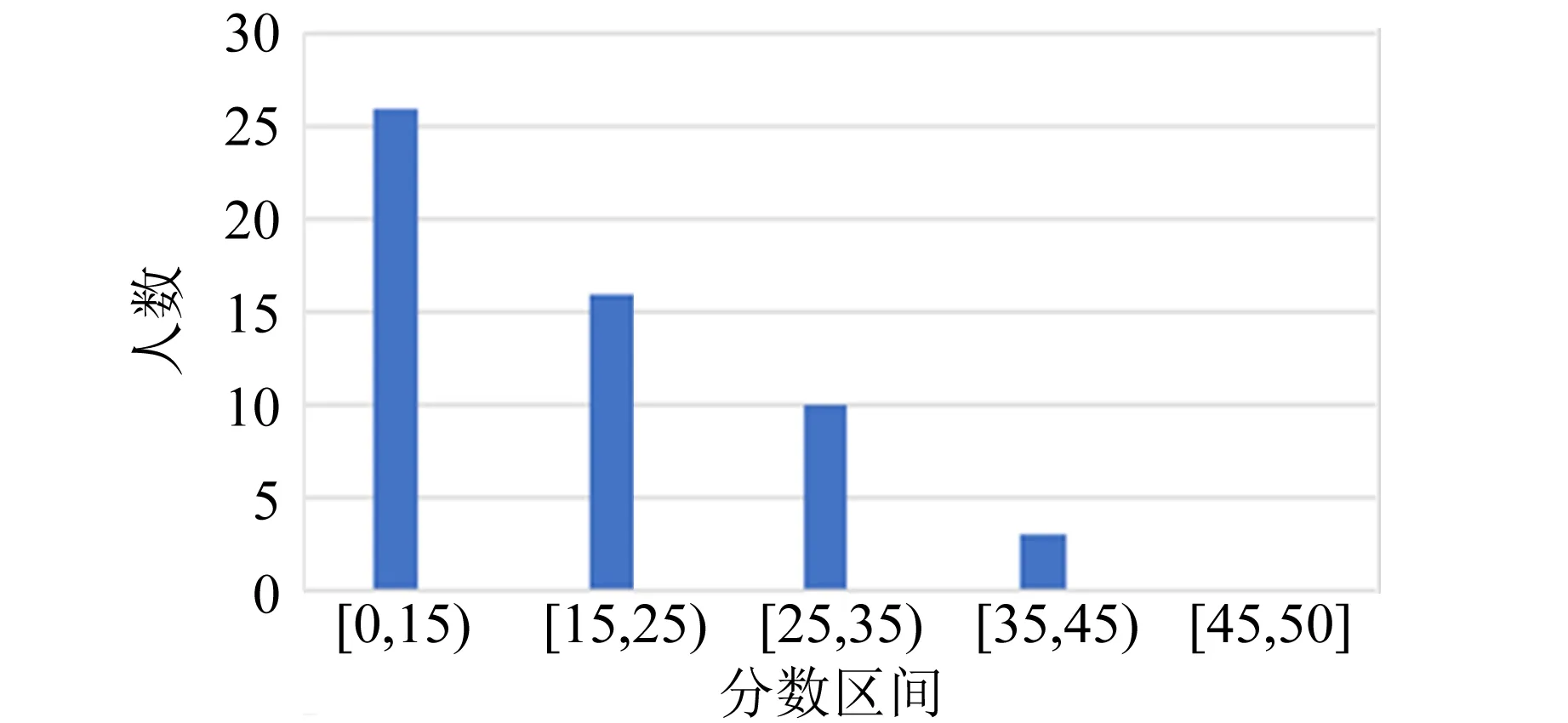
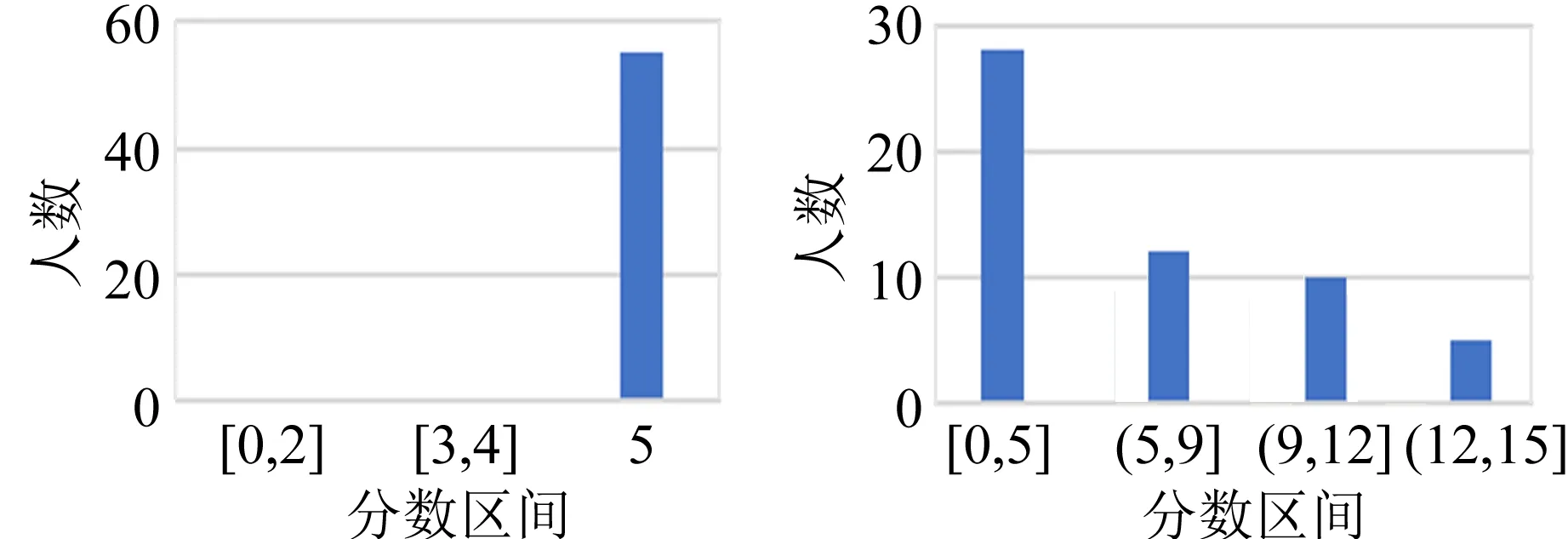
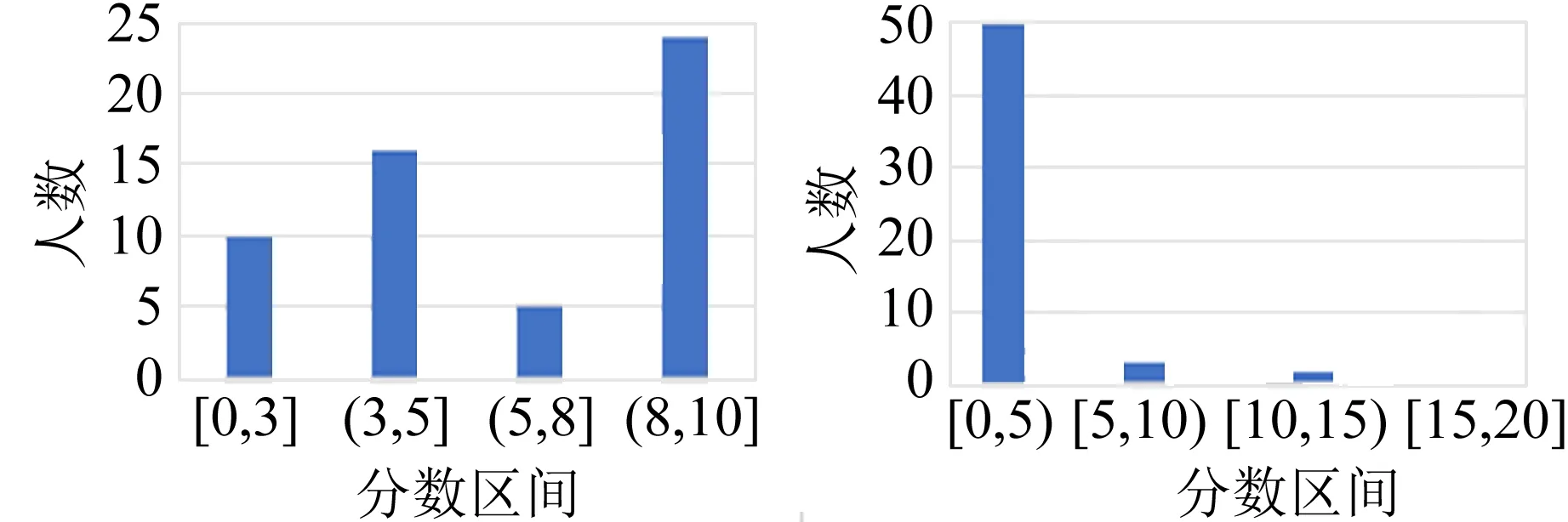
4.3 基础实验试题A总成绩分布
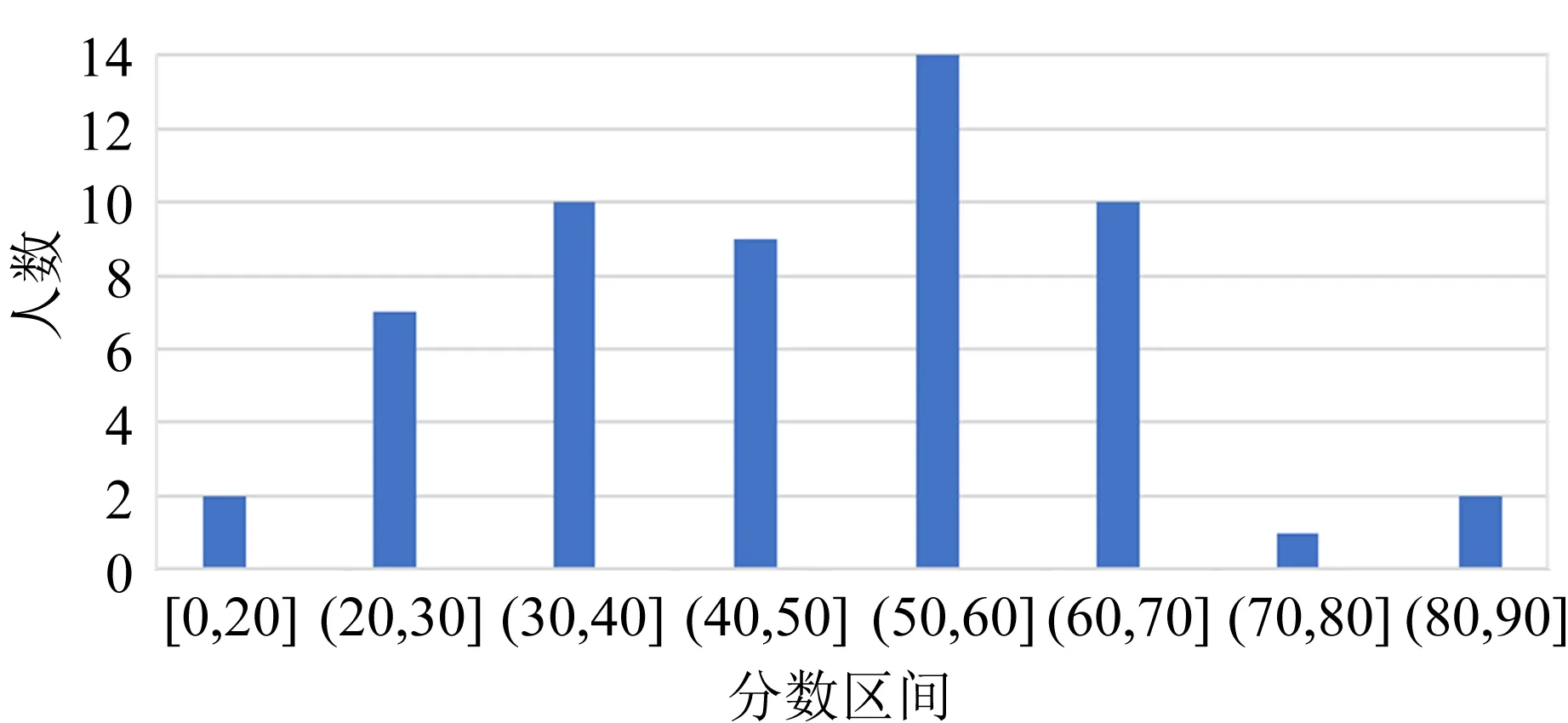
5 结束语
