基础实验试题A-1：水钟计时

王 槿，文小青，李文华,惠王伟，孔勇发

(南开大学 a.物理科学学院;b基础物理国家级实验教学示范中心，天津 300071)

在基础物理实验教学中，丰富对流体相关现象及流体参量的探究，有助于培养学生的物理思维. 第7届全国大学生物理实验竞赛(教学赛)基础实验试题A为流体的流动. 试题A分三部分：第一部分为水钟计时，第二部分为毛细管中液体的流动，第三部分为风洞，其中第一和第二部分为“二选一”形式. 基础实验试题A涉及液体的静力学及表面张力现象、动力学(液体流动及黏性)和气体动力学(空气在风洞内的流动)等相关知识. 第一部分“水钟计时”试题从流体力学的基本概念出发，考查学生对物理基本规律的认识和理解，对常用测量仪器的使用方法以及数据处理、误差分析的掌握情况，从简单生活现象发现物理问题及解决问题的能力.

1 实验原理

1.1 雷诺数与伯努利原理

流体具有流动性、黏性和压缩性. 流体的流动形态分为层流和湍流，可用雷诺数的大小来界定这2种流态. 雷诺数是流体力学中表征黏性影响的无量纲量[1]，记作Re

(1)

其中ρ，v和η分别为流体的密度、流速与黏度(动力黏度)，D为特征长度.

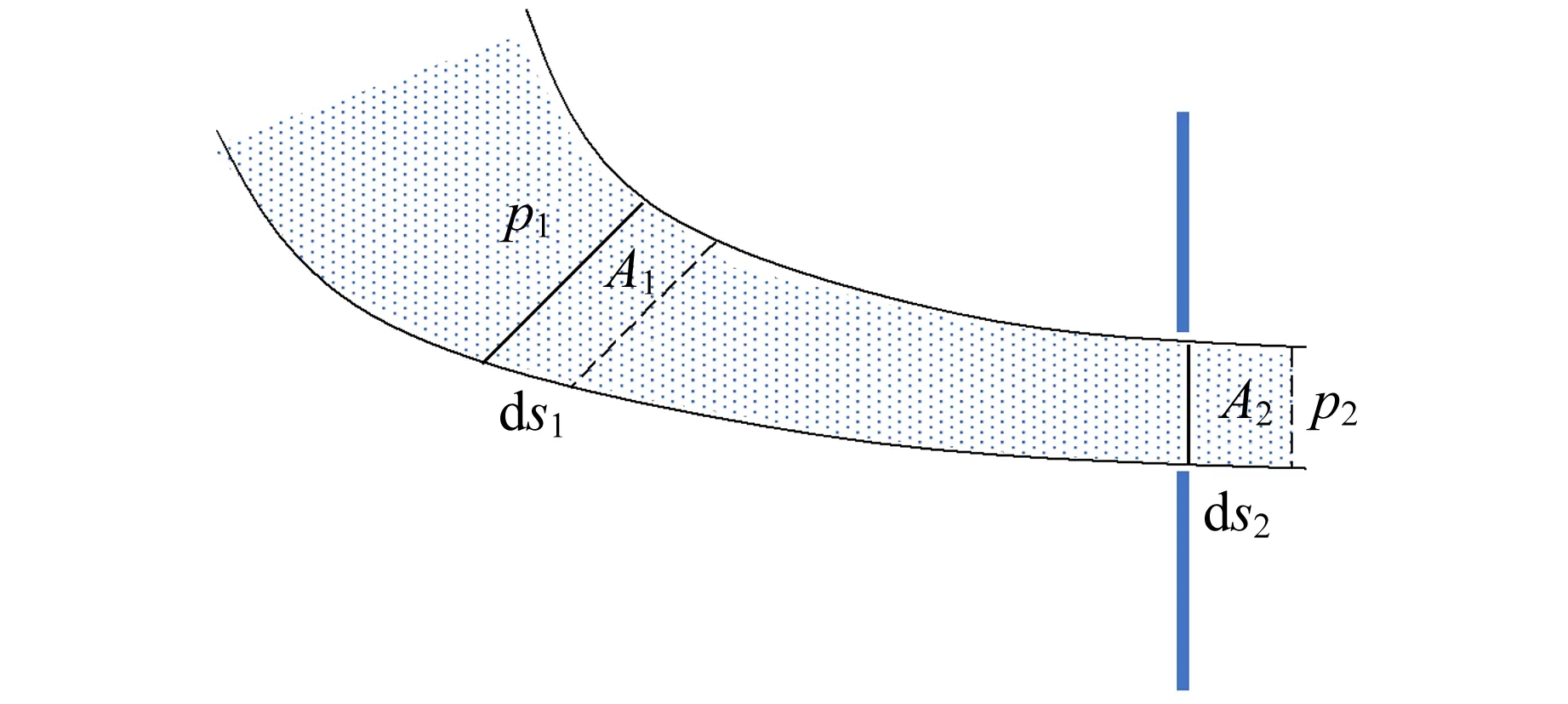
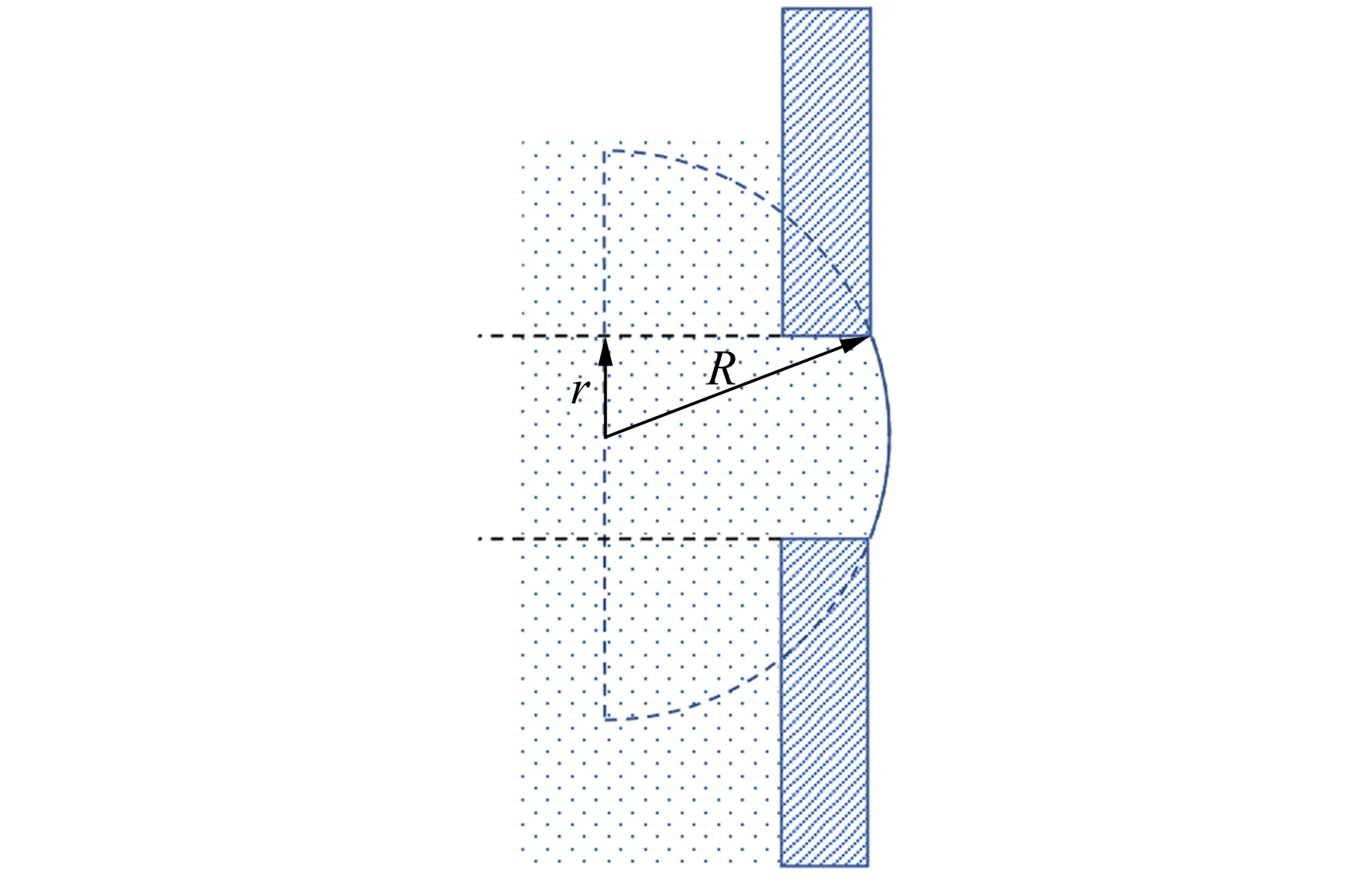
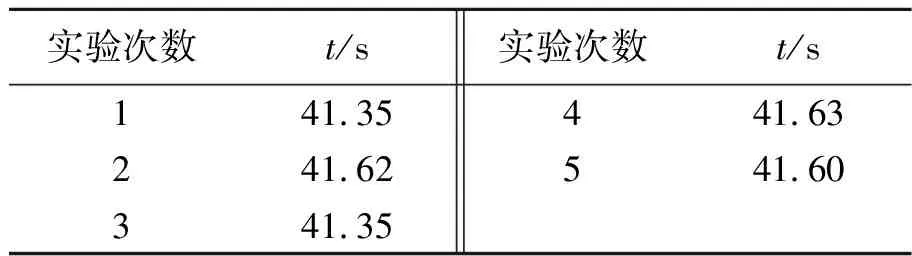
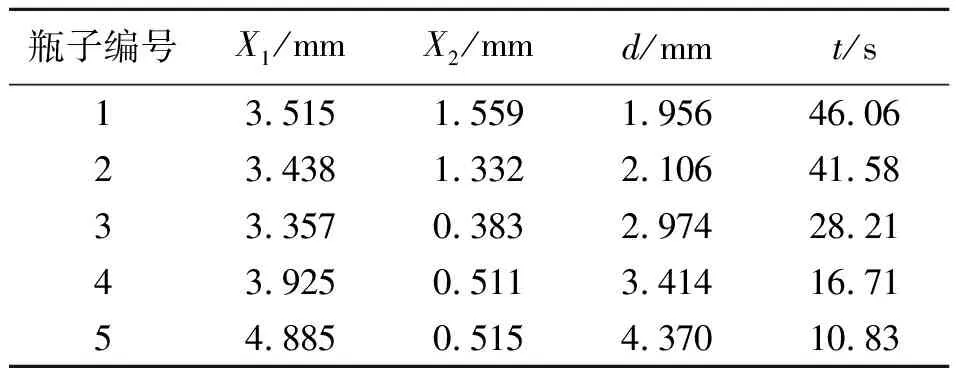
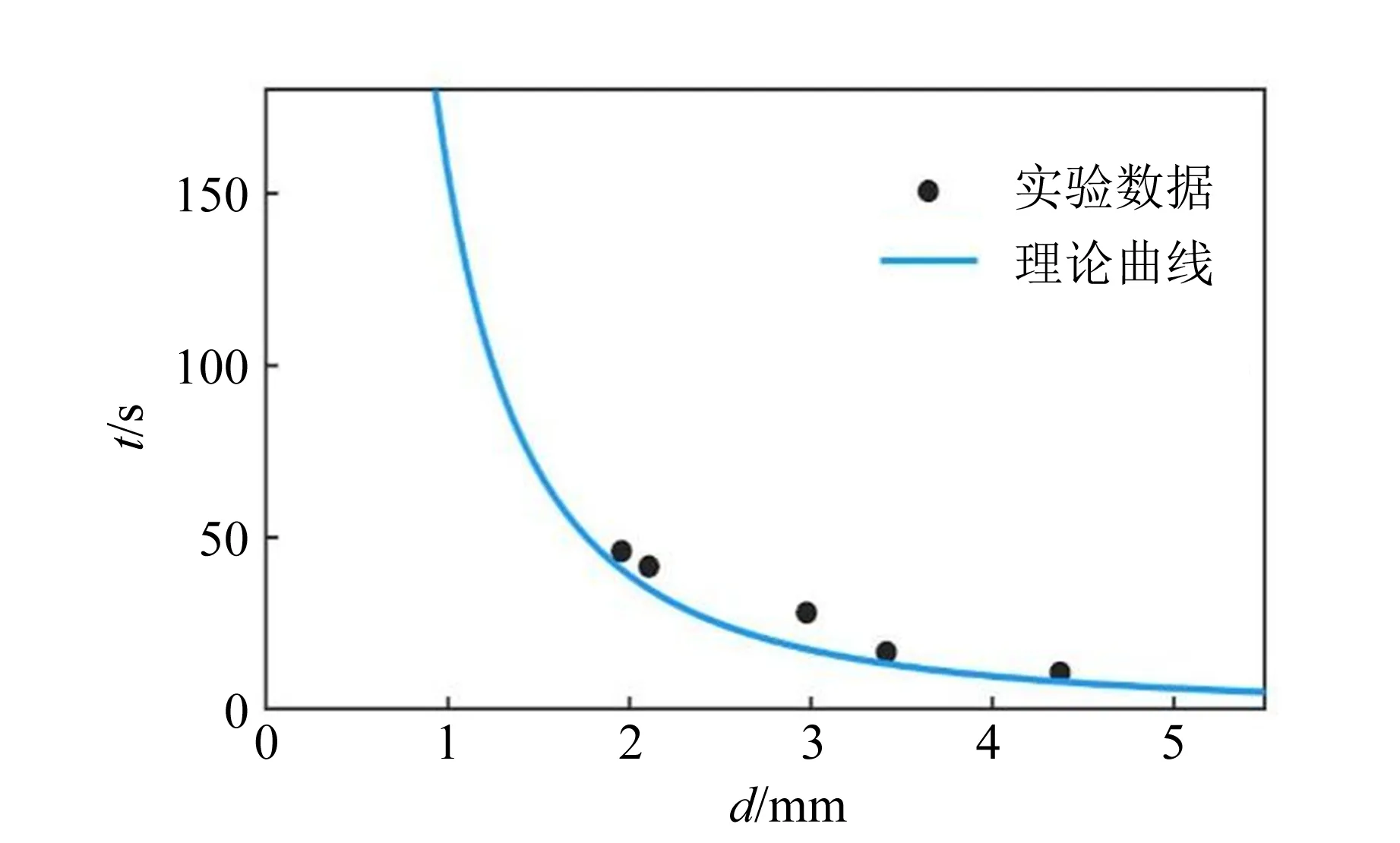
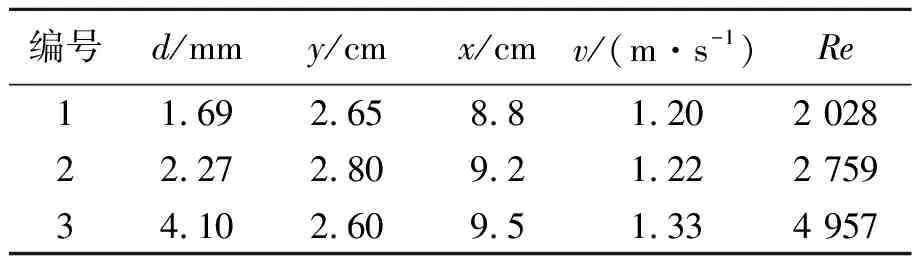
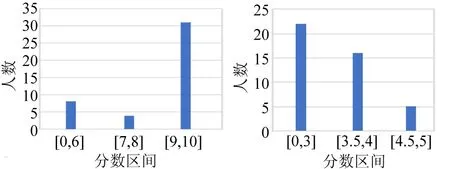
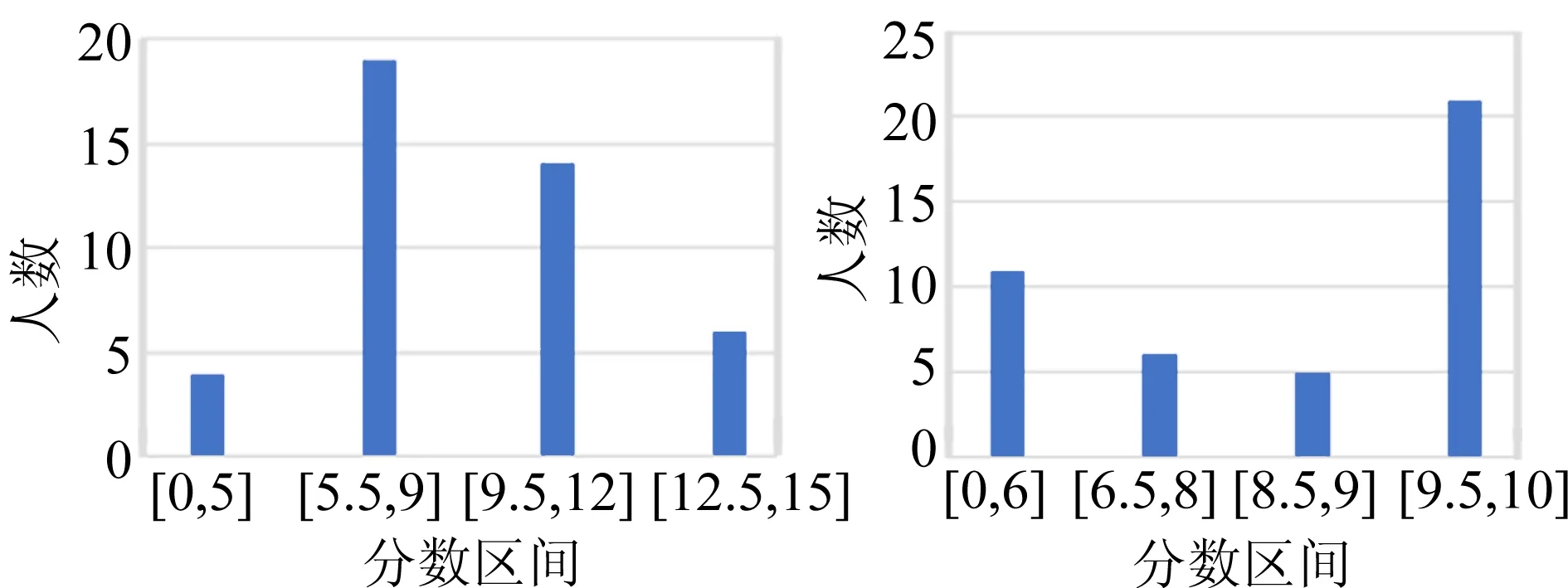
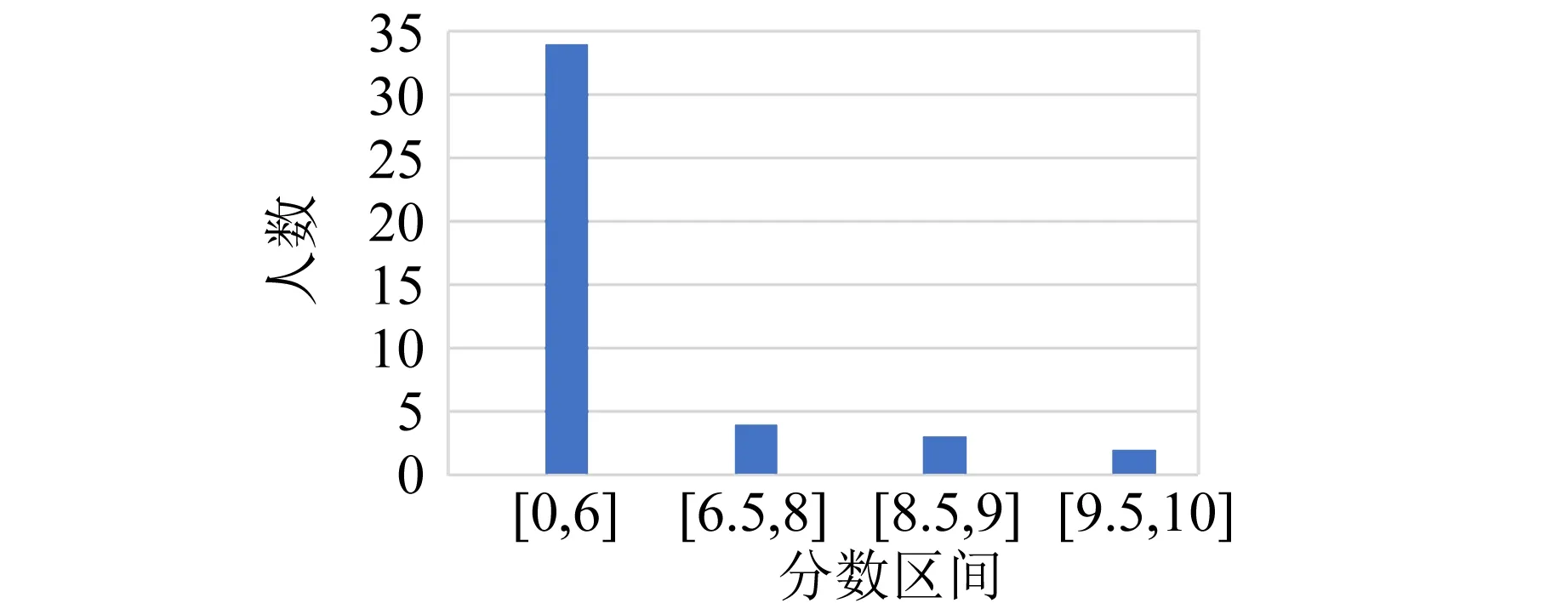
雷诺数表征流体的惯性力与黏性力之比：雷诺数较小时，黏性效应在整个流场中起主要作用，流动为层流；雷诺数较大时，惯性力占主导作用，流动逐步过渡为湍流[2].由层流过渡到湍流的雷诺数称为临界雷诺数.实验表明临界雷诺数不是固定常量，其下限约为2 000.通过改善实验条件，其上限可以提高到50 000[1].实验表明，对内壁光滑的直管而言，Re<1 000时，为层流；Re>2 000时，为湍流；当1 000

无黏性正压流体在有势外力作用下做定常流动时，通常用伯努利原理描述总能量沿流线守恒.这里考虑流体从容器侧壁开口流出的情况[2].

图1所示为某同学居家实验中研究伯努利原理的装置示意图.图2所示为伯努利原理的示意图，曲线示意流体的流线，由这2条流线所围成的区域称为流管.在流体定常、无黏、不可压缩的假设下，截面A1前进ds1距离时，截面A2前进ds2，则存在以下关系：

A1ds1=A2ds2.

(2)

图1 居家实验装置的示意图

图2 伯努利原理的示意图

如图2所示，若流管两端的压强分别为p1和p2，则流体在这一流动过程中，对流管内两截面间流体做功为

dW=p1A1ds1-p2A2ds2.

(3)

此功等于流管内流体的能量(动能和势能)的净变化量.图2所示的两处流速分别为v1和v2，高度为y1和y2，根据能量守恒和质量守恒化简得：

(4)

假设所有流线都与水的上表面垂直相交，将A1截面设置为容器中液体的上表面，A2截面设置为容器侧壁小孔，则由式(4)可得：

(5)

(6)

即托里拆利定律.

水流离开小孔后的运动可看作具有初速度v0的平抛运动，其运动方程为

(7)

其中，x和y为水流轨迹坐标，x0和y0为小孔位置坐标，消去时间t可得轨迹方程为

(8)

由式(8)可知水流轨迹为抛物线.在容器内液面高度近似不变的情况下，通过测量水流离开小孔后的轨迹位置(x,y)，根据式(8)可得到此时流体流出小孔的速度v0.

试题阅读部分给出了动能项和势能项的详细推导过程.由于篇幅限制，此处伯努利方程的推导过程做了简化.

1.2 水钟计时原理

古代计时工具有日晷、沙漏、滴漏、燃香、脉搏、水钟等，现代计时器有秒表、电磁打点计时器、数字毫秒计、摄像机、示波器、石英晶体振荡器等[4].例如，2020年国际青年物理学家锦标赛中第6题“撒克逊碗”[5-6]的研究内容也是古代计时.

对于图1所示的流体情况，当对容器中液面高度进行监测时，假设液面面积为A1，小孔面积为A0，则由式(2)可得：

(9)

联立式(6)，得到液面由距离小孔高度h1下降到h2用时为[7]

(10)

式(10)即为水钟的计时原理.

1.3 表面张力系数

液体的表面张力与液体表面相切.如果在液体表面画1条假设直线，则表面张力的作用表现为线段两端的液面存在一定的拉力，并且力的方向与线段垂直，力的大小与该线段的长度成正比[3]，即

Fα=αL,

(11)

其中，比例系数α为液体的表面张力系数，表示单位长度的线段两侧液面的相互拉力.

在观察流体流动时发现，容器中液面在下降到距离小孔一定高度h时不再下降，此时由杨-拉普拉斯公式得到：

(12)

其中，R为小孔处液体表面的曲率半径，g为重力加速度.水流停止时小孔处的液面示意图如图3所示.

图3 水流停止时小孔开口处的液面示意图

2 实验器材

第一部分的器材有：

a.贴有标号的侧壁开孔空水瓶5个；

b.塑料水槽1个；

c.高度台1个；

d.细木棍2根；

e.橡皮筋4条；

f.记号笔1支.

共用器材有：

a.移测显微镜1台；

b.量程0～100.0 ℃温度计1支；

c.秒表1块；

d.烧杯1～2个；

e.铁架台1个，夹子若干；

f.游标卡尺1把；

g.含待测液体的洗瓶2个；

h.刻度尺2把；

i.透明胶带1卷；

j.废液桶1个；

k.LED照明灯1盏；

l.抹布2块.

3 实验任务

1)根据水钟计时原理，当水瓶侧壁开孔孔径分别为1，2，3，4，5 mm时，计算液面由距孔高度h1=10 cm下降至h2=5 cm所需时间. (10分)

2)从1～3号瓶子中选择1个，重复多次实验，观察并记录液面从距离开孔高度h1=10 cm下降至h2=5 cm所需的时间，是否有明显变化？计算测量结果的A类不确定度. 记录水瓶编号(已标注在瓶身)，置信概率取P=0.683，t分布关系见附录2. (5分)

3)用提供的5个开孔大小不同的瓶子，探究液面由距孔高度h1=10 cm下降至h2=5 cm所用时间与孔径大小的关系(粗测小孔孔径，只测1次)，相关数据记录到答题纸上. 分析实验结果是否与1.1中理论计算得到的规律相符？从精度和准确度方面简要分析水瓶计时装置. (15分)

4)在液面下降实验中，水流停止流出时，容器内液面距小孔还有一定高度. 试分析该现象产生的原因. 测量此时液面距小孔高度h，试计算此时小孔处液面的曲率半径. 将其与小孔直径对比，分析两者是否在同一数量级上. 从附录中查取所需常量. (10分)

5)假设待测液体在室温下的黏度η=1.00×10-3Pa·s，任意选择1个水瓶，在液面距离小孔10 cm时，计算理论出口流速及理论雷诺数. 设计实验方案，根据平抛运动规律，测量所需要的数据，计算实际出口流速及实验雷诺数. 分析液体的流动是否满足层流条件. (10分)

试卷附录信息：

附录1：所提供的液体在不同温度下的密度.

附录2：不同置信概率时,t分布的置信系数与自由度的关系.

附录3：所提供液体在不同温度时与液相分界面的表面张力系数α.

附录4：移测显微镜使用说明(JC-10，上海光学仪器五厂).

4 试题解答

1)题设要求清晰，根据式(10)进行计算. 要求测量的水瓶直径在参考值附近，能够使用50分度游标卡尺进行测量，有效数字正确. 根据实际测量值，要求理论计算结果及表示正确. 由于制造工艺，水瓶的直径略有差别，此处给出参考答案. 水瓶直径D在60.8 mm附近，加工精度造成的直径测量偏差为0.5 mm. 不同开孔直径时液面下降时间的理论计算值如表1所示.

表1 不同开孔直径时液面下降时间的理论计算值

2)此部分内容主要考查了学生对移测显微镜的操作以及数据处理知识，包括随机误差、A类不确定度的计算.

学生根据选择和实际测量填写瓶子的编号和小孔的直径，测量工具为移测显微镜和(或者)米尺. 实验中给出的移测显微镜量程为4 mm，当孔径超过4 mm时用米尺或者游标卡尺进行测量.

如表2所示，实验测5组数据，时间基本保持不变. 孔径对应1～5 mm范围，时间在155.08～6.20 s范围.

表2 某组下降时间的实验数据

本题需要学生根据自己的测量结果正确计算出不确定度，有效数字位数正确，并得出实验结论，即时间基本保持不变，随机误差较小.

表3 某组实验的小孔直径和下降时间数据

分析结果主要包括：

a.某组实验下降时间随孔径的变化如图4所示，下降时间主要取决于孔径大小. 孔径越大，下降时间越短，与理论变化趋势相同.

b.下降时间t的实验数据普遍比理论数据大，可能是孔口不规则、黏滞作用等因素导致.

c.理论下降时间和实验下降时间差别较大，结合上一题的分析，得出结论：水瓶计时装置的精度较高，准确度较低.

图4 某组实验下降时间随孔径的变化

4)要求学生分析出该现象由表面张力产生；能够读出液面高度，记录液体温度，查表获得相应的表面张力系数值，查表获得对应的密度值. 由式(12)计算小孔处液面的曲率半径，得出结论：小孔处液面的曲率半径和小孔直径在同一数量级.

5)理论计算：将h=10 cm,g=9.8 m/s2代入式(6)，出口处理想流速v=1.4 m/s. 测量液体温度，查表得到液体密度. 例如,水温24 ℃,ρ=997.32 kg/m3,液体的黏度η=1.00×10-3Pa·s，当特征长度取管口直径D=0.002 14 m，代入式(1)得到理论雷诺数为2 998，液体不满足层流假设. 学生需要结合自己实验中选择的孔径进行计算，对是否符合层流情况做出分析.

实验测量：水流离开小孔后的运动看作平抛运动，其运动方程由式(7)给出.要求学生能够描述测量方案，测量小孔到瓶底的距离y和水平距离x.由y得到时间t，并根据测量值计算得出实际的流速和雷诺数.

表4给出了某组3个不同孔径水瓶的实验结果，水温为18 ℃，ρ=997.62 kg/m3. 将实验结果与理论分析对比，可以发现：在较大孔径下，液体均不满足层流假设；当孔径较小时，液体呈现向层流过渡的趋势.

表4 某组水瓶的出口流速及雷诺数的计算结果

5 考试结果及评析

5.1 得分分布

基础实验试题A第一部分共计5道题，总分50分. 参加考试的55名考生中有43人选择了第一部分，占比78.18%. 总分得分情况如图5所示，具体题目得分分布如图6所示.

图5 总分得分情况

(a)第一题 (b)第二题

(c)第三题 (d)第四题

(e) 第五题 图6 各题目得分情况

5.2 结果分析

基础实验试题A的阅读材料共计15页，其中与第一部分相关的背景知识约占7页. 试卷给出了大量关于伯努利方程的阅读内容，可应用于第五题中的实验设计. 大部分考查的内容是基本仪器和数据处理相关知识，例如精度与准确度分析，误差与不确定度评定，误差的来源与分类. 试卷结果显示部分考生对基本的测量常识掌握得不够准确，存在概念混淆，例如精度与准确度.

在仪器的使用方面，大部分考生会使用移测显微镜，但是部分考生测量时没有使用光源，可能导致读数不准确. 实验中需要固定圆瓶，考生利用木棍、橡皮筋、胶带和高度台，在较短时间内给出了不同的固定方案.

水钟计时实验是南开大学基础物理实验中的常规实验，在2020年春季疫情期间开始进行该内容的线上教学，后期拓展为课堂实践. 实验器材包括矿泉水瓶、高度台和摄影支架，实验成本较低. 实验教学内容比本次竞赛考核内容丰富，课上学生使用手机进行摄像录制，使用Tracker提取液面，开展托里拆利定律的验证和理论模型的修正等内容. 此实验的拓展研究包括对黏滞和表面张力影响的进一步讨论. 由于实验竞赛现场并没有配备电脑，不具备实时液面下降高度数据采集和数据拟合的功能，并未进一步考查能量耗散情况下托里拆利定律的修正. 这部分内容可以参考文献[8-9].