考虑磨损的组合密封性能分析

王军润， 闫晓亮， 常 凯

(航空工业庆安集团有限公司航空设备研究所， 陕西 西安 710077)

引言

在飞机液压系统中，组合密封为一种常见的外部动密封形式，常应用于飞机作动系统的执行机构中。工作过程中密封圈在预压缩和油压的双重作用下，接触表面不可避免地存在磨损现象，随着密封圈材料的不断损失会引起密封效果下降、泄漏量增大，严重的泄漏会导致系统功能失效甚至会威胁飞行安全。因此，对密封圈磨损过程和基于密封圈磨损的使用寿命预测方法研究具有重要的实际意义。

目前对于密封材料磨损的研究多采用试验的方法，其中销-盘试验为常用的试验方法。但是即使对于同一种材料，在不同工况下的边界条件和初始工况也会存在显著区别，因此仅靠销-盘试验无法在设计阶段预测密封寿命。采用全尺寸实物试验可以模拟真实的使用工况，并对密封圈的磨损进行精确预测，但这样非常耗时耗力。

磨损的数值模拟可以克服上述缺点而逐渐替代物理试验，而且在可靠的磨损试验数据支撑下可以进行参数化研究。一些学者研究了密封圈磨损的数值仿真方法，其中有限元法应用最为广泛。PODRA P等[1]采用有限元软件模拟了金属和陶瓷之间的磨损行为。SODERBERG A[2]研究了钢在粗糙表面滑过时表面材料的损失过程。王正磊等[3-5]研究了轴向柱塞泵配流副的摩擦磨损特性及使用性能的关系。GODA T等[6]采用有限元模型模拟了高分子材料的摩擦和磨损行为。但上述研究多集中在硬材料上，只模拟了表面单元层的材料损失，对于如橡胶、塑料等软材料，需要模拟更大的体积损失才能有效预测密封圈的寿命。近年来，一些学者采用一种相对稳定的不需改变ANSYS网格单元数的方法来模拟软材料结构的磨损过程，如LI X等[7-9]。

本研究针对由橡胶弹性体和塑料滑环组合而成的橡塑组合密封圈的磨损和密封性能分析方法进行研究，基于密封材料摩擦磨损试验对模型参数进行修正，并通过密封台架试验对仿真模型进行验证。

1 研究对象及数值仿真模型

1.1 研究对象

橡塑组合密封圈一般由橡胶圈和塑料滑环组合而成，多应用于动密封场合。橡胶圈提供弹性预紧力，塑料滑环与运动的轴直接接触，形成主要工作面。格莱圈为一种可应用于旋转动密封场合的橡塑组合密封圈，其密封系统示意图如图1所示。

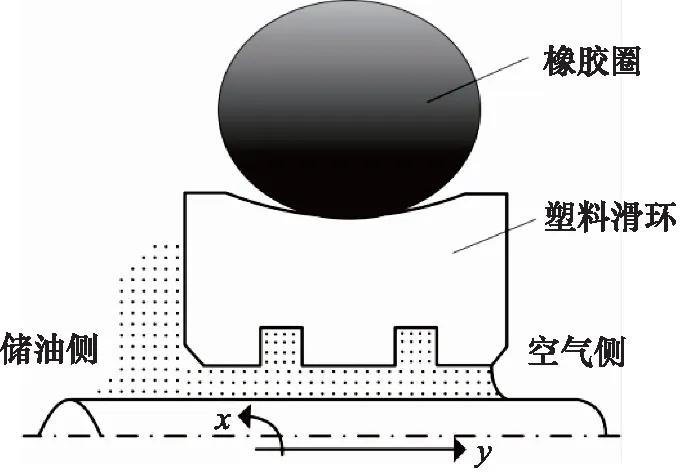
图1 旋转密封结构示意图Fig.1 Structural sketch of rotary seal

组合密封圈的滑环由具有较低摩擦系数的改性聚四氟乙烯材料制成，且滑环可以做的较薄，在发生磨损后依靠橡胶圈提供的弹力可与轴保持较好的贴合，维持密封能力。

1.2 固体力学求解模型

旋转格莱圈包含橡胶材料和塑料材料，橡胶材料为超弹性材料，可以用超弹性本构模型通过应变能密度函数来定义。本研究用Mooney-Rivlin模型来定义其本构模型，其表达式如下：

w=C10(I1-3)+C01(I2-3)

(1)

式中，w—— 应变能密度

C10,C01—— 橡胶材料常数

I1,I2—— 分别为第1，第2 Green应变不变量

针对所使用的某航空橡胶材料，通过力学试验测得其材料常数为C10=1.92，C01=0.58。

旋转格莱圈的滑环使用改性聚四氟乙烯(PTFE)塑料，由于密封圈在使用过程中处于小变形状态，塑料材料可认为处于小变形、线弹性接触状态，因此采用Boussinesq提出的积分式来进行表面弹性变形的近似求解，其二维表达式如下：

(2)

式中，p—— 流体或固体接触压力

E′ —— 等效弹性模量

在数值求解时，一般可将上式离散成如下形式[10]：

(3)

式中，Dk为相关系数，根据所取的无量纲参数来确定；Di,j为有量纲影响系数。

1.3 流体力学求解模型

密封圈在工作状态下，会在密封区域形成稳定的油膜。因油膜厚度远小于轴的曲率半径，可忽略轴曲率的影响，建立描述流体特性的二维Reynolds方程如下所示：

(4)

式中，ρ—— 油液密度

h—— 油膜厚度

p—— 流体压力

η—— 油液黏度

ue—— 2个表面运动速度的平均值

边界条件采用雷诺边界条件，具体如下：

(5)

式中,ps—— 密封压力

pa—— 大气压力

yin—— 油压侧边界坐标

yout—— 大气侧边界坐标

如果密封间隙中充满油液，轴在旋转时将产生流体动压润滑油膜，此时密封接触面任意点间的间隙为：

h(x,y)=havg+zseal(x,y)+zshaft(x,y)+ν(x,y)

(6)

式中，havg—— 中心油膜厚度

zseal—— 密封唇表面粗糙度

zshaft—— 轴表面粗糙度

ν—— 油膜压力下密封唇表面弹性变形量

表面弹性变形由Boussinesq积分表达式得到。油液的黏度采用Roelands黏-压关系式：

η=η0exp{(lnη0+9.67)[(1+5.1×10-9p)z0-1]}

(7)

式中，α—— 黏-压系数

η0—— 润滑油的环境黏度

式(7)中,无量纲常数z0的表达式为：

(8)

润滑油的密度采用Dowson-Higginson密-压公式来计算：

(9)

式中，ρ0—— 润滑油的环境密度

1.4 磨损仿真分析模型

磨损速率的通用表达式为[11]：

(10)

式中，h—— 磨损高度

k—— 无量纲磨损速率

p—— 接触压力

u—— 相对滑动速度

H—— 运动副中较软材料的硬度

α，β，γ—— 与采用的磨损理论有关

Archard磨损模型对黏着磨损、磨粒磨损和疲劳磨损等形式具有通用性，只是式中的磨损系数的意义不同。当采用Archard磨损模型时，上式中α=β=γ=1。

定义Kh=K/H为材料的磨损速率，则式(7)可写成：

dh=Kh×p×dL

(11)

一般情况下，接触压力p是随时间变化的，式(11)可写成：

dh=Kh×p(t)×u×dt

(12)

式(12)即为密封圈磨损仿真分析的数学模型。

2 仿真的实现方法

2.1 仿真求解流程

考虑密封圈材料磨损的动密封性能仿真分析时，需进行磨损仿真分析和流体力学仿真分析，磨损仿真分析用于模拟特定润滑状态下密封圈材料的磨损过程，流体力学仿真分析用于模拟密封圈磨损后的润滑性能。两个仿真分析依次迭代求解，每完成一轮迭代后判断是否满足收敛条件。其中，磨损仿真分析中包括节点的磨损高度计算、磨损后的密封圈结构建模和新的接触压力求解；流体力学仿真分析包括油膜压力的迭代求解和油膜厚度的迭代求解，仿真求解流图如图2所示。

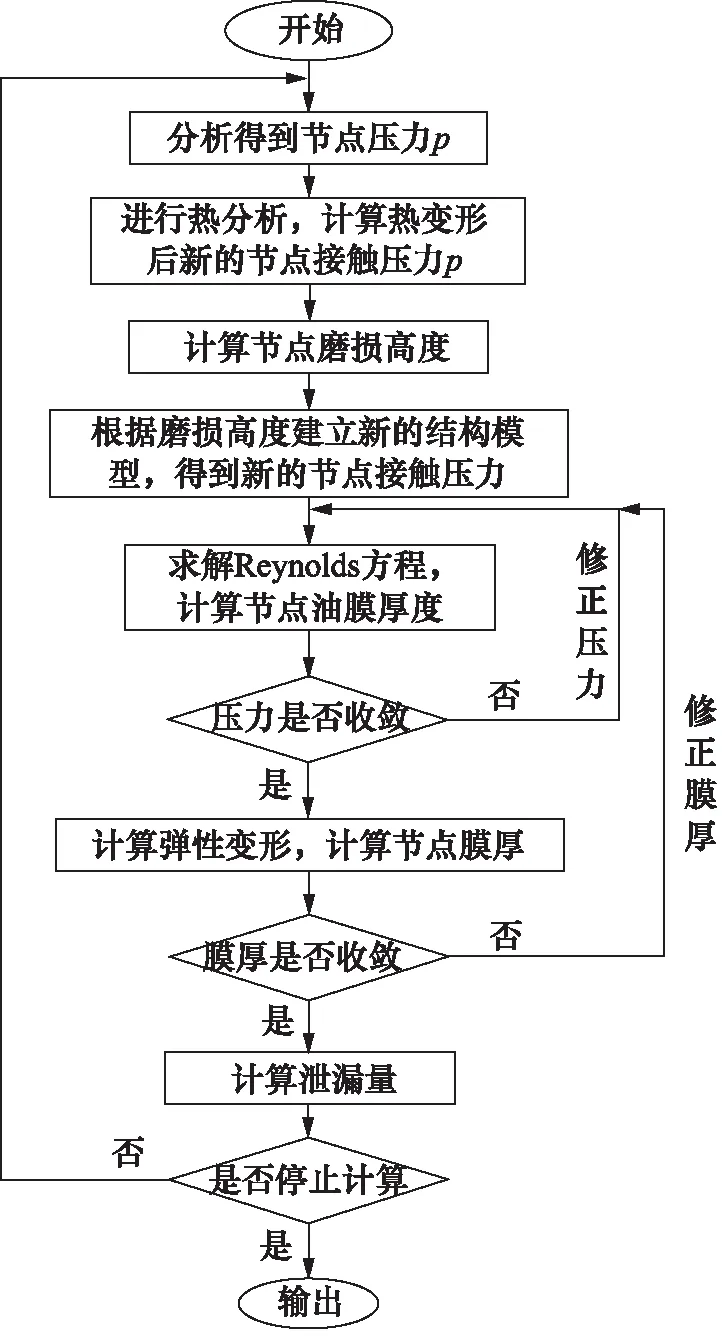
图2 仿真求解流程Fig.2 Simulation solution flow

在流体力学数值求解时，采用有限差分法对Reynolds方程进行求解，其中对Reynolds方程的左端项采用中心差分，对右端项采用向后差分，压力和膜厚的收敛准则为相对误差小于1.0×10-5。

2.2 接触压力求解

在密封圈磨损的仿真分析过程中，接触压力随着材料的逐渐磨损而不断变化。现有的商用有限元软件可以对密封圈的接触压力进行求解，但无法模拟材料的损失过程，所以需要找到一种模拟密封圈材料不断损失的仿真方法。BÉKÉSI N等[12]提出了一种针对材料磨损的全局网格重构法，但该方法在尖角处存在网格重划分困难的缺点。有些学者采用“杀死单元法”，即当某个单元上的接触压力超过压力极限时，将该单元“杀死”。这种方法也存在一定的局限性，即在磨损的模拟过程中材料的损失是以单元为最小单位，无法对微小的磨损量进行模拟，而且“杀死”单元极易造成网格边缘出现尖角、尖边等异常情况，导致不收敛。LI X等[7]提出了一种不改变网格数量，只调整参与磨损的单元和单元尺寸的新方法。采用该方法需要特别注意单元尺寸调整方法的选择，否则也容易导致网格畸形。

本研究采用有限元软件ANSYS进行接触压力求解和磨损仿真分析，对磨损后的密封圈采用LI X等[7]提出的模型重构方法解决了磨损仿真不易收敛的问题。

2.3 摩擦热的处理

当轴高速旋转时，由于密封圈摩擦发热引起密封圈的膨胀变形进而导致磨损的现象不可忽略，因此需在磨损仿真过程中考虑摩擦热的影响。

在计算时考虑到轴的体积比密封接触区域的体积要大很多，且金属的热传导系数要显著大于橡胶和塑料，因此忽略轴的热膨胀变形，只考虑密封圈的热变形。

2.4 仿真终止条件

对于O形橡胶圈，有国家标准和行业标准中规定的最小压缩率作为判断密封性能是否有效的依据，而对于由橡胶圈和塑料滑环组合而成的组合密封圈，则没有相关的评判标准。

本研究中将密封圈磨损后的泄漏量预测结果作为评价组合密封圈是否有效的评价指标。当泄漏量预测结果大于设定的最小泄漏量时，中止计算，输出结果。

3 模型参数的获取

在磨损仿真分析时，摩擦系数和材料磨损率的准确选择至关重要。采用SRV-4高温摩擦磨损试验机，由填充玻璃纤维改性聚四氟乙烯塑料棒和表面镀硬铬的不锈钢盘，以销盘式线接触方式开展往复摩擦磨损试验；润滑介质采用15号军用航空液压油，试验件接触和运动方式如图3所示，磨损仿真分析时所选用的主要材料参数和物理参数如表1所示。

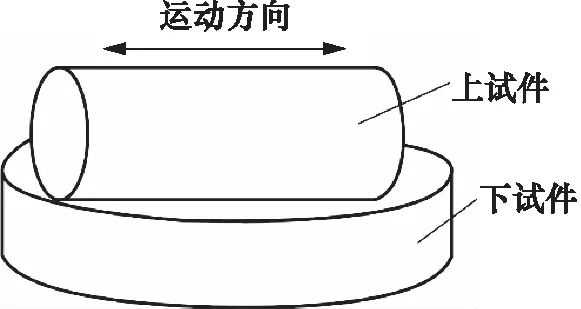
图3 试验件的接触和运动方式Fig.3 Contact and movement mode of test piece

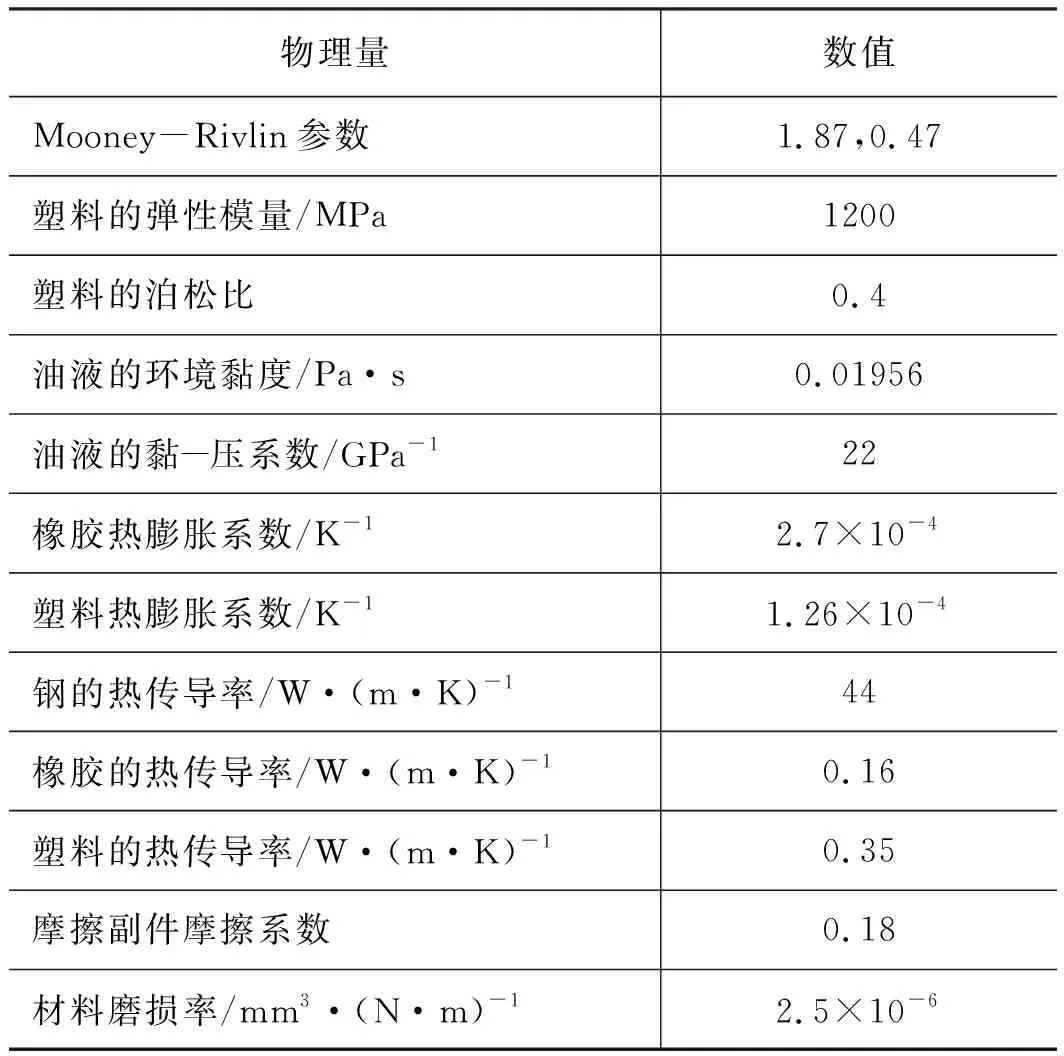
表1 材料和物理参数Tab.1 Material and physical parameters

使用电子天平测量试验前后试验件质量的变化，通过式(16)计算磨损率Kh：

(16)

式中，ρ为塑料材料的密度。

4 仿真结果与试验结果分析

4.1 仿真结果分析

下面以某旋转作动器的轴用旋转格莱圈为研究对象，对其密封性能和磨损过程进行数值模拟分析。该旋转格莱圈的内径为64.5 mm，外径为80 mm，宽度为6.3 mm。

旋转格莱圈的工作油压为21 MPa，工作时轴的表面稳定旋转速度为0.2 m/s，其有限元模型如图4所示。

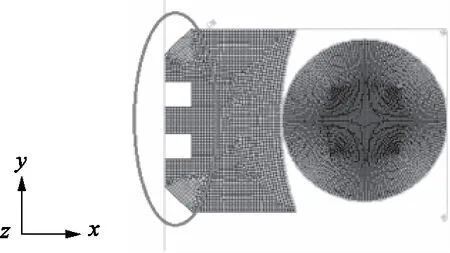
图4 旋转格莱圈的有限元模型Fig.4 Finite element model of rotating seal ring

图5所示为格莱圈没有发生磨损时，由有限元软件求解得到的干接触压力分布情况，以及由流体力学分析得到的密封间隙的油膜厚度在y-o-z平面的分布情况。从图5可以看出，由于旋转格莱圈在圆周方向开有两道矩形沟槽，因此接触压力分布不连续，在沟槽部位压力为零。而且由于沟槽的存在，使得接触区的压力梯度变得很大。

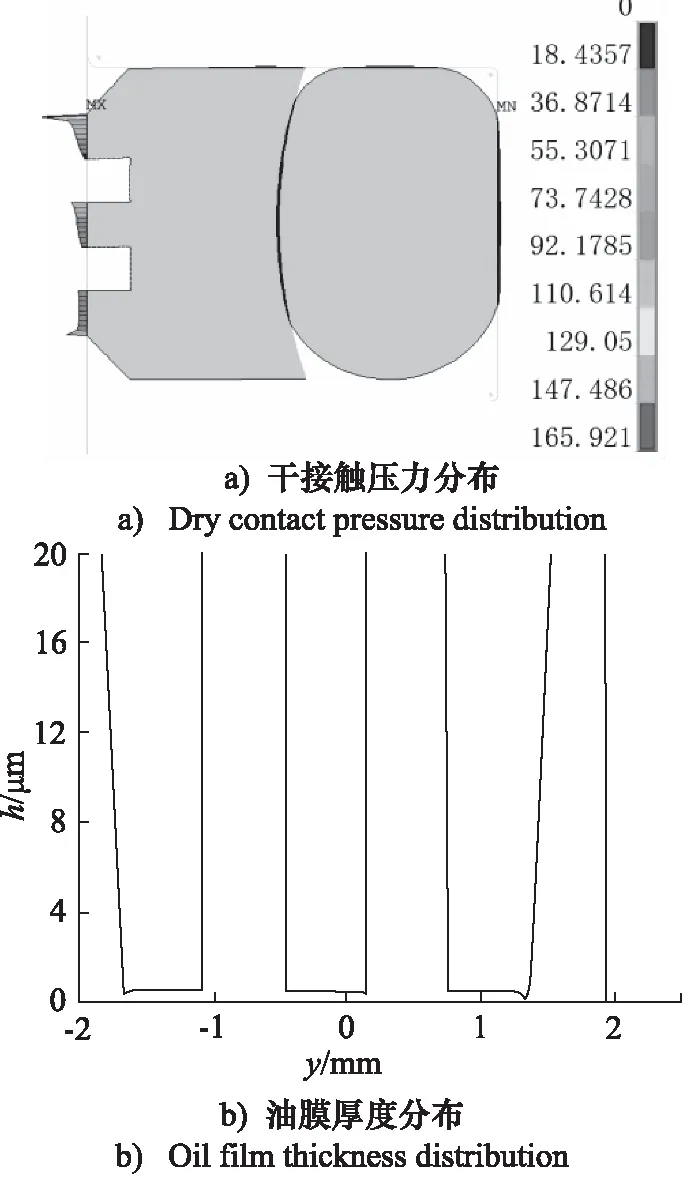
图5 格莱圈初始状态的压力和油膜厚度分布Fig.5 Pressure and oil film thickness distribution of seal ring in initial state

图6所示为密封圈表面相对运动距离为100 m，经过磨损后求解得到的干接触压力分布情况，以及密封间隙的油膜厚度在y-o-z平面的分布情况。

比较图5和图6中压力分布情况可以看出，磨损前后格莱圈的干接触压力差别较大。磨损后，格莱圈的干接触最高压力明显减小，密封圈不同部位压力承载更加均匀。从油膜厚度分布来看，密封圈未发生磨损时的油膜厚度比较平坦，这与密封圈的几何结构有关。而运动100 m经历磨损后，密封间隙的最小油膜厚度增大，密封间隙的油膜厚度波动比较剧烈。

图6 格莱圈磨损后的压力和油膜厚度分布Fig.6 Distribution of pressure and oil film thickness after seal ring wear

4.2 试验条件

为了考察旋转动密封性能、验证仿真分析模型，搭建了动密封性能试验台，试验台原理如图7所示。该试验台由液压系统、机械系统和控制系统组成，转速范围为0～9600 r/min，压力范围为0～5 MPa，油液温度最高+150 ℃，工作介质为Shell RF555润滑油。

图7 试验设备原理图Fig.7 Schematic diagram of test equipment

最终搭建的试验台如图8所示，该试验台具有旋转动密封和往复动密封试验功能，油液压力、油液温度、转速和扭矩通过传感器自动测量和记录，试验台通过自动控制水冷散热器的开合来实现温度的自动控制，泄漏量由量杯进行收集和计量。

图8 动密封试验设备实物图Fig.8 Test equipment of dynamic sealing

旋转密封试验所选取的转轴直径为φ80.0 mm，密封圈安装于转轴的槽中，外径为φ80.1 mm。密封圈为橡胶O形圈与改性聚四氟乙烯材质的矩形截面滑环组成的同轴密封圈。为了增加润滑性能减小摩擦，滑环的外圆表面开有两道油槽，如图9所示。

图9 外表面开槽的密封环实物图Fig.9 Sealing ring with slotted on outer surface

试验前，测量并记录在不同转速下不安装密封圈时的转矩，经测试不同转速下的转矩在1.1～1.3 N·m范围内。密封件及试验台安装调试完成后，先在200 r/min 转速下对密封圈进行约20 min的磨合运转，待转速和扭矩等参数稳定后开始试验。分别在0.42 MPa和1.8 MPa油压，油液温度为常温、80 ℃和110 ℃，不同转速下开展了动密封性能试验，并开展了耐久性试验。

4.3 仿真结果与试验结果对比分析

图10所示为常温(23 ℃)工况下，油压分别为0.42 MPa和1.8 MPa，不同转速n对应的密封圈扭矩T测量值与理论值的比较。从图10可以看出，密封圈的摩擦扭矩随着转速增大而呈现近似单调增大的趋势。1.8 MPa油压对应的摩擦扭矩明显大于0.42 MPa油压对应的摩擦扭矩。

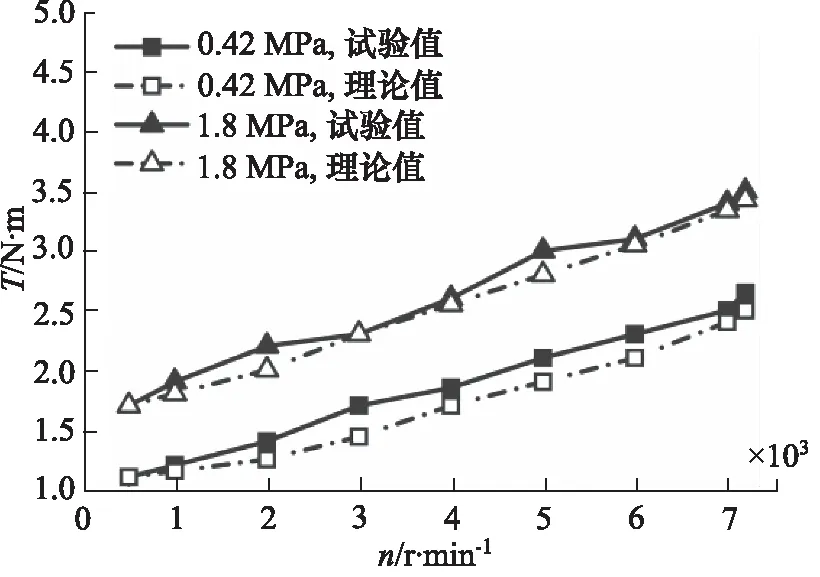
图10 常温下扭矩值对比Fig.10 Comparison of torque values at room temperature

图11所示为油液温度为110 ℃，在0.42 MPa和1.8 MPa油压下，不同转速下密封圈的扭矩测量值与理论值的比较。可以看出110 ℃高温时密封圈的摩擦扭矩与常温时的变化趋势一致，不同的是110 ℃高温时对应的摩擦扭矩要明显大于常温时的扭矩。

图11 高温110 ℃时扭矩值对比Fig.11 Comparison of torque values at 110 ℃

图12所示为常温下，油液压力为0.42 MPa和1.8 MPa，不同转速下密封圈的泄漏量Q实测值与理论值的比较。从图12可以看出，油液压力对泄漏量的影响较为明显，1.8 MPa油压对应的泄漏量要明显大于0.42 MPa油压下的泄漏量。从试验测量结果看，泄漏量会存在一定的波动，但是总体趋势是，泄漏量会随着转速的增大而增大，在低压时转速的影响更加明显。

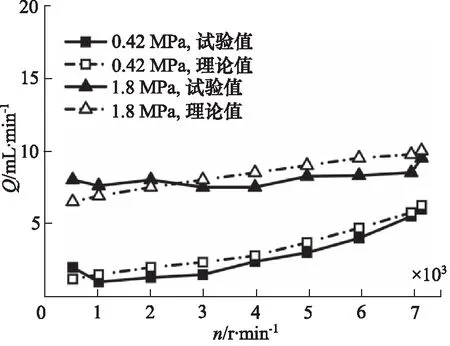
图12 常温下泄漏量的对比Fig.12 Comparison of leakage at room temperature

图13所示为油液温度110 ℃，油液压力为0.42 MPa 和1.8 MPa，不同转速下密封圈的泄漏量实测值与理论值的比较。

比较图12和图13可以看出，常温下，密封圈的泄漏量要明显高于110 ℃高温工况下，这主要是由于密封圈在高温下体积膨胀引起的。相比于常温工况，在高温时转速变化对泄漏量的影响作用减弱。

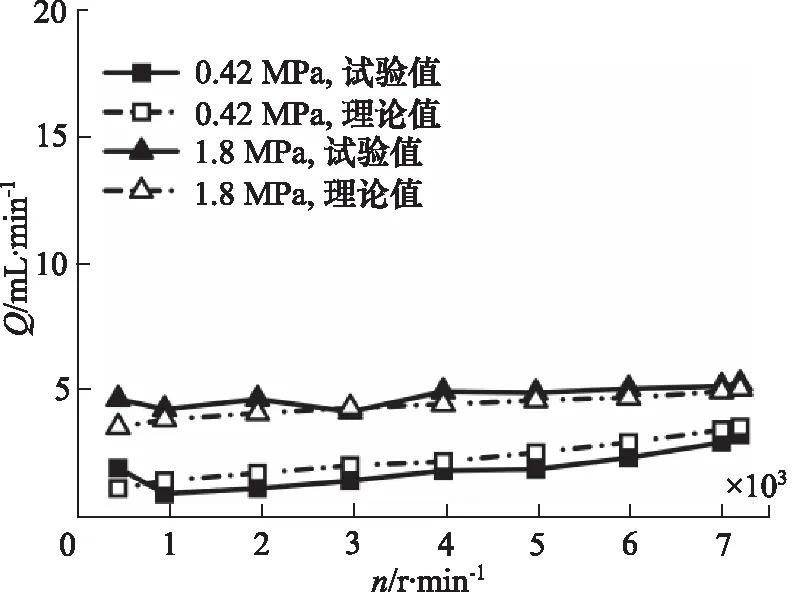
图13 高温110 ℃时泄漏量的对比Fig.13 Comparison of leakage at 110 ℃

图14所示为油液温度110 ℃、轴转速为6000 r/min工况下，油液压力分别为0.42 MPa和1.8 MPa，对密封圈开展耐久性试验的扭矩实测值与理论值的比较。在0.42 MPa油压下，当试验进行至约18.3 h，陆续出现异常响声、黑色粉末状物质随油液流出、冒烟、力矩和泄漏量突然增大现象。将试验装置拆解后，发现一侧的密封圈直径已经明显小于轴直径，如图15所示，说明密封已失效。在1.8 MPa油压下，当试验进行至约17 h，出现类似的失效现象，遂停止试验。

图14 扭矩随着时间的变化Fig.14 Torque change of different time

图15 失效后的密封件Fig.15 Failed sealing ring

图16所示为油液温度110 ℃，轴转速为6000 r/min工况下，开展耐久性试验的密封圈泄漏量的理论值和试验测量值随着时间的变化。

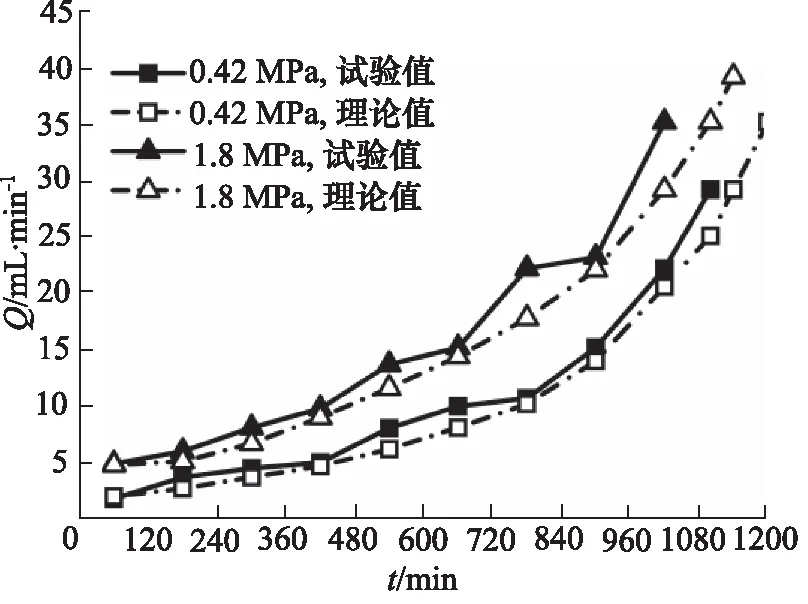
图16 泄漏量随着时间的变化Fig.16 Change of leakage with time

表2所示为不同试验工况下，密封圈的扭矩和泄漏量的试验结果和仿真分析结果的误差。从表2可以看出， 摩擦扭矩的误差相对较小， 平均误差都在10%以下，而泄漏量的误差相对较大。在0.42 MPa 油压下，两个不同温度对应的泄漏量的平均误差分别为25.6%和27.3%，虽然误差值相对较大，但是经分析，其泄漏量的绝对偏差值相对较小，在可接受范围内。

表2 试验结果与仿真结果误差分析表Tab.2 Error analysis of test results and simulation results

从上述密封圈的摩擦扭矩和泄漏量的试验结果与仿真分析结果对比可以看出，虽然理论值和试验值存在一定的偏差，但是总体来说变化趋势一致，理论值与实验值的差别在可接受范围内，一定程度上验证了本研究提出的考虑磨损的组合密封圈的摩擦扭矩和泄漏量预测模型，具有一定的实用性。

5 结论

对旋转动密封圈的磨损仿真和密封性能预测方法开展研究。针对组合旋转密封的材料力学特性，建立了双向流-固耦合数值求解模型和程序，并在流-固耦合数值求解过程中，引入材料磨损的计算，比较了旋转格莱圈磨损前、磨损后的润滑和密封性能。搭建了旋转动密封试验台，开展了不同转速和不同温度下的旋转动密封性能试验和耐久性试验。结果表明，提出的基于密封圈磨损仿真的泄漏量预测和摩擦力矩预测模型具有较好的精度。该密封性能仿真方法可应用在航空旋转密封性能分析中，为液压产品的密封设计和参数选择提供指导。