空间Z形管路液-固两相流冲蚀特性分析
2022-04-19孙键琳张忠义高培鑫
孙键琳, 张忠义, 何 彤, 石 岩, 高培鑫, 于 涛
(1.烟台大学 机电汽车工程学院, 山东 烟台 264005; 2.北京航空航天大学 自动化科学与电气工程学院, 北京 100191)
引言
管路输送系统是石油化工行业健康发展的基础,对保障国计民生具有重大战略意义。弯管作为在油气管路运输系统中最重要的结构之一, 却非常容易受到冲蚀磨损破坏。因其突然改变流体的运输路径,造成大量砂粒以不同的速度和角度对弯管外壁内轮廓进行冲撞导致弯管壁厚减薄,承压能力减弱导致爆管等危险发生[1]。管路系统尤其是弯管处的冲蚀破坏导致某井场在几年时间内发生了多起管路失效破坏,严重影响企业生产效率[2]。空间Z形管路是石油开采过程中最常见的管件单元,一般用来改变管道中流体的方向,由于其结构的特殊性,大大增加了管路失效的概率。如何精确地预测管路系统中最大的冲蚀磨损发生的位置,获取基础工况参数对弯头处的冲蚀磨损特性至关重要。
近年来,国内外的许多学者针对弯头冲蚀磨损问题进行了大量的研究,例如:ZENG等[3]研究了90°弯头在不同的冲击速度和冲击角度下,二次流、涡流和颗粒轨迹对弯管侵蚀的影响。LIU等[4]研究了表面粗糙度和固体质量流量对90°弯管冲蚀率的影响,进行了弯管壁面侵蚀的动力学研究。ZENG等[5]研究了材料为碳钢的弯管的冲蚀情况,通过引用阵列电极技术,分析了不同位置处的冲蚀磨损特性。DESALE等[6]分析了8种不同大小的石英颗粒对铝合金的冲蚀磨损影响,确定了粒径大小的改变对冲蚀磨损存在临界动能。KANNOJIYA等[7]提出了多种工况条件下管路系统冲蚀磨损的影响规律。ZHANG等[8]分析发现在石油运输过程中,弯管的布局方式和流体的参数均对弯管冲蚀位置有影响。FAROKHIPOUR等[9]研究了两种管路结构中含砂液的流动特性和冲蚀磨损规律,在抗冲蚀问题上对管路结构进行了优化。刘亚俊等[10]通过多相流分析,研究了不同压力与流体速度之间的关系。余建星等[11-12]通过研究管道的冲蚀损伤屈曲问题建立了更适合的深海输送管路模型,得出损伤参数以及管路结构参数对冲蚀的敏感性。龙新平等[13]通过对多种磨损模型进行计算评估得到影响磨损大的因素。冯志成等[14]针对Y形夹角不同的三通管汇的冲蚀规律进行了研究,通过Fluent对管的速度、黏度、粒目数等进行数值模拟分析。李翔等[15]通过对T形弯头流场分布情况及冲蚀严重的部位,得出了颗粒浓度和入口速度对T形管的冲蚀磨损特点。
目前研究管道模型多以局部弯管的单个弯头为主,对实际工况中出现的复杂的典型Z形管路冲蚀规律研究不够全面,特别是流体在经过弯头时,流场特性的变化会导致复杂的冲蚀磨损行为,而空间Z形管路流体方向会经过两次空间改变,冲蚀磨损特性更为复杂。本研究以空间Z形管路为研究对象,针对该管型两段弯管及结构的特殊性,对其冲蚀磨损位置及最大冲蚀点进行了研究,讨论了不同工况下最大冲蚀率和冲蚀区域的变化情况,为后续工程实践中高压管汇的冲蚀磨损预测及冲蚀位置的确定提供理论参考。
1 冲蚀模型数值模拟
1.1 几何模型及网格划分
本研究以典型的空间Z形管路为例进行分析,尺寸结构如图1所示,分析工况条件如表1所示。几何模型为空间异面布置,夹角为90°,上边为进口端,下边为出口端。1#、3#、5#为直管段,2#、4#为90°弯管段。
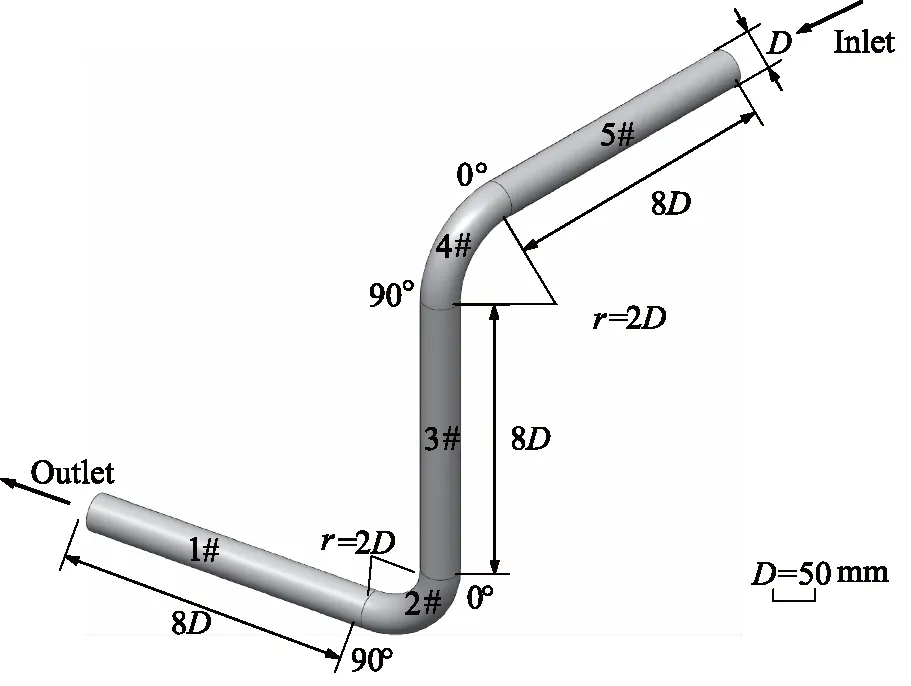
图1 三维模型示意图Fig.1 Schematic diagram of 3D model

表1 压裂液参数Tab.1 Fracturing fluid parameters
网格质量的好坏会直接或间接的影响仿真模拟的准确性,采用六面体非结构化网格并设置边界层,确保仿真结果的准确性。网格模型如图2所示。

图2 网格划分Fig.2 Mesh division
1.2 冲蚀磨损理论分析
根据压裂作业进程,弯管内部为复杂的液-固两相流空间紊流流场,设置水为连续相,固体粒子为压裂溶液的离散相,控制离散相的体积分数低于10%,这样就可以不计固体颗粒之间的碰撞影响,使粒子达到负荷流动模式[16-18]。因此针对流体中砂粒所占体积分数较小,选用DPM(Discrete Phase Model)模型计算可以更全面的分析各种参数对冲蚀磨损的影响。
1) 控制方程
空间管道内压裂液的流动遵循着物理守恒定律,结合牛顿第二定律,得到流体的控制方程如下[19-21]:
(1) 质量守恒的连续性方程:
(1)
(2) 动量方程:
(2)
(3)
(3) 能量方程:
(4)
式中,ρ—— 密度
t—— 时间
v—— 流体速度矢量
Vm—— 体积力
p—— 压力
τmn—— 应力张量
λ—— 导热系数
Sε—— 能量源
E—— 湍流耗散率
2) 冲蚀磨损模型
壁面冲蚀磨损的大小与多种因素有关,根据文献[12],本研究选用经典的冲蚀磨损模型进行分析,如式(5)所示:
(5)
式中,Rerosion—— 冲蚀磨损率
N—— 颗粒的数目
mn—— 质量流量
C(dn)=1.8×10-9—— 直径系数
θ—— 入射角
f(θ) —— 颗粒入射角度的计算函数
u—— 颗粒的速度
b(u) —— 颗粒的速度相关函数
ω—— 颗粒碰撞速率的计算函数,默认选取2.6
Aface—— 被冲蚀壁面的表面积
3) 湍流模型的选择
雷诺数大小是区分流体状态的依据,当雷诺数大于2300时,就可认定流体状态为湍流。其计算公式如下[22-23]:
(6)
式中,ρ1—— 液相的密度
V—— 液相流动的速度
D—— 流体管道的直径
η—— 液相的黏度
现在还没有较好的办法来分析和描述湍流的流动状态,仿真模拟软件中针对不同的湍流情况,可选用Laminar、k-e和k-omega等模型来进行分析。而通过阅读文献分析可知,k-e模型可以很好的模拟出液相流动状态。而Laminar模型的计算精度无法得到保证;而k-omega模型的有关参数较难获取。k-e湍流物理公式见式(7)[24]:
(7)

4) 壁面碰撞恢复系数
砂粒与管路内壁发生碰撞后,存在一定的能量散失,导致碰撞后的的粒子速度小于入射时的初始速度。砂粒撞击前后的能量耗散采用壁面恢复系数来定义,通过对比Wallance提到的不同方程,发现Forder等提出的冲击-反弹恢复系数方程比较符合本研究模型,方程如下[26]:
εt=0.998-0.029θ+(6.43e-4)θ2
-(3.56e-6)θ3
(8)
εn=0.993-0.0307θ+(4.75e-4)θ2
-(2.61e-6)θ3
(9)
式中,θ为颗粒冲击角。
2 数值结果分析
2.1 液相流动规律
伯努利方程揭示了机械能守恒定律,当液相速度改变后,液相的压力就会随之改变,且改变的大小幅度相同,选取1.1节设置的管路流体参数,通过计算,得到图3~图5所示的相关云图。

图3 速度矢量云图Fig.3 Speed vector cloud diagram
由图3速度矢量云图可知,由于管路“二次流“现象导致流体在流经弯管时,凸壁处流速增大,而外壁处流速受阻减缓,形成速度差。
由图4压力云图可以看出,沿着液相流动方向从进口端到出口端压力逐渐减小,在弯管处,压力值与速度值成反比关系,流体在凹壁处改变方向,导致流体压力增加,而凸壁处因流速较快导致压力较小。

图4 压力云图Fig.4 Pressure cloud diagram
由图5可以看出,在管道入口直管段,稳态流体携带砂粒呈直线式运动;当流体流经弯头处时,连续相受“二次流”影响,砂粒在弯头处运动发生不规则变化,在弯管进口端:因凹壁处压力大,压裂液压缩,而凸壁处流速快,压裂液舒张,使凹壁处形成涡流区(A区域);在弯管出口端:流体碰撞折返,导致局部B区域因压差和速度差形成凸壁涡流区;因此大量砂粒在4#弯管处集中通过弯管出口90°外壁处和直管段相邻处;而砂粒在进入3#直管段后流动状态相对稳定,大量砂粒沿外壁垂直向下,在流经2#弯管时,大量砂粒撞击进口端前部改变方向,导致2#弯管段的两个涡流区域发生前移,砂粒集中流动区域发生改变,在弯管处受离心力和流速的共同影响,在弯管出口端粒子轨迹出现旋转向内的旋转流现象。

图5 粒子轨迹云图Fig.5 Cloud diagram of particle trajectory
2.2 冲蚀磨损特征分析
取离散相颗粒密度为ρ=2650 kg/m3,颗粒粒径d=0.45 mm,黏度η=0.001 Pa·s,流速为v=20 m/s。通过仿真分析,得到弯管冲蚀区域如图6所示。

图6 冲蚀云图Fig.6 Erosion cloud map
由图6可知,压裂液对管汇的冲蚀主要发生在2#、4#两处弯管区域,通过图6对比两段弯管可知,弯管段比直管段更容易受到侵蚀,而在弯管处,由于砂粒受到离心力和局部涡流区的影响,使管汇外壁比内壁更容易受到撞击从而造成严重的侵蚀磨损。
由图7可知,4#弯管在0~10°范围内没有出现冲蚀现象,而70°~90°位置的冲蚀强度最大。原因是颗粒在进入弯管部分后,由于流体速度方向发生改变且受到A,B两个区域的涡流影响,外侧砂粒受到流体拽力的影响,流动方向向内侧偏移,使大量颗粒对弯管壁面进行正面撞击,70°~90°的位置粒子数目多,流速快,冲蚀磨损加剧。

图7 弯管角度图Fig.7 Angle view of elbow
而2#弯管的主要冲蚀磨损位置位于弯管0°~30°和70°~90°的位置,粒子轨迹揭示了大量砂粒沿直管段垂直下落,弯管受到砂粒离心力以及重力作用,对0°~30°的范围内的弯管壁面进行猛烈撞击,造成该弯管入口端冲蚀严重,而随着“二次流”和局部涡流的影响,部分粒子在撞击后又随流体运动趋势撞向弯管高角度位置,从而造成在弯管70°~90°的位置也出现严重的冲蚀区域。但2#弯管主要冲蚀区域位于弯管中心轴截面的一侧而非正中间或均匀分布两侧,这是因为凸壁涡流区域B使得4#弯头外壁侧会形成一个明显的流体挤压面,大部分粒子会沿外管壁向下对2#弯管单侧外壁面进行剪切作用,造成严重的切削磨损。而由于2#弯管的出口处存在二次流漩涡,使得出口段直管段也会产生一定程度的冲蚀磨损。
3 不同参数对冲蚀的影响分析
3.1 流速对冲蚀的影响
流速是造成管路系统冲蚀磨损最为重要的因素之一,为了适应大排量、高效率的开采作业,高压管汇的输送量也在不断加大,通过数值模拟分析,选取5种压裂液流速,v分别为20,25,30,35,40 m/s,计算得到两个弯头冲蚀严重的区域内,流速与冲蚀率的关系,如图8所示。
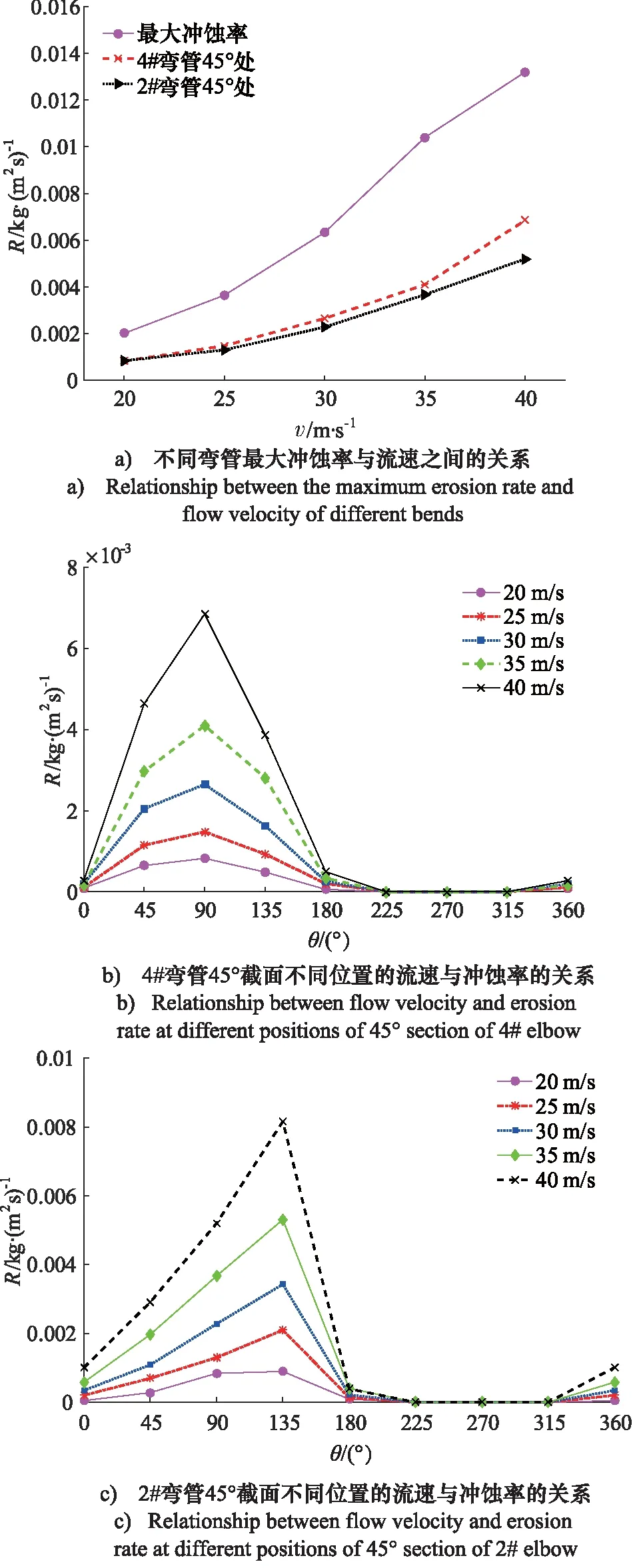
图8 流速与冲蚀率的关系Fig.8 Relationship between flow velocity and erosion rate
通过对不同流速的比较分析可知:流速的改变对弯管冲蚀位置的影响较小,2#弯管最大冲蚀位置发生在进口端0°~30°远离进口方向的一侧,4#弯管最大冲蚀位置为弯管90°左右的外拱壁面两侧,但冲蚀磨损程度随着流速的增加越来越严重。流速的增加导致冲蚀磨损区域大小向四周扩散,流速过大会直接造成冲蚀磨损区域超过180°分布到凸壁侧。当流速超过30 m/s后,最大冲蚀增长速率加快,流速对管路的最大冲蚀率成指数形式激增。4#弯管段相比于2#弯管段冲蚀率相对较低,4#弯管的最大冲蚀区域位于弯管下游出口端,2#弯管呈竖直-水平的方式分布,因在3#直管段产生砂粒集中运动和重力与离心力的共同作用,进一步加快了砂粒对管壁的冲击碰撞,而管壁的冲蚀磨损受流速的影响较大,流速的增加是影响冲蚀磨损的重要因素之一,减小流速可以有效降低冲蚀磨损速率。
3.2 颗粒直径对冲蚀的影响
颗粒直径对实际施工过程中管路的冲蚀磨损影响也尤为严重,本研究选取不同的颗粒数目进行分析,如表2所示。

表2 颗粒数目与粒径的关系Tab.2 Relationship between number of particles and particle size
“尺寸效应”指的是粒目数减少,粒径尺寸增加,导致砂粒与壁面接触产生的切削作用增加, 在超过临界尺寸后,粒径对冲蚀磨损的影响加剧提升;而“数量效应”表示当砂粒直径减小,相同体积内砂粒数目增加,导致在相同条件下颗粒对管壁的冲击数量增加,冲蚀率增加[16]。在浓度不变的情况下, 粒径的变化主要揭示了两种效应叠加的结果,两种效应的主导地位在不同的区域位置也有所不同,粒径也是影响冲蚀率的重要因素之一。
由图9a可知,当粒子数目从70目降低到40目时,最大冲蚀率与不同弯头处固定点的冲蚀速率变化都相对平缓,这是由于粒子数目多造成粒子间的相互碰撞次数增加,损失了大量的能量,使得砂粒对管壁的撞击强度减小。当粒目数缩小到30目后,颗粒质量增加,在相同的速度条件下,质量大的砂粒动能大,对管壁的冲击强度增加导致冲蚀速率加快。图9b和图9c分别表示了两段弯管相同位置处的冲蚀率随着粒径和角度变化的冲蚀规律。4#弯管处流动状态经过一次改变,冲蚀率与粒径之间的变化规律相对均匀,随着粒径的增加,冲蚀率逐渐增加;2#弯管处因受到两次流体状态的变化,粒径变化对弯管处冲蚀率的影响规律呈现先增大后减小的趋势,这是由于大粒径的砂粒在经过第一段弯管时对弯管的撞击和颗粒之间的相互碰撞使得颗粒破碎,颗粒数目增加,粒径减小,再经过直管段和第二段弯管后,颗粒直径会越来越小,碰撞后的小颗粒会附着在管壁冲蚀凹坑处,使后续粒子对管壁的冲击影响降低。

图9 不同粒径与冲蚀率的关系Fig.9 Relationship between different particle sizes and erosion rate
3.3 质量流量对冲蚀的影响
本节选取3, 5, 7, 9, 11, 13 kg/s这6个不同的质量流量进行分析,得到的结果如图10所示。
由图10a可知,弯管处冲蚀率随着质量流量的增加而增大。在3~7 kg/s的范围内,冲蚀率呈线性正相关趋势平稳增长;在7~13 kg/s的范围内,最大冲蚀率的增速随着质量流量的增加逐渐加快。这是因为随着质量流量的增加,砂粒数目变多,增加了砂粒与弯管壁面的接触面积,加重了冲蚀磨损。从入口进入的粒子流,在没受到外界作用力的情况下,均匀冲撞在4#号弯管处,但在经过3#直管段时,粒子间的相互作用以及反弹角度的不同,造成了粒子乱流,低质量流量的条件下,增加了粒子间的相互碰撞损失的能量远小于砂粒碰撞壁面所消耗的能量,导致4#弯管处的冲蚀率会小于2#弯管。 当质量流量超过11 kg/s时, 2#弯管处的最大冲蚀率发生不规则改变,这是因为随着质量流量的增大,在经过3#直管段的过程中,因为粒子紊流加剧了粒子间的碰撞,使得砂粒破碎,导致单位时间内与壁面接触的砂粒数目增加,冲蚀率快速增长。由图10c可以看出, 2#弯管处冲蚀位置没有明显的向135°方向偏移,是因为粒子间的相互碰撞破碎,粒子数目急剧增多,在“二次流”的影响下,弯头管壁内侧处大量地粒子堆积导致冲蚀破坏现象减弱。

图10 不同粒径与冲蚀率的关系Fig.10 Relationship between different particle sizes and erosion rate
3.4 黏度对冲蚀的影响
不同黏度的液-固两相流对管路冲蚀磨损也有影响,选取7种压裂液黏度,通过仿真分析,结果如图11所示。

图11 不同黏度与冲蚀率的关系Fig.11 Relationship between different viscosities and erosion rate
由图11a可以看出,冲蚀率随着黏度的增加而减小。黏度的增加导致颗粒对液体的附着性增强,使得颗粒与流体的流动方向和状态逐渐一致,减小了颗粒与管壁接触产生的冲蚀磨损。通过图11b和图11c可以看出,2#弯管固定点的冲蚀磨损速率随着黏度的增加先增后降,而4#弯管段固定点的冲蚀率随着黏度的增加逐渐降低。这是因为随着黏度的增加,颗粒对弯头的碰撞位置发生改变。
3.5 重力对冲蚀的影响
在油气开采传输过程中,由于管道线路走向的选择较为复杂,为了验证重力对弯管冲蚀磨损的影响,本节选取压裂液从上往下流和从下往上流两种方式:
由图13可知,2#弯管和4#弯管在不同流向状态下的冲蚀磨损变化情况,液相流动方向的差异会影响冲蚀磨损速率。管路内介质流动方向从上往下流(图12a)时,最大冲蚀率为2.01 e-3 kg/(m2·s),管路内介质流动方向从下往上流(图12b)时,最大冲蚀率为2.21 e-3 kg/(m2·s)。冲蚀磨损最大发生在从下往上流的管路中,此时在经过3#直管段时,重力与流动方向相反。这是由于砂粒向上运动时,因重力作用使其运动变缓,使局部砂粒聚集导致冲蚀磨损增大。由上述分析可知,开采现场合理的管路布局方式将影响弯管冲蚀磨损速率。
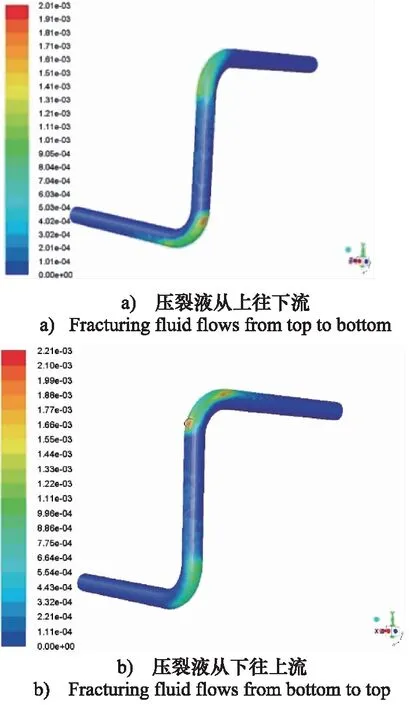
图12 压裂液流向示意图Fig.12 Schematic diagram of fracturing fluid flow

图13 不同方式下冲蚀率比较Fig.13 Comparison of erosion rates under different methods
4 结论
本研究对工程实际中典型的空间Z形管路进行了分析, 并分析了不同工况下的冲蚀位置变化和不同工况对冲蚀磨损预测的影响规律,结论如下:
(1) 沿液相流动方向的第一段弯管, 其最大冲蚀位置在弯管出口处与直管段连接部位;第二段弯头的主要冲蚀区域发生在其入口端0°~30°位置和靠近出口端的70°~90°两个位置;
(2) 整体管路的进口端弯头冲蚀率小于出口端弯头冲蚀率,进口端弯头冲蚀位置沿管路中轴线对称分布,出口端弯头的冲蚀位置主要集中在该弯管远离整体管路进口方向的一侧;
(3) 空间Z形管路的最大冲蚀速率随着携砂液的流速、颗粒直径、质量流量的增加而增大,随着黏度的增加而减小,其中流速对冲蚀磨损速率的影响最严重。在工程实际中,主要考虑流速对管路冲蚀磨损的影响,适当减小流速、粒径、质量流量,适当增加流体黏度,都可以减小Z形管路的冲蚀磨损速率;
(4) 不同的进出口方向,冲蚀磨损破坏最严重的是从下往上流的情况。这是由于砂粒向上运动时,因重力作用使其运动变缓,使局部砂粒聚集导致冲蚀磨损增大。
通过本研究的分析,获得了不同工况对冲蚀磨损的影响规律,为实际管路的设计和布局提供参考,在工程实际生产过程中,应综合考虑不同工况和冲蚀磨损的影响因素,合理调整各个参数,减小弯管冲蚀磨损速率。
