双向液压式调速器系统数学建模与仿真

汤斯佳， 陶邦明， 董 群， 蒋君侠

(1.惠阳航空螺旋桨有限责任公司， 河北 保定 071025； 2.浙江大学 机械工程学院， 浙江 杭州 310027)

引言

飞机螺旋桨的调速器系统是在飞机飞行过程中起到调节螺旋桨桨叶角，保持发动机转速恒定作用的重要装置，要研制螺旋桨飞机，就离不开对调速器系统的研究，特别是液压式调速器系统具有很高的研究价值。

国外对调速器系统的研究开始较早。1928年HELE-SHAW H S提出了液压式飞机螺旋桨调速系统[1]；1937年MARTIN E提出了恒速螺旋桨， 对液压式调速系统进行了细致的说明[2]；1984年STEINETZ B提出了混合动力牵引的先进螺旋桨调速系统[3]；1985年ANDERSON R D对现有的调速系统进行了结构优化[4]。这些研究都对调速器系统进行了详尽的论述，但都没有涉及其具体结构的数学建模，同时因为时代因素也未与Simulink等仿真软件结合对调速系统的动态特性进行分析。

相比国外，国内对于飞机螺旋桨调速系统的研究起步晚，相关研究较少，其中王凯等[5]对SR20飞机螺旋桨系统工作原理及典型故障分析；林建平等[6]对飞机螺旋桨液压调速系统的流量特性进行了数学建模和仿真分析；关世超[7]对DA42NG型飞机螺旋桨变距工作原理进行介绍。目前国内关于调速器系统方面的研究主要集中在柴油机调速器和船用螺旋桨调速器方面。陈坚[8]进行了船用发电柴油机调速器的数学建模；谢清程等[9]对船舶螺旋桨调距速率特性进行了分析。郑安宾等[10]对几种有代表性的船用调距桨液压系统进行了简要分析；贾富等[11]对船舶螺旋桨进行了数学建模。也有一些比较分散的相关研究，段登燕等[12]对无人机的变距螺旋桨进行了系统功率优化控制。闻德生等[13]通过AMESim对变量泵的新式调速回路的特性进行了分析和实验；罗艳蕾等[14]利用MATLAB进行微分方程求解得到了调速平衡回路的动态特性。费望龙等[15]设计了风力发电机的液压变桨系统。这些研究的总体数量少，同时对具体结构的研究和分析较缺乏。

本研究以螺旋桨飞机的双向液压式调速器系统为研究对象，根据牛顿力学和流量连续方程建立调速器系统的数学模型，利用Simulink与数学模型结合进行仿真，对调速器系统的动态特性进行完整分析。

1 双向液压式调速器系统结构原理

如图1所示为双向液压式调速器系统的结构，调速器作为核心部件通过飞块支架与发动机连接，其压力油路、回油路与液压控制系统相连通，液压控制系统控制油路油压，大距油路与液压缸连通，控制活门为控制油路的阀芯，液压缸通过活塞与螺旋桨连接。

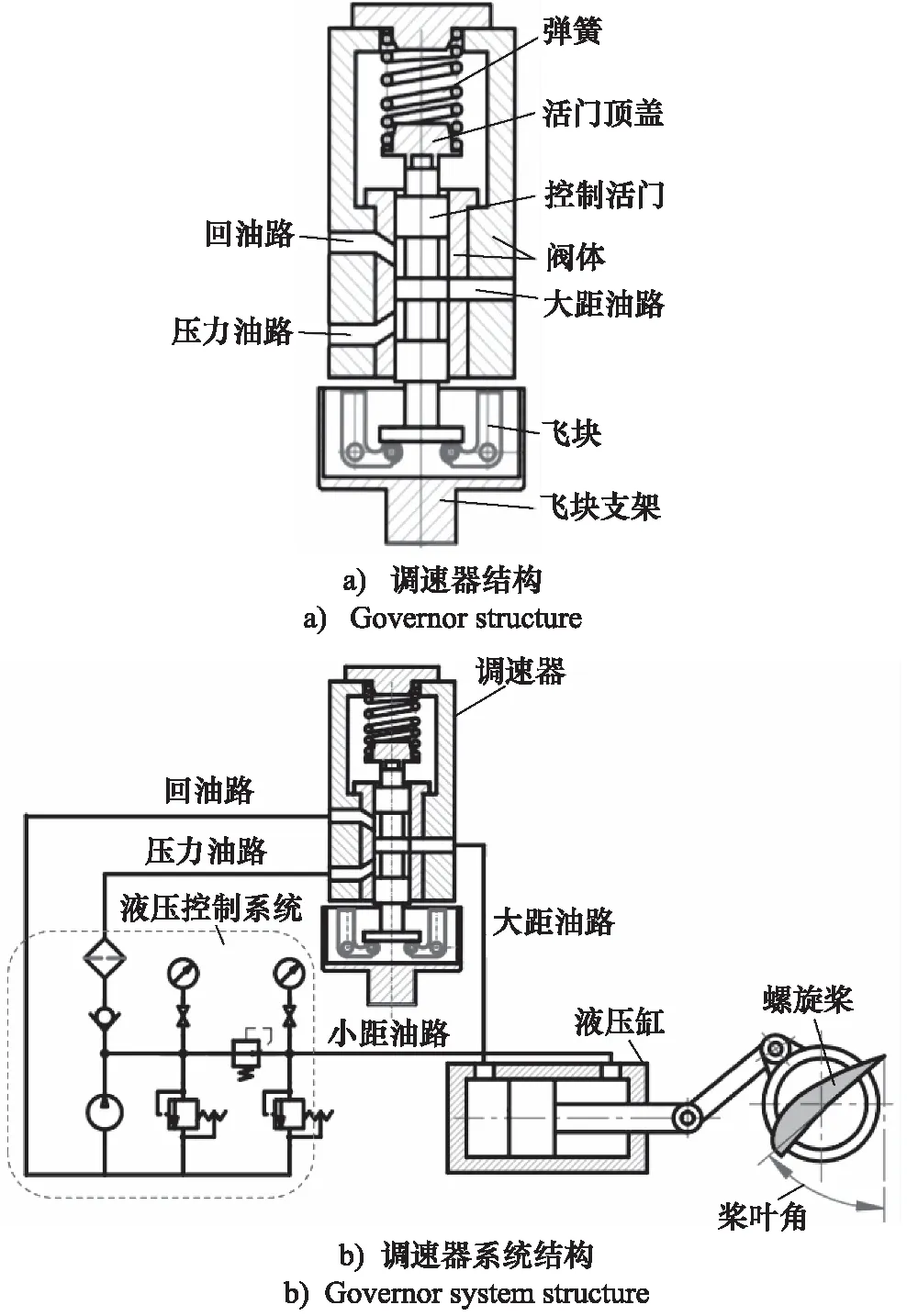
图1 调速器及其系统结构图Fig.1 Governor and its system structure diagram

调速器作为调速系统的核心部件，以飞块作为敏感元件，感受发动机的转速变化，并将其转速变化量转化为相应的控制活门的位移，再通过阀芯阀体的液压功率放大功能改变调速器输出的压力信号，通过液压缸运动改变螺旋桨的桨叶角，使螺旋桨在给定转速下的旋转阻力矩与发动机轴扭矩相平衡，来保证发动机的转速恒定。

当飞机飞行状态稳定时，发动机的输出功率与螺旋桨吸收的功率相等，发动机传递给调速器的为平衡转速。在平衡转速下，控制活门受力平衡不发生运动，控制活门中部凸肩封闭大距油路，从而螺旋桨桨叶角保持不变。

当因飞行状态变化造成螺旋桨吸收的功率与发动机的输出功率不平衡时，发动机的转速会发生变化，偏离平衡转速，这时，调速器将自动使发动机转速恢复到平衡转速。在转速增大时，飞块因受离心力抬起控制活门，压力油进入大距油路，液压缸向右运动使桨叶角增大，转速下降，直至恢复平衡转速，大距油路重新被控制活门中部凸肩封闭为止；在转速减小时，控制活门下移，大距油路与回油路相通，液压缸向左运动使桨叶角减小，转速上升，直至恢复平衡转速为止。

2 双向液压式调速器系统数学建模

2.1 控制活门力-运动数学模型

控制活门顶边受到弹簧力，底边受到飞块施加的力，中间受到流体作用力，如图2所示。

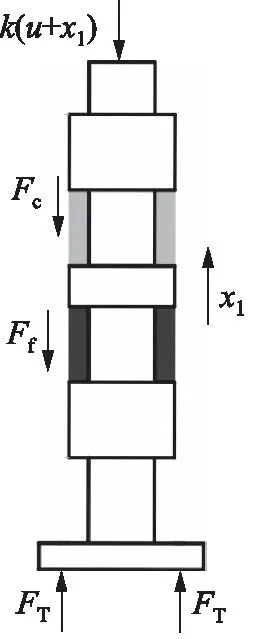
图2 控制活门受力图Fig.2 Control valve spool force diagram

则根据牛顿第二定律，建立受力与运动的关系，得到控制活门的动态运动方程为[16-18]：

(1)

式中，FT—— 单个飞块对控制活门的作用力

k—— 调速器弹簧的弹性系数

u—— 平衡状态下调速器弹簧预压缩量

x1—— 控制活门相对于平衡位置的位移

Fc—— 黏性摩擦力

Ff—— 液动力

m2—— 控制活门质量

1) 飞块作用力FT求解

飞块是调速器感应速度的元件，其结构如图3所示。其主要作用为通过离心原理以及特殊的结构将转速大小转变为向上的推力大小。

图3中，ω为飞块角速度；L为飞块与控制活门接触点到飞块自身旋转轴的距离，L=11 mm；Y为飞块质心到飞块自身旋转轴的距离，Y=5.63 mm；R为飞块质心到飞块支架旋转轴的距离，R=17.85 mm；FR为作用于飞块质心(图中空心圆点为飞块质心)的离心力。

调速器运行时，作用在单个飞块的离心力为：

FR=mRω2

(2)

式中,m—— 单个飞块质量。

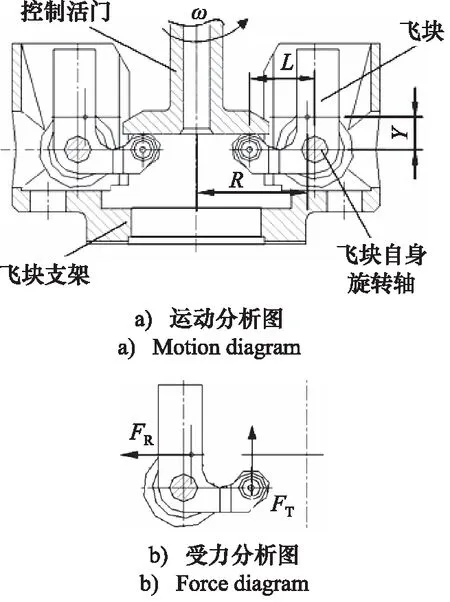
图3 飞块运动与受力图Fig.3 Flying block motion and force diagram

根据杠杆定律，得单个飞块提供的向上推力FT为：

FT=CFR

(3)

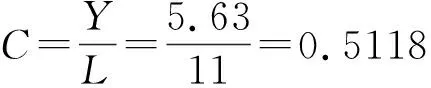
联立式(2)、式(3)，结合飞块转速与飞块角速度的关系，得：

(4)

式中，n(t) —— 发动机的转速。

2) 弹簧预紧压缩量求解

平衡状态下调速弹簧预压缩量u可由设定的螺旋桨转速计算得到：

(5)

式中，ω0—— 平衡角速度，ω0=2πn0

n0—— 平衡时发动机转速，n0=5670 r/min

代入所有参数数值，解得：

u=6.98 mm

3) 黏性摩擦力求解

由于安装时阀芯与阀体之间存在间隙，二者间有液体流动，存在黏性摩擦力，其方向始终与速度相反。

(6)

式中，B—— 黏性阻尼系数，其值由间隙大小、阀体直径和液体黏度共同确定[16]，本调速器为5 N/(m·s-1)。

4) 液动力求解

液动力是流体通过阀口时作用在阀芯上的力，分为稳态液动力和瞬态液动力：

Ff=Fs+Fi

(7)

式中，Fs—— 稳态液动力

Fi—— 瞬态液动力

稳态液动力求解公式[19-21]：

Fs=2CvCdwx1Δp1cosθ

(8)

式中，Cv—— 流速系数，一般取0.98～0.99，此处取0.98

Cd—— 流量系数，一般取0.6～0.8，此处取0.6

w—— 阀口节流边周长，w=πd=50.265 mm，d为控制活门与阀体配合部分的外径，d=16 mm

Δp1—— 阀口前后的稳态压差，考虑到稳定情况下大距油路的油压变化，此处Δp1=0.01 MPa

θ—— 射流方向角，对于理想滑阀一般取69°

瞬态液动力求解公式[19-21]：

(9)

式中,L1—— 阀口距离，L1=6.1 mm

ρ—— 油液密度

Δp2—— 阀口前后的瞬态压差，考虑到瞬态情况下大距油路的油压变化，此处Δp2=3.73 MPa

2.2 液压缸与螺旋桨的力-运动数学模型

大距油路的油液进入液压缸推动活塞运动，活塞通过连杆滑块机构与螺旋桨相连接，使桨叶角变化，如图4所示。

图4 液压缸-螺旋桨结构图Fig.4 Hydraulic cylinder-propeller structure diagram

图4中：p2为大距油路油压；p4为小距油路油压；θ为螺旋桨角度；其余均为对应尺寸的长度。

忽略连杆运动对液压缸的作用力，则根据牛顿第二定律建立液压缸的运动数学模型，有：

(10)

式中，A2—— 大距油作用在活塞上的面积

A4—— 小距油作用面积

m2—— 活塞质量

x2—— 活塞位移

液压缸运动通过连杆机构改变螺旋桨角度，根据几何知识，有：

(11)

(12)

联立式(11)、式(12)解得螺旋桨角度为：

(13)

式中，b=9 mm；l1=45.75 mm；l2=71.8 mm；x0=85.6 mm。

2.3 流量数学模型

当控制活门产生上下位移时，与阀体产生交错，大距油路的槽口开启，如图5所示。

根据流量连续方程建立大距油路与压力油路、回油路的流量数学模型[22]：

(14)

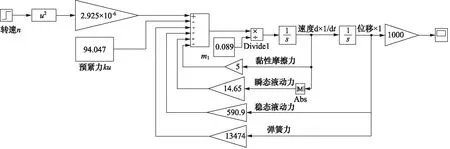
图6 控制活门仿真模型Fig.6 Control valve spool simulation model

式中，Qf—— 阀口流量

Qx—— 泄漏流量

E—— 油液弹性模量，E=1200 MPa

当控制活门沿x1正方向移动，V=V1，V1为出口至大距油路的管路容腔体积；p=p1，p1为压力油路油压。当控制活门沿x1负方向移动，V=V2，V2为大距油路至回油路的管路容腔体积；p=p2。

阀口流量为：

(15)

式中， Δp—— 阀口油压差值，取正值。

其中，大距油路的油压求解需要使用液体压缩公式：

(16)

式中， ΔV—— 大距油路体积变化量。

3 双向液压式调速器Simulink仿真

MATLAB/Simulink可根据数学模型搭建仿真模型来对二阶微分方程进行分析。利用MATLAB/Simulink建立仿真模型分析，通过调整不同参数来找到影响调速器运动的主要因素，从而有方向性地寻找优化的方向。

3.1 控制活门运动数学模型仿真

将表1的参数代入式(1)，得到控制活门的数学模型如下：

(17)

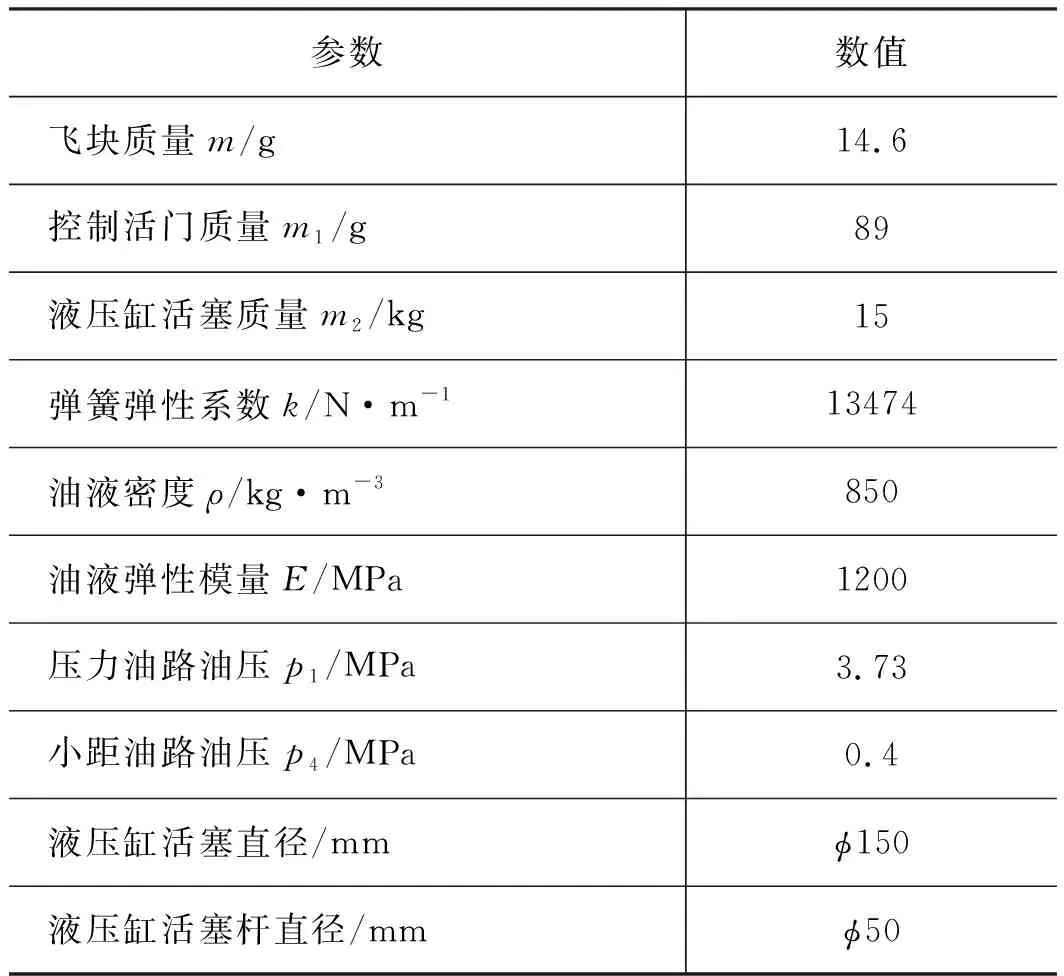
表1 螺旋桨调速系统主要参数Tab.1 Propeller governor system main parameters

根据式(17)，搭建如图6所示的Simulink仿真模型；输入如图7a所示的转速，得到控制活门的位移曲线如图7b所示。

图7 发动机转速发生变化时控制活门位移的变化Fig.7 Control valve spool displacement due to rotational speed changes

从控制活门仿真结果可以看出：当转速为设定的平衡转速5670 r/min时，活门位移为0 mm，此时控制活门不运动，大距油路无流量进入；当转速突然增大100 r/min时，控制活门位移迅速增大并发生短时间的振动，之后恢复平衡，此时弹簧力与液动力、飞块作用力平衡；当转速减小时，也可以得到相似的曲线。

3.2 整个调速器系统的数学模型仿真

添加油路、液压缸和螺旋桨的数学模型，得到整个调速器系统的数学模型，如图8所示。

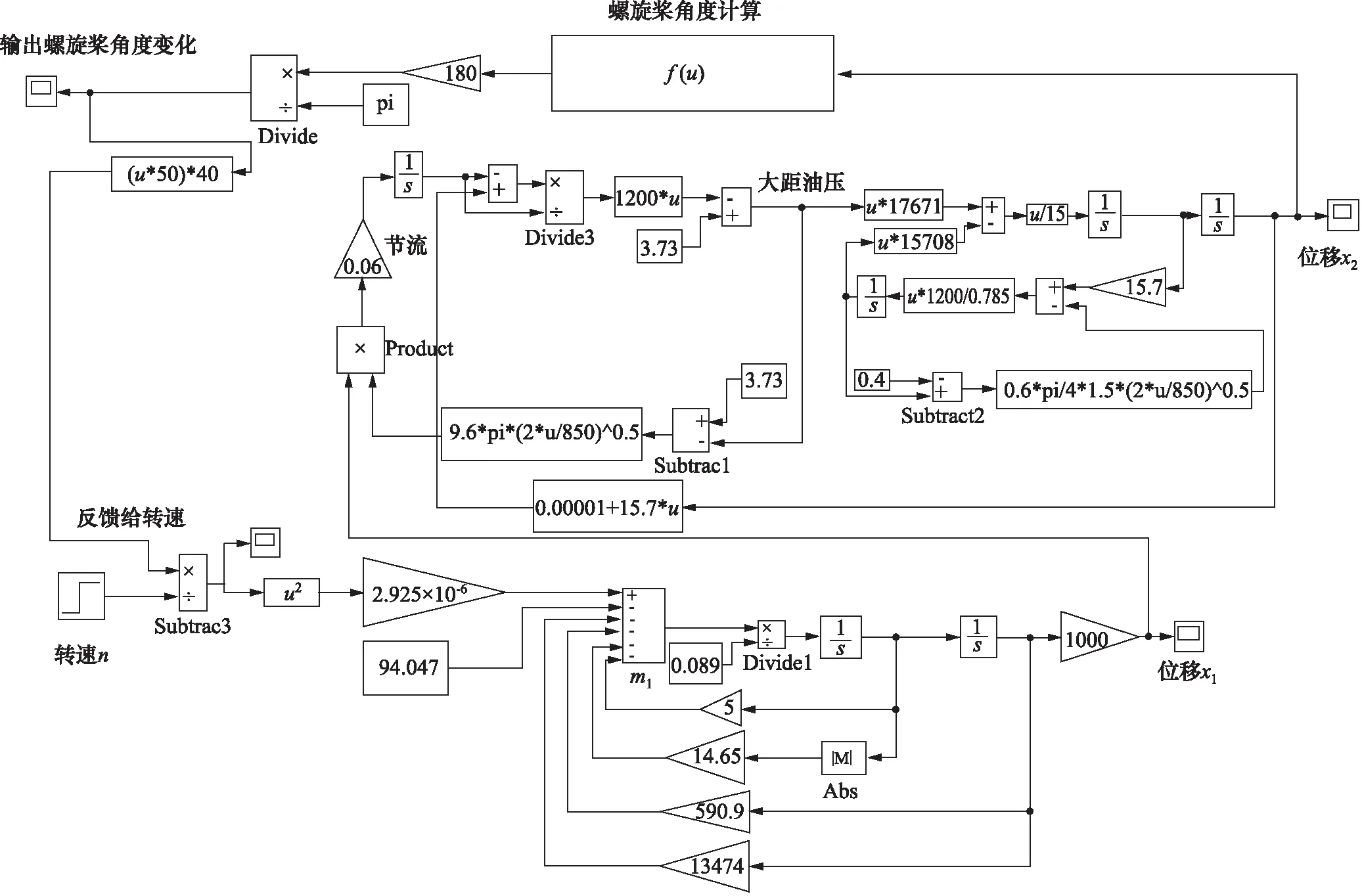
图8 整个调速器系统仿真模型Fig.8 Whole governor system simulation model

其中控制活门输出位移控制大距油路流量和油压，大距油路输出的大距油压控制液压缸运动；液压缸的活塞位移控制螺旋桨角度，螺旋桨角度通过螺旋桨与空气阻力的关系改变发动机负载，从而反馈控制发动机转速，最终得到的调速器系统仿真结果如图9所示。

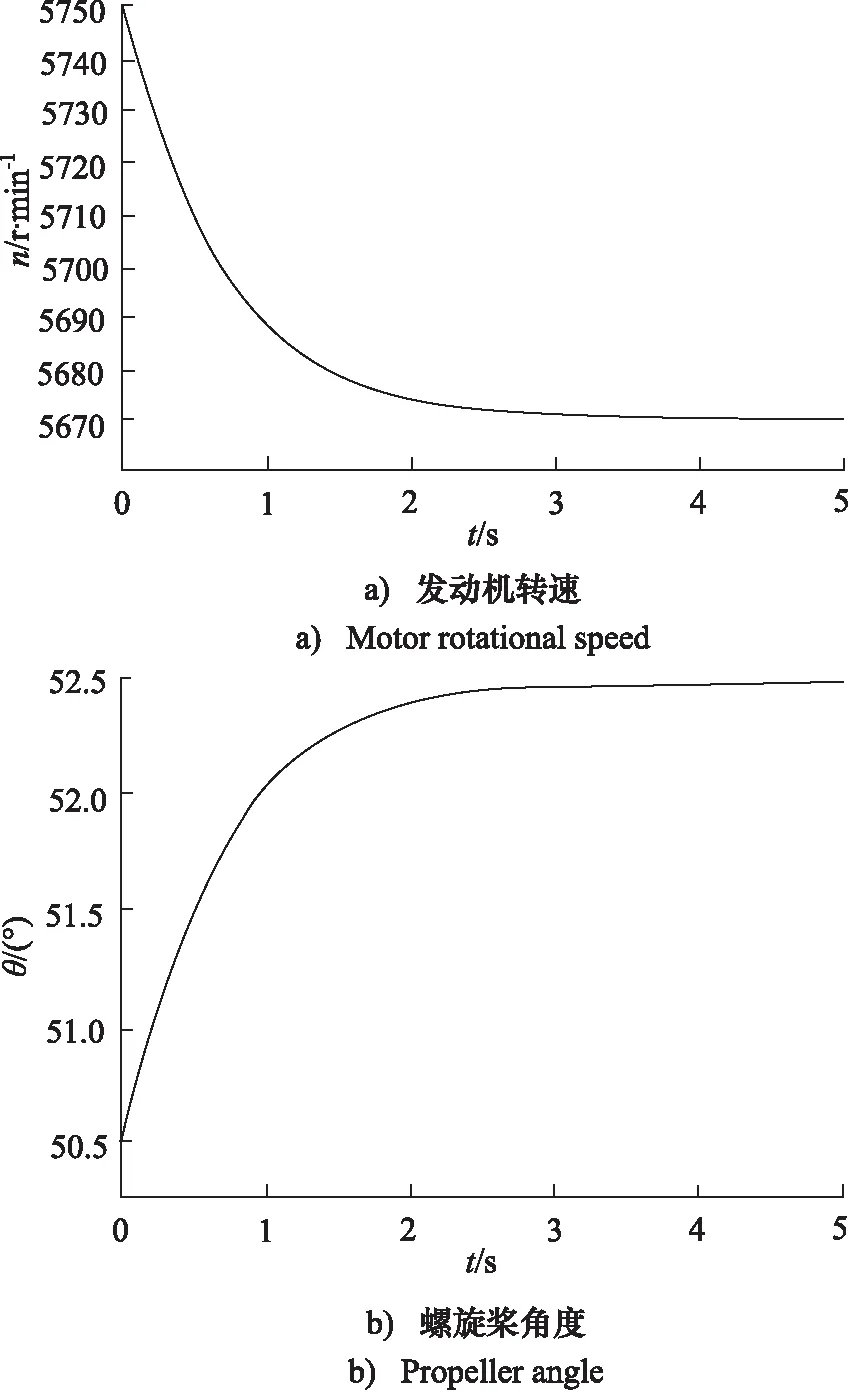
图9 发动机转速变化时转速变化和螺旋桨角度变化Fig.9 Motor rotational speed and propeller angle diagram due to motor speed changes

从整个调速器系统仿真结果可以看出：转速很快恢复到平衡转速，之后保持不变。螺旋桨角度增大到一定值后也保持不变，因为此时螺旋桨的功率与发动机的功率一致，转速已经平衡。

4 结论

结合某型螺旋桨飞机双向液压式调速器系统具体结构，对调速器系统在不同发动机转速变化下的工作原理进行分析，通过力学和数学分析，搭建出控制活门、液压缸和螺旋桨的运动数学模型，以及系统油路的流量数学模型。结合真实可靠的参数值，利用MATLAB/Simulink软件进行控制活门运动仿真和整个调速器系统仿真。仿真实验结果表明： 发动机转速变化会导致控制活门的位移发生振荡，同时，在完整调速器系统作用下， 转速偏离后发动机的转速会很快恢复平衡值，并与螺旋桨角度发生的变化相对应，证明了所建立的系统数学模型的有效性及可行性，并为后续设计优化提供了思路。