图形思维,计算可视
——以“图形巧运算——水下城堡”为例的思维可视化研究
2022-04-19江苏省南京市江宁上坊新城小学吴晓霞
江苏省南京市江宁上坊新城小学 吴晓霞
【案例背景】
作为学科核心素养的计算思维在程序教学中得到重视与积极的实践,而如何在非程序教学中体现图形思维的价值,值得广大教师关注和研究。培养图形分析思维是要帮助学生在图形信息的生活中,学会分析归类、总结规律、提升系统。但是,在实际教学中,教师普遍存在着重“技能训练”而轻“图形思维”的理解偏差。
一、重操作技能培养,轻图形思维训练
信息课堂中,教师比较重视学生画图软件操作技能的培养,操作讲解多,问题分析少;基础训练多,思维理解少。课堂中教师对图形分析思维并不关注,为了画图而画图,使学生无法感悟技术、思维与艺术的统一。
二、重操作作品讲解,轻图形思维分析
画图模块学习的终极目标是运用“图形思维分析”来解决日常生活中的实际问题。在常规教学中,教师的画图模块学习变成了“电子美术课”。课堂中,学生机械地模仿、练习,填鸭式的软件操作,使学生忽视了图形的分析、归类、内化等过程,学生无法在感知图形逻辑思维的过程中,体会图形设计中的逻辑思维。
【案例描述】
一、图形游戏,课中有“乐”
【片段一】游戏导入 引发需求(如图1)

图1
师:今天老师给大家带来一个游戏,请大家玩一玩,选出上面哪个图形不同于其他图形?
学生活动:学生开心地玩游戏,并观察找出不同图形,初步感知组合图形。
……
师:你来说一说答案。
生:它们都是单个图形,而其他的图形都是两个图形组合的。
师:图形都是怎么组合的?有什么规律?
二、图形组合,心中有“类”
【片段二】图形思维 图形组合
师:水王子的水晶窗被破坏了,你们能把它修复吗?
学件:学生桌面上提供半成品《水下城堡》(如图2)。
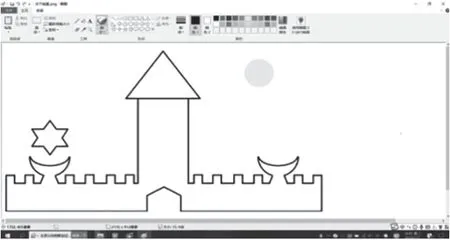
图2
师:请你来说一说你是怎么画的。
生:先画一个长方形,再把它分成八个。(在说的同时已经有学生发现问题)
师:你是先绘制整体,再分割为局部,请仔细观察八个水晶窗户,谁能说说它们有什么特点?他的这幅图有什么问题?(暗指学生出现的不平均问题)
生:水王子要求八个水晶窗户大小相同,并且还提醒需要最快速。
师:相同,我们可以怎么做?
生:复制。
师:对,可以先绘制局部,复制一个,然后怎么操作?
生:添加到图形中,合成整体。
师:添加到图形合成一个,这就是组合图形的添加(板书:图形添加),但是怎么复制最快速呢?(顺势引导图形迭代思维的选择方法)
生:先复制一个变为两个,再复制两个变为四个,再复制四个变为八个。
师:你们可以再次进行操作了吗?
生:可以!
学生活动:进行绘制(如图3),理解叠加选择与递增,进行组合操作,感受图形组合运算递增的神奇。
图3
师:月牙宝石被盗走了,你们能帮水王子找回来吗?
师:宝石由月亮倒影形成,水王子提醒月牙宝石是什么形状的。
生:圆形的一部分。(学生感到为难,曲线工具很难画出,橡皮擦又擦不圆)
师:如何利用现有圆形月亮,修改图形,使其变为月牙宝石形状呢?我们就要思考月牙的形成是由于月相变化,仔细观察月相变化动画,看谁有一双火眼金睛可以找到方法。
教师播放Flash动画(如图4)启发:利用月相变化图启发学生思考。

图4
师:如果遮住的部分颜色为背景颜色,就在图形中减去(板书:图形减去)变为月牙形。你们可以再次进行操作了吗?
生:可以!

图5
师:魔法船被封印到三张魔法卡片(如图6)了,谁能找到它?

图6
生:它在第二张图的中间。
师:具体位置在哪里?(引导学生发现形状交叉)
生:在椭圆形和六角星相交的地方。
……
师:不但要交叉还要注意椭圆只能有边框,并且将外面的颜色都填充为背景色,其他颜色填充图形交叉部分,魔法船就是图形交叉的部分(板书:图形交叉)。你们可以再次进行操作了吗?
生:可以!
学生活动:在原有图形的基础上,进行绘制,利用形状进行改进,实现图形交叉,填充颜色解封魔法船。(如图7)

图7
三、项目牵引,脑中有“案”
【片段三】图形思维 项目方案
师:水下城堡没有了色彩,失去了往日的活力,城堡里的生物都藏起来了。你们可不可以帮助他们设计出个性的水下城堡,让它恢复往日的生机?
生:可以。
师:请取出你们的设计单,选择设计方法,拿出设计方案,画出设计草图,进行图形制作。(提醒学生合理、灵活使用知识解决实际问题)
学生活动:拿出学习单,勾选适合的设计方法,并绘制设计草图(如图8)。
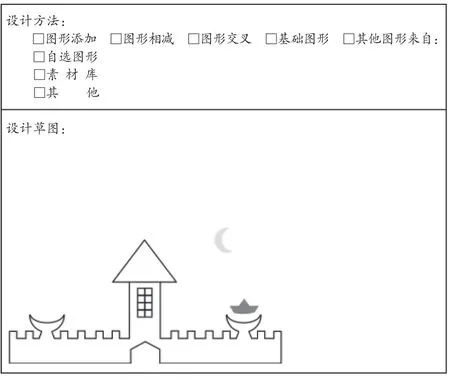
图8 水下城堡个性设计方案
师:生物避难所的素材库中,螃蟹和龙虾丢失了引以为傲的钳子,其他生物也受到了不同程度的伤害,请你们选择想添加的生物,合理选择解决方案,并且帮助他们恢复健康。(特别设计缺损的素材“障碍”设置,实现图形思维知识内化迁移与创新)
生:可以!
学生活动:选择合理方案画出设计草图(如图9),进行图形修改制作,让水下城堡恢复往日的生机。
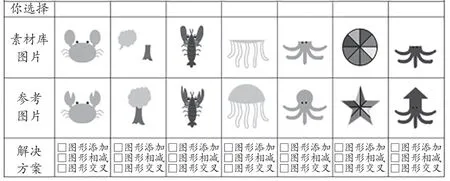
图9
【案例反思】
画图教学中的图形思维养成与应用不同于编程教学,它是通过绘画、设计、创作等活动,在问题解决的过程中形成并显现,因此,画图教学中思维的养成也一定要结合画图教学自身的特点来进行。让图形思维可视,把原本不可视的“图形思维”呈现出来。可视的“图形思维”更有利于学生理解,可以有效提高信息课堂效能。
一、图形问题,步步为营,总结规律
画图模块教学中,“画方形、画曲线、画多边形……”让书本变身“软件说明书”,使教学陷入“基于软件”的怪圈。要提升学生解决问题的能力,教师就要把教学从“基于图形软件教学”转变为“基于图形问题教学”。
(一)课程解读,图形组合
以儿童视角解读问题:利用动画片中的情景——水下城堡遭遇破坏,水王子寻求帮助,发现图形组合运算问题:“需要绘制哪些组合图形?”“如何组合这些图形?”“组合图形的方法有哪些?”从内容本质上解读问题:利用各种形状的不同来组合图形,绘制常规图形不易绘制的形状。
1.图形组合要求一:在研究原始窗户的探究环节中,学生发现8扇窗户,大小规格一致,需要快速绘制相同的8扇窗户。
2.图形组合要求二:在观看Flash动画的过程中,学生发现了月亮形状的宝石,需要快速绘制月牙形状的月亮宝石。
3.图形组合要求三:在观察三张魔法卡片的过程中,学生发现并寻找魔法船,需要利用组合图形快速绘制魔法船。
(二)分析伸展,图形挖掘
发现问题后,教师需要开发和利用教学资源,使用多元的教学策略,帮助学生分析现象,挖掘问题的深层意义。
1.转变局部观念,利用多次选择:学生的原始知识是“从整体到局部”分割大的长方形为小正方形。但均分长方形难度较大。这时,就需要教师引导学生转换思维方式“从局部到整体”,观察发现长方形窗户由8个大小一致的正方形组成。进行多次选择“第1次1个”“第2次2个”“第3次4个”,让学生发现减少复制次数的奥妙——“多次选择”。
2.立体观察方式,形成层间遮挡:在分析“月牙宝石”绘制时,学生的原始知识架构是利用曲线绘制,但发现曲线不够饱满,这时,就需要教师引导学生分析月亮形状,利用Flash动画展示月亮的月相变化,分析出“遮罩层”,让习惯“平面观察”的学生转变观察方式,形成“立体观察”的方式,理解遮挡去除图形局部的效果。
3.图形交叉架构,构建崭新图形:在观察分析三张魔幻卡牌时,突破学生原始的“图形拼接”思考方向,以“图形交叉”这个崭新的思考方式——交叉构图的方式,重新构建了形状的更多可能性。
4.多维图形构图,创新重组思维:引导学生规划个性“水下城堡”,形成个性化设计方案。从形状的来源、形状的组合、形成的图形等环节进行分析,形成多维的图形组合方式,重新构建、创新设计原有构图,并手绘形成设计草图,经小组讨论修改后,经过电脑绘制转变为电子档图片,形成“分析—规划—讨论—绘制—修改”的系列设计过程。
(三)思维导图,图形展现
画图教学常被软件框住思维,课程最后的总结往往是软件操作的方法以及注意事项。而本节课就跨出软件边界,进行了图形思维方式的探讨,从图形组合运算方式总结出“图形添加”“图形减去”“图形交叉”等规律;引导学生感知图形思维,体会图形设计中的逻辑思想;让画图走出软件教学边线,实现图形思维可见。
基础图形思维可见下的课堂,聚焦信息技术综合素养,采用思维导图总结的方式,让整堂课的脉络呈现在学生面前;利用童谣的模式,让课堂要点以文字呈现。思维导图与童谣,展现了课堂思维脉络,真正实现了课堂思维可见。
二、思维提升,层层深入,形成体系
学习与思维水平架构出可视的学习结果结构,不同的五个层次让图形思维水平层次清晰可视(如图10)。一场关于“授之以鱼”还是“授之以渔”的战争,在没有硝烟的信息课堂上打响。如何突破“画图软件”的壁垒,将学生的图形思维从“点、线、面、体”等方面进行提升,需采用以下策略:
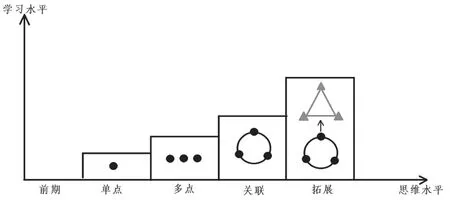
图10
(一)“生活”观察,重塑经验
思维培养还有赖于学生在生活中习得的经验。本节课中涉及的“层”这个概念,通过Flash动画展示月亮的月相变化,展示遮罩效果;用多层透明纸实物道具,绘制图形叠加模仿“层效果”,将生活中常见的透明纸引入课堂,对学生进行经验重组,重塑具象图形思维。
(二)“图形”思维,感悟规律
图形思维与操作思维的不同在于既得的经验不同。教师要引导学生对习得的知识进行分类、归纳、总结,感悟知识规律,形成自己的思考方式,并内化为自己的图形思维模式。就本节课中的图形思维方式来说,从图形数量分为:“单个”与“多个”;从范围分为:“局部到整体”“整体到局部”;从选择方式分为:“单次”与“多次”;从图形组合方式分为:“图形添加”“图形减去”“图形交叉”……仅一节课就有那么多的图形思维方式,学生在课堂上收获的不仅仅是操作技能的掌握,更是习得经验的重组。
(三)“创新”观念,拓展提升
知识的拓展与迁移不是一蹴而就的,而是循序渐进、遵循自身发展规律的。因此,教师要在素材提供上有别常规,设计缺损的素材“障碍”,实现知识迁移与创新。将图形运算的方法与策略进一步内化与提升,更是设计思维与计算思维的碰撞与交融。教路、教法的新颖都不如学生观念的创新,学生在问题解决的过程中逐渐明白组合图形的关系,知识的拓展与迁移有助于学生提升图形思维认知,形成内化的知识体系。
