基于Savonius桨叶的浮式防波堤捕能消波性研究

2022-04-18刘嘉虎刘祚时

水运工程 2022年4期

刘嘉虎，刘祚时，龚凯

(江西理工大学机电工程学院，江西赣州 341000)

浮式防波堤具有抵御破坏力大的深远海波浪、保持内部海域的相对平稳、保护海洋养殖装备、海洋建筑和港口停靠的船只等特点。因其建设成本低、建造周期短，可以针对不同海域进行组合设计等优点使其受到广泛的关注[1]。

Khan等[2]首次将Savonius桨叶(简称“S形桨叶”)用于水轮机水槽试验，结果表明双级转子S形水轮机具有更好的捕能性；Talukdar等[3]通过试验得出S形桨叶水轮机的最优捕能结构参数(双叶片，重叠率 0.15，曲率 1，叶尖速比 0.9)；Huang等[4]设计3个模型，分别对其消波捕能性和系泊力进行对比分析，结果表明S形桨叶与双浮筒浮式防波堤的组合，显著提升了消波性能；邹志利等[5]对作用于浮式防波堤的非线性力进行试验研究，在不同波浪周期、波高、波型和防波堤吃水等参数下进行对比分析；刘崇期等[6]针对具有波浪能转换功能的浮式防波堤性能进行评估，试验表明浮子之间的相互作用是正面的且有助于能量提取；侯勇等[7]改变相对波高、相对堤宽和相对水深等参数对浮式防波堤进行物理模型试验，并将试验数据进行拟合得出计算公式；谢敏捷[8]进行波流耦合状态下S形桨叶性能研究，结果表明波浪的周期与桨叶转动周期满足一定的倍数关系时，桨叶与波浪间存在耦合作用，使桨叶的动转矩系数和功率系数数值大幅提升；鲍灵杰等[9]针对并列与垂直布置的S形桨叶浮式防波堤进行研究，试验表明桨叶并列布置的消波性能比垂直布置更为优越；吴映江等[10]利用数值仿真和试验相结合的方法研究二阶S形桨叶水动力特性，提出一种设置可调开口弹片阀的桨叶，研究重叠率、相对入水深度对桨叶捕能效率的影响。

本文采用双浮筒与二级S形桨叶的组合作为捕能消波一体化装置，在分析其最佳入水深度情况下，通过物理试验与STAR-CCM+软件数值模拟相结合的方法，在不同入射波波高及不同周期的波况下，对该防波堤的捕能性能和消波性能进行分析和对比，其数值模拟结果与物理试验结果得到相互验证。

1 物理试验

1.1 试验模型设置

S形桨叶见图1，模型的主要参数为：叶轮端盘直径Dd=0.40 m，叶轮直径D=0.35 m，叶片直径d=0.20 m，叶片间隙e=0.05 m，高度H=0.60 m。为充分发挥桨叶性能，本文根据测得的理想波况选取大小适中的桨叶，并参考文献[2]和[3]的试验结论，选取重叠率为0.15、曲率为1的双叶片二级S形桨叶进行设计。模型的桨叶采用水平放置，受试验场地限制，桨叶为单排3个，模型整体高度均为1.8 m。

图1 S形桨叶

选择S形桨叶与高密度聚乙烯双浮筒浮式防波堤的组合，在海洋工况下能够耐受各类腐蚀及波浪冲击，实现较长时间的使用寿命。单根浮筒直径0.33 m、长度3 m、质量为40 kg。两根浮筒中心距0.8 m。将S形桨叶悬挂于双浮筒之间，通过调节扁铁可以快速改变入水深度。在桨叶组右侧安装同步轮，通过同步带传送至安装于浮筒右侧的动态扭矩传感器，从而测得实时扭矩以及转速。防波堤三维图见图2。

图2 防波堤三维图

1.2 试验环境设置

试验布置见图3。试验水槽长70 m、宽3.75 m、水深1.8 m。水槽前端配备了摇板式造波机，可产生重复稳定的波形，水槽后端设置方形消波池以减小反射波。防波堤前后各布置2个波高仪用于监测入射波以及透射波波高。锚链系泊采用非交叉系泊式，整体处于平衡位置。

图3 试验布置(单位：m)

1.3 试验参数设置

实际情况中，波浪的状态为瞬时变化，总体呈正态分布，考虑到防波堤难以根据波浪的瞬时变化来不断调节自身最佳入水深度，而试验最终目的是确定该防波堤在特定海域波浪能转化的可行性，因此取理想环境中波浪正态分布的中间区域进行试验，找到最佳波浪状态，设计合适的桨叶尺寸并确定在该波浪状态下的最佳入水深度。1#、2#波高仪分别在造波机不同推板周期和不同推板位移时测得的数据对比见图4(图例中的10、15、20、25 cm指推板位移)。当波浪在波高0.17 m、周期1.6 s时，波形完整、波浪无破碎且波陡合适。分别将桨叶放在该波况的不同入水深度进行测试，对测得的数据进行插值拟合，桨叶入水深度Da与平均转速N的拟合曲线见图5。当Da在0.2～0.3 m时，桨叶单个叶片完全浸入水中，桨叶在整个周期内都能够充分转动，此时模型位于最佳捕能效率区间，得到理想波况下的最佳入水深度为0.26 m。试验共有两组变量，分别为入射波波高Hi分别为0.11、0.14、0.17、0.20 m；周期T分别为1.4、1.6、1.8、2.0 s，将试验模型放置于最佳入水深度，分别在不同波高与不同周期下进行组合测试。

图4 堤前波浪变化对比

图5 模型在不同入水深度的转速

1.4 试验结果分析

模型在不同入射波波高与不同波浪周期条件下的物理试验数据见表1。模型的捕获功率为扭矩与转速的乘积，捕能效率则为捕获功率与波浪功率的比值，捕能效率越高捕能性越好。波浪透射系数是消波性能的重要评价指标，消波波高与入射波波高的比值即为透射系数，透射系数越小，消波性能越好。

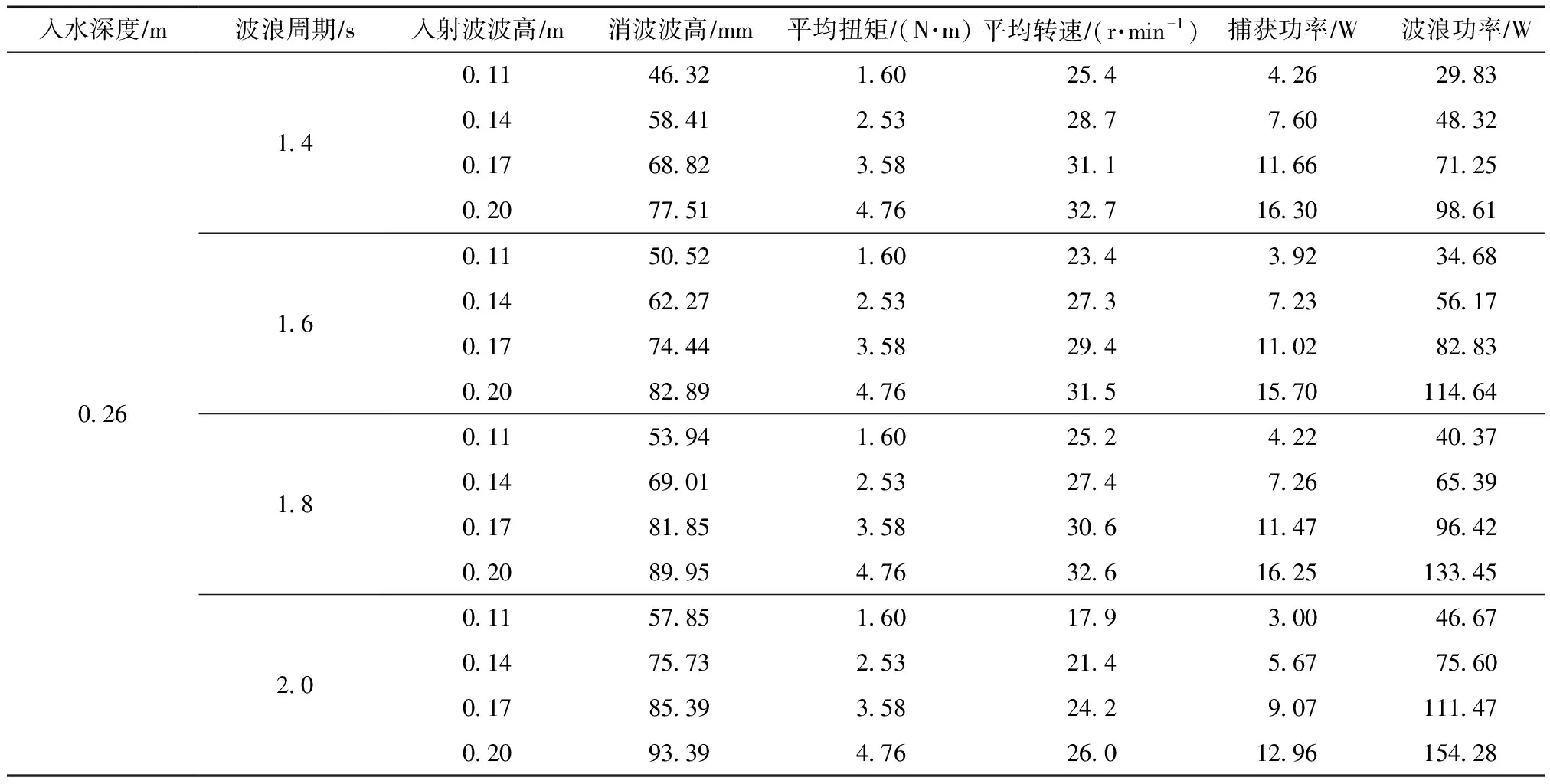
表1 防波堤物理试验数据

1.4.1捕能性能分析

试验模型的捕能效率随不同入射波波高和不同波浪周期的变化见图6。在试验参数范围内，当入射波波高相同时，模型的捕能效率随波浪周期的增大而减小；当波浪周期相同时，模型的捕能效率均随入射波波高的增大而增大。模型在入射波波高0.2 m、波浪周期1.4 s时达到了最大捕能效率16.5%。入射波波高的增加，对捕能效率的提升具有积极作用，但随着波幅不断增大，波浪出现破碎，影响捕能效率。结合表1可知，桨叶在周期为1.4 s时达到了最大平均转速32.7 r/min，尽管桨叶在1.8 s时也达到了理想转速，但此时捕能效率远不及1.4 s周期，而周期为2.0 s时，桨叶平均转速大幅下降，捕能效率也明显下降。

图6 模型捕能效率变化

1.4.2消波性能分析

试验模型的透射系数随不同入射波波高和不同波浪周期的变化见图7。在试验参数范围内，当入射波波高相同时，模型的透射系数随波浪周期的增大而增大，消波性能降低；当波浪周期相同时，模型透射系数的整体趋势随着波高的增加均随波高的增加而下降，消波性能增强，其中在长周期波浪中模型消波性能增强得更加明显。模型的透射系数介于0.39～0.54，模型在入射波波高为0.2 m时，波浪在各个周期内的透射系数均为最低，其中在波浪周期1.4 s时达到了最佳消波效果。

图7 模型透射系数变化

2 数值模拟试验验证

2.1 数值模型及参数

对试验模型重复部分进行简化，在宽度上按照1:3进行缩小，数值模拟水槽设置为长40 m、宽1.25 m、高3 m、水深1.8 m，双浮筒直径为0.33 m、长1 m、浮筒中心距为0.8 m、质量为13.33 kg，浮式防波堤下仅悬挂1个S形桨叶。通过上述比例缩放，在不影响计算精度的前提下，大幅减小计算域，将计算性能合理分配用以后续优化网格以及细化时间步，提升计算精度。

2.2 数值波浪水槽基础设置

基于黏性流体理论，采用STAR-CCM+软件，对规则波进行数值模拟。根据边界造波法原理及阻尼消波原理，建立S形桨叶浮式防波堤的三维数值模型，采用湍流模型、重叠网格技术、六自由度运动模型、VOF(volume of fluid，流体体积)自由液面捕捉技术在计算域内进行气液两相流计算透射系数等参数，并监测桨叶捕能性能。

沿坐标系3个方向的动量守恒定理为：

(1)

(2)

(3)

式中：ρ为流体的密度；t为时间；p为流体压强；μ为黏度；u、v、w为沿x、y、z方向的速度分量；Su、Sv、Sw为边界条件。

RNG(renormalization group，重整化群)湍流模型，通过添加ε方程考虑涡流对湍流的影响，提升了高速流动的计算准确性[11]，方程如下：

(4)

在进行CFD(computational fluid dynamics，计算流体动力学)仿真时，运动学的边界条件一般为：

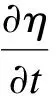
(5)

Z=η(x，y，t)

(6)

流体体积(volume of fluid，VOF)法通过在整个计算流体域中引入了一个函数ψ，表示为水相或气相的体积占计算域网格单元体积的比值，可以实现聚类变化下的波面捕捉，大幅提高数值模拟的计算精度[12]。这种方式用公式表示为：

(7)

(8)

式中：ψp为计算域单元网格中p相流体的体积分数；ρp为计算域中p相流体的密度；vp为计算域中p相流体的速度矢量。

2.3 有限元模型

在流域相对不重要区域适当增大网格，在与模型接触的交界面上细化网格，用于捕捉交界面上流体的剧烈变化。同样需要在波面附近进行网格细化，用以捕捉波面的变化，观察防波堤模型的消波效果。防波堤加密网格及桨叶边界过渡层加密网格见图8。

图8 加密网格

在STAR-CCM+软件中利用DFBI(dynamic fluid body interaction，流体与刚体相互作用)功能，防波堤开放3个自由度：沿x、z轴的移动和绕y轴的转动。将S形桨叶和防波提做耦合，实现与防波堤同步运动，并为S形桨叶开放一个绕y轴旋转的自由度，即桨叶能在波浪的作用下旋转。多项流分离见图9，防波堤渲染图见图10。

图10 防波堤渲染图

2.4 数值模拟结果及对比

模型在不同入射波波高与不同波浪周期条件下的数值模拟数据及对比见表2，数值模拟与物理试验的捕能效率、透射系数对比见图11。可以看出，平均转速的模拟值和捕获功率的模拟值略大于试验值，原因在于试验的装配误差，3个二级桨叶在装配中不能保持很高的同轴度，在旋转过程中增加了阻力，使得在波浪的冲击下物理试验的平均转速不及模拟值，在转速得到提升的同时，捕能效率的模拟值也略微大于试验值。消波波高的模拟值略小于试验值，原因在于数值波浪水槽在正常传播的过程中存在波浪衰减，堤后测量位置相较于产生波浪的速度入口距离较远，波浪衰减也更加明显，使模型数值模拟的消波性能略优于物理试验的消波性能。模拟值与试验值的变化趋势基本一致，且对比差异均在误差允许的范围内。