硬脆性材料用柔性磨具研磨的加工表面粗糙度建模
2022-04-18章玉强胡中伟朱泽朋崔长彩陈铭欣谢斌晖李瑞萍
章玉强 胡中伟 朱泽朋 崔长彩 陈铭欣 谢斌晖 李瑞萍
1.华侨大学制造工程研究院,厦门,3610212.脆性材料产品智能制造国家地方联合工程中心,厦门,3610213.福建晶安光电有限公司,泉州,362411
0 引言
蓝宝石、单晶碳化硅、陶瓷、石材等硬脆性材料因具有良好的力学、物理和光学性能而被广泛应用于光电衬底、光学窗口及高温高强结构元件等众多军用及民用设备[1-3]。这些硬脆性材料产品在应用中均需经过精密和超精密加工,以获得较高的形状精度和表面质量,然而,高硬度和高脆性使在其加工过程中很容易产生表面破碎和裂纹等缺陷,严重影响零件的表面质量和使用性能[4]。以橡胶和有机高分子为结合剂的柔性磨具具有良好的弹性,加工过程中,当磨具表面磨粒受力较大时,结合剂能产生一定的弹性变形,磨粒形成退让,使磨粒出露高度变得较为一致,有效避免了少数凸出磨粒因压力过大而产生较深的划痕或裂纹,降低了工件的表面粗糙度,提高了表面质量,因此,柔性结合剂磨具在加工硬脆性材料方面具有明显的优势,已成为硬脆性材料精密加工的一种重要材料。粗糙度是评价加工表面质量的一个重要参数。硬脆性材料研磨的过程中,材料硬度高、脆性大的特点,以及磨具表面磨粒的多样性,使得对其加工表面粗糙度的控制及预测较为困难,因此,有必要建立硬脆性材料柔性磨具加工表面粗糙度预测模型,以便更好地揭示柔性磨具加工机理、优化加工工艺,提高加工表面质量。
目前已有大量学者针对回归分析法、理论推导法和人工智能法等各类磨具加工的表面粗糙度预测建模方法进行了研究[5]。回归分析法在大量实验数据基础上,利用数理统计方法进行回归分析,建立自变量与因变量之间的函数表达式[6]。甄婷婷等[7]对大量实验数据进行指数回归分析,建立了C/SiC复合材料平面磨削的粗糙度模型。TIAN等[8]利用多元非线性回归理论分析了工程陶瓷表面纹理特征与其表面粗糙度的关系。JOSHI等[9]基于机器视觉参数回归模型,通过多元回归分析,建立了表面粗糙度与基于灰度共生特征的主成分之间的关系模型。理论推导方法基于磨粒与工件表面的相互作用关系及表面形貌形成机理来建立表面粗糙度模型,即将加工工艺参数代入理论模型来计算表面粗糙度。SHAO等[10]基于砂轮表面磨粒随机分布状态及磨粒出刃高度满足瑞利分布的条件,建立了陶瓷磨削的表面粗糙度预测模型。WU等[11]认为磨粒的磨削深度服从瑞利分布,并考虑接触刚度推导了碳化硅磨削的表面粗糙度预测模型。WU等[12]建立了考虑材料韧性和脆性去除机理、晶粒突出条件、材料性能和加工参数的表面粗糙度模型,并进行了氧化铝和单晶硅的磨削实验,实验结果表明粗糙度实验值与理论值的平均误差为15%。人工智能法是将计算机遗传算法和神经网络算法等技术用于表面粗糙度的建模,用来预测加工零件的表面粗糙度。NGUYEN等[13]提出一种在线预测砂轮表面粗糙度模型,该模型基于自适应神经模糊推理系统-高斯过程回归和田口分析的混合算法,用于在线监测钛合金磨削的表面粗糙度和砂轮磨损,实验结果表明该模型精度较高,其平均误差为0.31%。GOPAN等[14]通过将人工神经网络与遗传算法集成,开发了磨削预测和优化模型,试验证明该方法在磨削参数影响预测和优化应用中是可行的。SIZEMORE等[15]基于机器学习和人工神经网络模型对单晶金刚石车削加工过程中的表面粗糙度进行预测,发现预测结果与实验结果误差较小。上述学者采用不同方法建立的各类磨具加工表面粗糙度预测模型对指导磨具设计和工艺优化具有重要意义。
由于柔性磨具加工中磨粒的退让作用,现有固结磨料研磨表面粗糙度的预测模型难以适用于硬脆性材料柔性磨具加工表面粗糙度的预测。因此,笔者通过对柔性磨具加工过程中磨粒与工件的相互作用过程进行分析,并基于磨粒受力平衡原理,计算磨粒切深与结合剂变形,建立柔性磨具加工表面粗糙度的理论预测模型。以橡胶结合剂研磨盘为柔性磨具、蓝宝石衬底为工件,在不同弹性模量、磨粒浓度、磨粒粒度和研磨压力下开展研磨试验,验证表面粗糙度模型的可靠性。
1 建模过程
固结磨料加工过程中,磨粒分布、有效磨粒数和磨粒出露高度是影响加工表面粗糙度的关键。实际研磨过程中,磨具表面的磨粒是随机分布的,大小、形状存在一定的差异,且磨粒的出露高度也存在一定的差异,导致每个磨粒产生的划痕不同,这都将使建模过程变得复杂且困难[16]。因此,为便于分析,在建模过程中需进行一些合理的简化和假设:
(1)磨粒的粒径均匀,形状均为八面体,并以四棱锥的形状切入工件[17]。
(2)磨粒切削工件表面产生的沟槽剖面形状与磨粒的锥顶角及磨粒切削深度所构成的三角形相对应,沟槽大小由切屑厚度决定[18]。
(3)表面粗糙度模建模只考虑单颗磨粒的作用,不考虑轨迹重叠对表面粗糙度的影响[19]。
1.1 有效磨粒数及磨粒出露高度测量
为测量磨具表面有效磨粒数及磨粒的出露高度,首先采用不同配方制备一批不同磨粒粒径、不同磨粒浓度,以及不同弹性模量的橡胶结合剂磨块,然后对磨块表面的磨粒分布及磨粒出露高度进行测量。
1.1.1有效磨粒数的测量
采用KH-8700三维视频显微镜对磨块表面磨粒分布进行观测,测量单位面积内的磨粒间距和磨粒数,计算磨块表面磨粒的密度分布。根据研磨盘与工件表面接触的有效面积,计算出研磨盘表面磨粒与工件表面接触的有效磨粒数。
测试过程中,每种配方磨块挑选10个样品进行观测,每个样品表面选取5个0.5 mm×0.5 mm的区域进行测量,如图1所示,测量相邻磨粒间距li(i=1,2,…,5)和该区域内的磨粒数量N,通过测量的磨粒数与面积计算磨粒密度分布。最后将10个样品的磨粒密度分布平均值作为该配方研磨盘表面磨粒的密度分布。表1所示为磨粒浓度200%、磨粒粒度230/270、弹性模量23.87 MPa的10个橡胶结合剂研磨盘的磨粒分布密度。

图1 磨粒分布情况
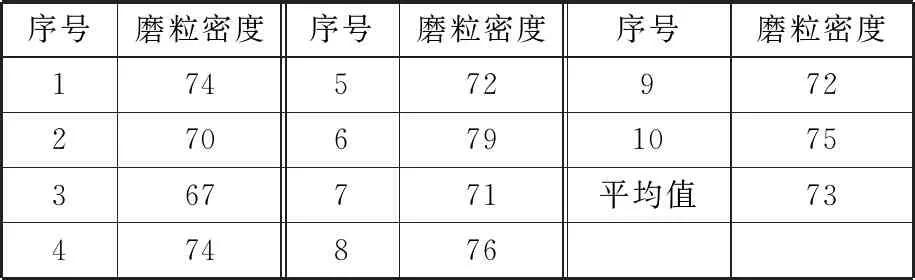
表1 磨粒分布密度
为计算有效磨粒数,需计算工件与研磨盘表面的有效接触面积。选取直径300 mm的橡胶研磨盘为实验用柔性磨具、直径100 mm(4英寸)蓝宝石衬底为工件。研磨盘与工件表面的有效接触面积如图2阴影部分所示。根据磨盘冷却液流道宽度(2 mm)算出工件覆盖的冷却液流道面积(1778 mm2)。工件面积减去冷却液流道面积即工件与研磨盘表面的有效接触面积。有效接触面积与磨粒分布密度的乘积即有效磨粒数。
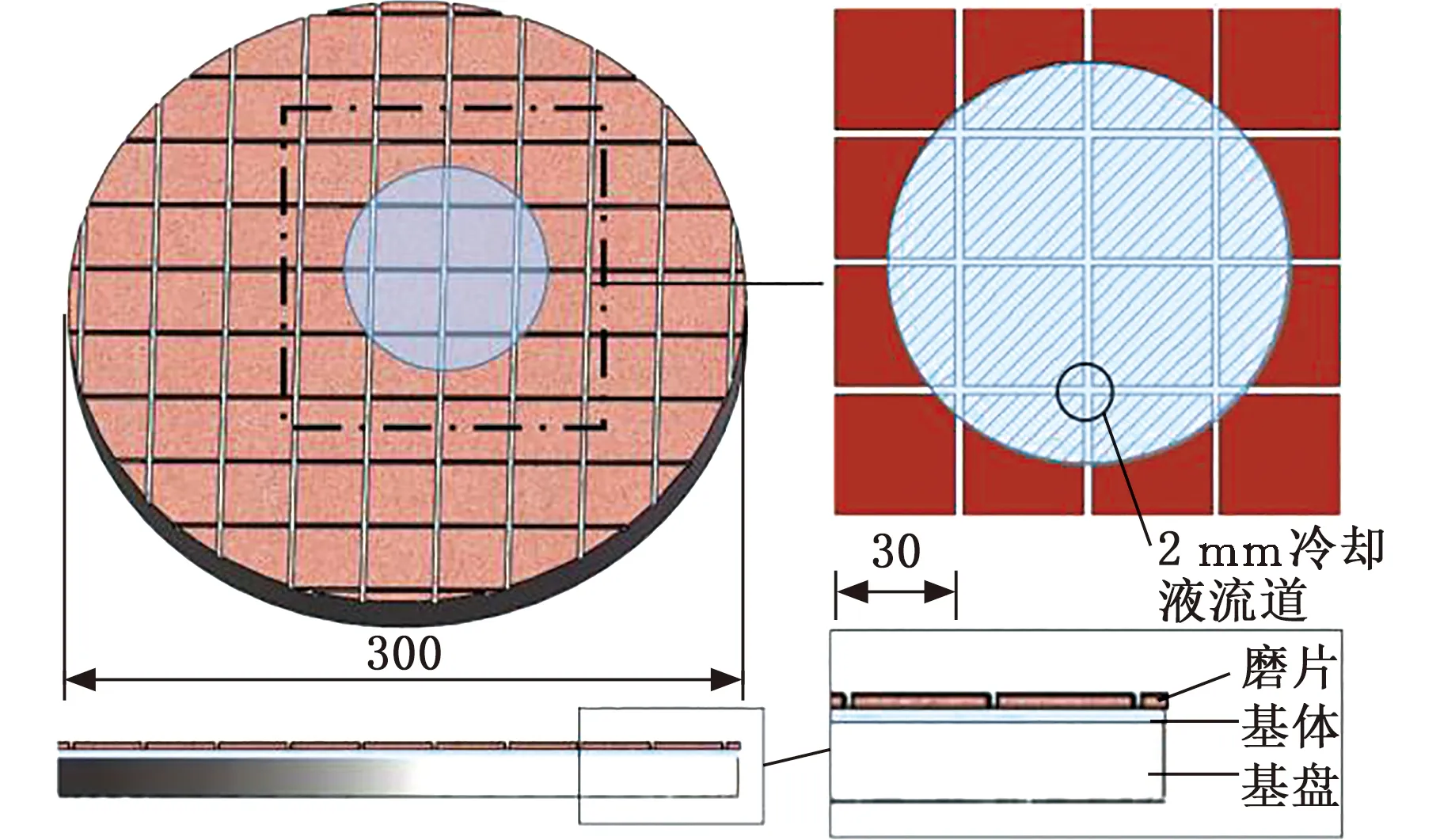
图2 研磨盘及有效加工区域
1.1.2磨粒出露高度的测量
由于磨具表面磨粒的出露高度不同,而研磨过程中不同出露高度磨粒对工件表面的作用效果也不同,因此,需对磨具表面磨粒的出露高度进行测量并分组,计算不同出露高度磨粒所占的比例,以分析不同出露高度的磨粒对加工表面粗糙度的影响。首先采用KH-8700三维视频显微镜对磨具表面磨粒的出露高度进行测量,如图3所示。然后对一定数量磨粒的出露高度测量值进行统计分析,图4为所测量107颗磨粒的出露高度分布图,最大出露高度为23 μm,但大部分磨粒出露高度为5~15 μm。
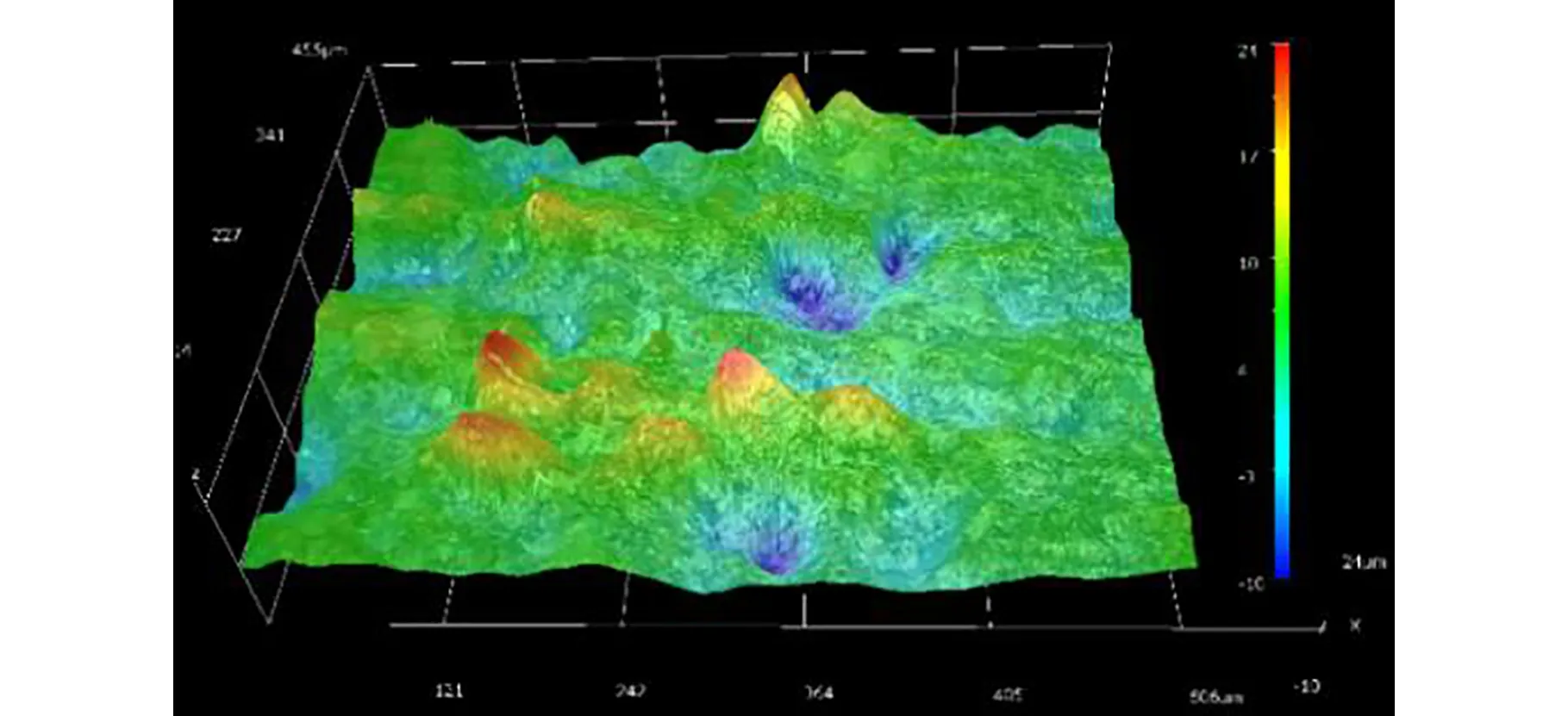
图3 磨粒的出露高度

图4 磨粒出露高度统计
磨粒出露高度的随机分布可根据YOUNIS等[20]提出的瑞利分布函数描述:
(1)
其中,h为磨粒出露高度;β为完全定义瑞利概率分布函数的参数,取决于研磨条件和研磨盘的微观结构及工件材料。图4所示的磨粒出露高度拟合曲线符合瑞利分布,上述瑞利分布函数的期望值E(h)和标准偏差SD(h)分别为
(2)
(3)
为便于分析,根据不同的出露高度对磨粒进行等级划分,等级划分跨度大会减小计算量,但是计算精度低、误差大,等级划分跨度小时,计算精度高、误差小,但是计算量大。综合考虑,本实验中划分了五个等级,每5 μm取一个等级,并取每一等级磨粒出露高度的平均值作为该等级磨粒的出露高度,再根据瑞利分布函数计算不同高度的磨粒在有效磨接触区域内参与研磨的占比,如表2所示。

表2 磨粒出露高度等级及占比
1.2 磨粒与工件作用过程分析
研磨过程中磨粒的受力如图5所示,磨粒在法向受到工件下压力F1和橡胶结合剂对磨粒的支持力F2。在下压力F1的作用下,磨粒切入到工件,实现对工件材料的去除。磨粒切入工件深度与下压力F1的关系为[21]
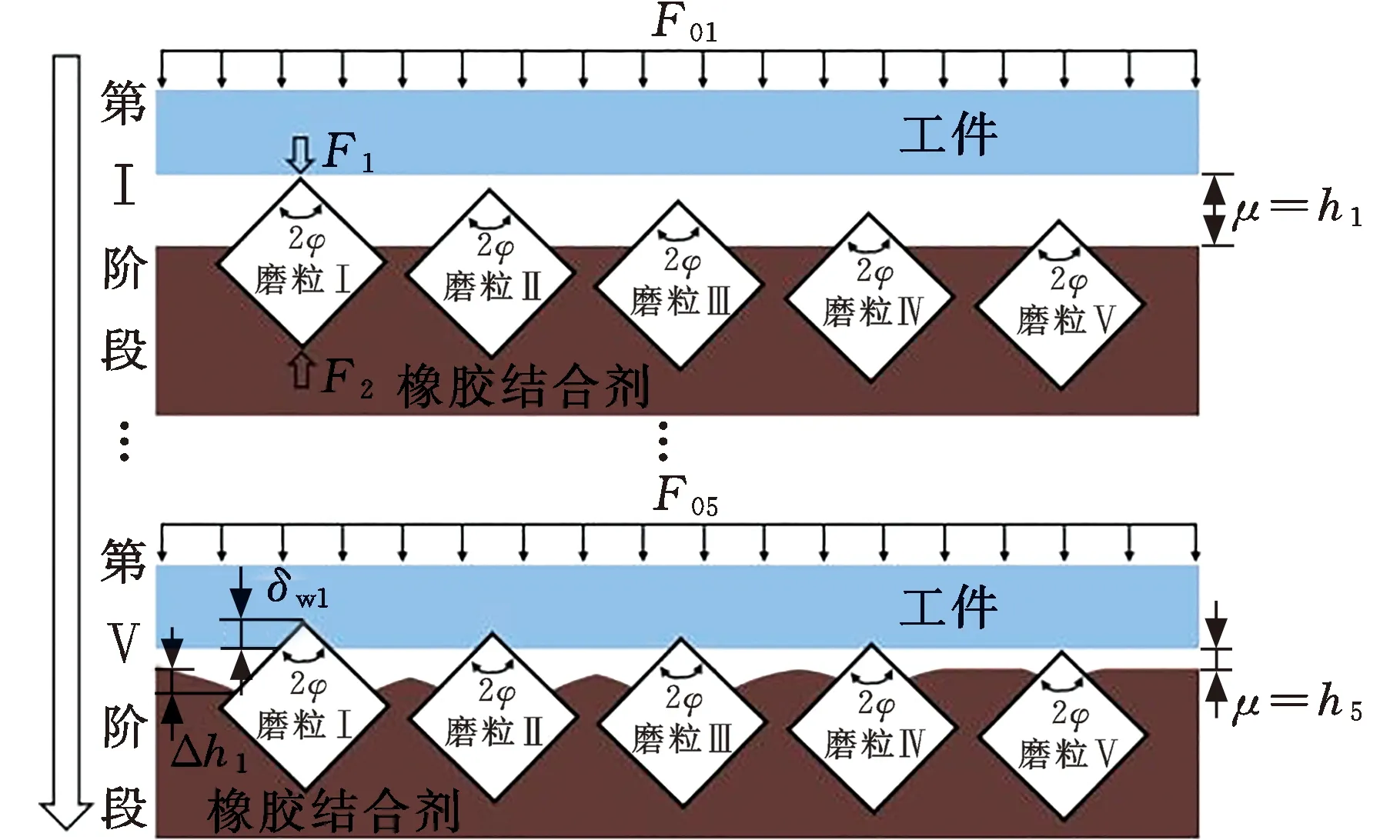
图5 金刚石磨粒受力示意图
(4)
式中,Hα为工件(蓝宝石)的硬度,Hα=19.88 GPa;φ为金刚石磨粒的锥顶角;δw为磨粒切入工件的深度。
由于下压力F1的作用,磨粒会在法向产生退让,橡胶结合剂产生弹性变形,同时结合剂对磨粒提供支持力F2。磨粒退让深度与支持力F2的关系为[22]
(5)
式中,D为磨粒粒径;E为橡胶结合剂磨具的弹性模量;Δh为磨粒退让的深度。
加工过程中,金刚石磨粒在法向处于平衡状态,因此根据力的平衡条件可得
(6)
柔性磨具研磨过程中,随着研磨下压力的增大,磨盘表面参与加工的磨粒逐渐增多。研磨下压力较小时,只有出露高度较大的第1等级磨粒参与加工;研磨下压力增大时,除第1等级的磨粒参与加工外,出露高度稍小的第2等级磨粒也参与加工。依此类推,只有当研磨下压力达到一定程度时,出露高度较小的第5等级磨粒也参与加工。因此,可根据不同出露高度磨粒参与加工情况将研磨过程分为5个阶段。随着加工下压力的增大,参与研磨加工的磨粒增多。工件与结合剂平面的距离μ=h1时,第1等级磨粒开始参与研磨。随着加工下压力的增大,工件与结合剂平面的距离减小,即当μ=h2,h3,h4,h5时,第2~5等级磨粒继而开始参与研磨。在不同加工阶段,磨粒初始出露高度与退让量、切深之间的关系为
h=μ+δw+Δh
(7)
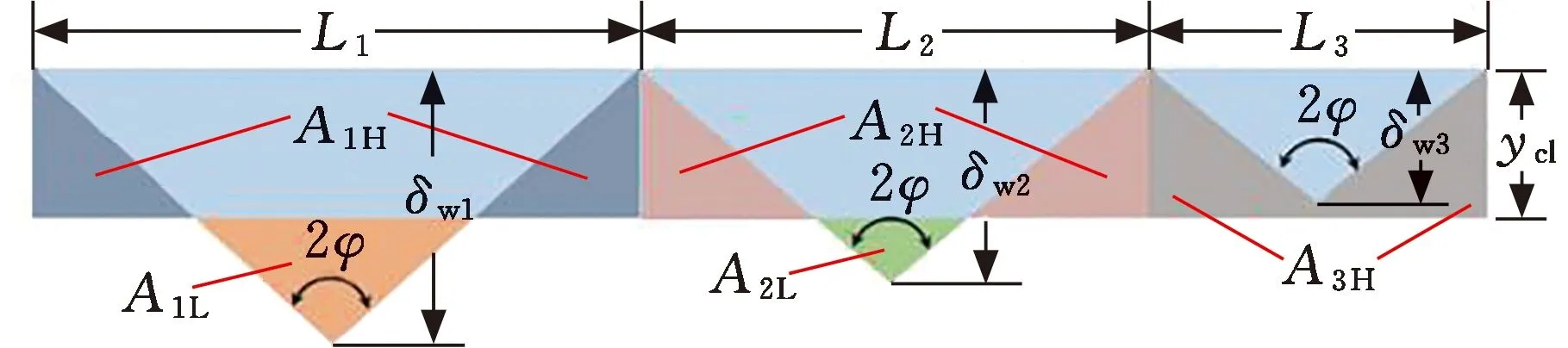
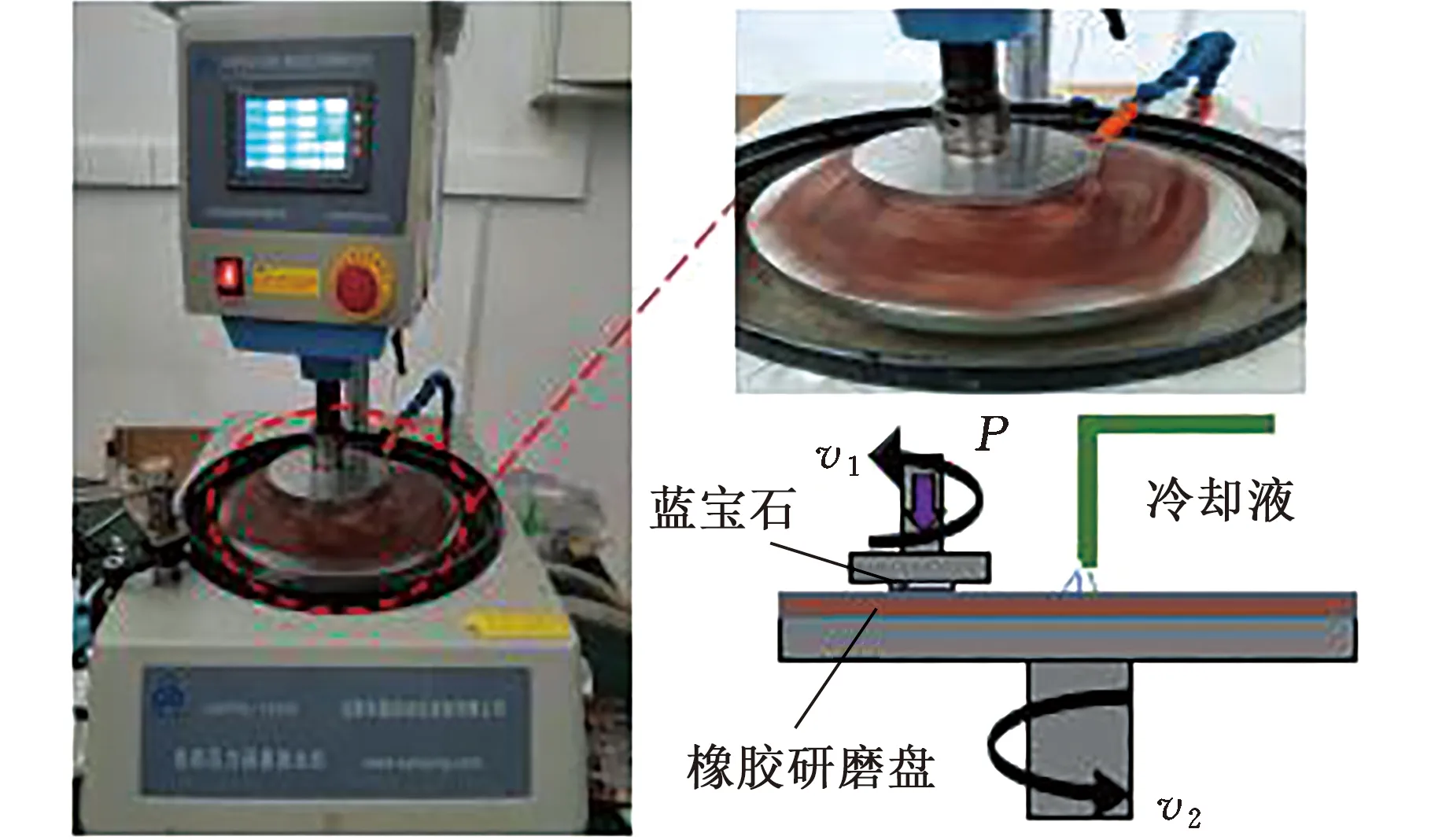
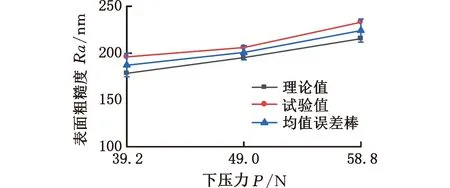
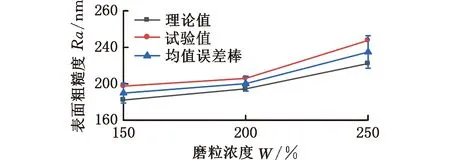
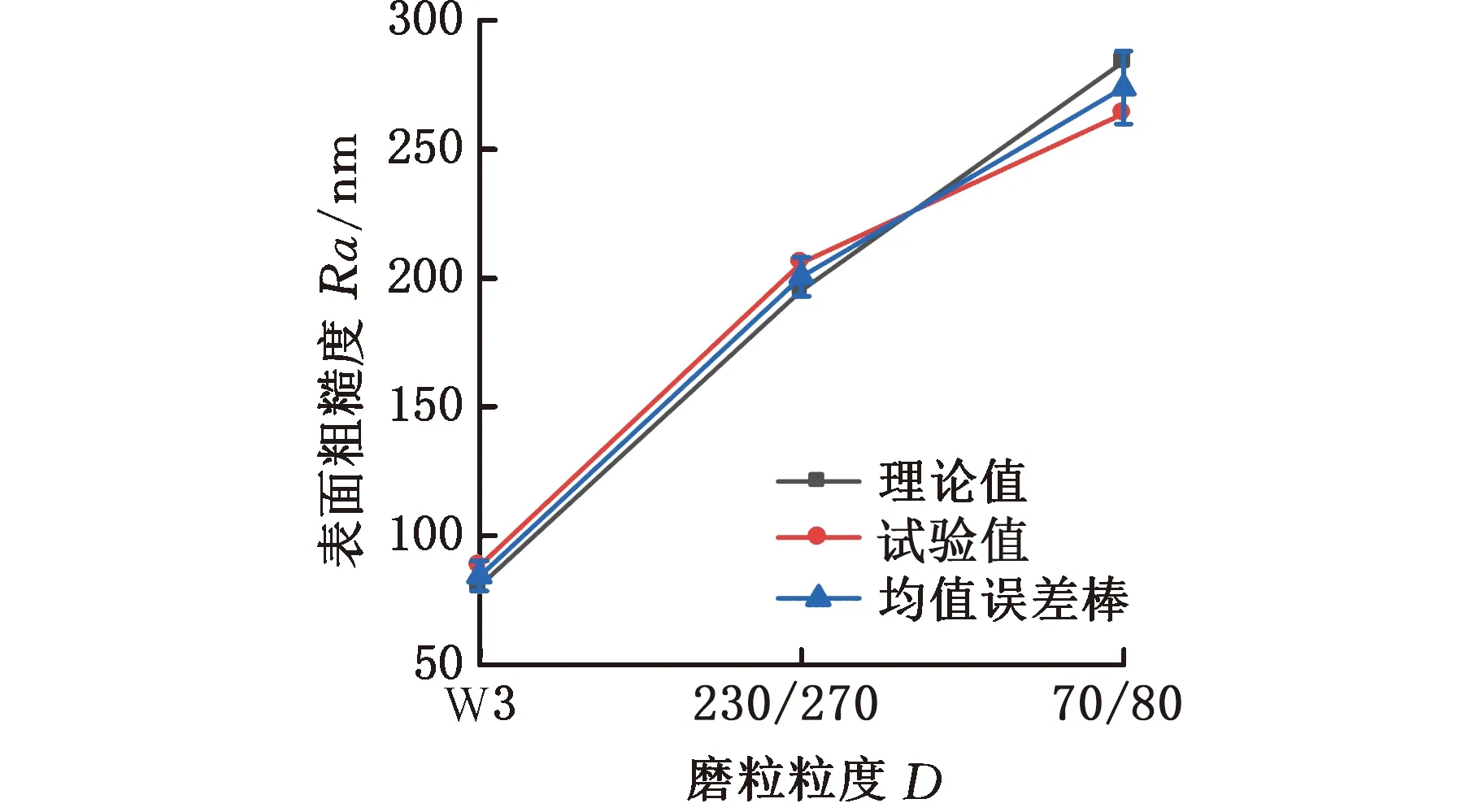
(1)当加工下压力0 F01=F11f(h1)N (8) 式中,F11为出露高度为h1的单颗磨粒从阶段1向阶段2过渡时的临界下压力;f(hi)为等级i的磨粒在有效接触区域内参与研磨的理论占比,i=1,2,…。 由式(4)、式(8)可得第1阶段磨粒的切深 (9) (2)研磨下压力F01≤F F02=F12f(h1)N+F22f(h2)N (10) 其中,F12、F22分别是出露高度为h1和h2的单颗磨粒从阶段2向阶段3过渡时的临界下压力。 根据式(6)、式(7)可得出第1组和第2组磨粒切深之间的关系: (11) 为了便于计算,对公式进行简化,代入具体数值,使用Origin软件画出式(11)的函数曲线图(图6),并对其进行拟合,可近似得到两组磨粒切深δw1和δw2之间的关系: 图6 磨粒切深拟合曲线 (12) 由式(4)、式(10)、式(12)可得加工下压力F与磨粒切深δw1和δw2之间的关系: (13) 研磨下压力继续增大时,下压力与磨粒切深、磨粒退让深度的关系可依此类推。 本文选用轮廓算术平均偏差Ra作为研磨表面粗糙度的评定指标[19]: (14) 研磨过程中,不同出露高度磨粒在工件表面产生的划痕深度不同,导致工件表面沟槽轮廓截面形状的大小也不相同,如图7所示,图中,ycl为基准线到工件表面的距离,Li为不同出露高度磨粒在工件表面划痕的取样长度,δwi为不同出露高度磨粒产生的切深,AiH为深度大于基准线的划痕所产生的面积,AiL为深度小于基准线的划痕所产生的面积。 图7 工件表面沟槽轮廓截面形状示意图 由粗糙度算术平均偏差的基准线定义可知,基准线上下部分的面积相等[23],即 aA1H+bA2H+…+nAiH=aA1L+bA2L+…+nAiL (15) 式中,a,b,…,n为不同出露高度的磨粒在有效接触区域内参与研磨的占比。 以研磨下压力0 (1)加工下压力0 (16) (2)当加工下压力F1≤F (17) 由此联立式(13)、式(17)可得到表面粗糙度Ra与加工下压力F之间的关系。当下压力继续增大时,表面粗糙度Ra与加工下压力F之间的关系可依此类推。 为验证硬脆性材料柔性磨具加工表面粗糙度预测模型的正确性,选用不同弹性模量、磨粒浓度、磨粒粒度的橡胶研磨盘,在不同研磨下压力下进行4组研磨试验。研磨试验在UNIPOL-1200S研磨机上进行,其加工原理如图8所示,研磨试验工艺参数如表3所示。 表3 研磨试验参数 图8 研磨机及其加工原理示意图 研磨后的蓝宝石衬底分别采用无水乙醇和去离子水进行超声清洗,然后采用Zygo NV700 3D光学轮廓仪对衬底表面粗糙度进行测量。每次测量中心和四周共5个点,并以5个点的粗糙度平均值作为该工件的表面粗糙度。 每组试验在相同条件下重复3次,取表面粗糙度平均值作为该试验条件下研磨蓝宝石衬底获得的试验值。将表3所示的试验研磨工艺参数值代入式(16)、式(17)获得表面粗糙度的理论值后,再将试验结果与理论计算结果进行比较分析。 采用结合剂弹性模量23.87 MPa、磨粒粒度230/270、浓度200%的橡胶结合剂金刚石研磨盘,在研磨盘转速120 r/min,研磨下压力分别为39.2 N、49.0 N和58.8 N条件下对蓝宝石衬底进行研磨试验。不同下压力下研磨蓝宝石衬底测得的表面粗糙度如图9所示。随着研磨下压力的增大,表面粗糙度增大。不同研磨下压力下的表面粗糙度试验值与理论值的变化趋势一致,且误差在5.51%~9.89%以内。随着下压力的增大,磨粒嵌入工件表面深度增大,工件表面形成的沟槽更深,表面粗糙度增大。实际研磨中,研磨下压力较小时,只有出露较高的磨粒参与研磨,表面粗糙度试验值相对于理论值偏差较大。随着下压力逐渐增大,参与研磨的磨粒逐渐增多,研磨均匀性变好,表面粗糙度试验值相对于理论值偏差逐渐变小。粗糙度的理论模型未考虑磨粒断裂磨损和脱落等因素对研磨过程的影响。研磨下压力继续增大时,磨粒更容易发生断裂和脱落,断裂和脱落的磨粒硬度较大,在研磨过程中容易对工件表面造成表面划伤、破碎等损伤,造成表面粗糙度变大。因此,表面粗糙度的试验值与理论值相对偏差又逐渐增大。 图9 下压力与表面粗糙度关系 在研磨转速120 r/min、研磨下压力49 N下,采用不同弹性模量(19.19 MPa、23.87 MPa和39.59 MPa)结合剂的金刚石橡胶研磨盘(磨粒粒度230/270、浓度200%)加工蓝宝石衬底,其表面粗糙度如图10所示。随着研磨盘结合剂弹性模量的增大,研磨表面粗糙度增大。不同弹性模量下,表面粗糙度试验值与理论值的变化趋势一致,且误差在8.57%~12.55%内。表面粗糙度试验值与理论值的相对偏差随磨具弹性模量的增大逐渐变大。随着磨具弹性模量的增大,磨具的硬度增大,磨粒更容易切入工件表面,导致研磨切屑厚度变大、表面粗糙度增大。试验过程中,研磨盘的弹性模量增大时,磨具的硬度增大,则相同下压力下的磨具变形减小,磨粒的退让效果变差,使得磨粒实际切入工件的深度大于理论深度。另一方面,磨具弹性模量较大时,只有出露高度大的磨粒参与研磨会导致研磨均匀性较差、工件表面产生深凹槽,造成表面粗糙度变大。因此,当磨具的弹性模量较大时,理论值与试验值的相对误差较大。 图10 磨盘弹性模量与表面粗糙度关系 在研磨转速120 r/min、研磨下压力49 N下,采用不同磨粒浓度(100%、200%和300%)的金刚石橡胶研磨盘(结合剂弹性模量23.87 MPa、磨粒粒度230/270)加工蓝宝石衬底,不同磨粒浓度的研磨盘加工表面粗糙度如图11所示。随着研磨盘磨粒浓度的增大,研磨表面粗糙度增大。不同磨粒浓度下,表面粗糙度试验值与理论值的变化趋势一致,且误差在5.94%~11.42%内,但表面粗糙度试验值与理论值的相对偏差随磨粒浓度的增大逐渐变大。随着磨粒浓度增大,磨粒间距不断减小,磨粒密度增大,这导致磨粒间的摩擦作用在混料过程中增强,不利于磨粒均匀分布在橡胶中;另一方面,磨粒浓度增大导致磨具的弹性模量增大,进而导致工件表面粗糙度增大。磨粒浓度较高导致结合剂对磨粒的把持效果相对变弱,磨粒更容易脱落。脱落的磨粒会造成蓝宝石表面划痕,增大表面粗糙度。因此,磨粒浓度较高时,理论值与试验值的相对误差较大。 图11 磨粒浓度与表面粗糙度关系 在研磨转速120 r/min、研磨下压力49 N下,采用不同磨粒粒度(W3、230/270和70/80)的金刚石橡胶研磨盘(结合剂弹性模量23.87 MPa、磨粒浓度200%)加工蓝宝石衬底,不同磨粒粒度的研磨盘加工表面粗糙度如图12所示。随着研磨盘磨粒粒度的增大,研磨表面粗糙度增大。不同磨粒粒度下的表面粗糙度试验值与理论值的变化趋势一致,且误差在5.46%~10.13%内。表面粗糙度试验值与理论值的相对偏差随磨粒粒度的增大逐渐变大。随着磨粒粒度的增大,磨粒间距不断变大,间距波动变大,磨粒的分布密度变小,分布均匀性变差,导致工件表面粗糙度增大。磨料浓度相同的情况下,粒度小的磨粒相对较少。混料过程中,磨料的分布具有一定的随机性,根据概率学理论,磨粒越多,随机分布越均匀。试验过程中,同一组磨粒的粒径偏差较大,进而将磨粒粒径的平均值代入公式后计算的理论值会偏大,造成理论值偏大。因此,磨粒粒度较大时,理论值比试验值大,且相对偏差较大。 图12 磨粒粒度与表面粗糙度关系 不同条件下研磨试验所得表面粗糙度的试验结果与理论模型的预测结果相吻合,验证了所建立的表面粗糙度预测模型的正确性,但由于理论模型未考虑磨屑、冷却液、磨盘振动、磨粒粒径差异、磨粒磨损脱落和研磨轨迹重叠等因素的影响,故模型仍存在一定误差。 (1)通过分析柔性磨具加工过程中磨粒与工件的相互作用过程,并基于磨粒受力平衡原理,计算了磨粒切深与结合剂变形,建立了柔性磨具加工硬脆性材料的表面粗糙度理论预测模型。 (2)通过研磨试验发现不同条件下的研磨表面粗糙度试验值与理论值变化趋势一致,且预测平均误差在7.71%~10.1%内,验证了所建立的硬脆性材料柔性磨具加工表面粗糙度理论模型的可靠性。 (3)通过建立硬脆性材料柔性磨具加工表面粗糙度理论模型,可以有效预测不同条件下加工工件表面粗糙度,这有利于优化加工工艺参数,提高加工表面质量,降低加工成本。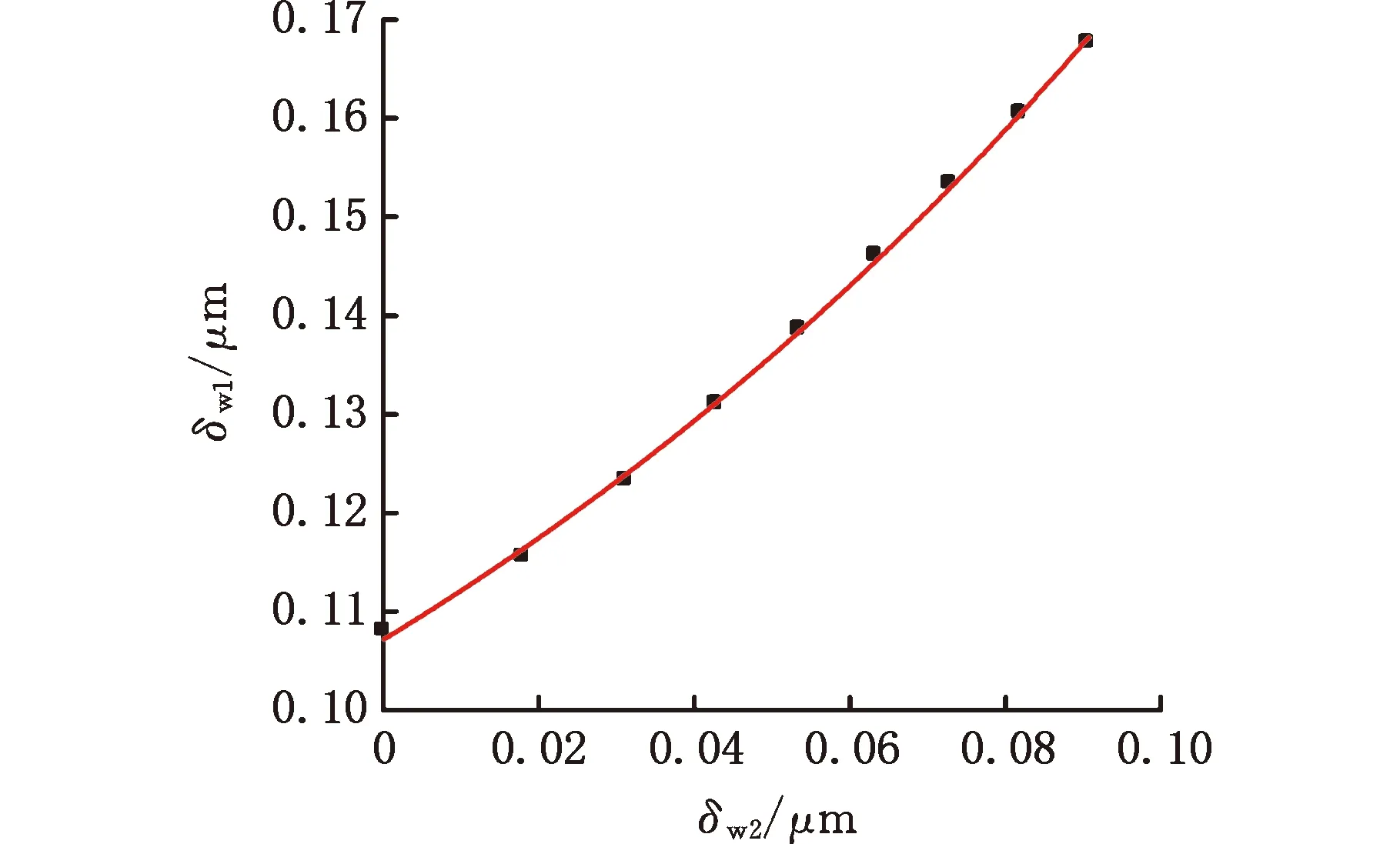
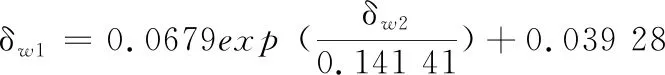
1.3 表面粗糙度模型的建立
2 验证试验

3 理论值与试验值的比较分析
3.1 不同下压力下的表面粗糙度
3.2 不同弹性模量下的表面粗糙度

3.3 不同磨粒浓度下的表面粗糙度
3.4 不同磨粒粒度下的表面粗糙度
4 结论
