查看日历估算地球轨道偏心率

赵诗华 朱 琴 蔡亚璇

（1.中国矿业大学（北京）理学院，北京 100083；2.北京市昌平区第二中学，北京 102208）

翻开日历即可看到2021年9月23日是秋分，3月20日是春分，而2020年的秋分是9月22日.当然，24节气一般都可以在日历中查到.但是春分、秋分的时间却可以用来推算地球公转轨道的偏心率.

开普勒第一定律［1］告诉我们，地球公转轨道是椭圆，太阳位于椭圆的一个焦点上，设椭圆的半长轴为a，半短轴为b，半焦距为c，如图1所示.众所周知，太阳在秋分、春分之日直射赤道，如图1中A、B两点所示；在冬至、夏至分别直射南北回归线，如图1中P、Q两点所示.

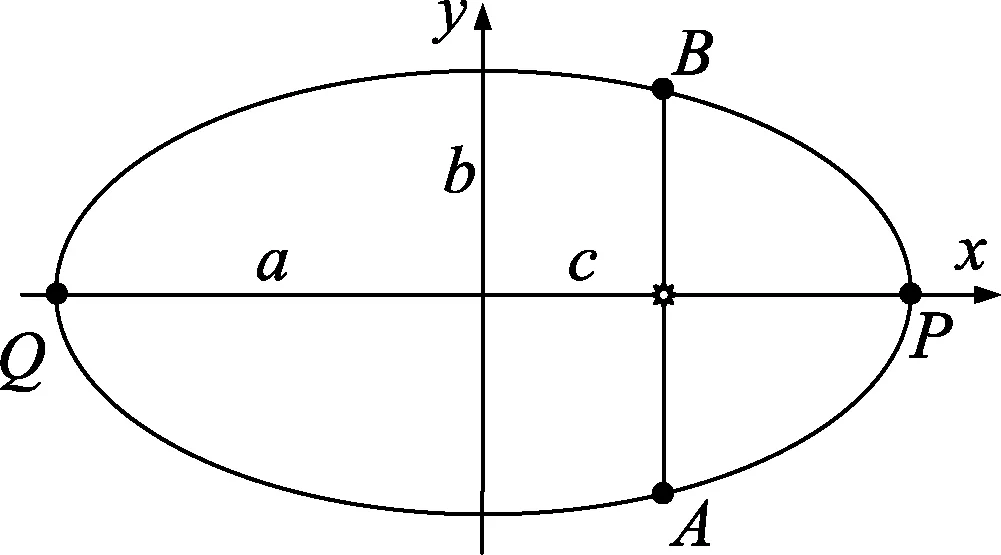
图1 地球公转轨道示意图

由图1、图2可知，矩形A′B′C′D′的边长分别为2b和2c，椭圆面积为S=πab，代入（3）式得到

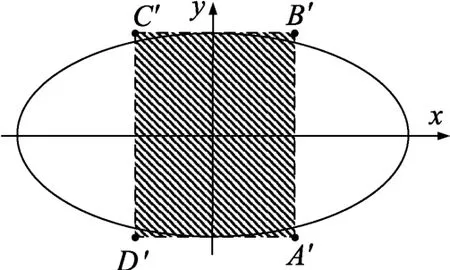
图2 ΔS的矩形近似

从而推得地球公转轨道的偏心率e为

如果将地球的公转周期T近似为365天，由2020年的9月22日至2021年3月20日的时长取为T1，2021年3月20日至2021年的9月23日取为T2，可得ΔT=8天，代入（5）式有

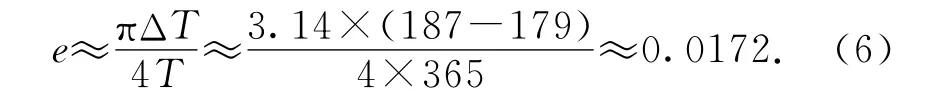
地球轨道偏心率的真实值为

从而（6）式的相对误差为

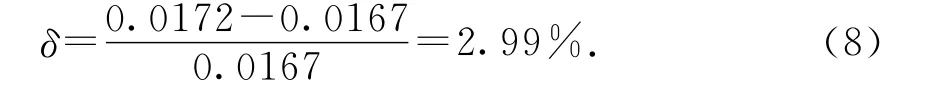
由此可见，用日历估算地球轨道偏心率的方法是可取的.

当然，由于春分、秋分的日期并非完全固定，除了ΔT=8天之外，还会出现ΔT=7天的情形，此时的结果为e≈0.0151.由于4年为一个闰年周期，考察连续4年的情况就会发现，e≈0.0172和e≈0.0151出现的次数是相等的.以2017年春分至2021年秋分这一时间段为例，春分→秋分→春分之间的时间间隔为187天→179天→186天→179天→186天→178天→186天→179天→187天.按照上述方法计算，e≈0.0172和e≈0.0151各两次，取偏心率的平均值就得到

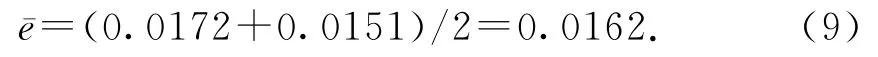
相对误差仍然为3%左右.

由于上述近似的最小时间间隔为1天，从而导致e≈0.0172和e≈0.0151两种结果，因此需要取平均值.更精确地选取春分、秋分的时间点，就可以避免这一问题.2021年秋分时间为9月23日03：20：55，春分为3月20日17：37：19，而2020年的秋分是9月22日21：30：32，取地球公转周期为365.2564日，将时间换算成小时，仍然按照（6）式进行计算，则有

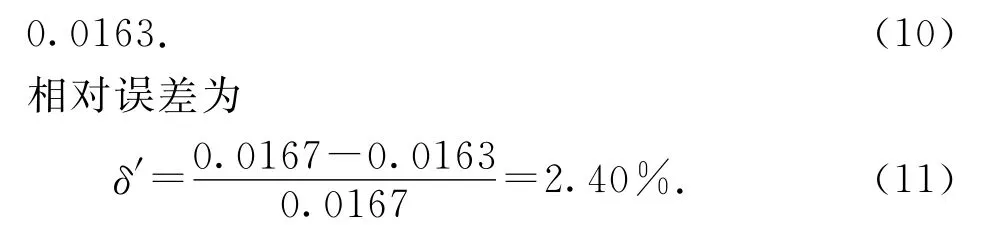
无论是（9）式还是（10）式，所得结果均略小于真实值，产生这一误差的原因在于计算中所做的近似方法.由图2可见，矩形A′B′C′D′的面积Sj大于ΔS，因此

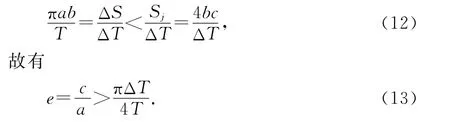
而（11）式则表明，该近似给出的结果虽然小于地球轨道偏心率的真实值，但是却非常接近.