变温热源热管式热电制冷器结构设计和性能分析

孟凡凯 陈赵军 徐辰欣

(海军工程大学动力工程学院，武汉 430033)

热电制冷技术无需制冷工质，通过半导体热电材料内部微观粒子运动和能量迁移实现连续固态制冷[1-3]，由于具有结构简单、紧凑、体积小、制冷迅速、环保等优点，已成为最有前途的制冷技术之一[4].近年来随着热电材料性能的不断提升，热电制冷已经广泛用于军事[5-6]、医疗[7]、家电[8-9]、电子设备散热[10-11]、电池热管理[12-14]、人体热防护[15-16]和膜蒸馏[17]等众多领域.

关于热电制冷的研究可分为2个主要方向[18]：一是关于半导体热电材料性能的研究，包括预测、发现和制造更高优值系数的热电半导体材料[19]；二是从热力学方面对基于现有热电材料热电制冷器的结构和散热方式进行改进和优化[20].热力学方面对热电制冷装置的研究可分为基于非平衡热力学的研究和将非平衡热力学与有限时间热力学相结合的研究[21].基于非平衡热力学理论[22]的研究，假定热电单元端面温度等于热源温度，不考虑外部换热器的影响，在热电制冷模块端面温度给定的情况下对装置进行分析.基于有限时间热力学理论[23]的研究充分考虑了冷、热源与热电制冷模块之间传热的不可逆性，分析设计参数和运行参数对装置的功率、效率以及热电制冷单元端面温度变化的影响，是对非平衡热力学的进一步扩展和补充，为热电制冷器工作特性的探索提供了新思路.许多学者将非平衡热力学与有限时间热力学相结合用于热电制冷装置的研究[24-27]，取得了许多有价值的成果.

热电制冷器常见的热端散热方式主要有空冷和水冷[28].有关空冷和水冷散热的热电制冷器的理论和实验研究，取得了许多有意义的研究成果[29-30].热管是一种利用液体工质相变进行热量传递的换热元器件，它可以通过很小的截面面积将大量的热量远距离传输而无需外加动力，具有良好的等温性、高效的导热性能和体积小等优势[31].近年来越来越多的研究表明，在微型化和高热流密度散热方面，相比空冷和水冷散热方式，将热管用于热电制冷器热端散热具有许多独特的优势[32-33].

目前关于热电制冷的研究大多是在恒温热源下进行的，关于变温热源热电制冷器的研究较少.本文在文献[34]的基础上，将热管用于热电制冷器热端散热，基于有限时间热力学理论，提出一种变温热源下热电冷却空气通道结构，考虑包括汤姆逊效应在内的各种热电效应，建立相应的热力学模型.通过建立一维热阻网络图，采用制冷率密度分析方法研究沿程温度变化和装置的制冷性能，以期获得输入电流、模块参数、管道厚度等关键参数对装置制冷性能的影响规律.

1 结构设计与热力学模型

本文设计的热管式热电制冷器装置主要由热电制冷模块和换热器2部分组成，装置模型如图1所示.图中，P和N分别表示P型热电单元和N型热电单元.装置热端采用热管散热器，冷端采用直肋热沉.装置为边长d1的正方形管道式结构，流体换热通道截面如图2所示.管道式通道长度为Lf，管内为被冷却的空气，管外为环境空气.

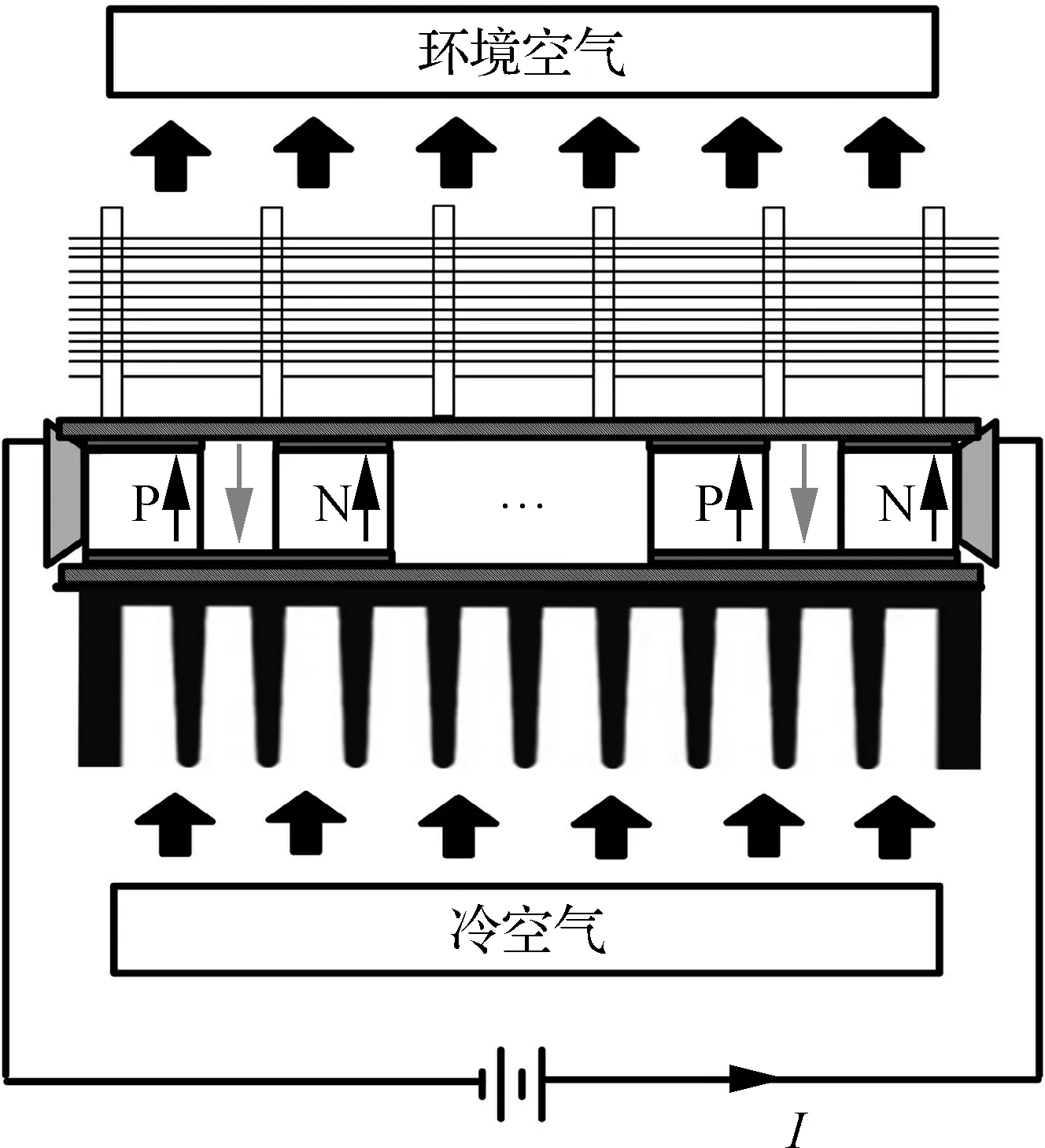
图1 热管式热电制冷装置模型

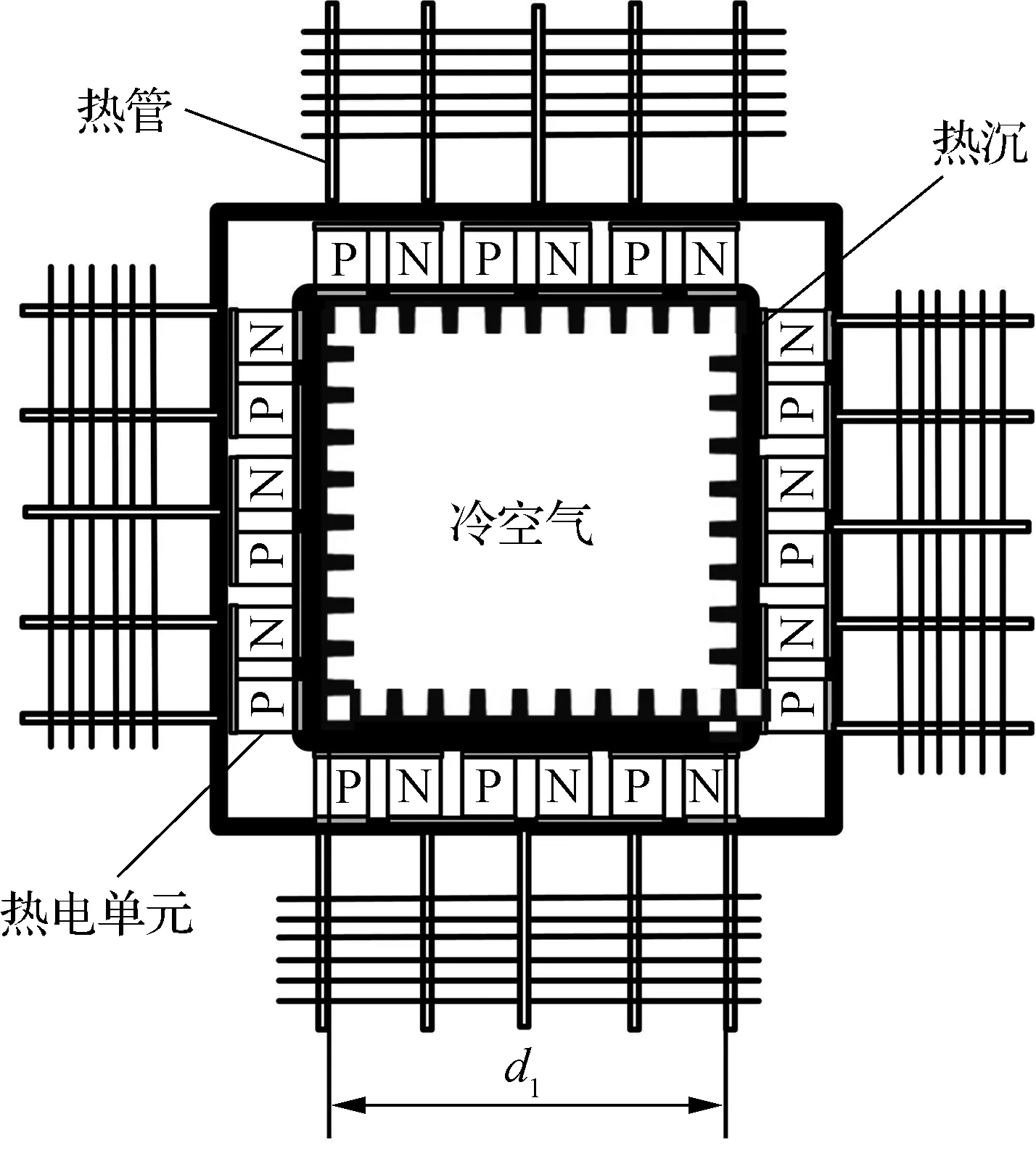
图2 流体换热通道截面

基于有限时间热力学理论，建立如图3所示的变温热源模型.装置低温热源为沿程放出热量的空气，温度随着管道长度Lf变化，为变温热源.高温热源为环境空气，温度不变，为恒温热源.环境空气和管道内空气温度分别为T1和T2(x)，其中x表示沿管道长度Lf方向的变化量.考虑高低温热源与热电模块端面间的有限速率传热，热电单元热端和冷端温度分别为Th(x)和Tc(x).出于电绝缘的要求，热电单元侧面不能相互接触，因此热电制冷模块内部存在空气间隙，这会导致一部分热量不经过热电偶臂而直接从空气间隙流过(如图1灰色箭头所示).这部分热流称之为空气间隙热漏，记作Qg.考虑制冷模块单元间的热漏损失，故引入填充系数ξ(0<ξ≤1)，定义为

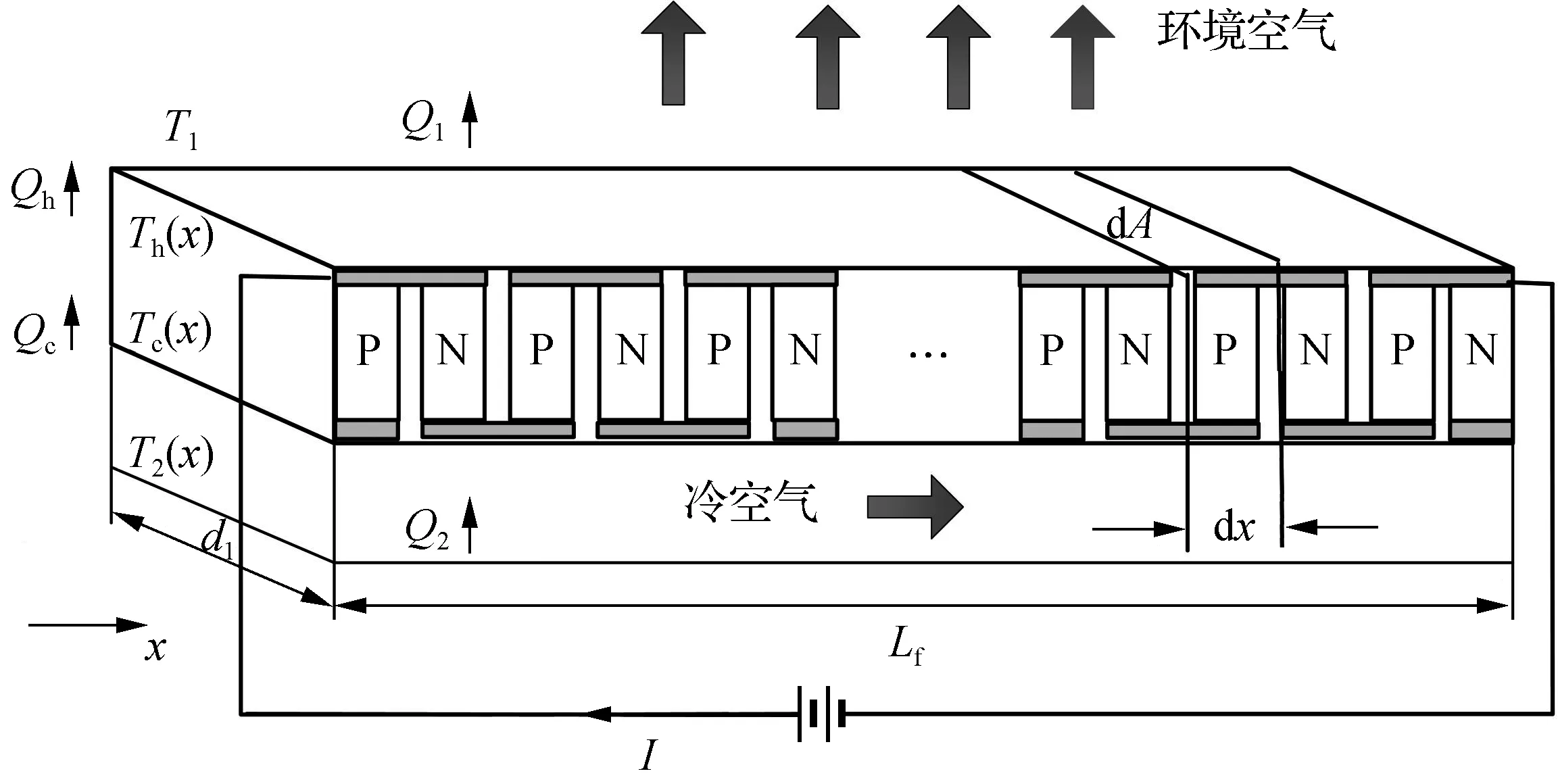
图3 装置变温热源模型

(1)

式中，A、N和Acp分别为热电单元横截面积、热电单元对数和制冷模块端面面积.

高、低温热源吸、放热流率分别为Q1和Q2，制冷模块放、吸热流率分别为Qh和Qc.换热管道长度和宽度分别为Lf和d1.高、低温热源空气质量流率分别为G1和G2，空气定压比热容为cp，工作电流为I.设低温热源空气进口温度为T2,in.

2 基本关系与模型求解

热管沿径向方向依次为管壳、管芯(或称吸液芯)和蒸汽腔.沿轴向方向，根据功能的不同，热管又可分为蒸发段(蒸发器)、绝热段和冷凝段(冷凝器)3部分.热管结构如图4所示，其中d0为热管外径，le、la、lc分别为蒸发段长度、绝热段长度、冷凝段长度，δg和δf分别为管壁和吸液芯厚度.本文采用普通常温铜水热管，即管壳材料为无氧铜，工质为水，吸液芯材料为200目的紫铜丝网.

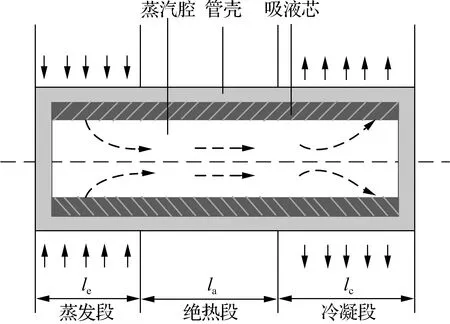
(a)热管轴截面

由于热电制冷模块热端(管外)与冷端(管内)均为空气与固体壁面的对流换热，热阻较大.为了增强换热，装置内部采用热沉换热器强迫风冷换热方式，外部采用热管换热器和风扇组合的换热方式.假设热电单元温度分布均匀，将装置的传热简化为一维传热.考虑到热阻大小与装置的结构尺寸有关，为了反映装置外部传热性能和将外部热阻统一基准，本文以热电制冷模块单位面积为基准，采用折算面积热阻法，装置的一维传热热阻网络如图5所示.图中,冷端和热端热阻分别用r1和r2表示，其均由4部分热阻组成，且各部分热阻均为折算面积热阻；rcp1、rc1、rex1和rcv1分别表示热端陶瓷基板导热热阻、接触热阻、换热器基板热阻和换热器对流热阻，rcp2、rc2、rex2和rcv2分别表示冷端陶瓷基板导热热阻、接触热阻、换热器基板热阻和换热器对流热阻；rP、rN和rg分别表示P型、N型热电单元的导热热阻和空气间隙热阻.

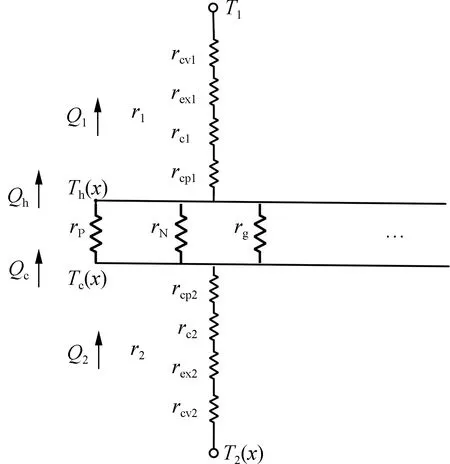
图5 装置热阻网络图

陶瓷基板导热热阻rcp为

(2)

式中，δcp和λcp分别为陶瓷基板厚度和陶瓷的热导率.

接触热阻rc为

(3)

式中，δc和λc分别为导热硅脂的厚度和热导率.

换热器基板热阻rex为

(4)

式中，δex和λex分别为换热器基板厚度和热导率.

热电制冷器热端的热量主要是通过热管蒸发段受热将液态工质蒸发变为蒸汽，然后蒸汽携带热量在压力差的作用下从蒸发段流向冷凝段，最后散发到环境中.忽略热管的辐射传热热阻与热管蒸发段的对流传热热阻，热管换热器对流传热热阻Rcv1主要由蒸发段到冷凝段之间的10个热阻组成[35]，即，蒸发段管壁径向导热热阻R1、蒸发段吸液芯径向传热热阻R2、蒸发段液-气相变热阻R3、蒸汽轴向流动热阻R4、冷凝段气-液相变热阻R5、冷凝段吸液芯径向导热热阻R6、冷凝段管壁径向导热热阻R7、管壁轴向传热热阻R8、吸液芯轴向传热热阻R9和冷凝段肋片与空气对流换热热阻R10.热管等效热阻一维网络图如图6所示.

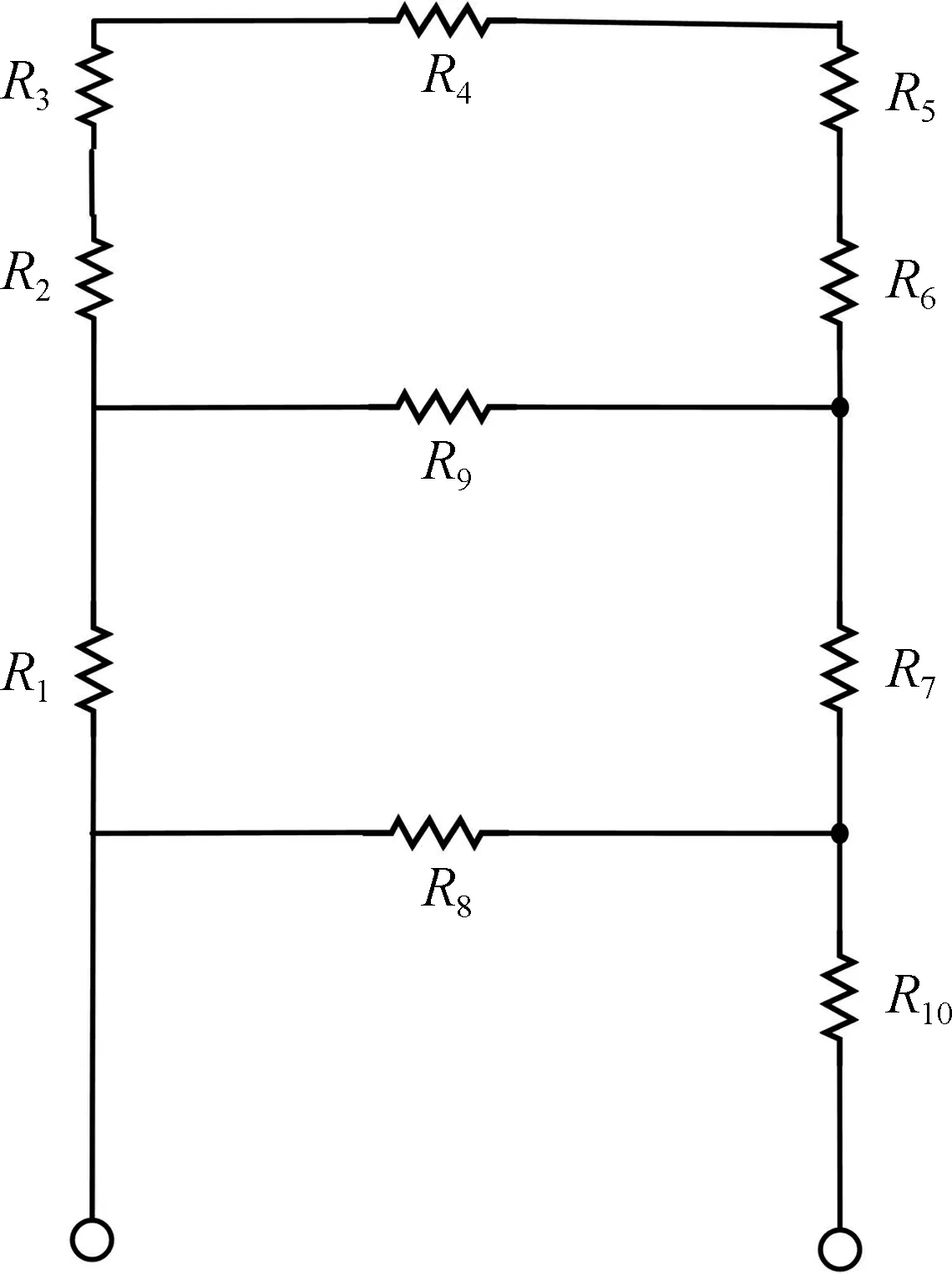
图6 热管等效热阻网络图

各部分热阻可由下式计算：

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

式中，l为热管总长度；λg和λf分别为管壁和吸液芯材料的导热系数；γ、Ro、Tv、Pv、Q和ΔPv分别为工质汽化潜热、气体常数、蒸汽温度、蒸汽饱和压力、传热量和热管内蒸汽相总压降.

热管换热器肋片与空气对流换热热阻计算式为

(14)

式(14)中，有效散热面积Aeff1采用下式计算：

(15)

式中，N1为肋片数；Lf1为肋长；H1为肋高；n为热管根数.

有效换热系数heff1采用下式计算[36]：

(16)

式中，A1、A2和A0分别为无肋部分面积、肋片表面积和裸管表面积.

式(16)中，肋效率ηf采用下式计算[36]：

(17)

(18)

式中，λ为肋片材料的导热系数；δ1为肋片厚度.

管外换热系数h1计算采用如下经验方程[36]：

(19)

式(19)适用条件为[36]

(20)

热管等效对流传热热阻为

(21)

折算为面积对流热阻为

(22)

冷端采用常见的等截面直肋热沉，面积对流换热热阻可表示为[37]

rcv2=

(23)

式中，δ2、ds2、H2、h2分别为热沉的肋厚、肋间距、肋高和热沉侧空气对流换热系数.

综上，热端和冷端热阻可分别表示为

r1=rcp1+rc1+rex1+rcv1

(24)

r2=rc2+rcp2+rex2+rcv2

(25)

沿管内空气流动方向取如图3所示的微元体积，考虑包括汤姆逊效应在内的各种内部效应，根据传热学以及非平衡热力学理论和有限时间热力学理论，有

(26)

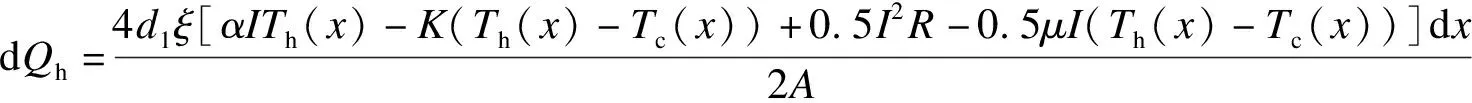
(27)

(28)

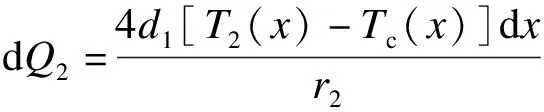
(29)

dQ2=-G2cpdT2(x)

(30)

式中，α、K、R和μ分别为塞贝克系数、总热导率、总电阻和汤姆逊系数.

空气间隙热漏为

(31)

式中，rg=L/kf，L为热电单元长度.

根据能量平衡方程，有

Q1=Qh-Qg

(32)

Q2=Qc-Qg

(33)

联立式(26)～(33)，得到Th(x)、Tc(x)和T2(x)的微分方程为

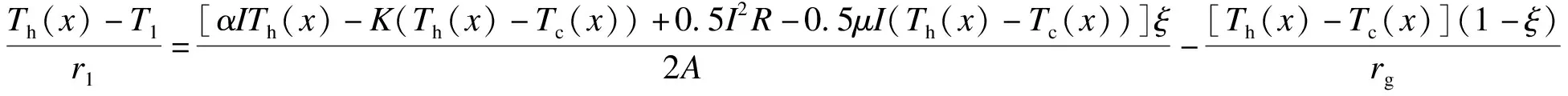
(34)

(35)

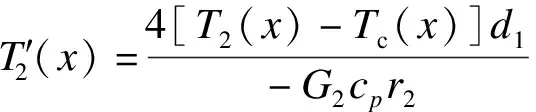
(36)

温度边界条件为

T2(0)=T2,in

(37)

高低温热源空气吸热和放热流率分别为

(38)

Q2=G2cp[T2(0)-T2(Lf)]

(39)

装置输入功率和制冷系数分别为

P=Q1-Q2

(40)

(41)

式(34)～(37)属于微分代数混合方程组初值问题，可利用MATLAB优化工具箱进行求解.参数给定后，可求得Th(x)、Tc(x)和T2(x)沿程温度变化，然后代入式(38)～(41)，即可得到装置的制冷率密度、输入功率和制冷系数随各参数的变化关系.

3 影响参数分析

数值计算中，采用传统热电材料碲化铋(Bi2Te3)，热电模块型号为TEC12706，尺寸大小为40 mm×40 mm×4 mm，由127个热电单元组成.热电单元截面积A=1.44 mm×1.44 mm，长度L=2 mm，计算可得填充系数ξ=0.329.T取热电偶热端与冷端的平均温度，考虑材料的变物性，采用热电单元P型和N型臂的参数拟合公式为[38]

αP=-αN=10-9(22 224.0+930.6T-0.990 5T2)V/K

(42)

ρP=ρN=10-10(5 112.0+163.4T+0.627 9T2)Ω·m

(43)

KP=KN=10-4(62 605.0-277.7T+0.413 1T2)W/(m·K)

(44)

μP=-μN=10-9(930.6T-1.981T2)V/K

(45)

式中，αP和αN分别表示P型和N型臂的塞贝克系数；ρP和ρN分别表示P型和N型臂的电导率；KP和KN分别表示P型和N型臂的热导率；μP和μN分别为P型和N型臂的汤姆逊系数.

目前关于热电制冷器的研究，大多以装置的总制冷率为性能指标.由于装置的制冷率与热电制冷模块总数有关，总制冷率的大小并不能反映装置的设计水平和制冷性能的优劣.因此，为了适用于不同规格型号的热电制冷器，并反映热电模块单位面积下的制冷能力，本文采用制冷率密度分析方法，即以单位面积模块的制冷率为性能指标.定义制冷率密度q2为

(46)

式中，Nmod和Amod分别为总模块数和单个模块面积.

空气的比热容为cp=1.005 J/(g·K)，管内冷源空气流速取为u2=5 m/s.取管道宽度d1=0.2 m，流道长度Lf=2 m.

3.1 热阻分析和沿程温度变化规律

图7给出了热端和冷端每部分热阻的分布图，从左往右依次为陶瓷基板热阻rcp、接触热阻rc、换热器基板热阻rex和换热器对流换热热阻rcv.可见热端和冷端最大热阻均为对流换热热阻，因此换热器的设计是影响热电制冷器性能的重要因素，也是结构设计的关键环节.此外，通过对比热端和冷端对流换热热阻可知，热管对流换热热阻明显小于热沉对流换热热阻，表明热管散热方式可有效减小外部传热热阻，提升装置性能.

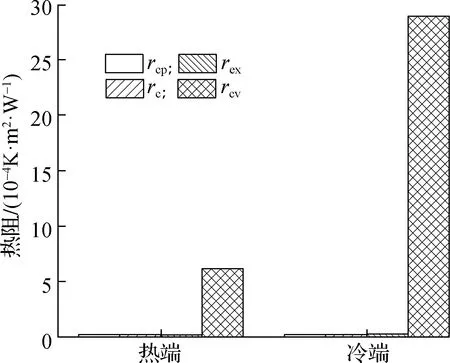
图7 热端和冷端热阻分布

图8给出了电流I=2.5 A时，模块热端温度Th、管内低温热源温度T2和模块冷端温度Tc与管道长度Lf的关系.由图可知，因为环境温度保持不变，且热管散热性能较好，热端热流密度变化很小，从而热端温度Th几乎保持不变.由于冷源空气在流动过程中释放热量，故管内低温热源温度T2和模块冷端温度Tc随着管道长度Lf的增加均减小.计算结果表明，对于管道宽度d1=0.2 m，管内冷空气流速u2=5 m/s，管道长度Lf=2 m，入口温度为290 K时，每米流程低温热源温度T2降低约 14 K.

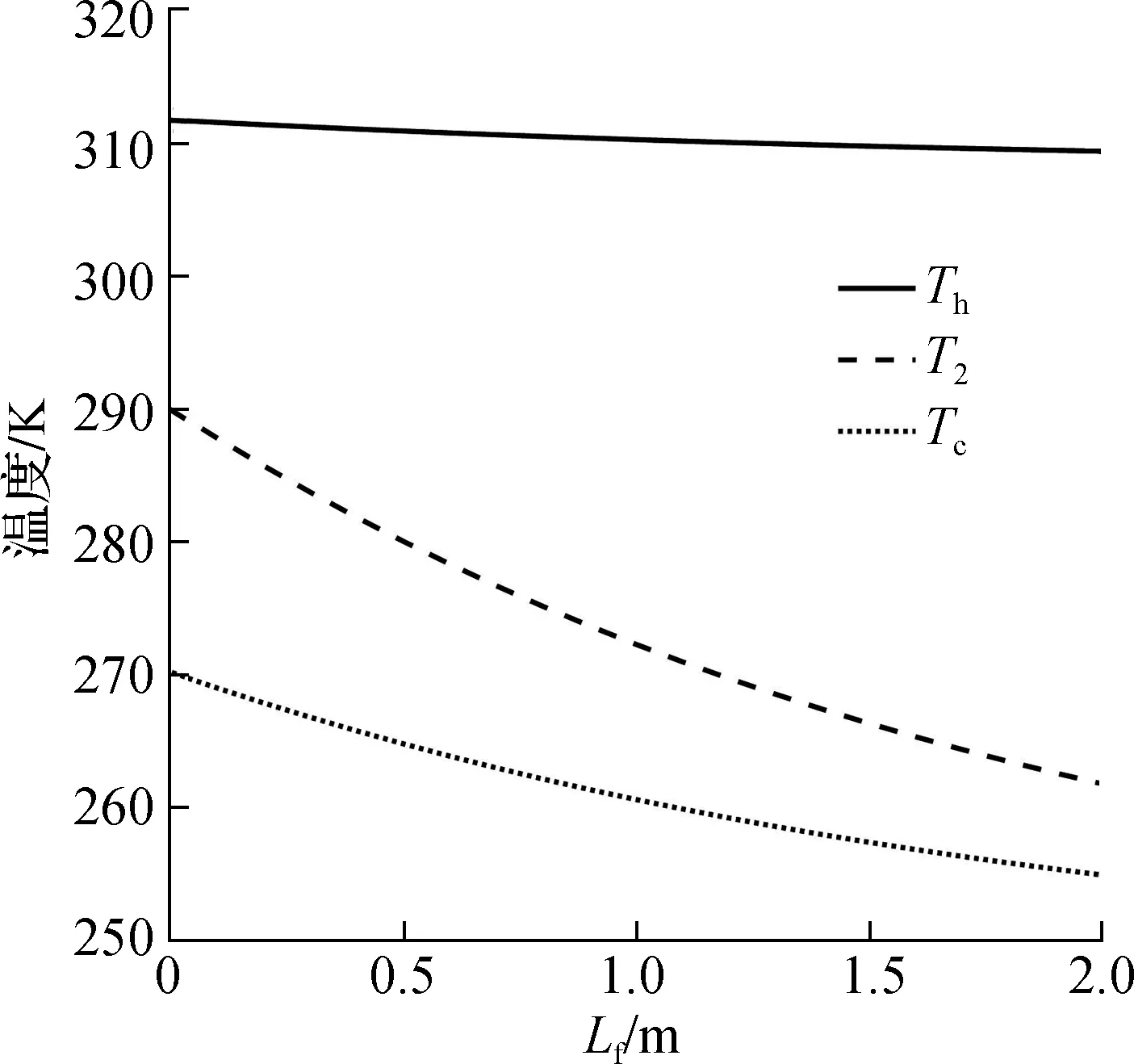
图8 沿程温度变化与管道长度的关系

3.2 输入电流的影响

图9给出了不同冷空气入口温度下电流对装置制冷性能的影响，图9(a)和(b)分别表示制冷率密度q2和制冷系数ε与工作电流I的关系.由图可知，装置在同一工作电流下工作时，随着入口温度的降低，制冷率密度和制冷系数均减小.此外，在同一入口温度下，制冷率密度和制冷系数都对电流存在极值，即都随着电流的增大先增大后减小，但是二者的变化曲线完全不同.最大制冷率密度对应的最佳工作电流Iq2大于最大制冷系数对应的最佳工作电流Iε，这表明制冷率密度和制冷系数无法同时取得最大值，且对应的最佳工作电流相差较大，装置制冷能力和经济性能难以兼顾.当入口温度T2,in=290 K时，最大制冷系数εmax=1.11，对应的最佳工作电流Iε=0.55 A；最大制冷率密度q2max=0.48 W/cm2，对应的最佳工作电流Iq2=3.95 A，综合考虑经济性能和制冷性能，最佳工作电流的选取应介于0.55～3.95 A之间.在以下恒定电流运行分析时，均取工作电流I=2.5 A.

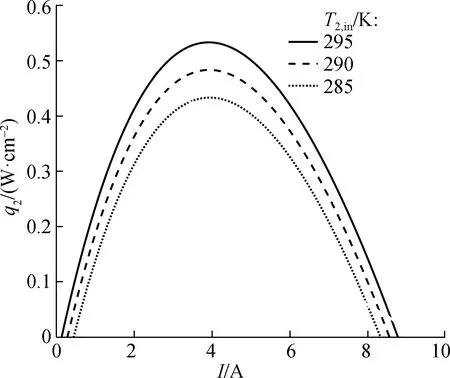
(a)制冷率密度与电流的关系

图10给出了考虑空气间隙热漏和不考虑间隙热漏2种情况下，制冷率密度和制冷系数随工作电流的变化关系.由图可知，当入口温度T2,in=290 K时，相比于不考虑模块间的空气间隙热漏的情形，考虑模块间的空气间隙热漏能够降低制冷率密度和制冷系数，但降低的幅度很小.不考虑空气间隙热漏时最大制冷率密度和最大制冷系数分别为 0.50 W/cm2和1.17,考虑空气间隙热漏时最大制冷率密度和最大制冷系数分别为0.48 W/cm2和1.11，分别降低了约4.00%和5.13%.

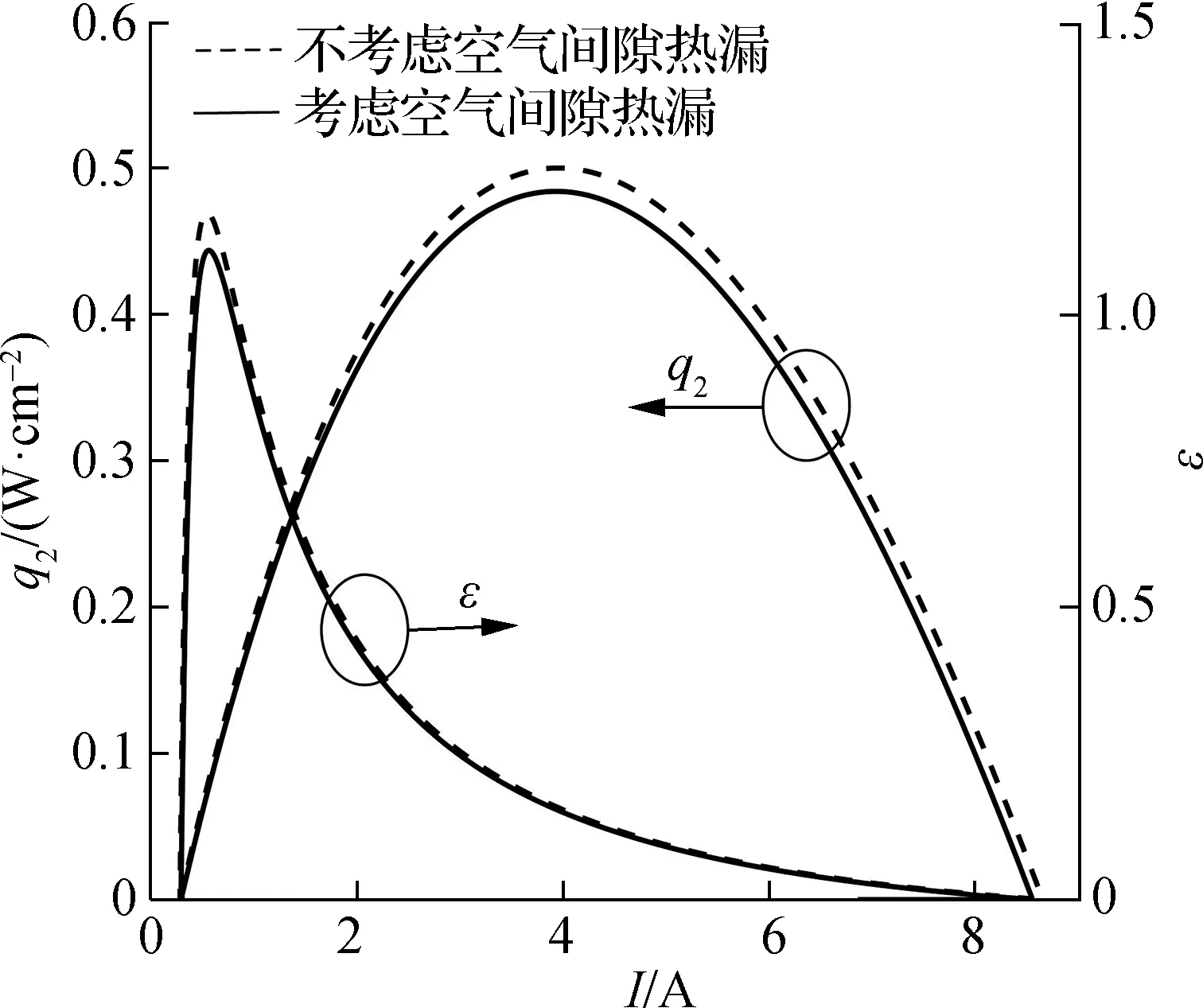
图10 空气间隙热漏对装置性能的影响

3.3 模块结构参数的影响

热电模块的结构设计参数是影响热电制冷器性能的重要因素之一.图11给出了模块结构参数对装置制冷性能的影响，图11(a)和(b)分别给出了不同入口温度下制冷率密度q2和制冷系数ε与制冷模块填充系数ξ的关系.由图可知，在一定的入口温度下，随着填充系数的增大，制冷率密度和制冷系数均先增大后减小，存在极值.当入口温度T2,in分别为285、290和295 K时，最大制冷率密度q2max分别为0.38、0.43和0.49 W/cm2，与之对应的最佳填充系数ξq2分别为0.44、0.45和0.47.由式(24)可知，热流密度与填充系数成正比关系，随着填充系数的增大，热流密度增大，因此制冷率密度增大.热流密度增大的同时热端热阻保持不变，从而导致热端温度升高，当热端与冷端之间的空气间隙热漏增大速度大于制冷率密度增加的速度时，冷端温度会开始升高，因此制冷率密度开始下降.最大制冷系数εmax分别为0.82、0.99和1.20，与之对应的最佳填充系数ξε分别为0.03、0.02和0.01.填充系数增大会使模块热阻减小，从而端面温差减小，导致制冷系数减小.热电制冷器热电偶数目增多或者热电单元截面积增大均会增大填充系数.因此，在实际设计中要协调制冷性能和经济性能，合理选取填充系数.要想获得较好的制冷性能，应该选取较大的填充系数；反之，要想获得较大的制冷系数，应该选取较小的填充系数.

图11(c)和(d)分别给出了不同入口温度下制冷率密度q2和制冷系数ε与热电单元长度L的关系.由图可知，一定入口温度下，分别存在最佳的热电单元长度使得制冷率密度和制冷系数取得最大值.当入口温度分别为285、290和295 K时，最大制冷率密度q2max分别为0.42、0.46和0.49 W/cm2，对应的最佳热电单元长度Lq2分别为3.11、3.05和3.01mm；最大制冷系数εmax分别为0.31、0.37和0.46，与之对应的最佳热电单元长度Lε分别为1.31、1.01和0.71 mm.这表明随着入口温度的增加，最大制冷率密度和最大制冷系数均增大，与最大制冷率密度对应的最佳热电单元长度几乎不变，与最大制冷系数对应的最佳热电单元长度减小.

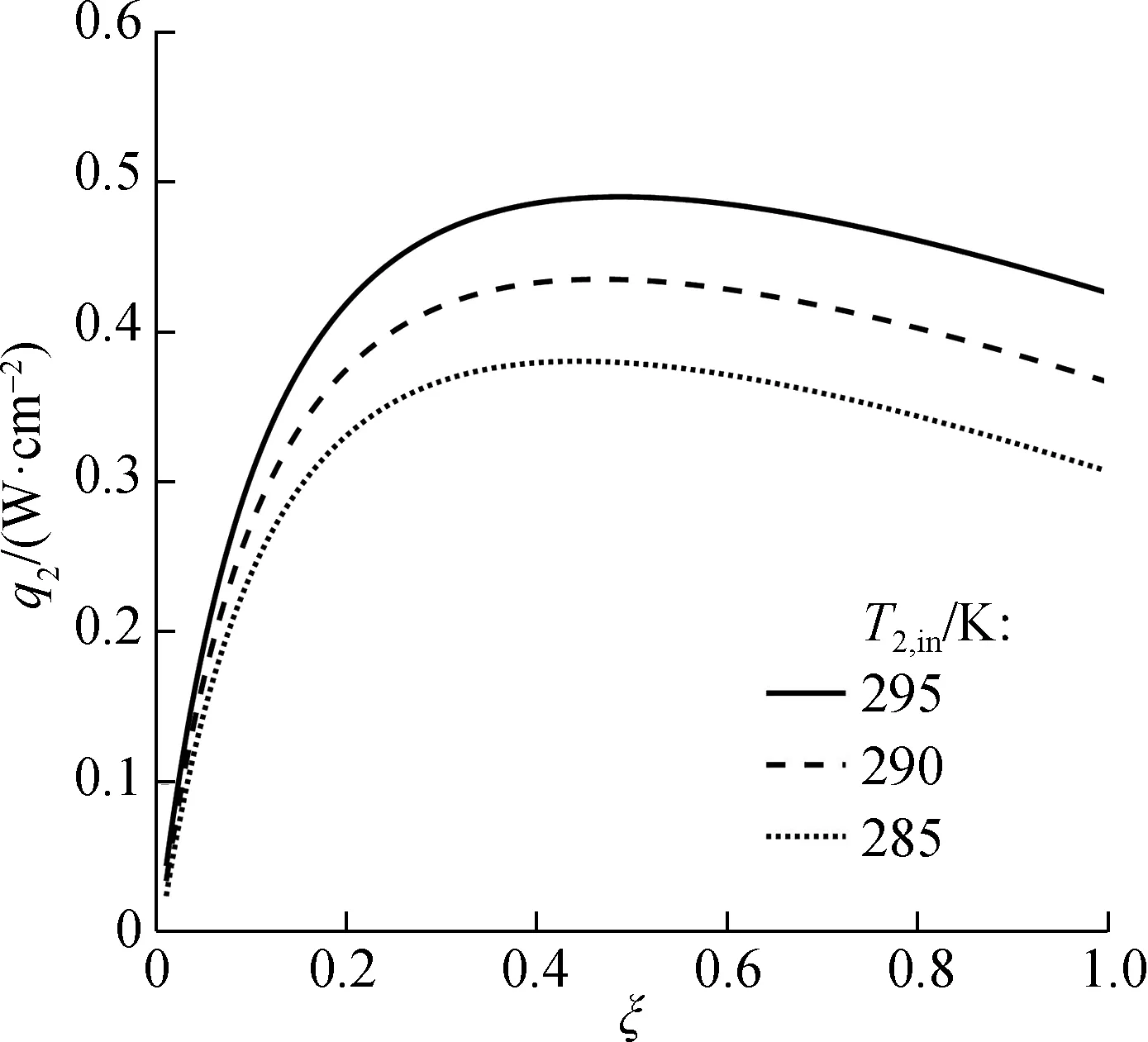
(a)制冷率密度与填充系数的关系

3.4 管道宽度的影响

冷空气沿程温度变化与管道宽度和冷空气流速有较大关系，在实际应用中需合理选取管道尺寸.图12给出了不同冷空气流速下管道宽度对装置性能的影响，图12(a)和(b)分别给出了不同空气流速下制冷率密度q2和制冷系数ε与管道宽度d1的关系.由图可知，当流速一定时，制冷率密度和制冷系数随着管道宽度的增大而增大.由式(39)可知，制冷率密度正比于质量流率，并且质量流率越大，温度变化越小，故当其他条件不变时，增大管道宽度能够增大质量流率，有利于提升制冷性能.当管道结构尺寸固定时，增大冷空气流速也能够增大制冷率密度和制冷系数，这是因为一方面增大流速能够增大流量，另一方面增大冷空气流速能够增大换热系数，减小冷端热阻，有利于增强换热.当空气流速小于5 m/s时，提高流速，制冷率密度和制冷系数明显增大，装置性能提升显著；但是当冷空气流速大于5 m/s时，流速的提高对制冷率密度和制冷系数的影响较小.

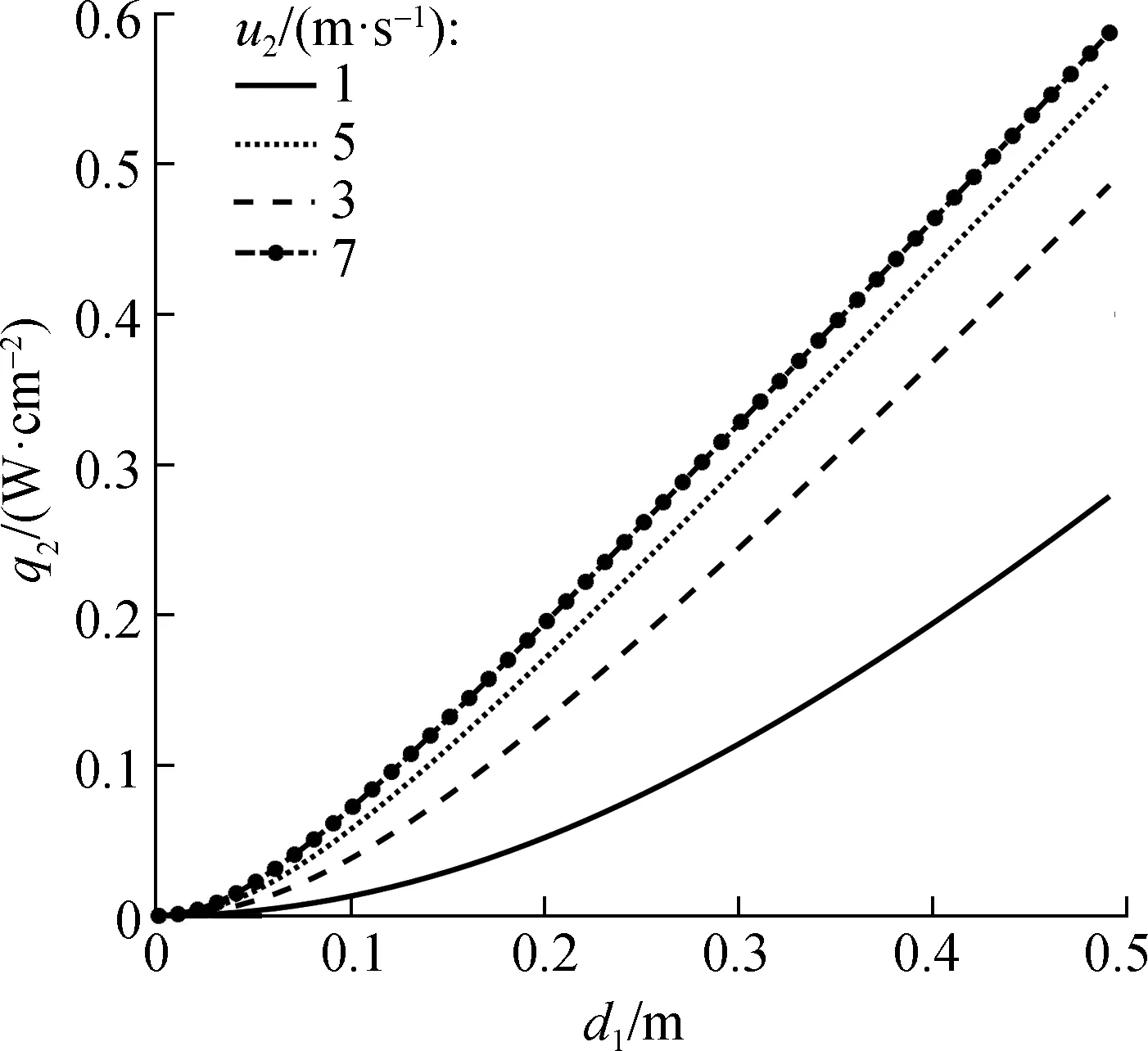
(a)制冷率密度与管道宽度的关系

3.5 吸液芯厚度的影响

吸液芯毛细结构是热管的核心组成部分，其厚度能够直接影响热管的散热性能.图13给出了吸液芯厚度对装置性能的影响，图13(a)和(b)分别给出了不同入口温度下装置制冷率密度q2和制冷系数ε与吸液芯厚度δf的关系.由图可知，装置在一定的入口温度下工作时，增大吸液芯厚度会降低制冷率密度和制冷系数.当吸液芯厚度小于2 mm时，吸液芯厚度对制冷率密度和制冷系数影响较小，当厚度大于2 mm时，制冷率密度和制冷系数迅速降低，制冷性能恶化.这是因为当热管其他几何条件一定时，增大吸液芯厚度导致蒸汽流通空间变小，蒸汽流通受阻，换热变弱，热管散热变差，热端热量不能及时排出，导致制冷性能恶化.

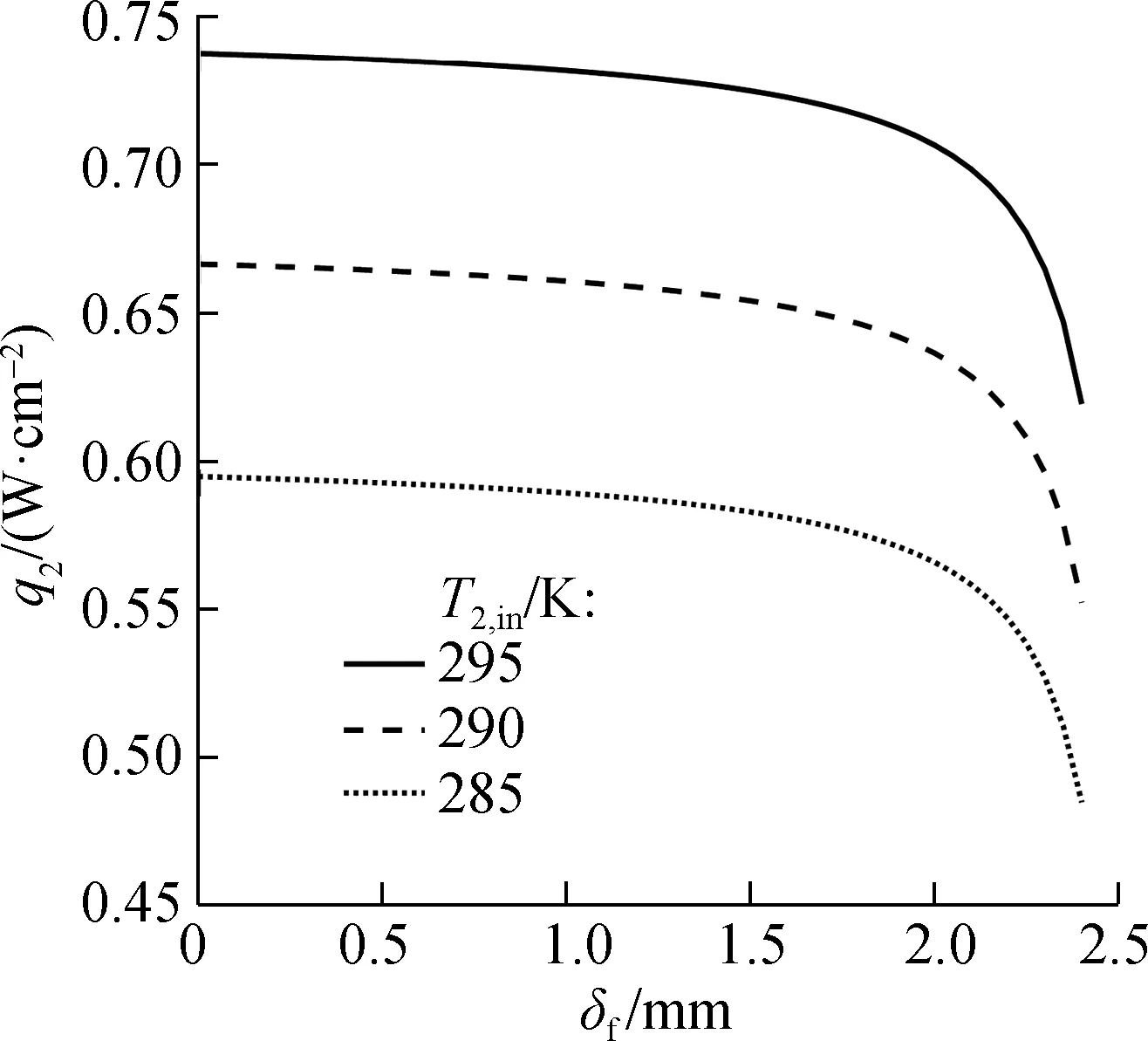
(a)制冷率密度与吸液芯厚度的关系

4 结论

1)当管道宽度d1=0.2 m，管道长度Lf=2 m，管内冷空气流速u2=5 m/s，入口温度T2,in=290 K时，每米流程冷空气温度T2降低约14 K.相比于不考虑模块间的空气间隙热漏的情形，相同工况下考虑模块间的空气间隙热漏使得制冷率密度和制冷系数均降低，最大制冷率密度和最大制冷系数分别为0.48 W/cm2和 1.11，最大制冷率密度和最大制冷系数分别降低了约4.00%和5.13%.

2)综合考虑经济性能和制冷性能，当入口温度为290 K时，最佳工作电流区间介于0.55～3.95 A之间.

3)同一入口温度下，存在最佳的热电单元长度使得制冷率密度和制冷系数分别取得最大值.随着入口温度的增加，最大制冷率密度和最大制冷系数均增大.对应最大制冷率密度的最佳热电单元长度基本不变，最大制冷系数的最佳热电单元长度减小.

4)当空气流速小于5 m/s时，提高流速，制冷率密度和制冷系数明显增大，装置性能提升显著.但是当空气流速大于5 m/s时，流速的提高对制冷率密度和制冷系数的影响较小.

5)当吸液芯厚度小于2 mm时，吸液芯厚度对制冷率密度和制冷系数影响较小；当厚度大于2 mm时，制冷率密度和制冷系数迅速降低，制冷性能恶化.在实际设计中吸液芯厚度应小于2 mm.