土岩复合地层中深基坑开挖对邻近管线变形影响分析
2022-04-18丁建文廖赵胜
焦 宁 丁建文 吉 锋 郭 康 廖赵胜
(1东南大学交通学院,南京 211189)(2南水北调东线江苏水源有限责任公司,南京 210029)(3杭州谐云科技有限公司,杭州 310023)
我国第1条地铁线路建立于20世纪60年代,截止2021年7月,全国共计48座城市开通了轨道交通,线路共计246条,总运营里程达到了7 961 km,实际开行列车269×104列次[1].经过多年的发展,轨道交通已成为城市公共交通中重要的组成部分.随着城市化进程的不断加快,轨道交通由于具有准时、速达、大运量等优势,逐渐成为解决人们出行的主要公共交通工具.
轨道交通工程建设面临的主要技术难题为深基坑问题.深基坑开挖使得基坑周围土体原有应力平衡状态被打破,土体中应力重新分布,导致地面沉降和邻近管线不均匀沉降.然而,地下管线抵抗变形的能力具有一定限度,如果管线变形量过大,易导致管线无法正常使用,甚至引起重大安全事故[2-3].
地铁深基坑工程周围的市政管线管道较多,管线变形分析控制一直以来都是地铁深基坑的难点,主要研究方法包括理论分析[4-8]、现场实测[9-11]和数值模拟[12-17].
在理论分析方面,求解管线变形常采用弹性地基梁模型,其中Winkler地基模型应用最为广泛,但其忽略了地基变形的连续性,因而许多研究在此基础上提出了改良的双参数模型.文献[4]在Winkler地基模型的基础上引入剪切模量,提出了Pasternak 模型,可以较好地反映出土体在垂直方向上的实际剪切效应.文献[5]提出了一种考虑地基非线性变形、邻近弹簧和隧道向上位移相互作用的非线性Pasternak地基模型(NPFM),用于模拟与卸载应力相关的隧道-土相互作用.文献[6]给出了一种基于改进Winkler模量的Winkler解,用于分析隧道开挖对管线变形的响应.文献[7]提出了抛物型滑坡动力作用下的管道-土分离模型,并基于Winkler地基模型推导出该模型的封闭解析解.文献[8]运用修正Vlasov模型中的迭代流程,计算出Pasternak模型的关键参数弹性系数与剪切系数.
在现场实测方面,通过信息化施工监测手段,可以及时了解施工过程中管线沉降等各种参数的动态变化,对优化设计方案、发现不良变化后及时采取合理保护措施以预防事故发生具有重要意义.随着电子信息技术的发展,许多学者对新型、综合性基坑监测系统进行了研究.隋海波等[9]设计了一套基于BOTDR的新型基坑工程分布式光纤传感监测系统,可对管线的变形和泄漏进行监测, 了解地下管线位移和变形动态.齐红升等[10]开发了一套深基坑智能联网监测与预警系统,实现了信息集中管理、监测数据实时读取、自动存储查询、图表自动绘制、自动预警报警等一系列功能.Wu等[11]提出了一种基于无人机图像的基坑施工安全快速监测与分析方法,通过局部变形分布来评价基坑的局部安全状态.
在数值模拟方面,杜金龙等[12]运用FLAC3D有限元软件分析了不同管径大小对管线位移及变形的影响.赵平等[13]利用 MIDAS-GTS 三维有限元软件进行数值模拟,重点分析了临近管线材质、管线位置的改变在基坑开挖过程中对管线位移的影响.Zhang等[14]建立了管道与基坑的三维模型,通过数值模拟分析研究了管道参数、基坑参数、土体参数和地下连续墙对管道应力、应变和变形的影响.冯晓腊等[15]采用有限元软件PLAXIS进行基坑开挖数值模拟,分析了复杂条件下基坑支护结构体系及周边环境的受力、变形情况.金祎等[16]运用PLAXIS有限元软件模拟了基坑开挖引起大直径管线位移的变化,分析了基坑开挖引起管线水平和竖向位移之间的差异变化.施有志等[17]采用考虑土体小应变刚度特性的有限元方法,针对基坑施工对邻近管线的影响规律进行了参数分析,并划分了基坑开挖对邻近管线的影响分区.
目前,学者们主要针对单一土质或岩质地层的深基坑工程进行研究.然而,我国许多地区存在上土下岩的复合地层,针对这类地层中深基坑开挖对管线变形的影响研究较为缺乏.本文以南京地铁一号线北延工程二桥公园站车站深基坑为依托工程,基于现场监测数据进行管线变形分析,并结合实际工况,运用PLAXIS 3D有限元软件进行数值模拟,探究在土岩复合地层中深基坑开挖对邻近管线变形的影响,揭示基坑开挖深度、管线埋深等因素对管线变形的影响规律,并分析各因素的影响程度.
1 工程概况
南京地铁一号线北延工程二桥公园站位于栖霞区太新路,沿太新路方向设置.车站起止里程为YK23+107.865~YK23+431.850,地下2层岛式站台,局部3层,站台宽度为11.2 m,标准段宽度为22.5 m,总长度为325.5 m.其中,一期基坑长175.6 m,车站地形起伏较大,标准段底板埋深18.5~23.84 m.平行于太新路沿路中敷设有1根钢筋混凝土材质的DN1200污水管线,埋深约3 m,距车站基坑水平距离约11.3 m;平行于太新路方向沿路边埋设有1根PE材质的DN600给水管,在施工前迁改至基坑北侧约6.5 m处.
根据工程地质条件、基坑开挖深度及周边环境,二桥公园站车站基坑采用顺作法总体施工方案,最大开挖深度为23.1 m.如图1所示,基坑支护采用排桩+内支撑支护方式,围护桩采用φ1 000 mm@1 400 mm钻孔灌注桩,C25混凝土,端头井竖向设置4道支撑,标准段竖向设置3道支撑,首道为钢筋混凝土支撑,其余为钢支撑.明挖车站基坑所处地层为上软下硬复合地层,上部为杂填土和黏土层,下部为强风化和中风化砂岩,车站基底大多位于中风化、微风化砂岩层,局部位于可塑~硬塑粉质黏土层.场地未见地表水,地下水主要为松散岩类孔隙潜水、基岩裂隙水,水量较少.
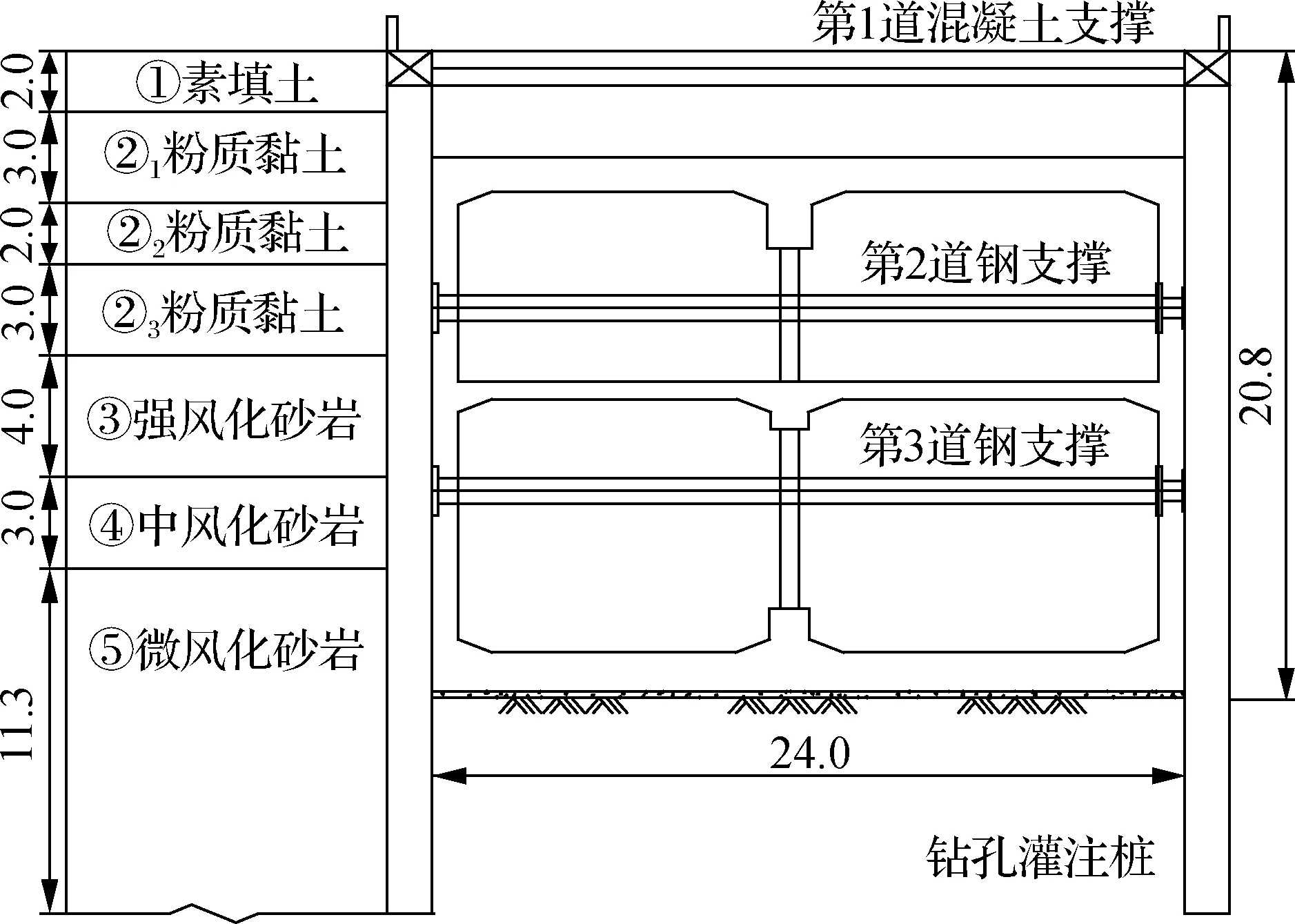
图1 基坑典型剖面图(单位:m)
2 现场实测数据分析
在基坑开挖过程中,针对基坑北侧的DN600给水管、DN1200污水管2条管线布设并监测了管线沉降监测点位,因不具备开挖条件且无检查井,采用间接布点方式在对应地表位置埋设间接观测点.如图2所示,点位间距约为10 m,依次命名为A01~A22、B01~B22.自2018-01-02基坑开挖开始监测,2018-07-20主体结构施工完毕停止监测,共计监测200 d.为便于分析,以基坑长度方向的中轴线为x轴,以基坑西侧边及延长线为y轴,建立直角坐标轴,以管线沉降监测点位的横坐标x表示其距离基坑西侧短边的水平距离.选取所有监测点位的最终沉降数据和特征点位整个基坑开挖过程的监测数据,绘制特征点位竖向位移时程曲线和管线最终竖向位移对比图.
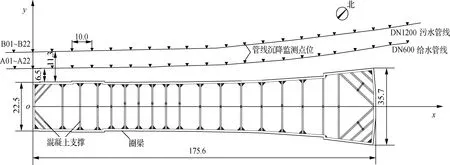
图2 管线沉降监测点位布设示意图(单位:m)
图3为2条管线的特征点位竖向位移时程曲线.由图可见,监测点位的竖向位移整体上呈下降趋势,并且随着基坑的开挖,沉降量逐渐增大.随着监测点位横坐标的增大(即监测点位越靠近基坑中部),沉降量逐渐增大,但增量逐渐减小.对比2条管线相同横坐标的监测点位在相同时间的沉降数据发现,DN600给水管的沉降量均大于DN1200污水管.观察数据整体变化情况可知,与后者相比,前者不同点位之间数据变化的一致性和稳定性较弱,波动性较强.究其原因在于,前者管径较小,与基坑的间距较小,埋深较浅,且埋设时间相对较短.
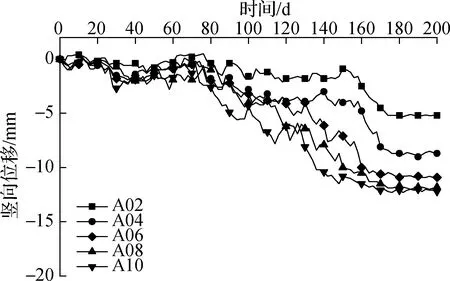
(a)DN600给水管
基坑开挖完成后管线的最终沉降见图4.由图可见,对于相同横坐标的监测点位,DN600给水管的最终沉降量均大于DN1200污水管,且越靠近基坑中部差值越大,最大差值为5.6 mm.随着基坑的开挖,管线会发生不均匀沉降.基坑开挖完成后,管线最终呈现出中间沉降大、两头沉降小的凹槽形,横坐标40~140 m范围内监测点位的沉降量相差较小,0~40 m和140~180 m范围内监测点位的最终沉降量则相差较大,这与文献[12]的结论相符.由此可知,基坑端部20%开挖长度范围内发生的不均匀沉降最大.在基坑开挖过程中,应在施工前对处于基坑端部范围内的管线加以特别保护,常用方法包括改迁法、悬吊法、绑吊法、隔离法等.
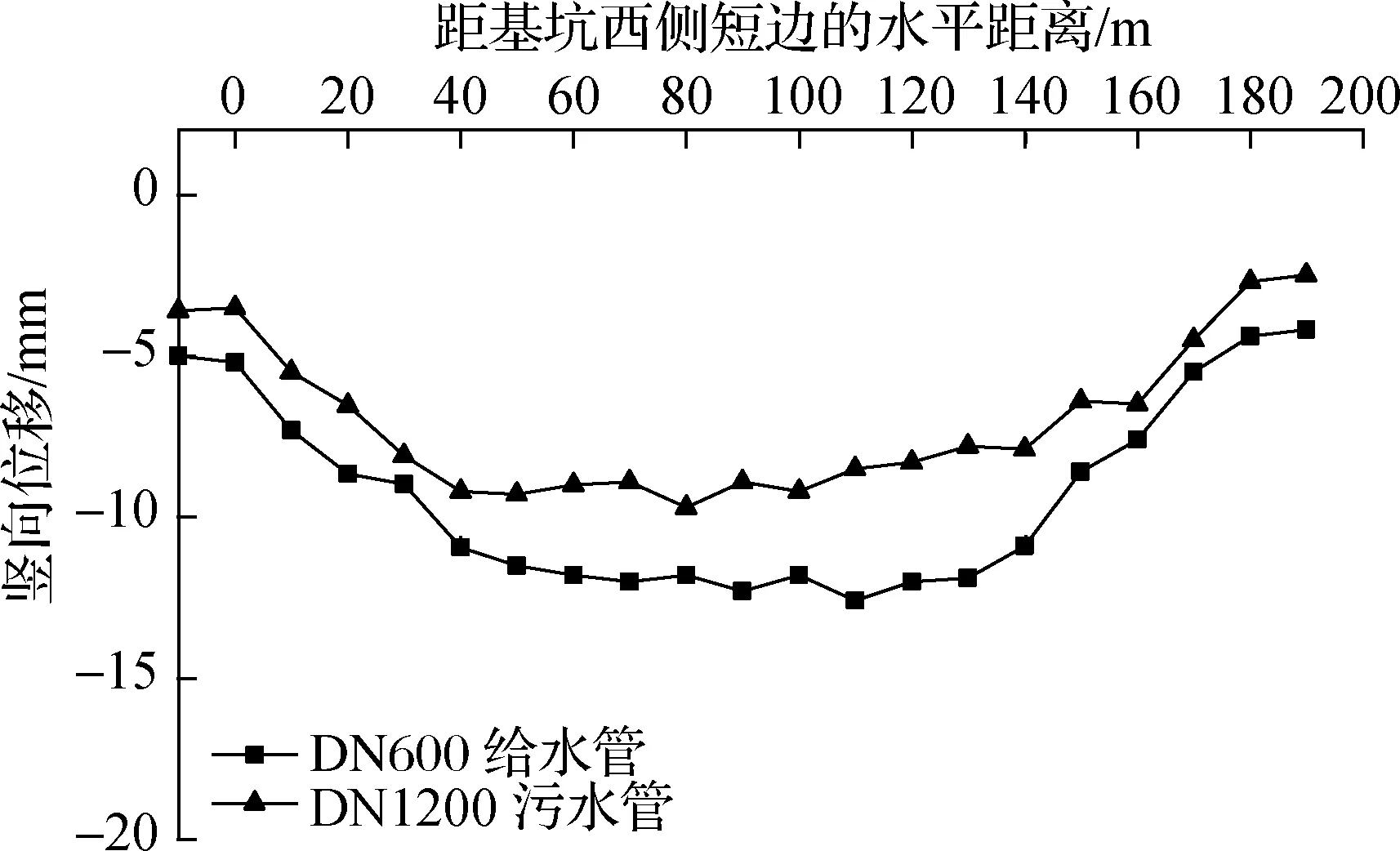
图4 基坑开挖完成后管线的最终沉降
选取基坑开挖对邻近管线影响的典型案例[18-19],与本工程的管线监测数据进行对比分析.除基坑所处地层不同之外,3个案例的管线材质、管线埋深、管线与基坑间距等其他因素基本相同或相似.文献[18]中基坑开挖深度均值为16 m,基坑开挖深度范围内为以杂填土、素填土和粉质黏土为主的单一地层,管线的最大沉降量为基坑开挖深度均值的 0.083%.文献[19]中基坑开挖深度均值为30.2 m,开挖深度范围内为由填土、泥质黏土和粉质黏土组成的软黏土地层,管线的最大沉降量为基坑开挖深度均值的0.298%.本文中土岩复合地层中管线的最大沉降量为基坑开挖深度均值的0.042%,明显小于另外2个单一地层中管线的最大沉降量,仅为文献[18]的50.6%,文献[19]的14.1%.由此可知,与单一土层相比,在上土下岩的土岩复合地层中进行基坑开挖时邻近管线的沉降变形相对较小.
3 数值模拟分析
3.1 三维数值分析模型
为进一步分析各因素对邻近管线变形的影响规律,运用PLAXIS 3D软件进行数值模拟分析.基于车站一期基坑的典型断面,有限元模型中取基坑的开挖深度为20 m,宽为24 m.由于基坑两边对称,为简化计算,取1/2基坑长度进行建模,模型尺寸为160 m×100 m×40 m,模型的边界条件为四周侧面限制水平位移,底部设置固定约束.
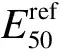

表1 土体模型参数

表2 岩体模型参数
因数值建模与实际工程相比不可避免具有一定的差异性,因此假设地下管线满足以下条件:地下管线连续、无原生缺陷和破损;不考虑管线内压力及管线内流体对管线的作用,假设管线密度与该土层密度相近;将地下管线视为线单元,不考虑管线横截面尺寸.
采用PLAXIS 3D软件提供的梁单元模拟地下管线,参照DN1200污水管的实际参数,管线与基坑间距取12 m,埋深取3 m,管径取1.2 m,惯性矩为0.109 m4,弹性模量为28 GPa2,密度为2.6 kg/m3.根据基坑模型参数和管线参数建立基坑和管线的三维模型,结果见图5.
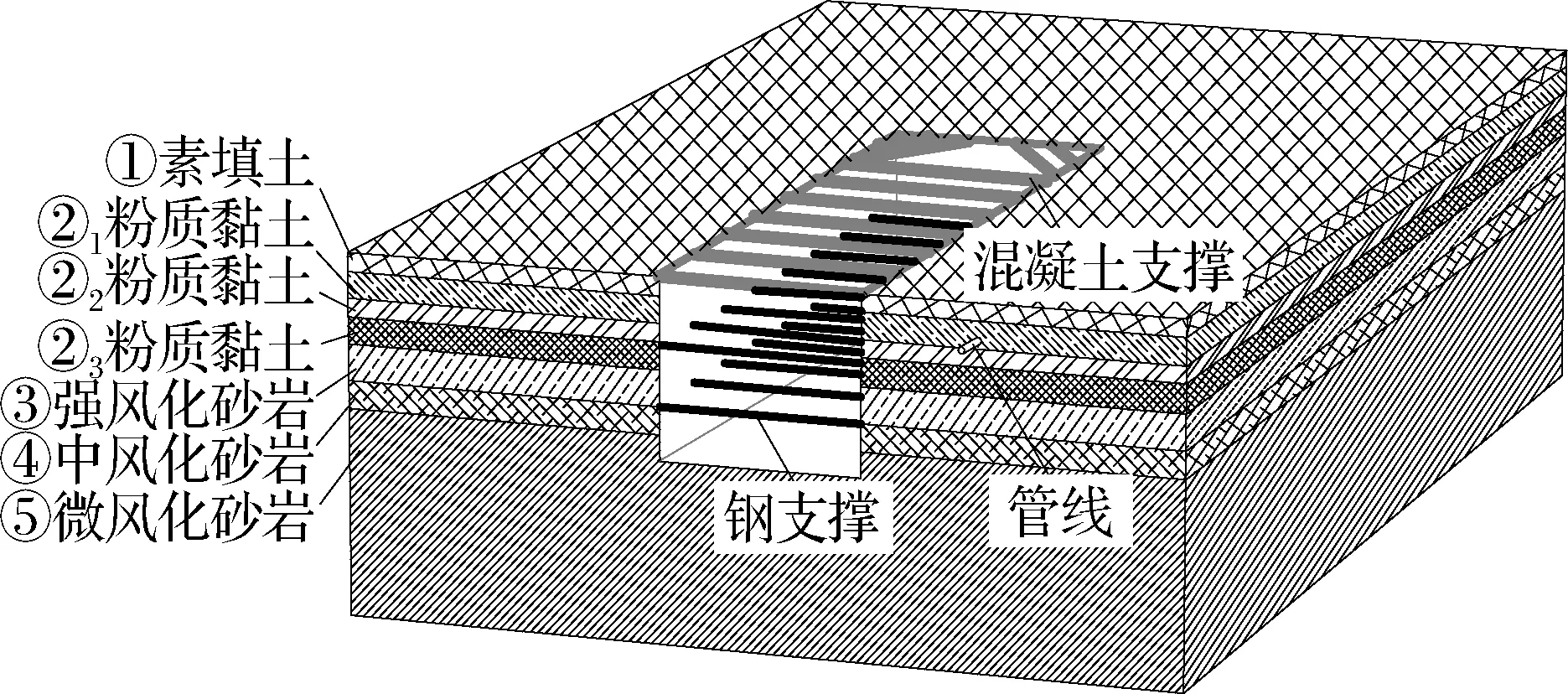
图5 基坑及管线三维模型
3.2 数值模拟与实测结果对比验证
图6为数值模拟计算出的地表沉降云图.由图可知,地表沉降最大值位于基坑长边两侧距基坑一定距离处,短边一侧地表沉降最大值即位于距基坑一定距离处,但地表沉降最大值要小于长边两侧的地表沉降最大值,基坑阴角处的沉降明显相对较小.
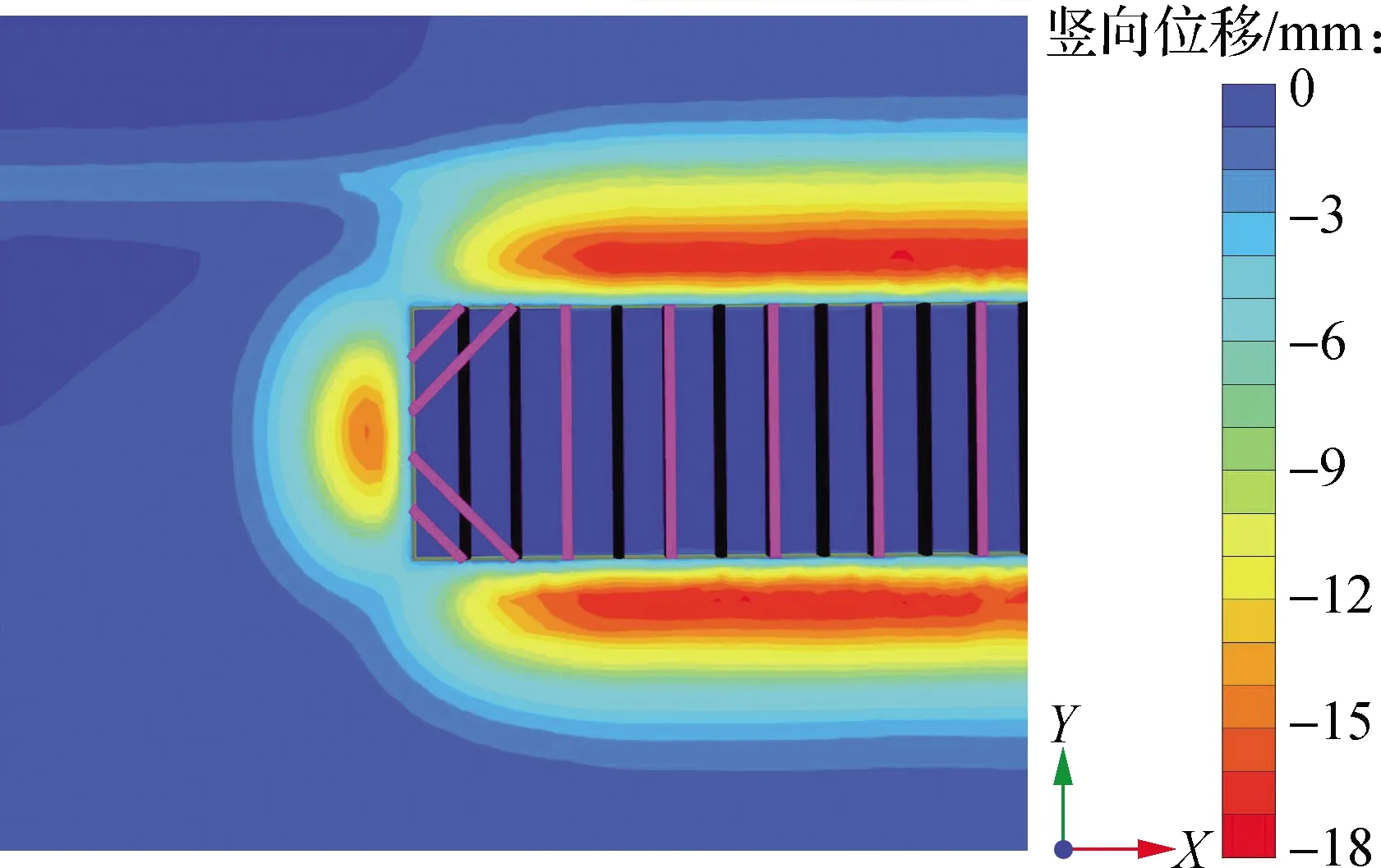
图6 地表沉降云图
将管线沉降监测点位B01~B10的数值模拟结果与现场实测值进行对比,结果见图7.由图可知,随着距基坑短边水平距离的增大,管线沉降的实测值和数值模拟计算值均逐渐增大,实测值与计算值总体相差不大.距基坑短边10~30 m水平距离范围内管线的沉降量计算值均略大于实测值,即计算值中管线的不均匀沉降现象相对更为明显.总体而言,计算值与实测值变化规律基本一致,从而验证了数值模型的可靠性.
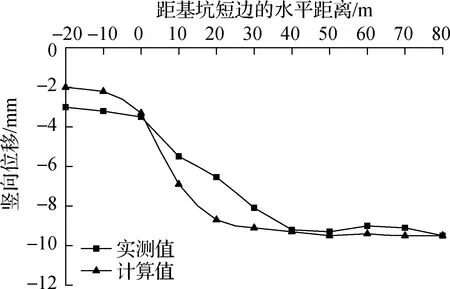
图7 DN1200污水管的数值模拟与现场实测数据对比
3.3 单因素数值模拟分析
针对基坑开挖深度、管线埋深和管线与基坑间距3个因素进行单因素数值模拟.每个因素取5~6个水平,以管线竖向位移和水平位移为评价指标,对比分析其对管线变形的影响.根据数值模拟结果,以基坑西侧端部为横坐标原点,基坑长边方向为横坐标,竖向、水平位移为纵坐标,绘制管线位移变化曲线图.规定距基坑短边的水平距离沿基坑内侧方向为正,外侧方向为负; 管线沉降为负,隆起为正;向基坑内侧的水平位移为正,外侧为负.
3.3.1 基坑开挖深度
基坑开挖深度取5、10、15、20、25 m五个水平,分别针对各工况进行数值模拟,对比分析管线竖向位移和水平位移.图8为不同开挖深度时管线竖向位移和水平位移随距基坑短边水平距离的变化曲线.
由图8(a)可知,随着基坑开挖深度的增大,管线沉降逐渐增大,但基坑西侧端部坑外部分基本不变,距基坑短边0~30 m水平距离范围内管线的竖向位移变化较大,产生的不均匀沉降较大,可能会对管线造成撕扯、拉裂,因此应对该区域管线加以特别保护,这与实测数据分析结果基本一致.在基坑中部距基坑短边30~80 m水平距离范围内管线的竖向位移基本相同,管线最大竖向位移发生在此范围内.
由图8(b)可见,管线水平位移变化规律与竖向位移基本一致,在距基坑短边30~80 m水平距离范围内管线水平位移大小基本相同,而在基坑端角部管线水平位移变化差距较大,在水平位移与竖向位移的共同作用下管线会加速破坏.因此,应对此区域管线予以特别保护.
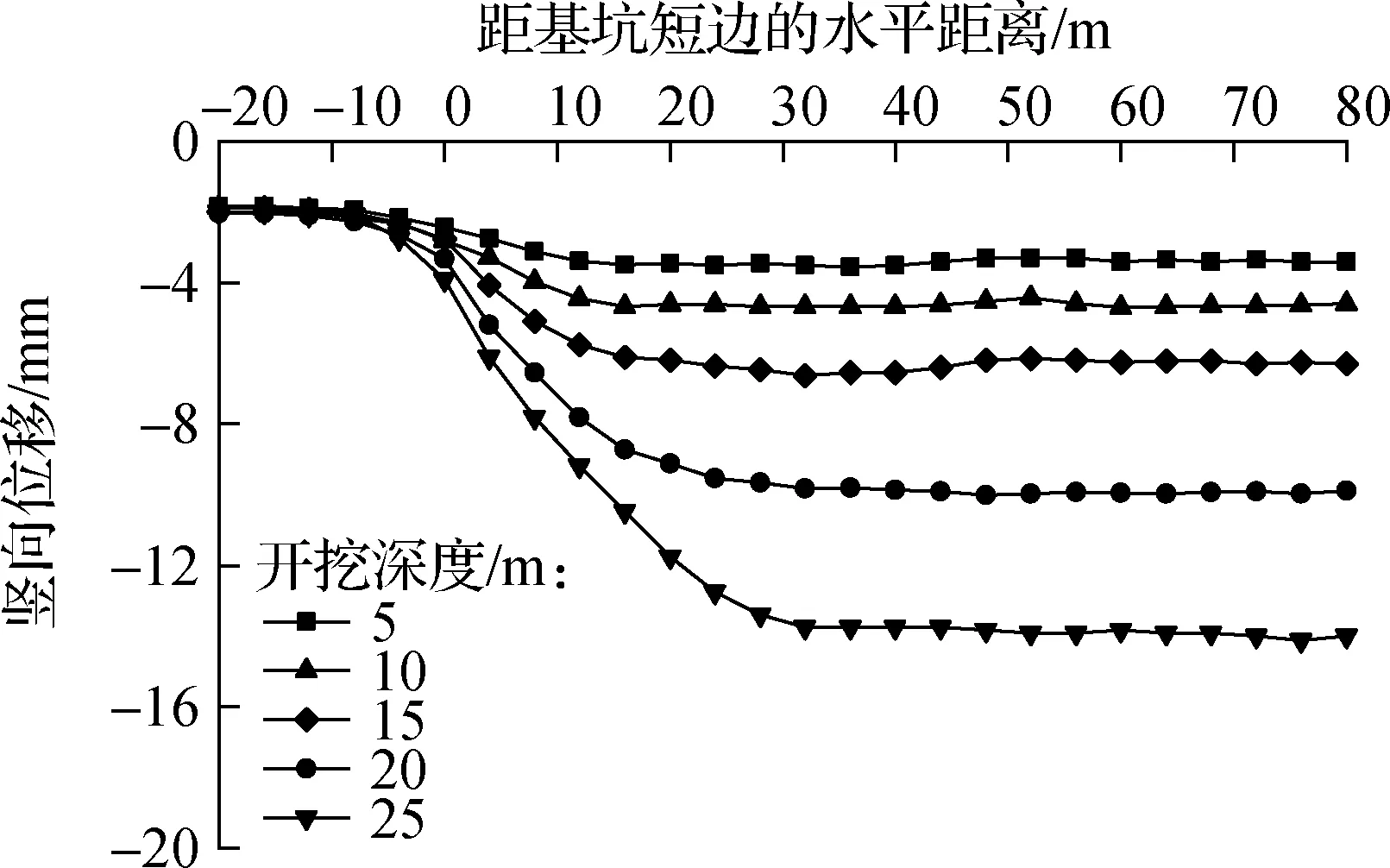
(a)竖向位移
3.3.2 管线与基坑间距
根据数值模拟试算结果可知,基坑开挖对坑外地表沉降影响范围为22 m左右.考虑到本工程管线与基坑间距为12 m,因此管线与基坑的间距在0.4~1.2倍基坑开挖深度中取值, 取8、12、16、20、24 m五个水平进行数值模拟.
图9为根据数值模拟结果绘制的不同管线与基坑间距下管线的竖向位移和水平位移对比图.由图9(a)可知,当管线与基坑间距大于16 m时,随着距基坑短边水平距离的增大,管线竖向位移大小基本不变,说明此时管线的不均匀竖向位移较小,对管线变形影响较小.当管线与基坑间距小于16 m时,管线竖向位移在基坑端部发生较明显的突变,产生较大的不均匀竖向位移,可能会对管线造成拉裂破坏.由图9(b)可以看出,管线水平位移变化规律与竖向位移基本一致.当管线与基坑间距小于16 m时,产生较大的不均匀位移,对管线的完整性产生较大影响.因此,当管线与基坑间距大于0.8倍基坑开挖深度时,管线不均匀位移较小,基坑开挖对管线的完整性影响较小.
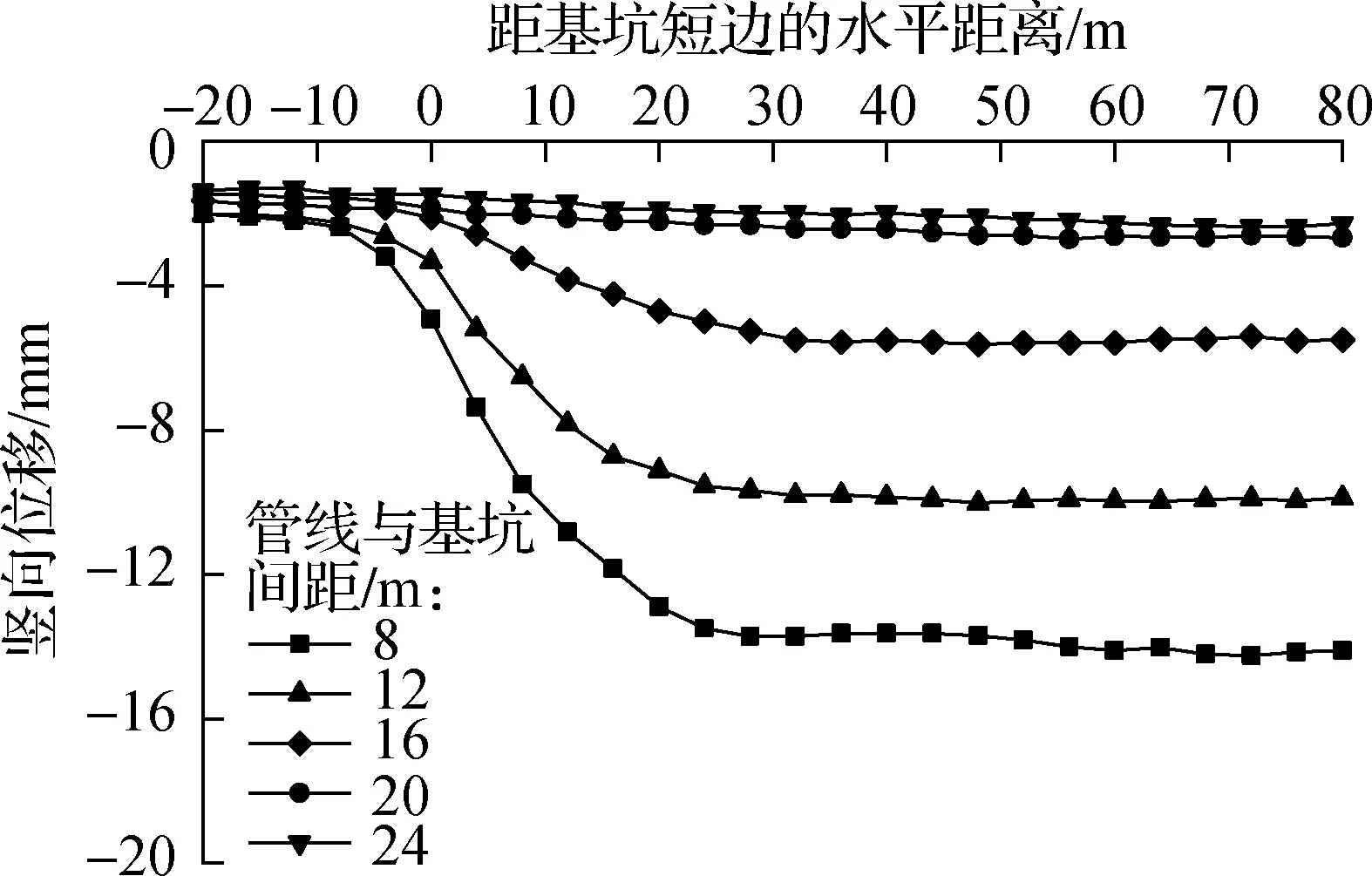
(a)竖向位移
由此可知,当管线与基坑间距大于0.8倍基坑开挖深度时,基坑开挖对管线变形的影响较小.
3.3.3 管线埋深
管线埋深是管线变形的主要影响因素之一.考虑到本工程管线埋深为3 m,管线埋深取1、2、3、4、5 m,分别针对这5种工况进行数值模拟.
图10为根据数值模拟结果绘制的不同管线埋深时管线的竖向位移和水平位移对比图.由图10(a)可看出,管线竖向不均匀位移主要发生在基坑端部0~30 m范围内,并且随着管线埋深的增大,管线竖向不均匀位移逐渐变小.当管线埋深为1 m时,管线的不均匀位移最大.由图10(b)可知,管线水平位移与管线竖向位移变化规律基本一致,当管线埋深为1 m时,管线的不均匀水平位移最大,发生在基坑端部0~30 m范围内.因此,为保证管线的完整性,防止管线发生不均匀位移而对管线产生破坏,管线埋深应不小于2 m.
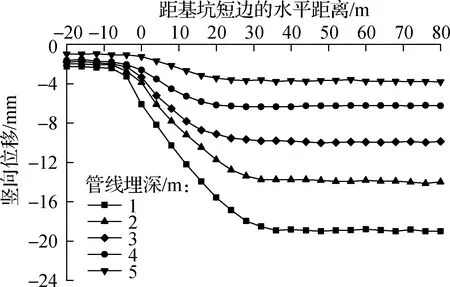
(a)竖向位移
4 不同参数的敏感度分析
为定量分析管线与基坑间距、管线埋深、基坑开挖深度3个因素对管线变形的影响程度,采用相对敏感度分析法进行对比研究.
敏感性系数ηSR为输出结果变化率与输入变量变化率的比值,即
(1)
式中,x和xLR分别为输入变量参考值和变化值;f(x)和f(xLR)分别为x和xLR对应的输出结果.
敏感度ηSS的计算公式为
(2)
式中,max(xR)、min(xR)分别为参数变化取值的最大值和最小值.
通过将变化量值归一化,可以将不同的敏感比进行无量纲化的比重衡量.表3给出了各因素对管线位移的敏感度.由表可知,对管线竖向位移和水平位移的敏感度由大到小均依次为管线与基坑间距、管线埋深、基坑开挖深度.管线与基坑间距对管线竖向位移的影响小于水平位移;管线埋深对管线竖向位移的影响大于水平位移;基坑开挖深度对两者的影响基本相当.
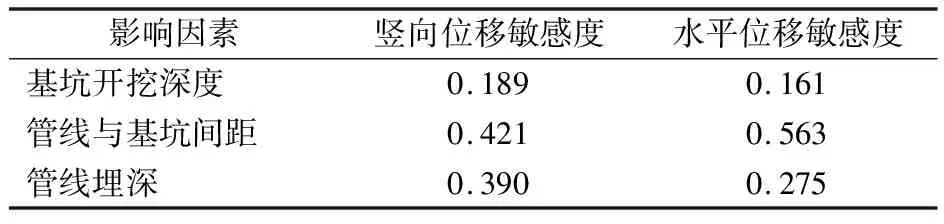
表3 各因素对管线位移的敏感度
由此可知,在土岩复合地层中进行基坑开挖时,管线与基坑间距对管线变形的影响最大,管线埋深次之,基坑开挖深度影响相对较小.在基坑设计过程中应首先考虑基坑与管线的水平距离,其次在考虑施工成本的基础上应尽量深埋管线.
5 结论
1)基坑开挖完成后,管线最终呈现出中间沉降大、两头沉降小的凹槽形,管线不均匀位移主要发生在基坑端角部20%开挖长度范围内.建议在基坑开挖前应对基坑端角部的管线加以特别保护,以避免不均匀沉降对该处管线造成拉裂破坏.
2)随着基坑开挖深度的增大,管线竖向位移和水平位移均逐渐增大,且管线竖向位移增加幅度相对较大.与单一土层相比,在上土下岩的土岩复合地层中进行基坑开挖对邻近管线的沉降变形影响相对较小.
3)随着管线与基坑间距的增大,管线竖向位移和水平位移均逐渐减小.当管线与基坑的间距小于0.8倍基坑开挖深度时,管线不均匀位移较大.
4)管线竖向和水平位移均随管线埋深的增大而逐渐减小.为防止基坑开挖对管线产生较大的不均匀位移而对管线形成破坏,管线埋深应不小于2 m.
5)通过参数敏感性分析可知,在土岩复合地层中进行基坑开挖时,管线与基坑间距对管线变形影响最大,管线埋深次之,基坑开挖深度对管线变形影响相对较小.
