制造冲突 启迪思维
2022-04-16山东教育社乔汝霞
山东教育社 乔汝霞
1 引言
矛盾是一切事物发展的动力,而认知冲突就是学生思维和能力不断发展的内在源泉.所谓认知冲突是一个人已建立的认知结构与当前的学习情境之间暂时的矛盾和冲突,是已有知识和经验与新知识之间存在某种差距而导致的心理失衡[1].它能够非常有效地刺激学生的求知欲,不断引发学生学习的内在驱动力,点亮学生积极思维的火花.对于数学这门学科而言,在课堂教学中制造有效的认知冲突,能让课堂更精彩纷呈,让学生思维更活跃,充分展示自我.
2 在新旧知识的矛盾中引发冲突
新知往往是在旧知的基础上衍生与发展的.学生已有的认知和经验是学习新知识的基础,当学生头脑中已有的知识不能解释新知识,与新知识发生矛盾时,心理上就会产生失衡,这时需要教师进行有效地引导,寻找新旧知识间的平衡点,这种寻找平衡点的过程就能引发学生知识产生的内驱力.利用已有的知识不断制造冲突,利用有创造性的问题使学生不断地处于探索之中,把学生置于矛盾中,让矛盾不断推动学生思维的发展,从而使学生产生要解决矛盾的迫切心理,进而进行更有效的学习.
我们先看下面的教学片段:
在学生自主完成问题解答后,分享解法时,却出现了下面的两种解法:

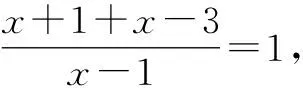
所以2=1.

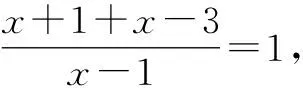
所以2(x-1)=x-1.
解得x=1.
面对两种截然不同的答案,学生十分迷茫.学生认为解法1每一步都是对的,但最后的结论不可理解.对此教师要引导学生分析两种解法每一步的依据和限制条件,看是否有错误,同时点拨提醒学生:分式约分的前提条件是x≠1,既然最后2=1不成立,说明原方程没有实数解(学生第一次接触没有实数解的方程,会感觉不可思议).
这时,有学生提出:既然解法1没有问题,那说明解法2是错误的.但大家一致认为解法2的每一步同样都没有问题.抓住学生这个矛盾冲突点,教师再次提醒学生:解法2中去分母的前提条件是x-1≠0,即必须满足x≠1,而最后的结果却恰恰是x=1,与限制条件矛盾,这说明x=1不是原方程的解,从而引出分式方程产生增根的原因,并再次说明解分式方程验根的必要性.
3 在学生的认知差异中激发冲突
不同的学生之间存在认知差异,因为每个孩子的智力水平不同,原有的认知结构不同,所以对新学的知识在认知上存在差异,他们之间的认知差异就会产生矛盾,思维的碰撞就会擦出火花.不同认知水平的学生对同一问题的不同认识,就会使得知识在探究的过程中更全面更完善,进而形成新的知识系统.
请看下面的教学片段:
由于学生们认知有差异,所以在操作时会出现各种不同的情况,这时教师要引导学生进行小组讨论,对所画情况进行归纳总结.
大多数学生会画出第二种(如图2)情况,通过不同知识结构的学生进行完善交流,会把三种情况(如图1、图2、图3)归纳总结出来.
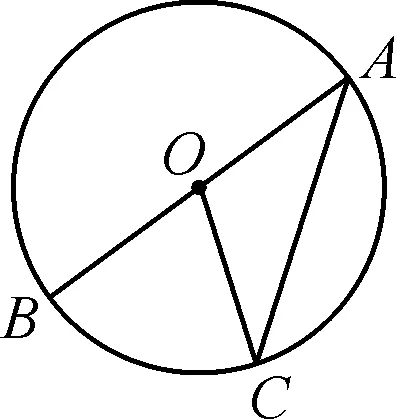
图1

图2

图3
师:若按圆心O与这个圆周角的位置关系来分类,我们可以分成以上三类.同一条弧所对的圆心角和圆周角的度数与什么有关系?动手量一量,∠BOC与∠BAC有何数量关系?
通过测量,可以发现∠BOC=2∠BAC,并且大胆猜想:同一段弧所对的圆周角等于它所对的圆心角的一半.
先引导学生大胆猜想,然后引导学生对以上三种情况进行证明.
(1)首先考虑一种特殊情况(如图1):当圆心O在圆周角∠BAC的一边AB上时,圆周角∠BAC与圆心角∠BOC的大小关系会怎样?
∵∠BOC是△ACO的外角,
∴∠BOC=∠C+∠A.
∵OA=OC,
∴∠A=∠C.
∴∠BOC=2∠A.

(2)当圆心O在圆周角∠BAC的内部时,圆周角∠BAC与圆心角∠BOC的大小关系会怎样?
师引导:是否能转化为第一种情况解决?
如图4,过点A作直径AD.
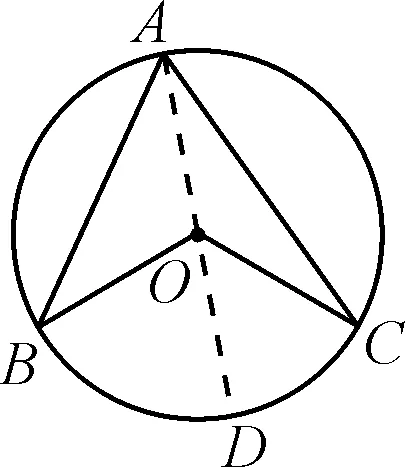
图4
由上述(1)的结论可得

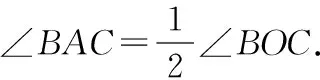
(3)当圆心O在圆周角∠BAC的外部时,圆周角∠BAC与圆心角∠BOC的大小关系会怎样?
师引导:同样考虑是否可以转化为第一种情况解决?
如图5,过点A作直径AD.

图5
由上述(1)的结论可得



进而可得圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
对于上述第一种情况,由于相对比较简单,大多数学生都能给予证明.但是第二和第三种情况的难点在于作辅助线将第二和第三种情况转化为第一种情况,运用转化的思想解决这类问题.由于学生存在认知差异,在解决这类问题时会出现认知冲突.此时,教师应当引导不同学习能力的学生解决不同层次的问题,这样尊重了学生认知水平的差异化,使不同的学生在课堂中都能得到能力的展示,实现分层教学,然后将所有的情况进行概括总结,完善成为新的知识系统.学生能在这种认知冲突中启迪思维,开阔眼界,形成严谨的数学思维习惯.
4 在师生互动交流中创造冲突
师生、生生的互动构成了整个课堂,要在课堂中借用学生认知冲突来形成有效交流;要使用有引导性的教学设计构建良性交流,以提高学生的自主探究和归纳总结的能力,不断提高课堂效率.教师必须要学习先进的教学理念,借助高效的教学手段,形成良性和谐的师生交流互动,确保教育教学效果得到进一步提升[2].
请看以下教学片段:
师:任意的三条线段都能围成三角形吗?构成三角形的三条边的长度之间有什么规律呢?
通过问题的出示引导学生从对 “三角形有三条边”的初浅认识,进入到对三角形三边关系的探究中来.
4.1 初步感知规律
(1)各小组准备好表1所示的记录单和四根下面长度的小棒,其中2 cm,4 cm,6 cm,8 cm小棒各1根.
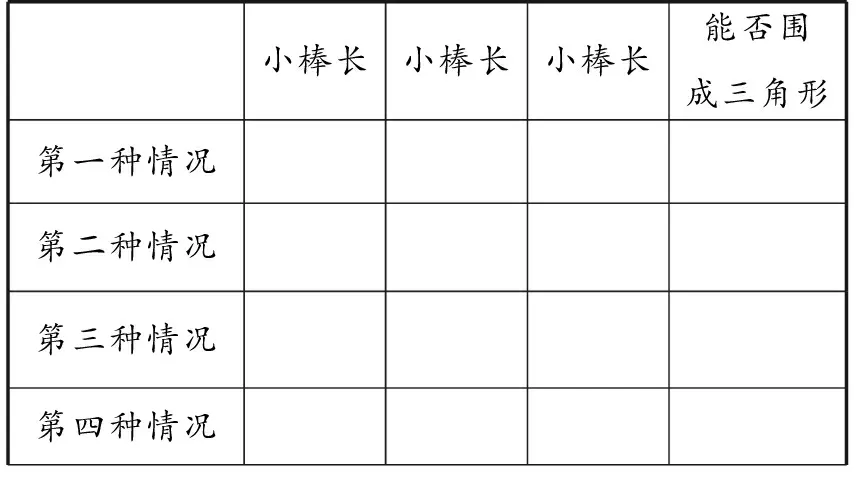
表1 (单位:cm)
(2)大屏幕出示要求:
①小组合作,组长合理安排操作和填写实验记录单;
②操作过程要遵循秩序,并记录所有可能出现的情况;
(3)学生进行操作,教师要不断进行巡视;
(4)分组选派代表进行汇报,并展示学生汇总结果.
师:为什么有的情况不能围成三角形?可能与什么有关?
本环节让学生进行小组讨论,整个小组成员参与其中,手脑并用,让每个学生都亲身经历实验的全过程.通过操作、观察、交流、归纳的过程,引导学生进行大胆猜想,迈出探究规律的第一步.
4.2 分析、探究规律
(1)发现规律.
师:哪种情况下,三根小棒不能围成三角形?
小组内利用小棒进行实验操作,教师进一步追问:它们为什么不能围成三角形?
小组合作交流,由学生代表上台展示,并发现:
三根小棒中,任意两根小棒长度的和等于或小于第三根小棒的长度时,这三根小棒不能围成三角形.
其他学生做补充与质疑.
(2)验证规律.
师:①怎样的三条线段才能围成三角形呢?
②能围成三角形的三条线段中,任意两条线段的长度和都大于第三条线段的长度吗?
请学生独立完成,从能围成三角形的两种情况中,任选一种进行计算验证,这样可以节约时间,计算完毕后小组汇总所有情况,并进行汇报展示.
(3)揭示规律.
师:构成三角形的三边的长度具有怎样的关系呢?
师生共同归纳总结,并板书:三角形任意两边之和大于第三边.
5 总结
在教学设计中,教师要多设计动手实践环节,不断地进行实验操作.通过直观的实验操作的过程,引导学生自主发现规律,并且不断地追问,再让学生通过计算从正面验证规律,最后,水到渠成地揭示规律.在整个教学活动中,不断创造师生、生生的认知冲突,让学生亲身经历知识形成的过程,丰富数学实践活动的经验,并在自主发现、验证、概括的过程中,体会数学的科学性、严谨性,获得成功的学习体验[3].
在数学教学中,我们要不断地制造冲突.在新旧知识的矛盾中引发冲突,在学生的认知差异中激发冲突,在师生互动交流中创造冲突,让冲突贯穿于整个教学活动.当然,如何制造冲突成为教学设计的关键.教师要不断更新观念,提高自身能力,让数学课堂成为启迪学生思维的殿堂,让学生全方位参与到知识的形成中来,真正提高学生的数学能力.
