基于最优尺度下的黄土高原区小流域密度及分形规律

王泽远，马良哲，杨飞翔

（1.陕西地建土地勘测规划设计院有限责任公司,陕西 西安 710075；2.中国冶金地质总局中南局,湖北 武汉 430034）

0 引言

栅格数字高程模型（DEM）固有的尺度特征给以栅格DEM为基本输入的数字地形分析带来各种尺度问题,由于分辨率及遥感产品的选择不同,DEM对地表信息的刻画的精细程度也存在着显著的差异性[1]。李小文院士在研究中给出尺度效应较为通俗的解释,指在某一尺度上观测到的性质、总结出的原理或规律,在另一尺度上可能仍然有效,也可能相似或者需要修正[2],因此选择合适的尺度分析地形信息是尤为重要的。甘肃陇东黄土高原地区的水土流失及水力侵蚀作用强烈,沟谷形态复杂,沟道密度和分形特征可以很好地刻画出沟谷整体的形态特征。沟道密度反映出沟道网络的疏密程度,分形特征反映出沟道细枝末节的复杂程度,一般来说,分型维度值越大,其具有的自相似性就越高,说明物体在一定空间内延伸出的小分支越多,复杂程度越高[3]。在目前的研究中,多在特定DEM尺度下讨论沟谷的形态信息,鲜有考虑尺度效应下沟道密度及分形维数的特征,以此研究,可以排除尺度效应对地形信息的干扰,从沟谷系统整体性质上,分析沟谷的形态特征,得出演化规律,为黄土高原区沟谷形态演化研究提供更为可靠的科学依据。

1 研究区概况

纸坊沟流域地处于陇东平凉市崆峒区的城南,发源于虎狼山,位于泾河上游的右岸,为渭河一级支流泾河的二级支沟。纸坊沟的流域面积较小,仅19.05 km2,但其与城市中心距离仅有5 km,治理难度大,危害较高。属于较为典型黄土高原地区泥流沟,是最早被列入重点治理的流域。纸坊沟所属的崆峒区是平凉市的行政区,位于甘肃省的东部地区,六盘山东部。西边接壤宁夏自治区的泾源县,东部与该市区的泾川县和庆阳市接壤,交通网络十分便利。

2 数据来源及研究方法

本文以不同时空尺度为背景,结合GIS与分形理论,从各尺度范围中选择研究陇东黄土高原区小流域沟道密度及形态的最优尺度,并横向分析最优尺度下各年份流域密度和分性特征的演化趋势。最后计算流域上、中、下游内共18个小流域的密度及分形维数值,分析两者之间的相关性。

2.1 数据来源

2000 年的DEM数据来源于DLR的SRTM数据,数据精度为30 m。

2009 年DEM数据来源于由美国国家航空航天局（NASA）发布的先进星载热发射和反射辐射仪全球数字高程模型（ASTER GDEM）,数据精度为30 m。

本文利用ENVI软件从2019 年资源三号遥感卫星中的立体像对数据里进行手动提取2019 年DEM数据。

2.2 研究方法

2.2.1 尺度效应

本文使用ENVI4.1软件创建2.1 m×2.1 m～420 m×420 m共15 个不同尺度的DEM,通过空间链接建立新的图层。随着分辨率尺度变化,地表反应信息由碎片化向整体逐渐过渡。

2.2.2 沟道密度

沟道密度是流域内地表面每一公里范围内侵蚀沟系的总长度,是表示地质营力对地表侵蚀影响的重要条件。

采用的汇流累积量阈值设置分别为100、200、300、400、500、600、700……3000,利用GIS软件提取出与之相对应的沟道网络[4],最终确定最佳的汇流累积量,手动操作选择边缘很短的平行状态通道作为伪通道进行删除。

统计不同汇流累积量阈值下的沟谷长度,计算对应的沟道密度,沟道密度是指单位面积内沟道的总长度,单位为km/km2,其表达式为[5]：

式中：D代表沟道密度；L为沟道长度,km；A指研究区面积,km2。

2.2.3 分形分维数

李小文[6]等认为不同尺度之间存在“相似性”或“自相似性”的关系,即不同尺度之间由于像元大小和地表复杂程度不同,可以表达为分形的关系,对应的定量参数是分形维数,采用计盒维数法计算。

计盒维数法的计算思路是使用不同边长r的正方形盒子去嵌套被测量的河道网络,河道网络中会存在不同尺度的空间,会有未被盒子所覆盖的沟道碎片,将非空盒子数目（包含有沟道片段的盒子数量）记为N（r）,不断改变半径r,会出现不同嵌套数量的盒子数N（r）,r和N（r）呈反比,当r无限趋近于0时,可以近似得到沟谷网络的分形维数计算公式[7]：

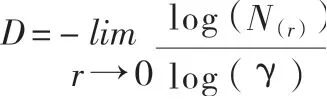
2.2.4 均值变点法

在本文中,均值变化点法用于计算沟长最佳分辨率。均值变化点分析方法是用于处理非线性数据的数学统计方法,该方法对于只有一个变化点（拐点）的测试最为有效[8]。计算公式如下：

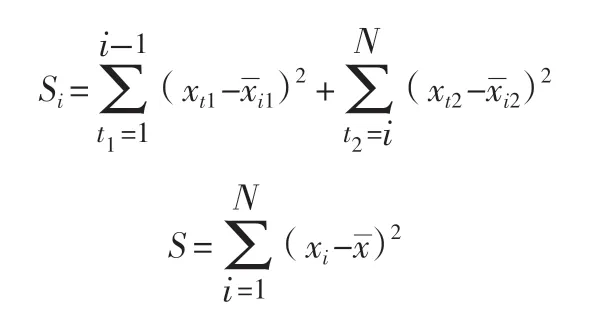
式中：下脚标t1=1,2,…,i-1；t2=i,i+1,…,N,变点使得S和Si的差距增大,两者最大差值对应点为变点。

3 研究结果

3.1 沟道密度的分形尺度效应

考虑到不同分辨率DEM数据获得的最佳汇流面积阈值不同,为了在同一阈值下对多个DEM数据提取的沟谷进行比较,本研究以2019 年DEM数据为标准,按照沟道密度提取方法,求出最佳汇流面积阈值,对其他尺度和年份的数据进行计算时,采用该阈值,以保持统一性。绘制出2019 年沟道密度与汇流累积量阈值的拟合曲线关系图,见图1、图2。

图1 不同阈值与沟道密度相关性图

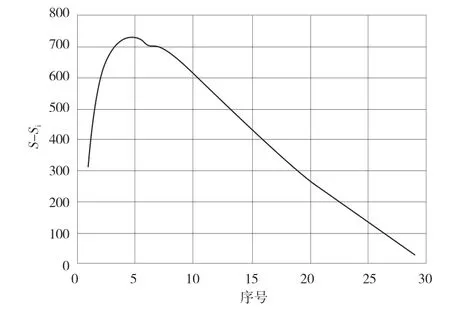
图2 均值变点法

由图1、图2可以看出,汇流累积量阈值与沟道密度之间呈现出幂函数关系,且R2为0.9883,说明拟合程度较好,在汇流累积量阈值小于500的范围内,降低的幅度最大,而后逐渐趋于平缓,且S与Si的差值达到最大值,为727.98。故本文采用500 汇流累计量阈值对其他尺度及年份数据进行计算。

使用ENVI4.0软件,从2019 年立体像对影像中按照2.1 m×2.1 m～420 m×420 m每隔30 m分辨率提取共15 个不同尺度的DEM。以汇流累积量500 分别提取流域沟道网络,随着尺度范围不断增大,沟谷网络数量明显减小,沟谷长度随之降低,并使用TopoToolbox 2.0 程序依次计算沟道密度。见图3。

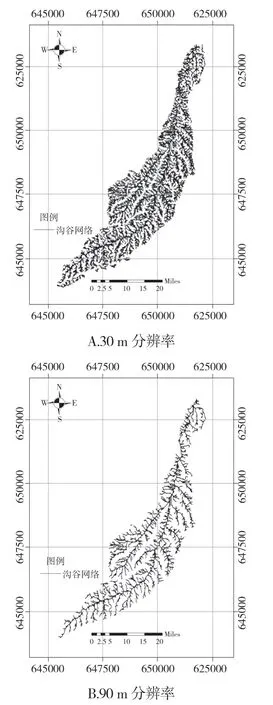
图3 不同尺度范围下提取的沟网

由图4可以看出,当分辨率不断增大,由于地表信息有破碎向整体过渡,细小的次级沟道随着分辨率的增大而消失,沟谷长度总量减小。随着分辨率尺度增加,DEM精度降低,短小的沟道难以被识别出来,直接导致沟道长度最大值、最小值和平均值的增加。沟谷长度值在分辨率90 m之前的变化速率较高,总体减少46%,每隔30m尺度平均减少15.3%,分辨率90 m之后,每隔30 m尺度平均减少仅为2.8%。根据流域沟道密度计算公式,沟道密度与沟道总长度具有正相关关系,变化趋势相同,90m分辨率为变化速率由陡向缓过渡的拐点。

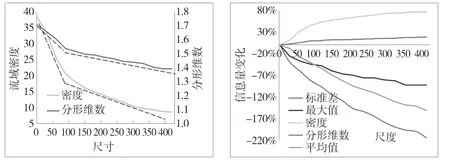
图4 信息变化与损失量图

损失率是指在DEM分辨率变化的过程中,统计值相较于原始值的损失情况,可以从侧面反映出数据精度下降对数据测量带来的影响[9]。沟道长度最大值累计损失量为-92%,平均值累计损失量为-151%,标准差为-214%。该特点反映出,当分辨尺度变大,大量范围的沟道在测量时会被平均化处理,分辨率越高,地形量测信息越为准确,沟长值区间跨度越高。沟谷网络具有明显的尺度效应敏感性。当分辨率达到90 m之后,各沟谷信息值变化趋势降低,曲线逐渐过渡至平缓,尺度效应逐渐消失。由此可见,90 m分辨率DEM数据为反应沟谷长度等信息量的最优尺度。

3.2 沟道密度及分形的时空效应

3.2.1 沟道密度变化

上文通过分析不同分辨率提取沟道的变化趋势,得出90 m分辨率为研究沟道密度的最优分辨率,本节以90 m分辨率DEM为基础资料,按阈值为500 提取出三个研究年份的沟谷网络,按照集水面积的大小将流域划分为上中下三段,并计算沟道密度[10],得出流域密度空间分布图,见图5。

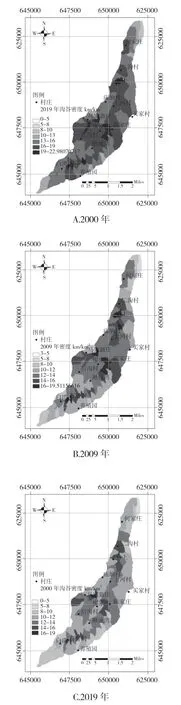
图5 2000年、2009年、2019年沟道密度分布图（右）

经过计算,纸坊沟2000年沟道密度为12.39 km/km2；2009年沟道密度为13.97 km/km2；2019年沟道密度为15.84 km/km2,20 年间增长13.38%。2000年～2019年沟道密度结构普遍由较低密度往较高密度过度。

上游的沟道密度最低,2000年仅为7.92 km/km2,2019 年增长至9.65 km/km2,增长率为21.8%。纸坊沟沟谷仍处于发育时期,沟坡稳定性较低,由于经历了长时间的侵蚀作用,变得相对稳定,虽然也有少量侵蚀发生,但总体占比较低,所以上游近20 年沟道密度变化较低。中游高密度区域在沟谷中游分布较为广泛,并且呈现出逐年增加的趋势,从2000年的12.28 km/km2,增加至2019 年的14.97 km/km2,增长率21.9%。下游沟道密度从2000 年的8.51 km/km2增长至2019 年的10.13 km/km2,增长率为19%。由于下游地势较为平缓,山谷起伏较低,并没有出现垄岗起伏,坎坷不平的地形,受到水流的侵蚀作用较弱,沟道密度的变化也最慢。

3.2.2 分形分维值变化

一般来说,分形维度值越大,其具有的自相似性就越高,说明物体在一定空间内延伸出的小分支越多,形态更具有复杂性[11]。伴随着沟道发育程度的不断增加,沟道形态结构的复杂程度越大,沟道网络所表现出来的自相似性也越来越高。因此,通过分形维数可以很好地表达沟谷的空间展布特征与沟谷形态特征。

将三个年份分流域内统计得到的r与N（r）值,分别取对数,求出拟合直线。直线斜率即为分形维数D。拟合曲线关系见图6。

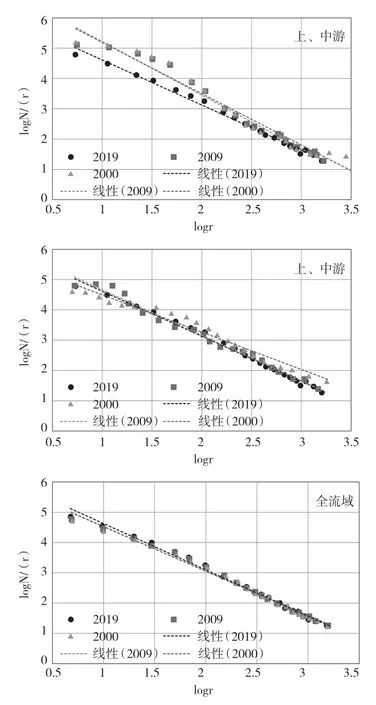
图6 2019年上、中、下游分形分维值

依据上述方法依次计算可知,分形维数拟合方程的相关系数较高,均在0.99以上,分形维数出现随年份持续增大,上游增大7%,上、中游增大8.3%,全流域增大4.5%。沟道的发育会促进支沟的不断发育,侵蚀沟道两侧坡面,改变地貌景观,在2000 年,纸坊沟地表切割深度较小,支沟短小而且数目较少,沟道分维值相对较低。受地质灾害的影响下,纸坊沟内的地形结构经常处于变化过程中,主沟和支沟均会发生不同程度的侵蚀作用,造成沟系的复杂程度不断变化,发展至2019 年,分维值的增高,纸坊沟各地区的小沟道逐渐增多,但其表现出往稳定的结构过度中。

3.3 沟道密度与分形维数的相关性

水系分维数与区域沟道密度密度间也存在着一定的相关关系,水系分维数反映了水系结构的复杂程度,沟道密度代表了区域水系的疏密程度。一般沟道密度越高,沟谷内的支沟数量也越高,沟道展布延长,沟谷整体复杂程度增加。本文选取上、中、下游共18个二级支沟,分别计算其沟道密度与分形维数。

由图7、图8可知,流域上中下游沟道密度与分形维数均呈现出正相关性,随着沟道密度值得升高,分形分维值也随之增加。上游侵蚀切沟较为发育,相关性值处于（1.4,11）～（1.6,15）之间,值域最大。中游相关性值跨度较大,拟合趋势线R2为0.78,说明分形维数与沟道密度之间的相关性高。下游沟谷地势较为平缓,值域范围最窄,且处于较低范围内。由分形维数—沟道密度图可以得出,纸坊沟流域分形值在（1.3～1.4）,沟道密度值在（7～9）之间的二级支沟数量最多,分布密度在0.6以上。由此可知,纸坊沟流域沟道结构的复杂程度与沟道结构的疏密程度是相一致的,沟道密度越高,沟道自相似性越大。

4 结论

基于尺度效应的分析,得出研究陇东黄土高原地区沟道特征的最优尺度。对比分析流域20 年过程中沟道密度及分形的演化趋势,最后讨论沟道密度与分形维数的相关性,得出：

（1）陇东黄土高原小流域对于水系疏密及复杂程度的最优表达尺度为90 m分辨率。

（2）纸坊沟2019年沟道密度密度值最高,为15.84 km/km2,相较于2000 年增长13.8%,沟道密度结构普遍由低密度区往高密度区过度,下游沟道密度最低,中游沟道密度最高,且均呈现逐年增加的趋势。分形分维值与沟道密度的变化方向一致。

（3）沟道密度与分形维数呈现正向相关性,说明小流域在演化发育时,沟道分布结构的密度越高,其复杂程度也越高。分形维数在（1.3～1.4）区间,沟道密度在（7～9）区间的小流域分布最多。