基于SSA-DBSCAN的边坡安全监测数据粗差探测方法

蒋齐嘉，蒋中明，2，唐 栋，3，曾景明

(1.长沙理工大学 水利工程学院，长沙 410114； 2.水沙科学与水灾害防治湖南省重点实验室，长沙 410114；3.洞庭湖水环境治理与生态修复湖南省重点实验室,长沙 410114)

1 研究背景

随着对自然资源的开发与利用，近些年自然灾害的频次明显增加，工程领域相关的风险也随之增高，因此准确的安全监测变得尤为重要。显然安全可靠的监测数据是实施边坡安全监控的重要基础，更是后续正确分析预测的必备前提，但是监测数据的获取过程不可避免会受到人为失误、外界干扰、设备故障等因素的影响，因此监测数据中往往会出现少量异常的数据，这类异常数据即为粗差[1]。归根溯源可知，粗差其实是错误的数据，如果不及时处理会严重影响后续的分析预测，进而影响对边坡安全性的评判。因此，快速而又准确地识别监测数据中的粗差具有重要意义。

粗差的识别探测属于数据异常检测范畴，现阶段如何进行异常检测,可以归纳为统计学的方法、根据距离的方法以及聚类的方法等[2]。一方面现有的粗差探测方法往往只基于单一理论，在面对监测数据离群点较多或较小时，误判和漏判便随之出现[3];另一方面监测数据常呈现出非线性非平稳特点，若直接对原始数据应用上述探测法很难成功识别粗差。因此,为解决上述问题，诸多学者开展了相关研究。

蔡晓军等[4]采用多通道奇异谱分析(SSA)对全球导航卫星系统(GNSS)序列数据实现粗差探测。张东华等[5]针对沉降和大坝变形监测数据，提出了一种基于SSA与未确知滤波法(UF)的联合方法实现粗差探测。陈利军等[6]为提升电离层扰动数据分析准确性,剔除异常数据，提出了基于密度聚类算法(DBSCAN)的地震电离层扰动异常数据检测方法。罗怡澜等[7]根据某型机车履历数据，提出基于K-means与DBSCAN的联合异常检测模型。郑霞忠等[8]根据大坝位移监测数据，引入DBSCAN算法以识别大坝工作运行中的异常数据，王露[9]同样使用DBSACN算法对大坝温度监测数据进行异常检测。

鉴于此，本文引入SSA和DBSCAN算法。SSA在识别周期和趋势项上具有一定的优势，能够较准确的提取信号[10-11]。DBSCAN算法是基于密度的聚类算法，该方法成功解决K-means未能解决的不规则形状的聚类问题，同时该算法在区分异常值和粗差点上具有明显优势。

综上所述，本文基于这2种算法的特点提出了SSA-DBSCAN粗差探测法。通过引入边坡安全监测实例进行研究，对比分析了SSA-DBSCAN粗差探测法与其他常规传统方法对边坡监测数据的粗差探测效果，从而为后续的安全评价、变形预测、乃至滑坡预警奠定基础。

2 SSA与DBSCAN算法

2.1 SSA原理

SSA最初由Colebrook(1978)提出[12]，是一种适合非线性时间序列的研究方法，它根据时间序列建立轨迹矩阵并进行分解与重构，然后从中识别出周期信号、趋势信号和噪声信号[13]。SSA主要包括分解和重构2个步骤，对于一组长度为N的一维时间序列x1,x2,…,xN的SSA主要过程如下[14-15]。

建立轨迹矩阵X为

(1)

式中L为窗口长度(或称为嵌套空间维数)，1≤L≤N/2，一般通过适当方法或者经验拟定。然后对X进行奇异值分解，可得

(2)

(3)

分解后对所得的L个矩阵Xi(i=1,2,…,L)分组为

X=XI1+XI2+…+XIp。

(4)

式中任何一个XIi都是由一个或者多个Xi合成，并且不同的XIi内所包含的Xi不同。

将分组所得到的每个L×K矩阵XIi应用对角平均法转换为新重构序列RC(reconstruction),即

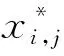
(6)

显然通过对角平均法，原始时间序列可以分解为p(1≤p≤L)个长度为N的时间序列之和[17]，p之后的分量视为噪声构成残差序列。

2.2 DBSCAN算法原理

DBSCAN算法是Ester等[18]在1996年提出的一种基于密度的聚类算法。该方法成功解决K-means未能解决的不规则形状的聚类问题，同时也对噪声数据处理较好，即该算法在识别数据集中任意形状的聚类的同时，更可以找出噪声。

DBSCAN算法的2个参数(Eps,MinPts)的设定很大程度决定聚类结果,其中,Eps表示邻域距离阈值，MinPts表示邻域范围内包含样本数目的临界值，即邻域密度阈值[19]。若数据集D=(x1,x2,…,xN)，DBSCAN算法关键定义如下[20]。

(1)核心对象：对于任一样本xj∈D，若其Eps邻域内至少包含MinPts个样本，则称xj为核心对象。

(2)密度直达：若xi位于xj的Eps邻域中，且xj是核心对象，则称xi由xj密度直达。

(3)密度可达：若存在数据集序列p1,p2,…，pT，满足p1=xi,pT=xj且pT+1由pT密度直达，则称xj由xi密度可达，即密度可达具有传递性。

(4)密度相连：若存在核心对象样本xk，可使xi和xj均由xk密度可达，则称xi和xj密度相连。

DBSCAN算法步骤简述如下[21]：①输入样本数据序列，设置参数Eps和MinPts，从序列中任选1个尚未处理的数据点x，然后对x进行核心对象的判别；②若x是核心对象，则找出数据序列中x对应的全部密度可达点，x与其构成一个新的簇；③根据簇中各点的密度相连关系得到一个聚类；④重复执行步骤②、步骤③，并对数据序列中所有的数据点进行处理，可得最终的聚类结果以及噪声数据。

3 基于SSA-DBSCAN的粗差探测法

3.1 SSA信号提取及可疑粗差拟定

本文使用SSA对含粗差的边坡监测数据进行信号提取和粗差位置的初步拟定。首先，根据监测数据序列长度，拟定合适的窗口长度L进行奇异谱分解;然后根据贡献率ci[5]及模极值点的情况，拟定参数p以得到重构序列和残余分量；接下来，结合原始监测信号对残余分量进行分析，通常来说残余分量中的模极值点可定性视为可疑粗差点[5]；最后，从数理统计角度出发定量的设置合理阈值，若残差绝对值大于该阈值，则视该点为可疑粗差点。

3.2 DBSCAN数据异常检测

边坡安全监测过程中异常数据的出现在所难免， 根据异常数据产生的原因， 异常数据可以归纳为边坡状态异常和边坡监测粗差2类。 边坡状态异常是指由于多方面原因边坡自身状态出现异常， 与粗差不同， 该类数据异常反映了边坡异常的自身状态， 研究过程中需将其准确识别提取并进行重点分析。

边坡监测粗差其实是由于人为因素、外界干扰，甚至是设备故障得到的错误数据，必须对其准确识别并剔除[8]。为了准确检测边坡安全监测数据，实现精准区分粗差和异常值，本文提出基于密度聚类的DBSCAN 算法检测边坡监测序列中的异常数据。

3.3 SSA-DBSCAN粗差准确探测

SSA算法在提取信号方面颇具优势，但是其在探测较小的粗差方面不够准确，而且在数据较多时容易出现误判[5]。DBSCAN算法是基于密度的聚类算法，该算法在实现区分粗差和异常值的同时还可以解决SSA不能探测较小粗差的局限性。但是该算法的调参相对于传统K-means之类的聚类算法更复杂，需要对Eps和MinPts联合调参；并且在聚类结果出现临界簇的情况下，难以直接判断临界簇的异常点是否为粗差。

综上所述，针对边坡安全监测数据，本文联合2种算法的优势提出了基于SSA-DBSCAN的粗差探测新方法，该方法简述如下：

(1)输入含粗差边坡监测数据，使用SSA提取信号并结合阈值拟定可疑粗差点。

(2)输入SSA提取的残余分量，使用DBSCAN算法进行异常检测，得到噪声和临界簇集合。

(3)将上述两步得到的可疑粗差点和临界簇集合进行对比然后取交集，准确识别出临界簇中的粗差。

(4)将步骤(2)中得到的噪声与步骤(1)中得到的可疑粗差点进行对比，再结合人工监测经验分析，以准确识别出噪声中的粗差。

(5)将步骤(3)和步骤(4)中得到的粗差合并，至此实现高效准确的粗差探测。

4 实例分析

4.1 边坡水平位移监测序列

采用三板溪水电站东岭信边坡DLXG01测点的水平位移监测序列为例(时间从2011年6月至2018年11月)，在2、12、13、17、21、138、139、163、164、172、173期数处随机加入大小不一的共计11个粗差，形成复杂的含粗差监测数据，如图1所示。

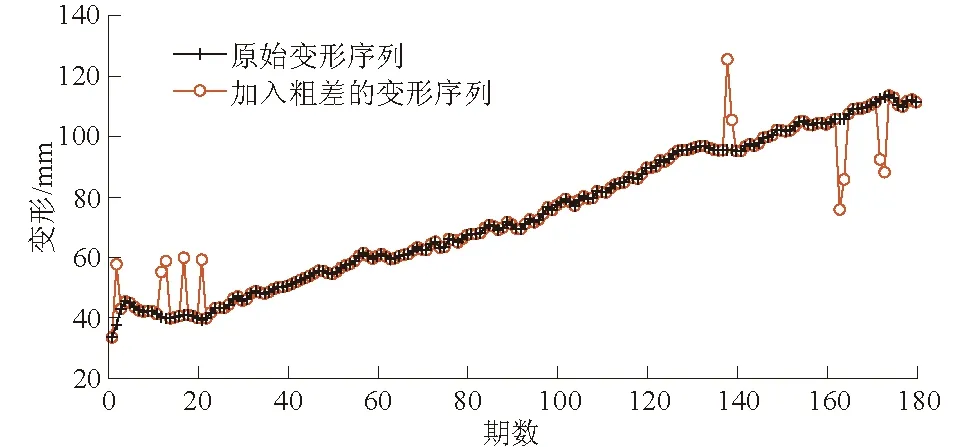
图1 位移观测数据序列Fig.1 Original displacement data series

首先输入含粗差的数据，应用SSA法。由于监测数据共180期(每期为15 d)，选取窗口长度L为90。目前重构信号分量的选取方法有很多，本文以贡献率ci为依据选取重构分量的个数[16]，试验结果显示：前3个重构分量的贡献率已经达到了99.8%，因此选取前3个分量重构监测序列，其余分量组成残余分量。SSA结果如图2所示。

图2 边坡变形序列SSA提取的重构信号及残余分量Fig.2 Reconstruction signals and residual componentsextracted from slope deformation series by SSA

从图2可看出残余分量在2、13、17、21、138、163、173处存在模极值点，然后定量计算残差序列的标准差获得阈值以进行可疑粗差点判别[5]，即当残差绝对值>2σ(2σ=9.197 2 mm)时判定该点为可疑粗差点，可得2、12、13、17、21、138、163、164、173、174为可疑粗差点。

然后，输入含粗差的数据，应用DBSCAN数据异常检测算法。值得注意的是，使用过程中需通过对Eps和MinPts 2大参数联合调参以获得最优结果，本文最终选取Eps和MinPts分别为3.9和3.0。

DBSCAN数据异常检测结果如图3所示。根据试验结果：1、138、139、163、164、172、173点为噪声点，2、12、13、17、21点构成临界簇A，177、178、179、180点构成临界簇B，其余点为正常数据。

图3 边坡变形序列DBSCAN异常检测结果Fig.3 Result of DBSCAN anomaly detection of slopedeformation series

接着，根据本文提出的SSA-DBSCAN粗差探测法，将SSA得到的可疑粗差点和DBSCAN得到的临界簇集合A、B分别进行对比并取交集，可得2、12、13、17、21为临界簇中的准确粗差。与此同时，根据异常值检测理论，通过DBSCAN得出的噪声均视为异常值，但由于1点在此前并未被识别为可疑粗差点，此时需要结合监测经验和边坡位移演变规律对其异常类别进行判别：由于该点为初始点并且此时边坡处于加速变形阶段，故判断该点并非粗差点。综上可得138、139、163、164、172、173为噪声中的准确粗差。

最后将2组准确粗差合并，结果如表1所示。至此成功探测出了全部11个粗差点，实现了对边坡位移监测数据的高效准确的粗差探测。

表1 边坡变形序列SSA-DBSCAN粗差探测结果Table 1 Result of gross error detection of slopedeformation series based on SSA-DBSCAN

为了验证该方法的优势，本文仍使用该边坡水平位移监测序列，采用中位数绝对偏差法(MAD)和格拉布斯准则法(Grubbs)进行对比验证，如表2所示。表2中TP为准确识别出的粗差个数，TN为准确识别出的正常点个数，Precision(精准率)为所有被探测为粗差的点中实际为粗差的个数比率，Recall(查全率)为所有实际为粗差的点中被准确探测出的个数比率，F1 Score为模型评价指标，它被定义为Precision和Recall的调和平均数。F1 Score的取值范围为0～1，F1 Score越大表示性能越好。结果表明，该实例中SSA-DBSCAN粗差探测法性能优异，探测效果最好；并且根据评价指标，本文提出的方法不仅能够准确识别粗差，而且在误判率方面优势明显。

表2 3种粗差探测方法的水平位移结果对比Table 2 Comparison of horizontal displacementobtained by three gross error detection methods

4.2 边坡钻孔地下水位监测序列

采用三板溪水电站东岭信边坡ZK2测点的钻孔地下水位监测序列为例(时间从2011年6月—2018年11月)，随机地在10、38、65、66、85、115、139、140、176、177期数处加入大小不一的共计10个粗差，形成复杂的含粗差监测数据，实测数据如图4所示。

图4 地下水位观测数据序列Fig.4 Original groundwater level data series

首先使用SSA法。选取窗口长度L为90。由于前6个重构分量的贡献率达到了99.9%，故选取前6个分量重构监测序列，其余分量组成残余分量。SSA结果如图5所示。

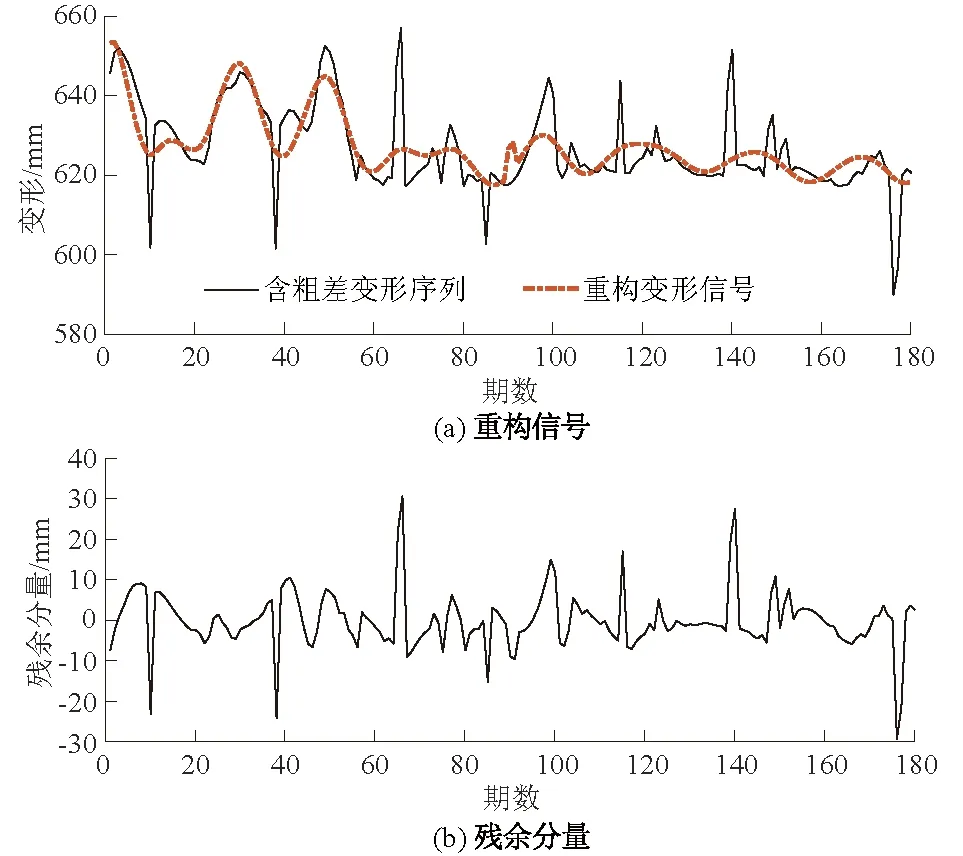
图5 地下水位序列SSA提取的重构信号及残余分量Fig.5 Reconstruction signals and residual componentsextracted from groundwater level data series by SSA

根据图5模极值点情况，然后定量计算残差序列的标准差获得阈值以进行可疑粗差点判别[5]，当残差绝对值>2σ(2σ=14.280 3 mm)时判定该点为可疑粗差点，可得10、38、65、66、85、99、115、139、140、176、177为可疑粗差点。

然后使用DBSCAN数据异常检测算法。通过对Eps和MinPts 2大参数联合调参，最终选取Eps和MinPts分别为5.5和3.0。DBSCAN数据异常检测结果如图6所示。根据试验结果：10、38、65、66、85、115、139、140、176、177点为噪声点，其余点为正常数据。接着，应用本文提出的SSA-DBSCAN粗差探测法，结果如表3所示。

图6 地下水位序列DBSCAN异常检测结果Fig.6 Result of DBSCAN anomaly detectionof groundwater level data series

表3 地下水位序列SSA-DBSCAN粗差探测结果Table 3 Result of gross error detection of groundwaterlevel data series based on SSA-DBSCAN

值得注意的是，地下水位与位移序列不同，强降雨往往会导致地下水位骤升，形成貌似粗差点的异常值，这些异常点是不能将其视为粗差去除的，故对于该类监测数据需要在本文提出的粗差探测算法基础上，联合降雨资料进行综合分析，具体如下：

(1)时序10、38、85、176、177若非粗差点，则意味着地下水位骤降，而实际上根据这些时序的降雨情况，如表4所示，不仅降雨量与近年同期相比变化不大，且与之对应的近年同期地下水位也并无骤降，表明上述时序并无骤降可能，均为粗差点。

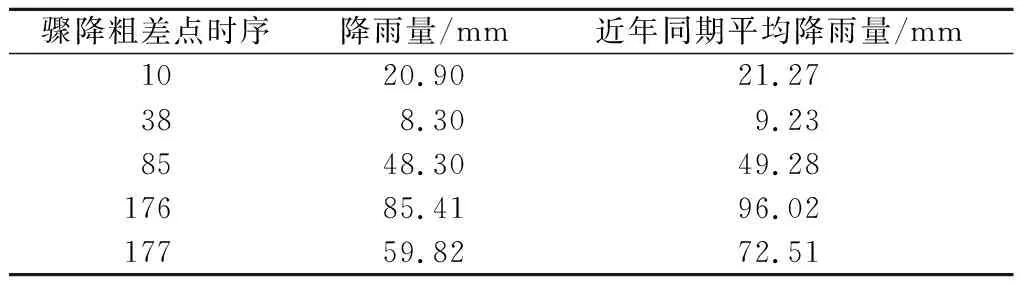
表4 结合降雨资料的骤降粗差结果分析Table 4 Analysis of abrupt drop of gross error resultin association with rainfall data

(2)时序65、66、115、139、140若非粗差点，则意味着地下水位骤升，而实际上根据这些时序的降雨情况，如表5所示，不仅大部分时序的降雨量远远小于同期最大降雨量，而且时序115、140的降雨量也都与往年(2015年、2017年)降雨情况相当，与之对应的同期地下水位也并无骤升。

表5 结合降雨资料的骤升粗差结果分析Table 5 Analysis of abrupt rise of gross error resultin association with rainfall data

一方面该滑坡已经修建了2条排水道，虽然突发的降雨短时间理论上会造成水位升高，但是在较长的15 d监测周期(时序)范围内，钻孔内突然汇聚的雨水有足够的时间消散。另一方面能威胁到该滑坡体稳定性的“久雨”被描述为在40 h内累计降下80 mm的雨水(对应日降雨量为50 mm/d)，而上述时序中15 d累计降雨总量的最大值也仅为47.31 mm。事实上，上述时序还均处于少雨的冬季。上述论述表明地下水位无骤升可能，即均为粗差点。至此，终于实现了对地下水位监测数据准确的粗差探测。

最后，为了验证该方法的优势，本文仍使用该钻孔地下水位监测序列，采用中位数绝对偏差法(MAD)和格拉布斯准则法(Grubbs)进行对比验证，如表6所示。结果表明，该实例中SSA-DBSCAN性能仍然优异，并且根据评价指标，本文提出的方法不仅能够准确识别粗差，而且在误判率方面同样具有显著优势。

表6 3种粗差探测方法的地下水位结果对比Table 6 Comparison of underground water level resultamong three gross error detection methods

5 结 论

考虑粗差存在的偶然随机性和监测数据的非平稳非线性特征，为解决边坡安全监测数据的粗差探测问题、并且进一步提升探测的精准性，本文提出了一种基于SSA和DBSCAN的粗差探测方法，并且以边坡水平位移和钻孔地下水位2组不同类别的安全监测数据为例进行了实证研究，得到以下结论：

(1)本文提出的SSA-DBSCAN粗差探测法面对2组不同类别的边坡监测数据，依赖性能突出的DBSCAN异常检测算法均能准确探测出全部的粗差。并且该方法在与MAD和Grubbs准则法的对比验证中体现出了更高的精准性，尤其在误判率方面优势明显，上述2组不同类别监测序列的实证分析更表明该方法具有一定的普适性。

(2)本文提出的SSA-DBSCAN粗差探测法更适用于对变形监测序列的粗差探测，如大坝、边坡变形引起的监测点位移变化。但是监测数据如地下水位、温度等复杂多样，这类监测数据与变形数据不同，其出现的突变离群值并不一定是粗差，如果盲目地剔除，则错过了反映真实情况的重要数据，因此，实际中我们需要联合其他监测资料对其进行综合研判。

(3)本文提出的SSA-DBSCAN粗差探测法虽然结合降雨资料综合分析能够实现对地下水位这类相对复杂监测序列的粗差探测，但这是建立在专业技术人员的时间人力成本上的，而实际中难以满足这样的条件，故本文提出的方法虽然在变形监测序列中具有一定的推广前景，但在应对地下水位这类监测数据上存在一定的局限性，还需进一步研究探索。并且近年来人工智能、深度学习理论正在如火如荼地发展，如何结合这些理论构建智能粗差探测识别系统是未来发展的方向。