基于ＣＦＤ的顺直明渠断面流场数值模拟研究

程科　罗强　宁芊等

关键词：顺直明渠;刚盖假定法;VOF法;湍流模型;CFD;流速分布

中图分类号：TV62 文献标志码：A doi：10.3969/j.issn.1000-1379.2022.03.031

引用格式：程科，罗强，宁芊，等.基于CFD的顺直明渠断面流场数值模拟研究[J].人民黄河，2022，44（3）：160-164.

明渠水流是自然界和水利工程中常见的流动形态，了解明渠水流的流速分布对于研究其水沙运动规律、河流修复以及水资源调度具有重要意义[1]。常用流速测量技术如多点流速仪测量技术、利用多普勒效应的激光技术、通过热传递引发电压变化的热丝和热膜技术在应用过程中测得数据量十分有限[2]，无法满足精度要求。数值模拟采用离散方法对流体运动控制方程进行求解，可以避开以上测量技术并得到大量数值计算结果，因此采用数值模拟方法研究明渠断面的流速分布是一种有效途径。考虑到计算机内存资源的消耗，实际工程中的数值模拟通常基于求解RANS方程来实现，需要选择合适的湍流模型封闭方程。Launder等[3]提出的标准k-ε模型假定流场为各向同性的完全湍流，流体分子之间的黏性可以被忽略，因此该模型只适合完全湍流的流场模拟，对非均匀湍流等复杂流动的模拟性能较差，为弥补其不足，Yakhot等[4]基于重组化群数学方法提出了RNGk-ε模型，该模型考虑了湍流流动中的旋转及旋流，可以更好地处理高应变率及流线弯曲程度较大的流动。相比上述2种模型，RSM模型考虑了湍流的各向异性效应，在计算湍流输运各向异性较强的流动时表现较优。由于实际工程中明渠水流的自由水面是随时间和空间不断变化的，因此在数值模拟过程中自由水面的处理尤为重要。目前自由水面处理方法主要有MAC法、质点网格法、刚盖假定法、VOF法等[5]，其中：刚盖假定法直接假定自由水面为刚性平面，适用于水面波动不大的情况;VOF法通过建立欧拉网格并定义体积函数来追踪自由水面，计算量小且精度高，能有效处理自由水面折叠的强间断问题[6]。

目前大多数灌区明渠为梯形明渠，为准确评价顺直明渠断面的流速分布，笔者选取梯形明渠流场为研究对象，依据CFD方法并借助Fluent软件建立了三维顺直明渠流场数值仿真模型，通过对比渠道断面中垂线上的模拟流速与实测流速来证明所建立数值模型的有效性。

1顺直明渠湍流模型

将研究对象假设为三维、稳定、不可压缩的连续流体。质量守恒方程和动量守恒方程分别为

2明渠断面流场数值模拟

对于明渠断面流场的数值模拟，考虑空气域的作用，水域高度和空气域高度比值应不小于1/3[7]。为避免明渠断面流速分布受到上游入口和下游出口的干扰，需要对计算模型的渠道长度进行确定以使流场充分发展。通过设置不同区间的渠道长度并分析断面流速分布情况，得出上游入口距下游出口为20～30倍渠道底宽时，各断面流速分布较一致，不受上下游未知边界效应的影响。笔者将计算模型的渠道长度设置为30W（W为渠道底宽），计算区域的坐标原点O位于上游入口明渠床面，计算区域示意见图1。

2.1自由水面处理

采用刚盖假定法和VOF法分别对自由水面进行处理。刚盖假定法是将自由水面假定为一个规则的刚性平面，各变量在自由水面的法向分量均为0，水面位置不随时间变化而变化，此时自由水面转变为边界条件，类似于可滑移壁面条件;VOF法是通过建立固定的欧拉网格，记录单元网格中流体体积与网格体积的比值（函数F）来构造和追踪自由水面[8]。

2.2数值方法和边界条件

采用有限体积法离散控制方程，采用PISO算法对压力-速度场进行解耦[9-10]，除压力计算采用体积力加权方法外，其余变量均采用二阶迎风格式离散。采用刚盖假定法时，计算区域仅为水域;采用VOF法时，计算区域分为水域和空气域，对六面体结构化网格进行剖分，在边壁处和自由水面处进行网格加密。对于边界条件，采用刚盖假定法时，上游进水口为流速进口，下游出水口为自由出流，使用对称边界条件定义外部自由边界;采用VOF法时，上游进水口为流速进口，上游空气入口为质流进口，下游出水口和空气出口均采用压力出口，使用压力进口边界条件定义外部自由边界。

3结果分析

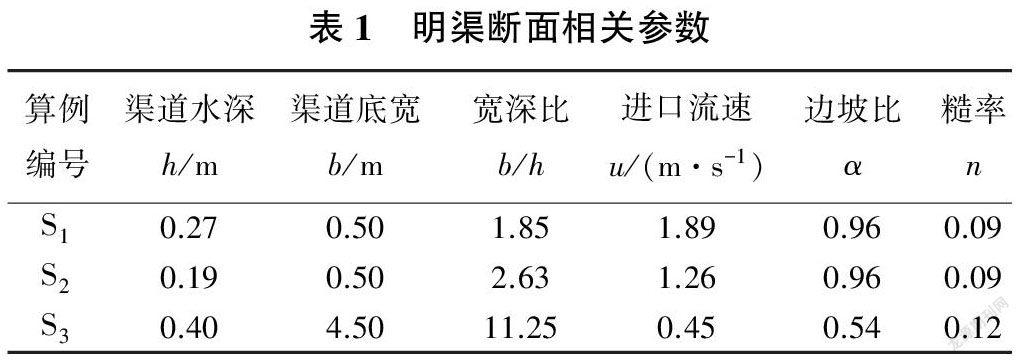
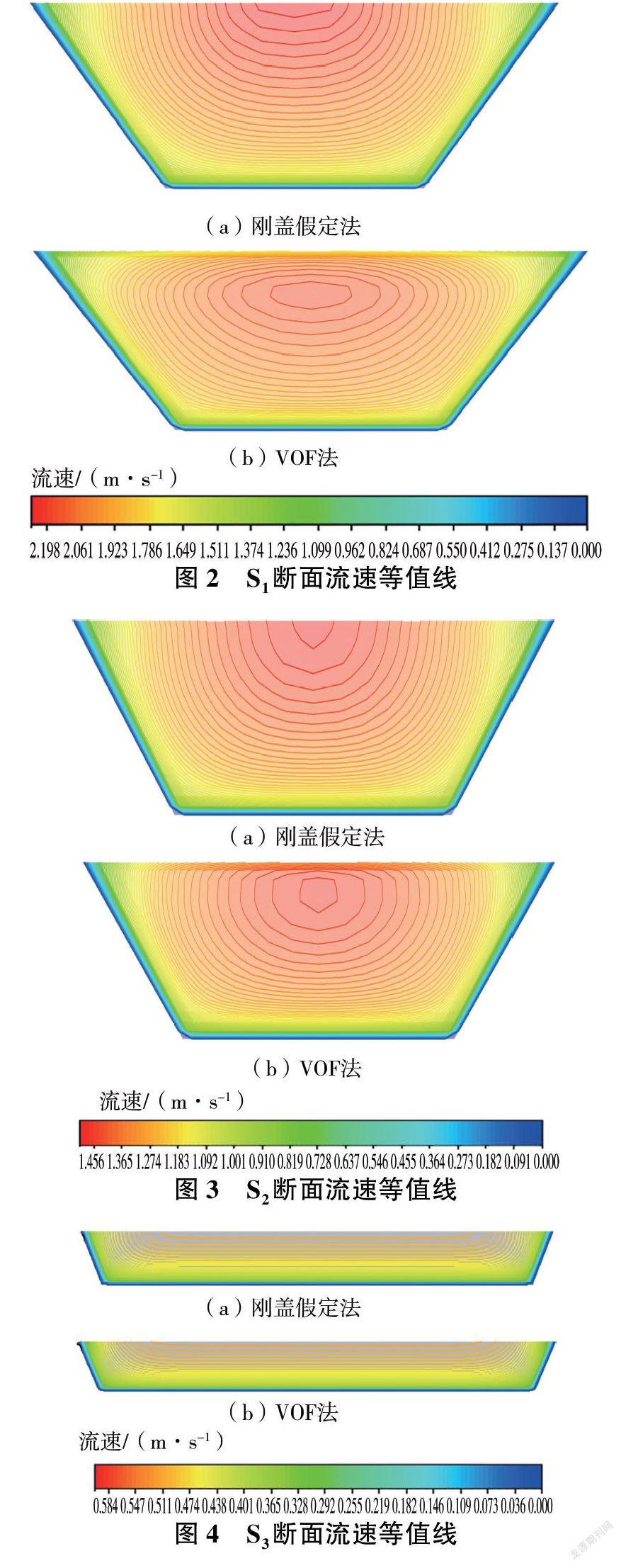
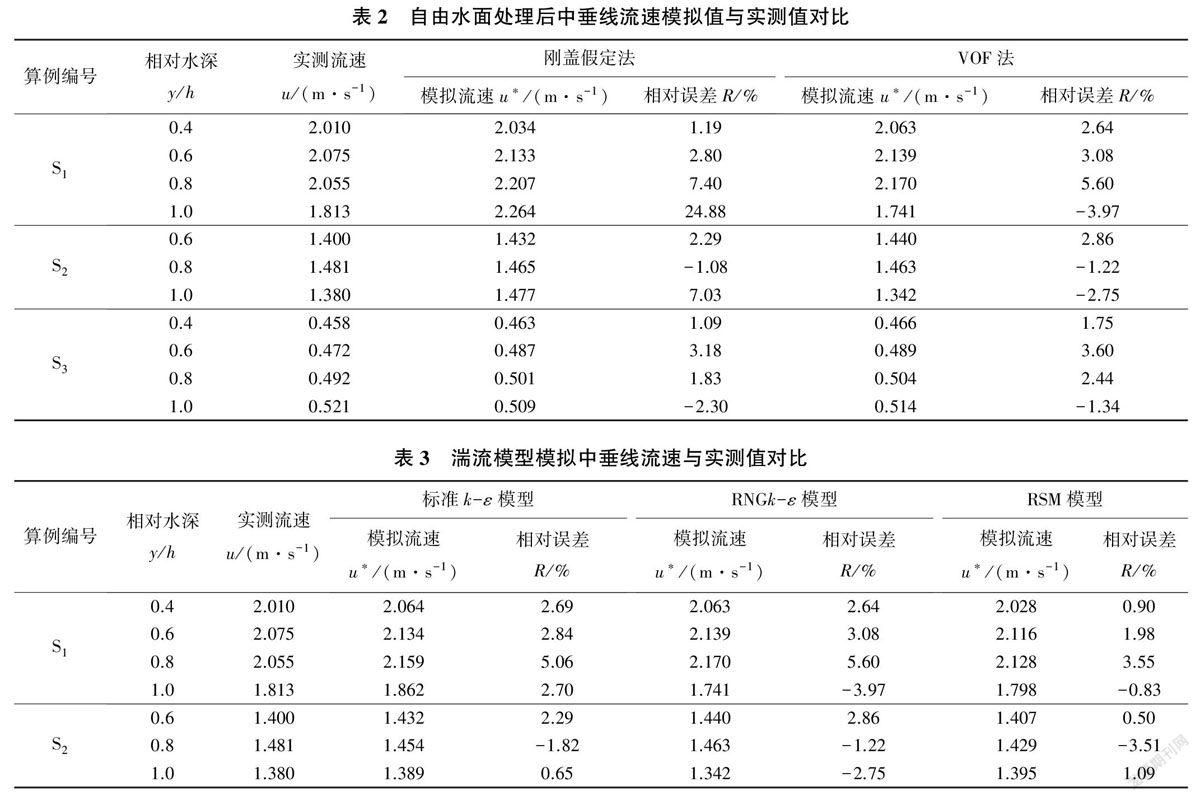
当明渠平均宽度与深度比值小于5时，将其定义为狭窄明渠，相反则为宽浅明渠[2]。选取了3组不同宽深比的梯形明渠分别对其流场分布进行数值模拟研究，其中算例S1和S2对应狭窄明渠，算例S3对应宽浅明渠，实验数据来自某灌区渠道实测数据，渠道相关参数见表1。

3.1断面流速等值线模拟结果

Mahananda等[11]的研究结果表明在狭窄明渠中，二次流的影响会导致流速最大值出现在自由水面之下的倾角现象。采用刚盖假定法和VOF法分别处理明渠自由水面，不同宽深比明渠的断面流速等值线模拟结果如图2～图4所示。可以看出，对于算例S1明渠和S2明渠，采用刚盖假定法时，断面流速最大值均出现在自由水面之上，无法模拟出倾角现象;采用VOF法时，断面流速最大值位于水面之下，可以模拟出倾角现象。对于算例S3明渠，采用刚盖假定法和VOF法时，断面流速最大值均位于水面，且两种等值线模拟结果基本相同。以上结果表明VOF法更加适合模拟有倾角现象的狭窄明渠，刚盖假定法更加适合模拟宽浅明渠。

3.2中垂线流速分布对比

为验证数值模型的有效性，以RNGk-ε模型为例，对不同自由水面处理方法得到的渠道断面中垂线上的模拟流速与实测流速进行对比，见表2。采用VOF法时，3个算例明渠的模拟流速与实测流速相对误差均在6.00%以内。采用刚盖假定法时，当相对水深小于0.6时，模拟流速和实测流速吻合较好，而相对水深较大时，由于刚盖假定法无法模拟宽深比较小的狭窄明渠，因此算例S1明渠和S2明渠的模拟流速与实测流速偏差较大;对于算例S3明渠，刚盖假定法误差略小于VOF法。这一对比结果再次证实了在有二次流的狭窄明渠中应采用VOF法处理自由水面，在无二次流的宽浅明渠中应采用刚盖假定法处理自由水面。

3.3湍流模型对比

在狭窄明渠中，流速分布受二次流影响会出现倾角现象，且明渠宽深比越小，此现象越明显，其湍流情况比宽浅明渠更加复杂，因此有必要对宽深比较小的狭窄明渠进行湍流模型优劣的评估。

选取标准k-ε模型、RNG k-ε模型、RSM模型分别对算例S1和S2明渠进行数值模拟，同样对渠道断面中垂线上不同相对水深的模拟流速和实测流速进行对比，见表3。可以看出，对于宽深比最小的算例S1明渠，RSM模型的模拟结果最佳，而对于宽深比相对较大的算例S2明渠，RSM模型的模擬结果相比标准k-ε模型和RNG k-ε模型较差。

由于顺直明渠中的雷诺压力为各向同性，而RSM模型更适用于雷诺压力为各向异性的湍流情况，且该模型在宽深比稍大的明渠中模拟精度降低，因此RSM模型不适用于顺直明渠模拟。标准k-ε模型和RNGk-ε模型的模拟结果相差不大，笔者又对其他明渠进行了仿值模拟研究，限于篇幅没有列出，结果均显示RNGk-ε模型收敛速度更快且模拟误差更加稳定，因此对于顺直明渠模拟，最佳的湍流模型为RNGk-ε模型。

4结论

笔者依据CFD方法建立了顺直梯形明渠的数值仿真模型，利用3种湍流模型封闭RANS方程，通过刚盖假定法和VOF法捕捉自由水面，并采取PISO算法对压力-速度场进行了解耦。模拟结果和实测结果对比表明：VOF法适用于狭窄明渠，能够模拟由二次流导致的倾角现象;刚盖假定法更加适用于宽浅明渠。湍流模型模拟结果表明，RNGk-ε模型的模拟误差更稳定，更加适用于顺直明渠断面流场的数值模拟。通过对比渠道断面中垂线上的模拟流速与实测流速，证明了所建立数值模型的准确性，可为其他复杂的明渠流场模拟提供参考，以更加高效快速地建立适用的明渠数值模型。

【责任编辑 栗铭】