Volta's混沌系统同步控制
2022-04-15王东晓李自强
王东晓,李自强
(郑州航空工业管理学院 数学学院,郑州 450046)
0 引言
混沌现象是指发生在确定性系统中的不规则运动,一个确定性理论描述的系统,其行为却表现为不确定性一不可重复、不可预测,这就是混沌现象。混沌是非线性动力系统的固有特性,是非线性系统普遍存在的现象。牛顿确定性理论能够充分处理的多为线性系统,而线性系统大多是由非线性系统简化来的,在现实生活和实际工程技术问题中,非线性系统普遍存在,混沌是无处不在的。混沌理论所研究的是非线性动力学混沌,目的是要揭示貌似随机的现象背后可能隐藏的简单规律,以求发现一大类复杂问题普遍遵循的共同规律。
随着研究的深入,混沌系统的广泛存在,混沌同步一直是非线性科学研究的热点。混沌系统的同步有着广泛的应用前景,同步问题备受关注,新的系统新的方法层出不穷。毛北行等[1]研究了非线性复杂网络混沌系统的有限时间同步问题;较早出现的自适应方法也常常用于整数阶或分数阶混沌系统同步[2-3];张燕兰采用自适应方法实现分数阶Rayleigh-Duffling-like系统的广义投影同步[4];近年滑模同步方法常被用以混沌同步[5-6],余明哲等[7]表明滑模自适应同步了一类不确定分数阶系统;钟启龙[8]等采用主动滑模研究了分数阶混沌系统同步问题;也可用类似的方法研究整数阶、分数阶同步问题[9];两个不同系统的同步也可以利用自适应滑模控制来实现[10]; Volta's混沌系统[11-12]在物理、通讯等方面有着广泛的应用,张振等[13]研究了分数阶Volta's系统同步问题;李娇研究了Volta's系统的混合投影同步[14];张志明等[15]对Volta's混沌系统添加一个新的状态变量,得到一个四维的自治超混沌系统。在上述研究的基础上,本文研究了三维和四维Volta's混沌系统同步问题,给出了系统取得同步的充分性条件,最后的数值仿真结果表明该方案的有效性和可行性。
1 主要结果

此时系统呈现混沌态,如图1。在系统(1)中添加一个新的变量,并令=x+r,当r∈[-40,-32]∪[32,40],得到一个四维超混沌系统[15]:

图1 三阶Volta's系统的混沌吸引子
考虑如下三阶Volta's混沌系统[11-12]:

取值 20,混沌吸引子如图2。

图2 四阶Volta's系统的混沌吸引子
以系统(1)作为驱动系统,其对应的响应系统设计为:
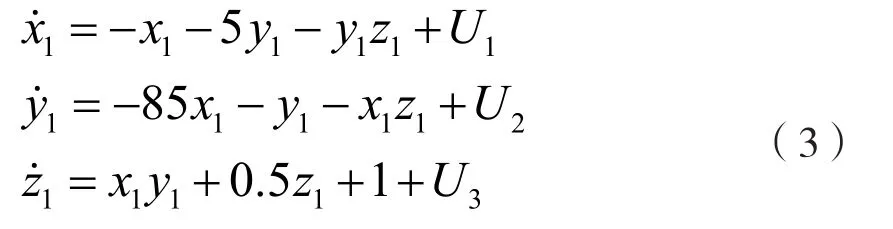
其中ui,(i=1,2,3)为控制器,令误差变量ei=yi-xi,(i=1,2,34),从而误差系统如下:

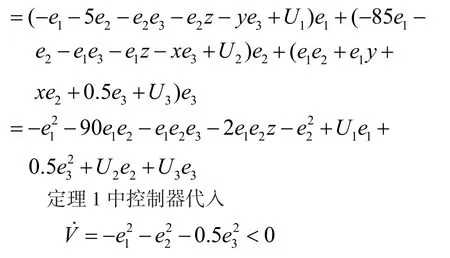
系统(1)与(3)同步。
在定理1中,构造的控制器含有非线性项,我们尝试线性控制器来实现混沌系统同步。系统(1)呈混沌态,系统变量有界,存在常数Q,M,N > 0,满足。得到如下定理。

下面考虑四维Volta's混沌系统的同步控题。考虑如下的响应系统:
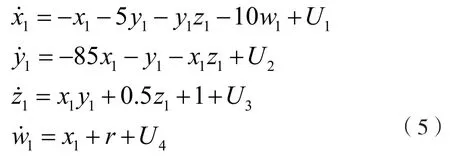
误差系统如下:
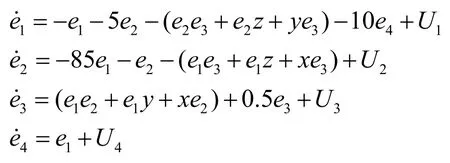
定理3:系统(5)在如下控制器作用下:

主从系统(2)与(5)是同步。
证 明:选择Lyapunov函数,则Lyapunov函数关于时间的导数为:

系统(2)与(5)同步。
从上述推导过程当中可以看出,该控制方法非常灵活,控制器的第二部分可以任意构造,只要满足矩阵A为负定矩阵,满足李雅普诺夫稳定性理论的条件,就可以保证误差系统在零点渐进稳定。当然,所构造控制器越简单,实现同步所用时间越短,控制方案也就越好。
2 数值仿真
以matlab为工具,对各种方案分别做出数值仿真。系统(1)状态变量初始值(8,2,1),系统(3)状态变量初始值(1,4,8)。图3为在定理1所设计方案控制下的误差系统曲线,图4为在定理2所设计控制方案控制下的误差系统曲线,从误差曲线可以看出,两种方案都可以很好地实现系统同步,定理2方案中的控制器为线性控制器,相较于定理1的方案更加简单,在实际操作中更加容易操作,在加入控制器后主从系统状态很快趋近一致,实现同步;且实现同步的时间更短,更具有优势,并且在做仿真的过程当中,控制器不满足定理条件时,也有可能实现同步,原因是我们给出的条件仅仅是充分条件,而非必要条件。系统(2)状态变量初始值(8,2,1,1),系统(5)状态变量初始值(1,1,2,8),图5 为在定理3设计方案控制下系统误差曲线,图6为系统(2)和系统(5)的状态变量曲线。
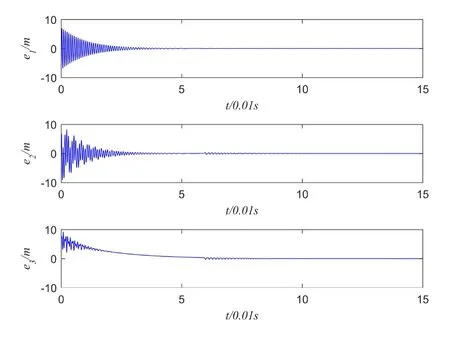
图3 定理1的系统误差曲线
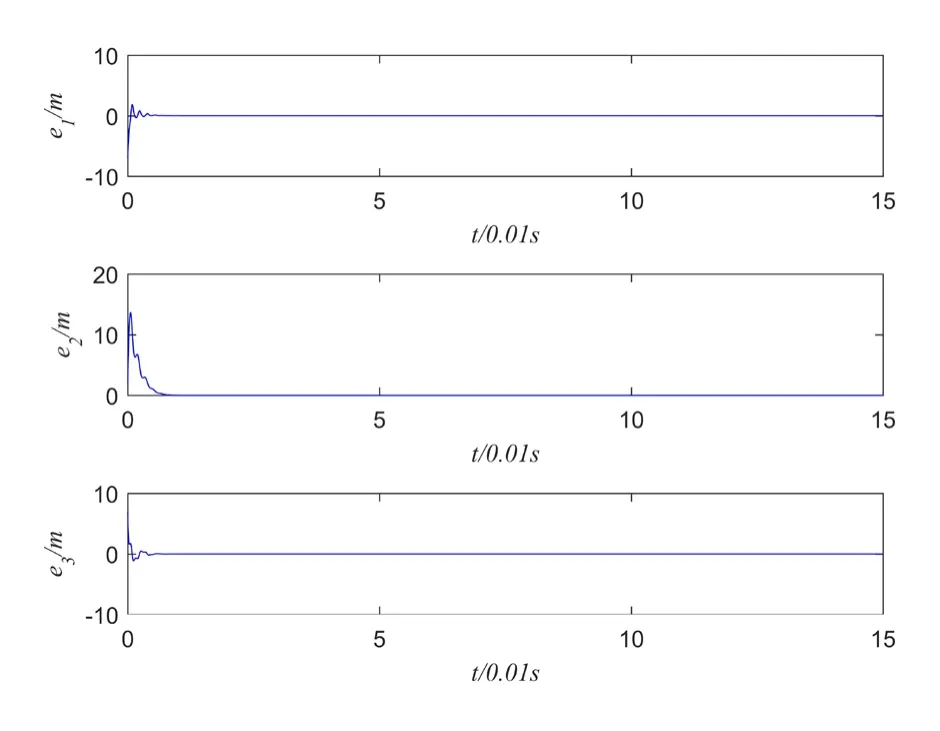
图4 定理2的系统误差曲线

图5 定理3的系统误差曲线

图6 定理3的主从系统状态
3 结论
本文主要研究了Volta's混沌系统的同步控制问题,分别对三维和四维混沌系统设计了控制方案,得到了整数阶Volta’s混沌系统同步的充分性条件,给出了严格的数学证明和推理过程,数值仿真表明该方法有效性和可行性。
