基于MATLAB的复合因子方差分析与主成分分析算法设计

薛亚宏，王 嘉，程喜林

（1.甘肃工业职业技术学院 经管学院，甘肃 天水 7410252；2.兰州大学 信息科学与工程学院，兰州 7300003；3.西北大学 城市与环境学院，西安 741069）

方差分析（Analysis of variance，ANOVA）是英国统计学家兼遗传学家Gitbert提出的一种分析方法，在林业遗传、科学试验、医学研究等众多领域有极其广泛的应用[1]。方差是统计量分析中的一类，是假设检验与区间估计的推广和延伸，由于试验样本的成因方式不同，一般采用的分法方法也有所差异，在统计学界，通常用单因子（one-way）、复因子（double-way）或多因子（N-way）方法。

主成分分析是根据已有数据推断假设数据受某主要因素影响程度的一种分析方法，其本质仍为假设检验[2]。通常需要提供理论样本结果和实测样本结果，两者通过矩阵排列得到回归模型，最终得到影响总体数据分布的主要因素及数值，一般要采用二维或三维曲线进行二次以上模拟，在误差允许范围内满足达到精度即终止计算。

1 复合因子方差分析

复因子分析即有两个影响因子。通常应用于医学疗效的验证，其一般的分析步骤为：首先将病人随机（一般、等距、整群）分为k组，每组有x人，将每位病人的疗效监测指标记为tm,n，其中下标m、n分别表示第m组，（i=1,2,…,k），n表示某组内病人的诊疗编号，（n=1,2,…,w），则第m组的第n个病人的监测指标即为tm,n。按照MATLAB特有的表达式记号，记第k组所有病人的所有监测指标为tm，或各组的第w位病人的监测标为tn，则这样计算出向量，这涉及算术平均数的范筹，如此则构造出标准方差分析表，并根据所给出的监测数据找出效果分析数据。

以上所采用药物作为分组的依据，称为复因子（Complex factor），它们的差异均值称为复水平。其中m值与p值较为关键，直接影响概率值p＜a的置信度及拒绝假设目标H0，否则假设不成立，疗效分析验证为假。

在MATLAB中，anoval0、anova2可分别进行单因子、复因子分析，并有效地给出较为精确的结果，其基本格式为[p,Tab,Stats]=anova1(Q)[3]，其中，Q为需要分析的数据，该数据是一个k×w矩阵，其行对应于分组号，运算结果会返回检验值s，以及检测数据表Tab；该函数还将打开两个主程序窗口viewer和power，分别以表式、盒式结构呈现。

1.1 单因子分析（疗效分析方向）

案例1：以非吗啡类中枢型镇痛药物盐酸曲马多（Tramadol）为例[4]，现将40个病人（医学低于30为小样本）样本分为6组，每组5人，患者（patient）使用同一药物（假定无其他辅助药物），记录从用药到痊愈时间（h），观测所用药物的疗效是否存在显著差异，观测数据如表1所示。

表1 痊愈时间观测数据表

算法设计：

基于以上监测数据，现构造出一个5×6型矩阵，命名为矩阵Q，对各组数据采用复因子方差分析，得出以下分析结果：

在程序运行过程中，anoval（）会自动呈现两个窗口，分别是盒式图、分析表，同时显示概率值p，其中a=0.03或0.04，表示置信水平，显然从结果来看应拒绝假设，即药物对痊愈时间有显著影响。

1.2 双因子分析（植物培育方向）

案例2：以岩松、油松、赤松3种松树树种在甘肃省天水市小陇山林区党川、利桥、草川、草滩4地（林场）的生长情况为例，每地每类树种选择6株，测量其胸径，并进行双因子方差分析，观测数据如表2所示：

表2 甘肃省小陇山林区岩松等3类松树生长观测数据

Q算法设计：

基于以上监测数据，现调用anoval2（）函数，命名为矩阵H，对各组数据采用双因子方差分析，anoval2（）命令及矩阵列排列如下：

从结果来看，由于PA=0.01393，所以应该拒绝H1假设。可以初步推断，列数据对监测结果有显著影响，即小陇山林区下辖党川等4地3类松树树种对其胸径有显著影响。

以下计算均值，以反映不同树种在同一林场生长差异：

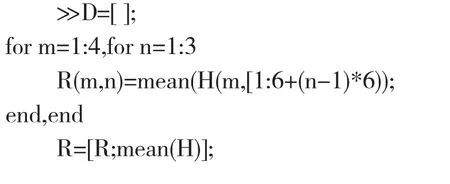
根据结果分析，赤松胸径明显大于岩松和油松。PH与PHQ的差距较大，从而判断假设为真，故接受假设[5]。即党川等4地各自对3类松树树种的胸径有轻微影响，不同区域（林场）对不同松树树种胸径成长无显著影响。

2 主成分分析

主成分分析是一种常见的多因素分析方法，在信息模拟、疾病预防、地理信息采集、工程造价测算、农作物产量分析等领域有着广泛应用[6]。通常采用SPSS、R等平台进行分析，但由于原数据类型的多样性，输出图形特征的两极分化（异端非同步）现象较为普遍，经与实际监测比对出现较大偏差，结论不稳定，因此不具有代表性。在这种情况下，利用MATLAB在数据降维处理方面的精度、效度以及在图象表现上的多维仿真优势，通过调用Corr（）函数，建立协方差矩阵及特征向量、主成分贡献率及累计贡献率、建立变量指标方程组对数据进行降维处理，实现源数据分析从多维到低维的转化。

2.1 基于MATLAB的主成分分析算法原理

首先建立协方差矩阵

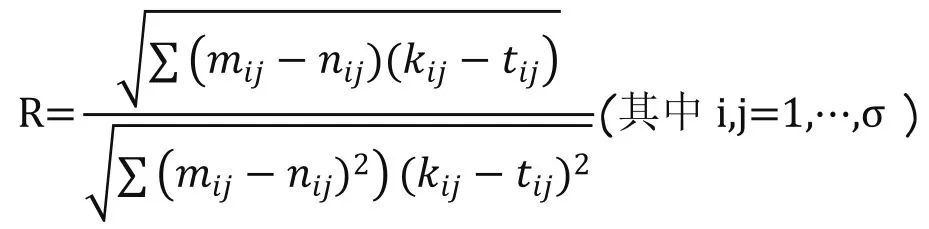
再根据R计算出特征向量ei及特征值，做反序处理；

最后，通过转换变量（降维），构建平面坐标方程zi=azi+bzi+Ri，获取主体变量影响因素间的关系构成，即主成分分析的基本表达式。

2.2 三元主成分分析（高程测量方向）

案例3：以甘肃省天水市李子园铅锌矿第四纪浅层地貌特征分析为例，某测量点三维坐标参数分别为 x=ωcos2ω, y=ωsin2ω, z=0.887x+3.463y，现通过MATLAB生成一维数组，并输出以2个测量数位为基本单位矢量模拟表达式。

算法设计如下：

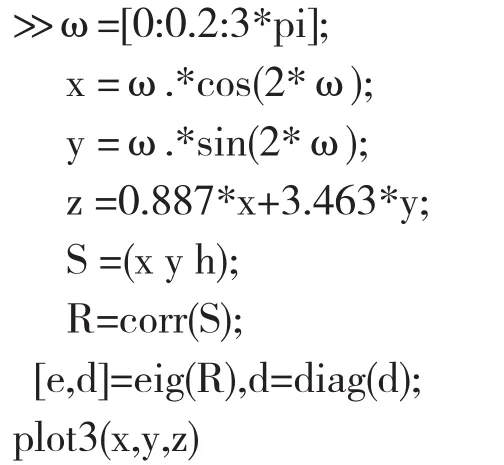
显然，基于对降维矢量输出原理的分析，进一步利用空间坐标变换，对三维原数据做放样投影，得到二维数组[7]。

执行以上命令，输出结果为：

值得注意的是，结果中的σ向量、e向量非测量高程测序排列，要通过fliplr（）函数和real（）函数执行反序和翻转输出，目地是使特征值按常规测序呈现，为RNSS测绘系统数据导入做必要的前期配置。

具体语句如下：

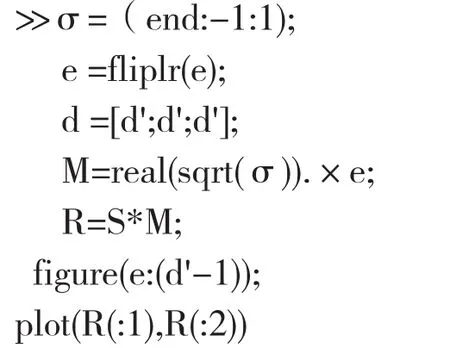
转换后的3×3矩阵提供二维数据（z列为0）如下：

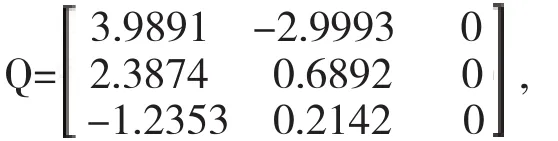
故新坐标系可表示为：

该坐标方程实现了对三维高程测量数组的降维（纵向投影），通过坐标转化使RNSS源数据压缩于二维平面上，一方面能准确表现该区域第四纪地貌分布特征，另一方面在同类型矿区主要作业区域地形图绘制（表层、浅层）中提供了满足绘制精度要求的一种新的计算途径，其误差范围与多基点均匀采样在同一水平[8]，但其在数据生成原理、仿真形式以及中间变量转换等多个方面集成了ArcGIS、C++的优势，有效降低了测图成本。

3 结语

基于MATLAB的复合因子方差分析与主成分分析计算原理清晰，算法逻辑性强，语法调用灵活。在实践中，以应用统计学基本计算理论为基础，结合矩阵运算、坐标变换等数学手段，最终通过MATLAB实现对样本数据的终端处理，有效弥补了SPSS、R等分析工具在图像拟合优度与坐标维度无法兼顾的不足，特别是三维数字测图、工程概预算、造价分析等领域内能大大地降低数据交叉，有效降低项目成本，有较强的实用意义。