小学生视觉空间推理能力内涵及其表现测评
2022-04-15刘晓莉孙兴华
刘晓莉,孙兴华
(东北师范大学 教育学部,吉林 长春 130024)
视觉空间推理是一种创造和操作视觉图像的过程,对儿童几何思维的发展起着不可替代的作用,它不仅是人类智能结构的重要组成部分,也是数学核心素养的重要组成部分,是学生必须掌握的关键数学能力。要想进一步促进小学生几何思维的发展,就需要发展他们的视觉空间推理,把推理、视觉表象及可视化思维植入进小学生数学思考过程中。随着义务教育阶段数学课程改革的不断深入及新一轮小学课程标准的修订,将空间观念、几何直观和推理能力作为义务教育阶段的数学核心素养,相关学习内容无疑会成为关注的焦点。虽然新课程中并未明确提出视觉空间推理,但其作为空间观念的发展,是世界各国数学课程改革的新动向,也是我国小学数学课程改革应关注的热点话题。因此,需要增进小学数学教师对视觉空间推理的关注,这对促进学生空间想象能力和创新能力的发展都有着重要意义。
目前国外有较多的实证研究对其进行了探讨,并取得了一定的研究成果,但是,由于研究视角不同,对视觉空间推理的内涵还没有形成统一的认识。目前,我国从心理学视角进行的探讨多一些,从数学教育视角的研究还不够丰富。基于此,本研究尝试在梳理相关概念的基础上,探讨小学生视觉空间推理能力的内涵,尝试建构小学生视觉空间推理能力表现的测评框架,以小学高年级学生为研究对象,编制测评工具并开展测评实践,以期为小学数学教师如何评价学生视觉空间推理能力的表现,以及如何发展小学生的视觉空间推理能力提供参考。
一、 视觉空间推理概念的意蕴
视觉空间推理由“视觉空间”和“推理”两个词组成,视觉空间(即空间)是物质存在的客观形式,即由长、宽、高所构成的三维空间;推理不仅仅是人们日常生活和学习中经常使用的思维方式,也是数学的基本思维方式之一(1)中华人民共和国教育部:《义务教育数学课程标准(2011年版)》,北京师范大学出版社2012年版,第6页。。作为把空间观念和几何推理有机结合的一种几何思维和能力形式,视觉空间推理的相关概念涉及心理学和数学两个方面。
如表1所示,从心理学的视角来看,与视觉空间推理有密切联系的概念有:空间知觉(spatial sense)、空间表象(spatial imaginary)、空间想象(spatial visualization)和空间能力(spatial ability)。其中,空间知觉以空间表象为基础,空间想象是空间表象的发展,而空间能力是一个总的概念,涵盖上述几种能力,它不同于一般的形象思维和抽象思维能力(2)刘晓玫:《小学生空间观念的发展规律及特点研究》,东北师范大学2007年硕士学位论文。,主要是特定领域内的思维能力。

表1 视觉空间推理相关概念梳理
从数学的视角来看,与视觉空间推理有密切联系的概念有:空间观念、几何思维、几何直观和几何推理。其中,空间观念以空间表象为主要表征形态,还包括一定的命题表征,并涉及空间知觉和初步的空间想象。所以当提到“空间观念”一词时,不可避免地会将其与空间想象联系起来。然而在小学阶段,空间想象对学生认知发展的要求较高,尽管如此,培养小学生的空间想象能力是完全有可能的,只是对于大多数小学生来说,空间观念更有普遍意义(3)史宁中:《通过度量,巧用技术,发展空间观念——评析“让画出的图形转起来”一课》,《小学数学教师》2019年第9期,第42-43页。,因而只需要发展作为空间想象基础的空间观念即可(4)孔凡哲,曾峥:《数学学习心理学》,北京大学出版社2009年版,第199页。。此外,在培养空间观念的过程中,还需要同时关注几何直观和几何推理(5)史宁中:《人是如何认识和表达空间的》,《小学教学(数学版)》2019年第3期,第13-16页。。空间观念和几何直观是互为基础的,直观感知是建立空间观念的基础,而直观洞察是空间观念的发展与升华。然而二者也各有侧重,空间观念倾向于即使脱离了背景也能想象出图形的形状、大小及其关系的能力;几何直观更强调借助一定的直观背景条件而进行整体把握的能力(6)孔凡哲,史宁中:《关于几何直观的含义与表现形式——对〈义务教育数学课程标准(2011年版)〉的一点认识》,《课程·教材·教法》2012年第7期,第92-97页。。同时,几何直观与几何推理也有着密切的关系:一方面,几何推理需要借助几何直观来发现几何规律;另一方面,几何推理可以验证几何直观的发现。如果把几何推理视为演绎推理,几何直观则可以视为合情推理。
以上关于视觉空间推理的诸多概念间存在着紧密的关系,是视觉空间推理内涵下不同层次水平的再现。空间观念和空间想象是视觉空间推理的重要组成,空间观念是发展的基础,空间想象则是空间观念的发展和提升。此外,空间想象是几何思维的重要方面,是空间能力的主要因素之一,而空间能力又是视觉空间推理的一部分。但相较于空间观念或空间能力来说,视觉空间推理有着更加广泛的含义,它不仅指能力,也是一种活动化的思维过程,即是一种关于对物体的视觉空间信息得出结论的心理活动(7)Kho R. Penjenjangan Penalaran Visuospasial Siswa dalam Menyelesaikan Masalah Geometri.SEMINAR NASIONAL. 2016, 1(1).。
二、 小学生视觉空间推理能力的内涵
在视觉空间推理过程中,主要包含两种核心成分:一是可视化思维,即内部(心理)表征或外部表征,这是最一般的能力因素,主要体现在旋转、反射、组合图形、多重变换图形、复杂图形的折叠等活动中。二是视觉表象,表象是客观事物在个体头脑里留下的概括形象,而视觉表象主要用于在头脑中储存信息,并创造和操作视觉图像,是视觉空间推理的重要基础。这种可视化和视觉表象可以帮助人们将问题的相关要素联系起来以促进问题解决,在建立几何知识的概念理解和空间理解方面都具有重要的作用(8)Steenpaβ A, Steinbring H. Young Students’ Subjective Interpretations of Mathematical Diagrams: Elements of the Theoretical Construct Frame-based Interpreting Competence. ZDM, 2014, 46(1),pp.3-14.。
目前,更多的研究是从心理学或数学方向出发来考察学生几何思维的发展水平。人们最熟知的是皮亚杰的研究,皮亚杰等人(Piaget et al.)关于儿童空间概念的理论主要包括两个观点:第一,空间感是通过儿童主动或内化行为逐渐组织而构建起来的,进而形成运算系统。因此,儿童的空间感是从以前的操作活动中积累起来的,需要同化和顺应的过程,而不是直观识别空间环境。第二,儿童在几何方面的发展顺序同历史上所发现几何的顺序正好相反,经历了拓扑关系(3—6岁)、射影几何(6—8岁)以及欧式几何(9岁以后)三个阶段(9)Piaget J , Inhelder B , Szeminska A , et al. The Child’s Conception of Geometry. Basic Books, 1960.。范希尔夫妇(Pierre Van Hiele & Dina Van Hiele)基于皮亚杰的数学理解水平,结合几何教学过程中所遇到的问题,提出几何思维的五个水平,包括视觉(visualization)、分析(analysis)、非形式化演绎(informal deduction)、形式化演绎(formal deduction)、严密性(rigor),这五个水平有着一定的顺序,学生在进入某一水平学习之前,必须掌握之前水平的大部分内容(10)Van Hiele P M. Structure and Insight: A Theory of Mathematics Education. 1986.。对小学生来说,他们的几何思维主要处于前三个水平。
在此基础上,很多学者又进行了大量相关的研究。本研究关注了与视觉空间推理能力关联较多的研究,比如皮塔利斯和克里斯托(Pittalis & Christou)提出学生的几何思维应包括表征三维物体、空间结构、测量和概念化数学属性四种类型,而空间能力包括空间可视化、空间定位和空间关系三种因素(11)Pittalis M, Christou C. Types of Reasoning in 3D Geometry Thinking and Their Relation with Spatial Ability. Educational Studies in Mathematics. 2010, 75(2),pp.191-212.。同时,他们还建立了一个模型来描述学生表征三维图形的能力,包括识别和构建视图、从二维向三维转换、构建三维图形的平面表示、解释三维图形的结构要素以及解释三维图形的几何属性五种(12)Pittalis M, Christou C. Coding and Decoding Representations of 3D Shapes. The Journal of Mathematical Behavior. 2013, 32(3),pp.673-689.。另外,在数学教育研究中,我国有的学者从空间观念的内涵出发,将空间观念的表现形式分为形状识别、运动变换、方位距离、几何度量、图形绘制五个维度(13)宋乃庆,王诗梦,罗士琰:《小学生空间观念:内涵、价值及表现形式》,《教育与教学研究》2021年第6期,第44-54页。;还有研究者根据课标中有关空间观念具体表现的阐述将其确定为四个维度:轴对称、旋转、视图和方向与位置(14)刘晓玫:《小学生空间观念的发展规律及特点研究》,东北师范大学2007年硕士学位论文。;也有小学数学教师根据教学内容与实践将空间观念分为实物几何化、想象物体的方位和相互之间的位置关系、描述图形运动与变化以及语言理解和几何直观四个方面(15)徐云鸿:《小学高年段空间观念测评体系研究》,《数学教育学报》2019年第5期,第9-13页,第97页。。后续更多的研究一部分关注对学生某一方面能力的测试,另一部分关注对学生空间观念的培养,并没有涉及对学生视觉空间推理能力表现的具体考察。
综上所述,尽管目前对视觉空间推理还没有形成统一的认识,但主要是从心理学和数学视角对其内涵做了界定:心理学中,视觉空间推理是在头脑中形成图像和概念并对这些视觉图像进行改造和分析的心理过程;数学中,视觉空间推理指的是创造性地运用视觉图像来解决数学问题(16)Owens K. Visuospatial Reasoning: An Ecocultural Perspective for Space, Geometry and Measurement Education. Springer. 2014.。由于小学生视觉空间推理能力是视觉空间推理能力在小学数学学习中的体现,我们可以明确小学生视觉空间推理能力是把空间观念和几何推理有机结合起来,基于直观和表象进行推理,解决几何问题(17)孔企平:《从空间观念到视觉空间推理——小学数学课程改革新动向》,《小学教学(数学版)》2019年第9期,第8-12页。。小学生视觉空间推理能力表现指的是学生在几何问题解决过程中,借助几何直观与空间想象相结合的方式,对头脑中形成的表象进行表征的能力,包括两种能力形式:识别和构建视图以及运用视图解决问题。
三、 小学生视觉空间推理能力表现测评框架的探索
(一) 小学生视觉空间推理能力测评维度的构成
基于前面的分析,我们认为小学生视觉空间推理能力的测评维度应体现学生对头脑中形成的有关图形的数学性质的表象进行识别、理解、判断和操作的能力,以及运用图形描述、分析和解决问题的能力。
测评维度的确立经历了两个阶段:首先,基于对已有研究的梳理和分析,结合新一轮课标修订中的一些表述,筛选项目提炼出小学生视觉空间推理能力测评维度的核心要素,编制形成初步的小学生视觉空间推理能力测评维度的调查问卷;其次,采用德尔菲法进行三轮专家意见咨询,根据专家提出的意见不断调整完善,主要包括对含义重叠、上下维度关联性较强的维度进行删除和修改,以及对维度内涵描述部分的语句表述进行修正等。
通过向10位专家发放“小学生视觉空间推理能力测评维度的调查问卷”来咨询专家对测评维度的意见,专家组成员包括小学数学教育专家、小学数学教师和小学数学教研员。对专家的反馈结果进行整理和分析后发现,比较集中认可的维度有两个:一是识别和构建视图;二是运用视图解决问题。其中,识别和构建视图维度认可度较高的有三个方面:图形的展开与折叠、图形的二维与三维转化以及图形的旋转;运用视图解决问题维度认可度较高的有两个方面:空间组合和空间测量。再结合访谈,确认了五个方面的含义及要素如下:
1. 图形的展开与折叠
图形的展开与折叠主要指在图形展开或折叠过程中,对头脑中形成的表象进行判断和操作的能力。“认识一些简单几何体的展开图以及能正确进行几何体与其展开图之间的转化”(18)中华人民共和国教育部:《义务教育数学课程标准(2011年版)》,第18-19页,第23-25页。,这要求学生不仅要了解立体图形和平面图形的基本特征,还要理解二维和三维图形间的差异,能够进行立体图形与平面图形的相互转化。
2. 图形的二维与三维转化
图形的二维与三维转化主要指能从不同方向观察立体图形,形成准确感知视图的能力,并能根据不同方向观察到的视图还原立体图形。“辨认从不同方向看到的几何体的形状、想象出几何体的方位和相互之间的位置关系”,这要求学生针对呈现的立体图形,识别并画出它在不同方向呈现的不同视图,或者根据某个方向看到的视图建立整个立体图形的结构。
3. 图形的旋转
图形的旋转主要指想象平面或立体图形进行旋转后所得到新图形的能力。“识别图形的旋转、画出旋转后的图形,以及能用不同方式描述图形的运动与变化”,这要求学生根据所给平面或立体图形的特征以及旋转概念,通过想象对图形旋转后的状态进行判断,或用适当的方式表示出图形旋转后的状态。而从平面图形旋转得到立体图形,是二维向三维的过渡,学生需要在头脑中清晰界定二维和三维图形间的区别与联系。
4. 空间组合
空间组合主要指能识别立体图形中的基本要素及其关系,从复杂立体图形中分解出基本图形,又能把基本图形组合成复杂立体图形。这对学生空间结构化以及图形分解与组合的能力要求较高,需要在拆解或拼组立体图形的过程中,对形成的表象进行操作和推理,想象或预测即将出现的结果。
5. 空间测量
空间测量主要指根据立体图形表面积与体积的性质建立有关表象,感知立体图形表面积与体积的大小。空间测量是视觉空间推理的重要表现形式,是对图形大小的理解和判断,侧重学生在头脑中建立的有关立体图形表面积与体积的表象,及对表面积和体积实际意义的理解,并不涉及计算,计算属于代数部分。
(二) 小学生视觉空间推理能力表现测评框架的确立
经分析,图形的展开与折叠、图形的二维与三维转化和图形的旋转侧重想象层面,即在头脑中形成有关图形的表象,并对形成的表象进行加工和操作,构造新的表象,是后两个方面的基础。空间组合和空间测量侧重推理层面,即基于表象进行几何抽象和推理,分析和解决问题,是前三个方面的进一步延伸与发展。因此,在综合数学教育专家和一线数学教师的意见后,初步构建了小学生视觉空间推理能力表现的测评框架,包括2个一级维度和5个二级维度,且每个二级维度包括2~3个具体的评价要素。
为探究测评框架构建的合理性,编制了“小学生视觉空间推理能力表现的测评框架调查问卷”,并邀请30位专家(包括小学数学教育专家、小学数学教研员和小学优秀教师)对测评框架进行评价。该问卷采用Likert五级量表形式进行计分,从“非常不同意”到“非常同意”,依次赋分为1~5,得分越高,表明对小学生视觉空间推理能力表现的测评框架越认同,问卷总体信度Cronbach’sα=0.832,统计结果如表2所示。
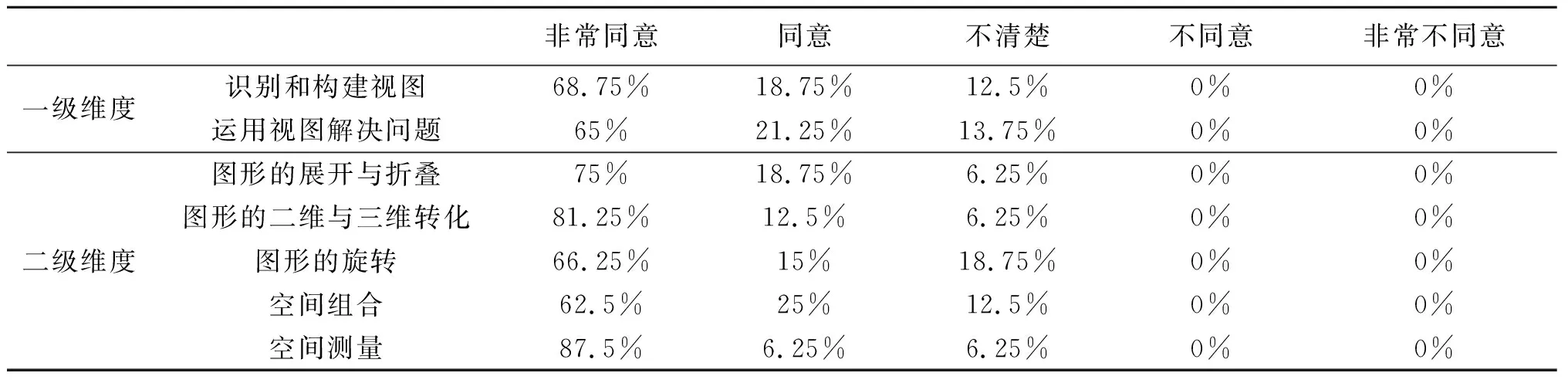
表2 专家对小学生视觉空间推理能力表现测评框架的认同度情况
由表2可知,专家对一级维度的认同度“非常同意”和“同意”之和分别为87.5%、86.25%,对二级维度的认同度“非常同意”和“同意”之和分别为93.75%、93.75%、81.25%、87.5%、93.75%。由此可以判断,专家对小学生视觉空间推理能力表现测评框架的整体认同度较高,此外,与上述群体中部分专家进行访谈的结果也较好地验证了测评框架的科学性。大部分专家认为该测评框架结构设计合理,部分专家认为“基于抽象进行推理对小学生来说难度较高”,应增加“多个图形的位置关系”。也有专家建议二维与三维转化不仅仅是简单地抽象出平面图形或者还原立体图形,还应根据课程标准所提出的要求,增加“考察学生确定搭成立体图形所需要小正方体的数量范围”的评价要素。从这些质性描述可知,该测评框架能有效评价小学生视觉空间推理能力的表现,符合专家们的经验与认知。根据专家们提出的意见进行调整与修改,最终确定小学生视觉空间推理能力表现的测评框架(具体如表3所示)。
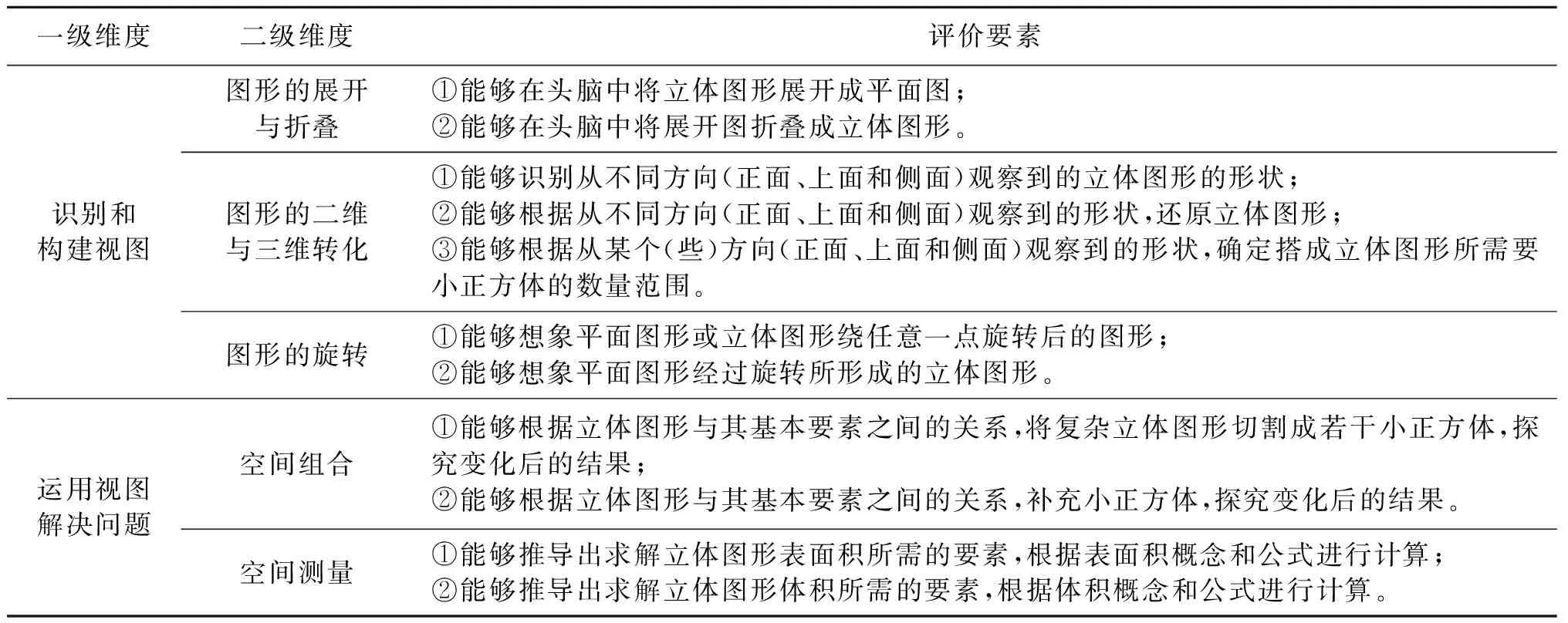
表3 小学生视觉空间推理能力表现的测评框架
四、 小学生视觉空间推理能力表现测评框架的应用
(一) 小学生视觉空间推理能力表现测评工具的编制
测评工具的编制是测评实施的前提条件,它既体现了对视觉空间推理能力内涵的理解,也希望通过题目很好地反映小学生视觉空间推理能力的具体表现。因此,在参阅国内外视觉空间推理相关研究的基础上,对《义务教育数学课程标准(2011年版)》和北师版小学数学教材中图形与几何内容进行深入细致的分析,并按照上述测评框架的维度划分进行问卷的编制。经过与专家三轮的讨论,以及预测试与修改,删除其中5个题目,并对词句不适切的题目进行调整,最终得到一份有16个题项的正式问卷。下面根据每一维度的指向,选出5个具体的样例进行阐述:
【样例1】
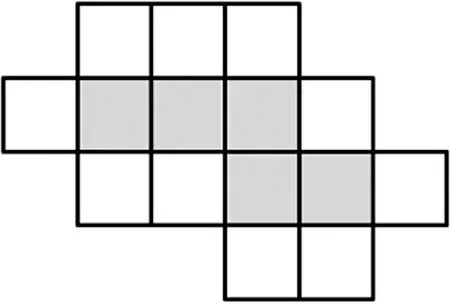
如图所示,从无色的正方形中选出一个,使其与图中5个有色的正方形一起可以折成一个正方体的纸盒。有几种不同的选法?在图中用数字标出来。
设计意图:该题目是在“图形的展开与折叠”上考察学生对正方体及其展开图的理解,以及进行立体图形与平面图形相互转化的能力。学生需要根据题目所给的线索准确识别出能折成正方体的小正方形,在头脑中操作展开图以形成正方体的表象。此外,学生还需要掌握正方体的11种展开图。
【样例2】
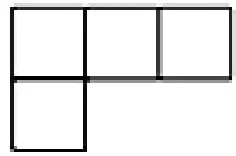
设计意图:该题目是在“图形的二维与三维转化”上考察学生由不同方向视图想象和还原立体图形的能力,让学生的思维经历从二维到三维的过程。不仅要有一定的空间想象力,还要具备解决此类问题所用的方法,即在由三视图构建立体图形结构时,要先看俯视图,在此基础上采用加法策略想象哪个位置上方有小正方体,进一步体会根据从两个方向看到的视图并不能确定唯一一个立体图形,而是会有不同的情况。
【样例3】
一张纸片被一个图钉固定在桌面上,可以绕图钉旋转这个纸片。下面哪个图形是纸片绕图钉旋转后得到的?( )

设计意图:该题目是在“图形的旋转”上考察学生对平面图形旋转后状态的判断。需要改变观察的位置或在头脑中感知并形成图形运动的表象,以判断图形在平面上经过旋转后能否与自身重合,对学生空间想象力的要求大于对旋转概念的理解。
【样例4】
笑笑想利用1cm3的小正方体做一个积木模型(如图),并在积木模型的表面涂上颜色。

(1) 有一面、两面、三面被涂上颜色的小正方体各有多少个?
(2) 有多少个小正方体六个面都没有涂上颜色?
设计意图:该题目是在“空间组合”上考察学生将三维空间的“体”抽象成二维空间的“面”的能力,需在建立3×3×5长方体表象的基础上,探寻表面涂色的规律。解决涂色问题学生需要经历“想象—分解—还原—分类”的过程:想象是通过对立体图形的观察想象出各个面的平面图形;分解是要清楚每个面的平面图形是由哪些小正方形组成;还原是在想象和分解的基础上,观察每个小正方形所在的小正方体,以及这个小正方体所在长方体的位置;分类是基于想象、分解和还原,计算不同位置的小正方体各有多少个。而没有涂色的小正方体需要将每个面逐层剥离所得,侧重考察学生空间结构化的能力。
【样例5】
笑笑买了一套故事书(上、下两册)送给好朋友,每本书长26cm,宽18cm,厚1cm,如果要将这套故事书包起来,至少需要多大面积的包装纸?
设计意图:该题目是在“空间测量”上考察学生对表面积概念和意义的理解,以及能否根据语言描述将实际问题抽象为数学问题。学生需要清楚求“至少需要多大面积的包装纸”实际上就是求长方体各个面的面积和,根据题目描述抽象出故事书这个长方体表象,用表面积概念去思考和探索应如何叠放长方体,以推导出新长方体的长、宽、高,并运用公式解决问题。
(二) 小学生视觉空间推理能力表现测评结果分析
为了解小学高年学生视觉空间推理能力的具体表现,本研究以问卷形式对小学六年级学生进行调查,选取长春市S小学六年级6个班学生进行正式测试,共发放问卷225份,其中有效问卷210份,有效回收率为93.34%。对问卷进行信、效度检验,结果如下:KMO=0.824,Bartlett球形检验p=0.000<0.001,这表明各变量间相关程度较高,可以做探索性因子分析。问卷总体信度Cronbach’s α=0.861,具体五个维度的信度水平详见表4。通过信度检验,问卷的信度指标有了明显的改善,各个维度之间具有较高的一致性,可以作为研究工具使用。

表4 正式问卷信度分析表
经测试结果统计分析,学生视觉空间推理能力的整体均值为23.96(总分为40分),得分较低,才达到总分的一半。对学生视觉空间推理能力进行描述性分析,结果如表5所示:

表5 小学六年级学生视觉空间推理能力表现描述统计分析
由表5可知,六年级学生已具备一定的视觉空间推理能力,但在不同维度上的能力表现有所差异。得分均值由高到低排序为:图形的旋转、图形的二维与三维转化、图形的展开与折叠、空间组合、空间测量。图形的旋转维度均值为5.65,较其他维度表现略好。空间测量维度均值偏低为3.90,较其他维度表现不佳。这表明基于表象进行抽象和推理对小学生来说难度还是较大的,因为这不仅涉及将视觉和空间的想法具体地在大脑中呈现出来,还需要借助几何直观与空间想象相结合的方式,利用视图进行几何抽象和推理。
(三) 小学生视觉空间推理能力表现测评框架的使用
经上述分析可以得出,按照测评框架编制的问卷能在大范围内进行测试,具有可操作性,能反映小学生在视觉空间推理能力不同维度上的具体表现,可以为教师评价学生的视觉空间推理能力提供参考,但是,教师在运用时应注意该测评框架适用于小学高年级学生(5—6年级)。同时,构建小学生视觉空间推理能力表现测评框架的主要目的是为教师如何发展和评价学生的视觉空间推理能力提供参考,以促进教师改进教学方式,因此,可与单元学习评估、日常练习等其他评价方法结合起来使用,或在课堂教学过程中进行即时评价,以更好地促进小学生视觉空间推理能力的发展。
