可移动月球着陆器系统设计与实验验证

贾 山，周向华，陈金宝，王永滨,4，赵建华，张 胜

（1.南京航空航天大学 航天学院，南京 211106；2.航天进入减速与着陆技术实验室，南京 211106；3.深空星表探测机构技术工信部重点实验室，南京 211106；4.北京空间机电研究所，北京 100094）

引 言

重返月球和载人火星探测并列为21世纪深空探测的两大目标，其中，着陆器在相关任务中发挥了至关重要的作用。目前，已实施和正在实施的星表探测任务中，着陆器均不具备自主运动能力，即着陆器着陆后姿态、位置均为固定[1-4]。固定式着陆的有效性已多次在探测任务中得到检验，且可通过搭载轮式巡视器扩大探测范围，但仍存在一定的局限性，例如扩展范围和巡视器功能有限等。着陆器无法调姿和移动，在综合考虑着陆过程安全性和科学目标达成性的情况下，明显限制了着陆点的选择，从而导致探测范围受限和缓冲进程无法统一。此外，无法调姿和移动的着陆器对未来星表基地建设等任务的适用性有限，需引入专用运输工具承担物资转运、人员运输、居住舱连接等工作，将会显著增加发射载荷和任务成本。因此，设计一种缓冲/行走一体化腿足式着陆器，在悬臂式构型的基础上，融合缓冲吸能和主动驱动的功能，使其能够在吸收巨大冲击载荷的同时实现灵活的星表漫游，将具有明显的工程实用价值。

目前，国内外对可移动着陆器只进行了一些探索性的研究与设想。文献[5]提出了基于ALTHETE的轮腿式可移动着陆器，该着陆器具备六条轮腿式腿足，可实现月面快速移动和姿态调整，多个着陆器还可对接组合形成月球基地；文献[6]提出了一种轮式货运着陆器，可在星表移动并承担人员居住和增压任务；文献[7]提出了一种星表着陆器，其上升级配置轮式移动系统，可单独完成着陆并在月表移动；文献[8]提出了一种轮腿式可移动月面着陆器，采用六足构型，单腿具备3个自由度，可实现月面行进和障碍攀爬。以上研究均为设想，且均未考虑腿足机构缓冲功能的实现。文献[9-10]提出了一种腿足式可移动着陆器，并针对其软着陆和行走功能进行了多学科拓扑优化，但未对行走步态进行设计；文献[11]提出了一种用于着陆探测的四足机器人并设计了行走步态，但未考虑缓冲功能实现；文献[12]提出了一种星表探测六足轮腿组合式机器人，可切换运动模式实现腿足移动和轮式驱动。以上研究均为仿真分析，未进行样机试验。可移动着陆器虽未有成功案例，但腿足式机器人已发展了数十年，积累了较为丰富的研究成果[13-15]。相比于轮式机器人，腿足式机器人有着优秀的地形适应性和通过性；相比于多足机器人，四足机器人质量轻、体积小，发射成本低；相比于轮腿式机器人，腿足式机器人不易打滑，抗冲击能力更强；相比于串联式腿足构型，并联式构型有着负载能力强的特点[16-18]。因此，四足并联腿足构型成为兼顾移动性和稳定性的可移动着陆器的最佳构型。

为实现可移动着陆器在非确知、非结构性星表环境下的灵活漫游，需要进行步态设计。步态设计可分为动态步态和静态步态。由于星表移动任务首先需保证安全性和稳定性，可移动着陆器的运动过程较为缓慢，惯性力的影响微弱，可采用静态Walk步态。文献[19]和文献[20]中分别采用间歇步态和爬行步态对四足机器人进行了运动轨迹规划，两种步态均属于静步态，具有较高的行走稳定性。文献[21]采用COG轨迹规划法设计了行走步态，增强了步态的稳定性；文献[22]和文献[23]分别采用离线规划法和神经网络算法规划了四足机器人的行走步态。以上步态均为动步态，具有较高的移动速度但稳定性低于静步态。因此，本文将设计典型静步态Walk步态，用于实现着陆器的行走与转弯动作。在步态设计中，需要对可移动着陆器的足端迈步轨迹进行规划，避免足端与地面产生碰撞或者在迈步开始和结束时发生冲击。文献[24]采用了轨迹组合方法来规划机器人足端的运动轨迹，使得机器人足端轨迹的起始点和终止点速度、加速度均为零值；文献[25]采用参数优化的多项式轨迹法规划了机械臂的运动轨迹；文献[26-27]采用B样条曲线对并联机器人运动轨迹进行了规划，保证了轨迹初始和最终速度为零；文[28]采用摆线法规划了机器人的三角步态，得到了稳定连续的运动轨迹。本文所提着陆器对速度要求较低，且迈步时间较长，同时，样条曲线和组合轨迹的方式占用过多计算时间，故本文采用抛物曲线进行轨迹规划，在节省计算时间的同时，还方便调节迈步参数。

综上，本文提出了一种新型可移动着陆器，并进行了整器系统设计；介绍了可变构型式主体和吸能/驱动集成式缓冲器的功能及实现方式；建立着陆器运动学模型的基础上，进行了静步态规划和足端运动轨迹规划，并进行了虚拟样机仿真；最后，进行了实物样机实验，校验了系统设计的合理性和步态规划的有效性。

1 整器系统设计

本文所设计的可移动月球着陆器系统主要由本体主承力结构子系统、构型转换子系统、吸能/驱动集成式腿足子系统和运动控制子系统等部分组成。本体主承力结构子系统负责构成着陆器本体，为其余子系统和科学载荷提供支撑与安装平台；构型转换子系统用于实现可移动着陆器着陆姿态与行走姿态的切换，以及收拢状态与展开状态的切换；吸能/驱动集成式腿足子系统用于实现软着陆和星表移动；运动控制子系统负责为星表移动任务提供步态规划与腿足运动控制。区别于传统不可移动式着陆器，可移动着陆器通过构型转换子系统，将着陆器由着陆姿态（腿足呈四足均布式）转换为行走姿态（腿足呈前膝后肘式），提高了着陆器的移动效率；通过吸能/驱动集成式腿足子系统，使腿足机构在保证着陆器实现缓冲功能的同时，具备移动能力。可移动月球着陆器系统设计架构如图1所示，各子系统任务和主要功能如表1所示。

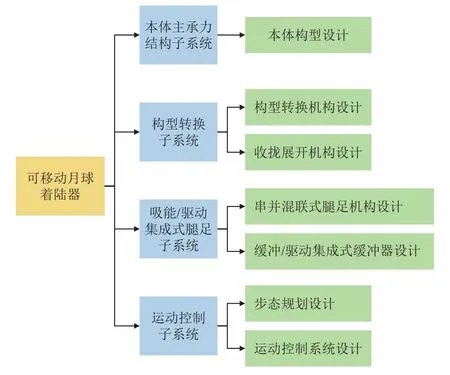
图1 可移动月球着陆器系统设计架构Fig.1 System design architecture of mobile lunar lander

表1 子系统任务和主要功能Table 1 Tasks and major functions of the subsystem

2 整器设计方案的创新性

2.1 可变构型主体设计

可移动月球着陆器具备着陆缓冲和星表移动功能，由本体和4组3自由度串并混联式着陆腿组成。串并混联式着陆腿不但具有并联构型的大承载能力，同时具有串联构型的运动灵活性，能够满足可移动着陆器的缓冲与移动功能需要。每条着陆腿均包含1组主缓冲器、2组辅助缓冲器、1条推杆、1条腿杆和1个足垫，具有3个移动自由度，对应1个转动关节和1个万向节，每个关节处均装有旋转编码器。初始状态下，可移动月球着陆器处于缓冲状态，4条着陆腿均布于本体四周，完成缓冲着陆后，由构型转换机构驱动，着陆器采用三足支撑，一足转换的方式，通过调整着陆器姿态，依照“左前—右前—右后—左后”的顺序完成腿足机构由四足均布式向前膝后肘式的转换，由于构型转换的调姿规划与运动控制不是本文重点，这里不作赘述。着陆器转变为行走状态，4条着陆腿两两对称分布于本体两侧，如图2所示。辅助缓冲器与本体连接处装有收拢展开机构，可通过向上滑动实现着陆腿收拢，向下滑动实现着陆腿展开与锁定，如图3所示。

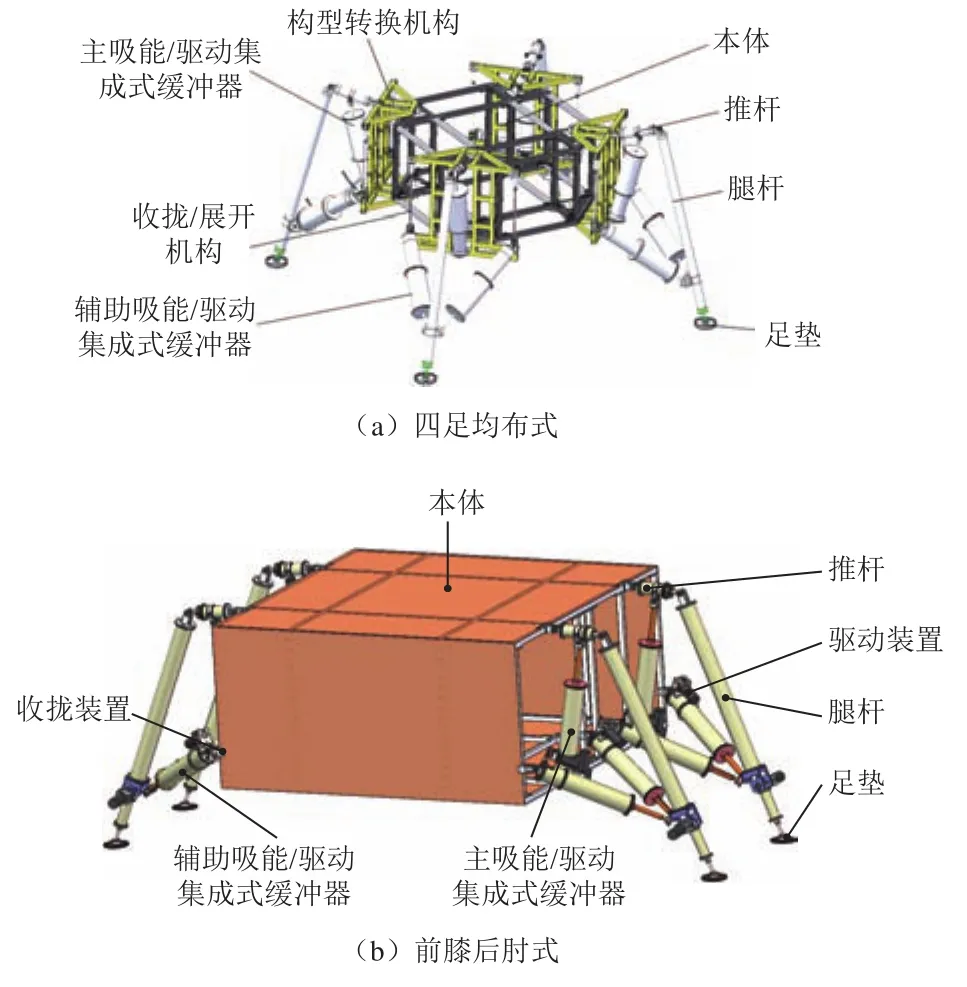
图2 可移动月球着陆器Fig.2 Mobile lunar lander

图3 可移动月球着陆器收拢与展开状态Fig.3 Collapsed state and expanded state of mobile lunar lander

2.2 吸能/驱动集成式缓冲器设计

吸能/驱动集成式缓冲器用以实现缓冲和行走功能[29]。该缓冲器主要由外筒、内筒、活塞杆、缓冲吸能材料和驱动装置组成，如图4所示。缓冲器内筒和外筒之间分别放置铝蜂窝材料，可进行双向拉压缓冲吸能；驱动装置由直流伺服电机、减速器、制动器和滚珠丝杠组成，滚珠丝杠与缓冲器活塞杆相连，通过电机转动带动滚珠丝杠运动，可实现活塞杆相对于内外筒主体部分的伸缩运动，进而实现腿足机构的迈步等运动。缓冲/行走功能切换由切换装置实现，缓冲状态下，卡锁与卡槽保持分离，此时缓冲器具备双向拉压缓冲能力，可作为主/辅助缓冲器吸收着陆过程中的纵向和侧向冲击载荷；缓冲任务完成后，丝杠带动滑块运动，实现卡锁与滑块的锁止，随后活塞杆与丝杠螺母保持固定，通过滚珠丝杠转动，可实现缓冲器活塞杆的伸缩移动，从而作为主/辅助缓冲支柱的驱动机构驱动着陆腿完成规定动作。

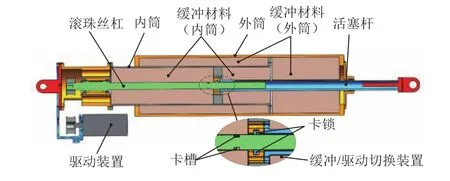
图4 吸能/驱动集成式缓冲器Fig.4 Energy-absorbing/Driving integrated buffer

吸能/驱动集成式缓冲器内部选用串联式三级铝蜂窝组合结构，可降低着陆过程中的反向加速度峰值。采用H004-3 003（弱）、H005-3 003（中）、H005-5 052（强）3种型号铝蜂窝串联，设定落震本体质量为300 kg，以模拟1/4着陆器；铝蜂窝长度为360 mm，触地速度为4m/s，用于模拟铝蜂窝溃缩力的活塞滑块与筒壁的接触动静摩擦系数均为0.3。仿真过程中，弱、中、强3种铝蜂窝依次溃缩吸能，本体反向加速度曲线如图5所示，最大过载低于5.5 g。设计与仿真过程详见文献[30]。

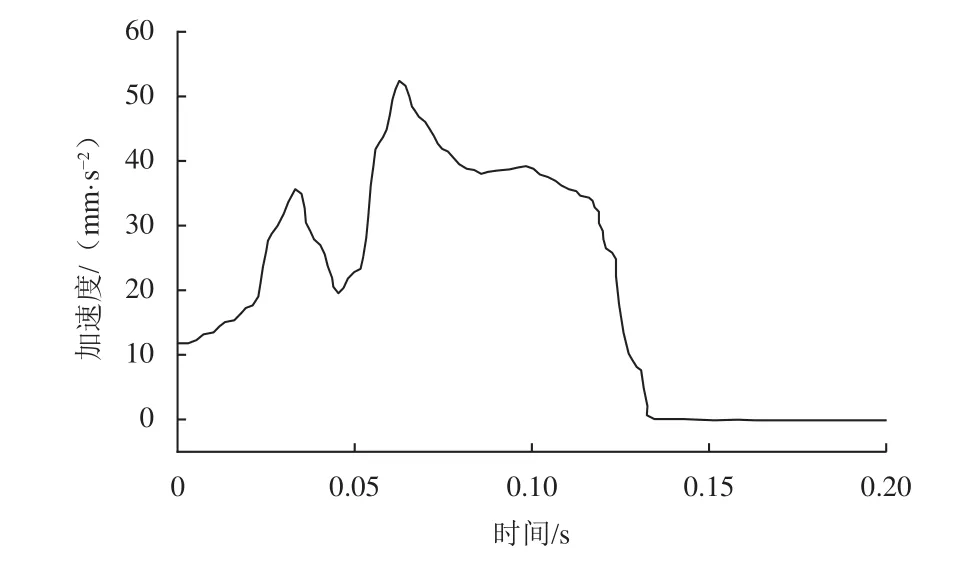
图5 串联式三级铝蜂窝反向加速度曲线[30]Fig.5 Reverse acceleration curve of serial three-stage aluminium honeycomb[30]

3 步态系统设计与仿真

3.1 腿足机构运动学模型

建立可移动着陆器坐标系如图6所示。在推杆与着陆器本体的4个连接点处依次建立腿足坐标系{OLF}、{OLB}、{ORF}、{ORB}，在该点所在平面几何中心建立机体坐标系{OB}，如图6（a）所示，腿足各部分参数定义如图6（b）所示。以腿足RF为例，建立单腿关节坐标系[31-33]，以推杆与着陆器本体连接点处转动关节R3为原点建立腿足坐标系{O1}，以推杆与腿杆连接处胡克铰U3为原点建立坐标系{O2}和{O3}，以腿杆与足垫连接处建立坐标系{O4}。

图6 着陆器坐标系示意图Fig.6 Coordinates of lander

根据上述关节坐标系定义，令坐标系{O1}、{O2}和{O3}处的关节转角对应为θ1、θ2和θ3。推杆长度为L1，腿杆长度为L2，主缓冲支柱初始长度为C1，辅助缓冲支柱初始长度分别为C2和C3。根据连杆参数关系，由改进D-H参数法建立单腿连杆参数表[33]，如表2所示。

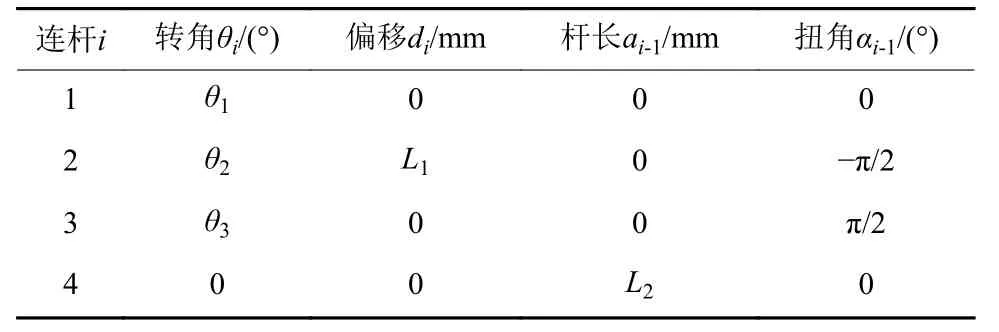
表2 单腿机构连杆参数表Table 2 Link parameters of single leg

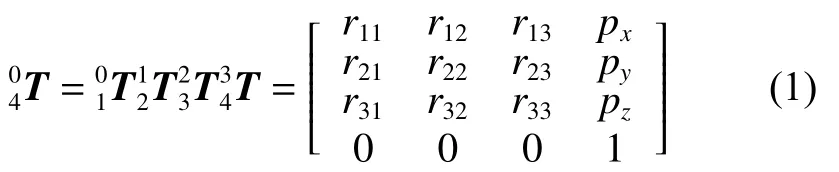
其中

进一步，通过分离θ1项至等式（1）的左边，可得式（3）所示方程式

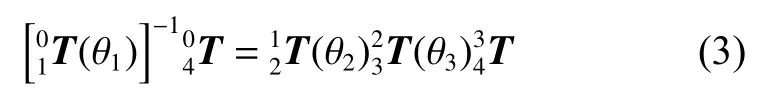
由于连杆变换矩阵T的旋转矩阵正交且不含平移分量，其逆矩阵等于转置矩阵，因此将式（3）改为式（4）形式

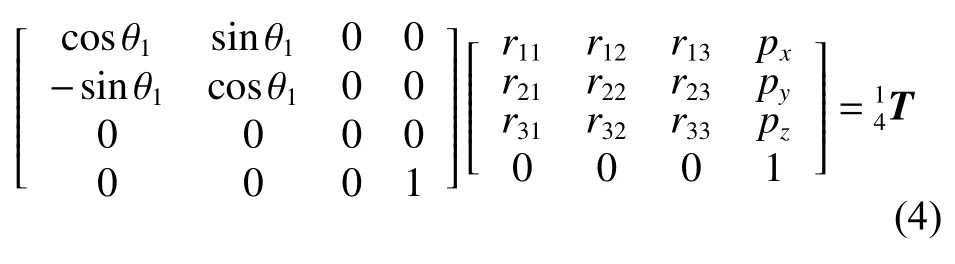
令等式（4）两边对应元素(1,4)、(3,4)项分别相等可得式（5）

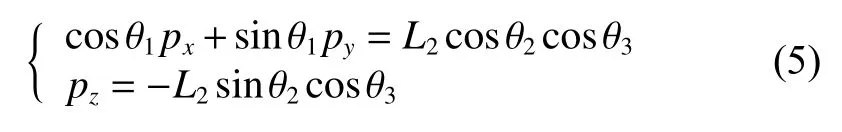
对式（5）方程组求解得到运动学逆解如式（6）所示

主/辅助缓冲支柱的伸缩位移可由转动关节向驱动关节的映射得到。转动关节R1、R2、R3和主缓冲支柱P1构成封闭三角形如图7所示。由余弦定理可得，主缓冲支柱P1的伸缩位移p1与关节转角θ1的关系如式（7）

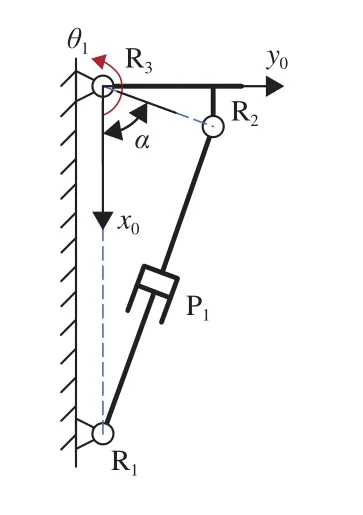
图7 封闭三角形几何映射关系Fig.7 Closed triangle geometric mapping relationship

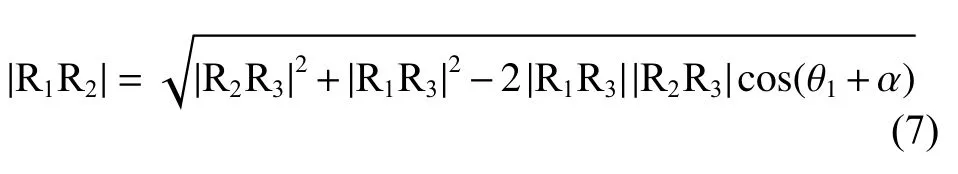
辅助缓冲支柱的伸缩位移可由胡克铰U3处的关节转角θ2和θ3映射得到。设胡克铰U1、U2在坐标系{ORF}内坐标为(xU1,yU1,zU1)、(xU2,yU2,zU2)，球铰S1、S2在坐标系{O3}内坐标为(a,−b,c)、(a,−b,−c)。在坐标系{ORF}内，球铰S1、S2的位置坐标(xS1,yS1,zS1)、(xS2,yS2,zS2)可由正运动学推导得到，如式（8）～（9）。由球铰S1、S2的位置关系可求得辅助缓冲支柱P2、P3的伸缩位移p2、p3与关节转角θ1、θ2、θ3之间的关系如式（10）～（11）。

3.2 迈步顺序设计

腿足处于支撑相的时间占单个步态周期时间的比值称为占空比β，根据占空比的不同，四足行走步态可分为静步态（0.75≤β＜1）和动步态（0＜β＜0.75）。为保证着陆器的行走稳定性和高负载性，本文选用连续静步态规划，并令占空比β=0.8，静步态规划中，为保持着陆器运动稳定，需进行姿态调整。同时，静步态因其高占空比导致了移动速度缓慢，为此，需通过减少行走步态中调姿次数来提高其移动速度。

静步态规划中，有6种步态可保持着陆器占空比β>0.75，如图8所示，其中只有3种可保持着陆器的静态稳定性，如图8（d）、图8（e）和图8（f）。在图8（d）所示迈步顺序中，着陆器需完成4次本体调姿才可依次实现4条腿足迈步；图8（e）和图8（f）中，着陆器如采用前后调姿法，则可将调姿次数缩短为2次，即1次调姿实现2条腿足迈步。因此，选用图8（e）所示迈步顺序进行直行和右转弯步态规划，选用图8（f）所示迈步顺序进行左转弯步态规划，调姿方向均为前后调姿。

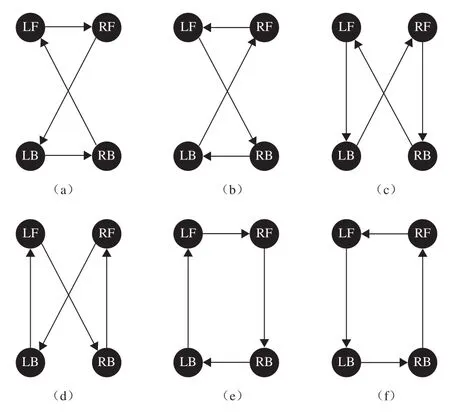
图8 6种静步态迈步顺序Fig.8 Step sequence of 6 kinds of static gait

着陆器直行过程中各腿足机构的运动时序如图9所示。其中，支撑相表示腿足处于支撑状态且构成支撑三角形，摆动相表示腿足处于迈步状态，此时着陆器处于迈步状态；扩展支撑相表示腿足处于支撑状态并构成支撑四边形，此时着陆器处于调姿状态。着陆器在前进和右转弯步态中，以“调姿—左前腿足迈步—右前腿足迈步—调姿—右后腿足迈步—左后腿足迈步—调姿”为周期序列；左转弯步态中，以“调姿—右前腿足迈步—左前腿足迈步—调姿—左后腿足迈步—右后腿足迈步—调姿”为周期序列。

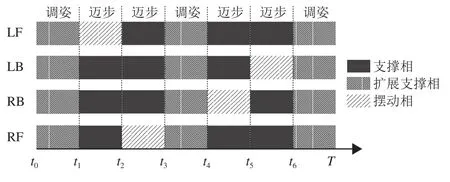
图9 静步态序列图Fig.9 Static gait sequence

图10为静步态行走示意图，着陆器直行步态初始状态如图10（a）所示，其中，正方形为着陆器本体，其质心位于本体几何中心，4个圆表示足垫末端位置，其中黑色表示支撑相，灰色表示摆动相；着陆器向前运动时，着陆器本体需向后调姿，如图10（b）所示；之后，腿足LF向前迈步，此时着陆器本体质心位于腿足RF、LB和RB组成的支撑三角形内，着陆器处于稳定状态，如图10（c）所示；然后，腿足RF向前迈步，同理，着陆器处于稳定状态，如图10（d）所示；再次，着陆器各腿足处于支撑相，着陆器本体向前调姿，如图10（e）所示；然后，腿足RB和LB相继迈步，着陆器本体均处于稳定状态，如图10（f）和10（g）所示；最后，着陆器本体向后调姿回到初始状态，此时着陆器完成向前运动的一个步态周期，如图10（h）。

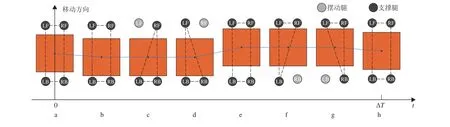
图10 四足直行步态示意图Fig.10 Walking gait

着陆器转弯步态（以右转弯为例）与行走步态相似，只在各腿足迈步和中间调姿过程中存在差异，具体如图11所示。着陆器本体向后调姿后，腿足LF向右前方迈步，此时腿足RF、RB和LB构成稳定三角形，如图11(c)所示；然后，腿足RF向右前方迈步，腿足LF、LB和RB构成稳定三角形，如图11（d）所示；然后着陆器本体向前调姿并向右转弯，如图11（e）所示；之后，腿足RB、LB分别向左前方迈步，如图11（f）、11（g）所示；最后着陆器本体向后调姿回到初始位置，如图11（h）所示。

图11 四足转弯步态示意图Fig.11 Turning gait

3.3 足端轨迹设计

根据着陆器行走及转弯步态设计，其足端轨迹规划可分为调姿轨迹和迈步轨迹。当着陆器腿足在地面处于支撑相时，足端轨迹保持不变；当腿足处于扩展支撑相时，足端轨迹为调姿轨迹；当腿足处于摆动相时，足端轨迹为迈步轨迹。着陆器调姿过程中，腿足与地面保持不变，着陆器本体相对于地面移动，此时调姿轨迹为足端相对于本体移动的一条直线。由于着陆器移动速度较低，迈步时间较长，故足端离地和落地时，其速度与加速度突变值较小，不会引起着陆器腿足机构的剧烈振动和碰撞。因此，在忽略速度、加速度影响的情况下，本文采用方便调节迈步参数的抛物曲线对上述各种足端轨迹进行描述，如图12所示，其轨迹定义如下

图12 足端轨迹规划示意图Fig.12 Trajectory planning of foot-end

其中：x(t)、y(t)、z(t)为足端在机体坐标系{OB}下的位移变化量；xF、yF、zF为足端在机体坐标系下的位置量；s为迈步步长；h为迈步高度；B1、B2、B3为迈步调节因子，可以通过修改B1、B2、B3的值来调节单个迈步轨迹所耗时间。当足端为迈步轨迹时，x(t)、y(t)、z(t)均发生变化；当足端为调姿轨迹时，步高h为0，x(t)分量不变、y(t)、z(t)发生变化。

3.4 步态仿真与分析

为验证步态设计的有效性，采用Adams进行了仿真。着陆器质量为1 200 kg，设定重力加速度为1.63 m/s2，设定着陆器步态周期为4 s，步距为40 mm，步高为60 mm，其各部分质量参数如表3所示。

表3 着陆器各部分质量参数Table 3 Mass parameters of the lander

根据着陆器足端轨迹和步态设计求解得到各腿足末端相对机体坐标系的“位移—时间”序列后，通过运动学逆解与映射求解得到各驱动关节（主/辅助缓冲支柱）的“位移—时间”序列，图13为直行步态中各腿足驱动关节的位移曲线，可以看出，各驱动所设计的“位移—时间”曲线平顺呈周期变化，主支柱行程为−38～45 mm，辅助支柱行程为−30～32 mm。着陆器行走步态中，着陆器本体沿移动方向调姿，θ2关节未发生转动，故表现为辅助支柱P2和P3“位移—时间”曲线一致。

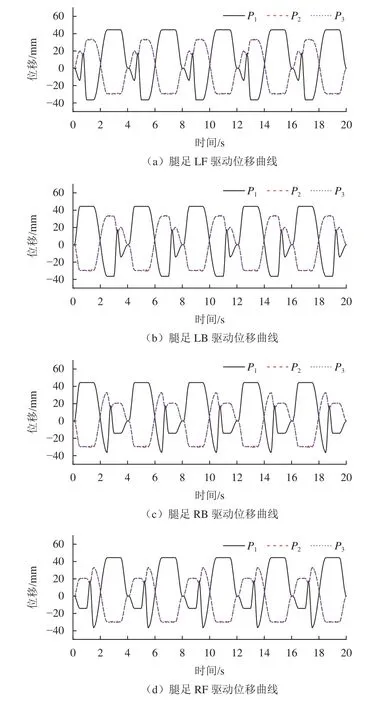
图13 行走步态驱动位移时间曲线Fig.13 Driver’s displacement-time curve of walking gait

之后，将各驱动关节的“位移—时间”曲线作为仿真输入，可得着陆器行走步态和转弯步态仿真如图14和图15所示。可以看出，各腿足迈步顺序与所规划步态序列一致，本体质心沿移动方向变化并始终处于支撑多边形内。

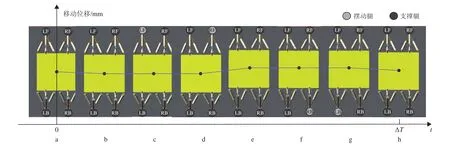
图14 四足直行仿真示意图Fig.14 Simulation of walking gait

图15 四足转弯仿真示意图Fig.15 Simulation of turning gait

着陆器步态仿真过程中，本体质心位移曲线如图16所示。可以看出，行走和转弯步态中，本体质心沿Z方向均无明显波动与偏移，其中，转弯步态Z方向波动逐步增大是由于测量坐标系为地面坐标系，着陆器在转弯步态中Z方向位移分量逐步增大，因此表现为Z方向波动增大。本体质心沿X方向存在上下波动，波动位移约为45 mm，即本体上下起伏较小，起伏量约占本体高度的3.44%。本体质心沿Y方向位移中，行走步态因存在调姿与移动呈波动式增长，此时，着陆器行走速度约为0.01 m/s，转弯步态因存在调姿呈周期式波动。

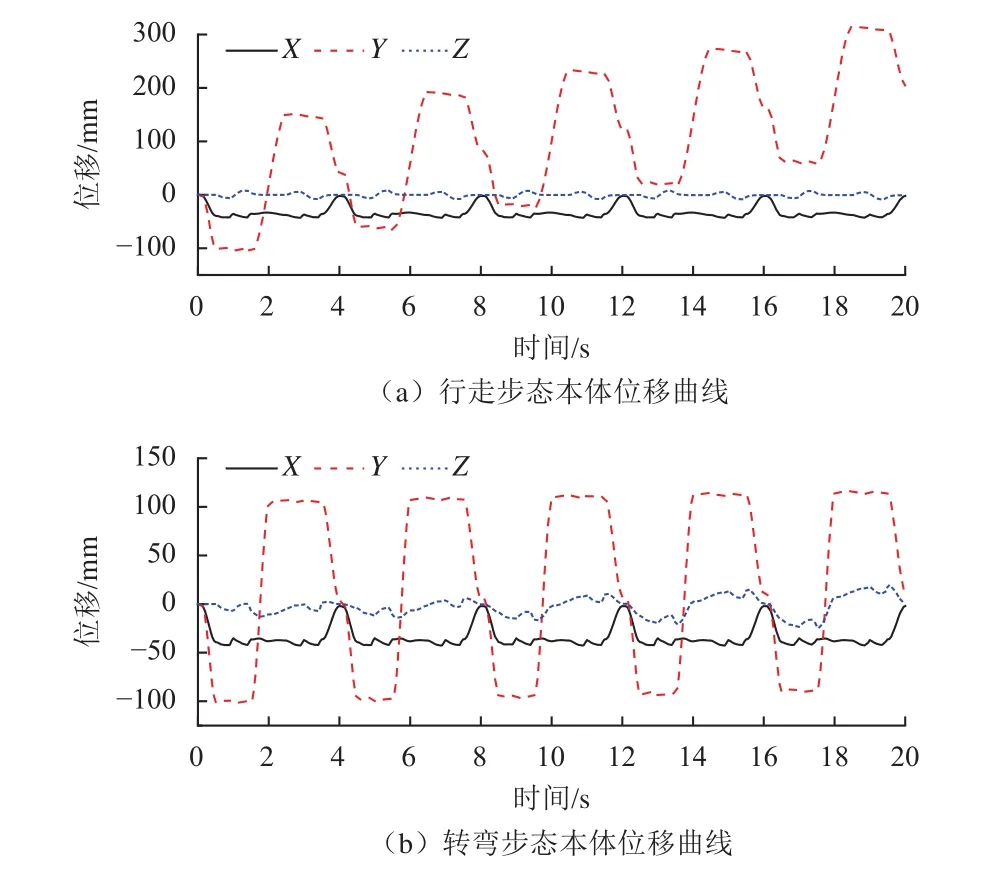
图16 本体质心位移曲线图Fig.16 Displacement-time curve of centre of mass

本体质心姿态变化曲线如图17所示。行走步态中，着陆器本体俯仰角、偏航角和滚转角无较大偏移，均维持在0°左右，上下波动均未超过0.8°。转弯步态中，着陆器本体俯仰角和滚转角均无较大偏移，偏航角因转弯呈阶跃式增长，转弯速度约为0.6 °/s，即转弯90°约需150 s。

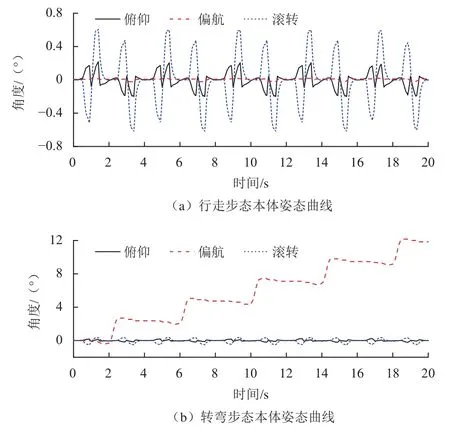
图17 本体姿态曲线图Fig.17 Posture angle of body

着陆器整机功耗曲线如图18所示。单个步态周期中，着陆器瞬时最大功率为600 W，平均负载功率为89.83 W。目前深空探测任务中，小天体探测器采用太阳能电池阵与蓄电池组合的方法，输出功率可达数百瓦甚至数千瓦，星表着陆器采用放射性同位素电池，输出功率可达300 W[35]。因此，着陆器功耗满足一般航天器供电要求。

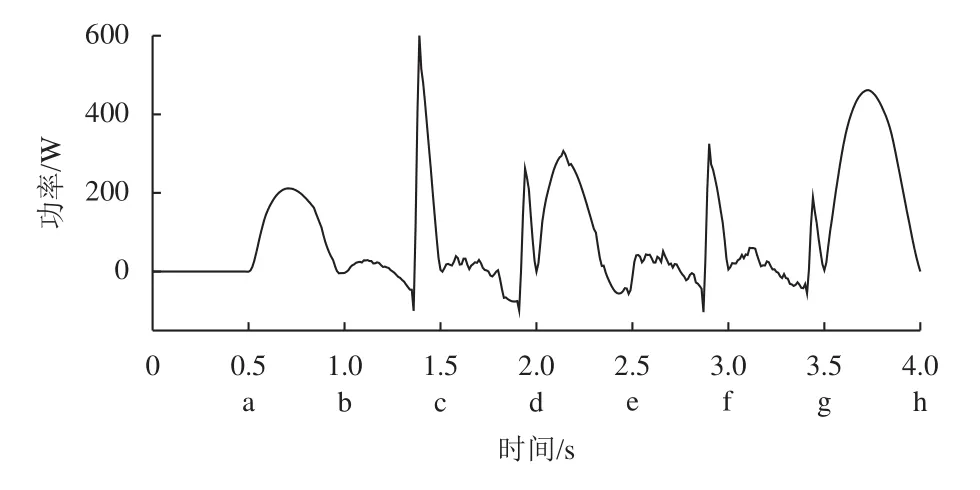
图18 单个步态周期内整器功耗Fig.18 Power consumption of the whole device in single gait period

4 实验验证

研制的可移动月球着陆器试验样机如图19所示。试验样机本体尺寸为1 600×1 600×680 mm，样机高度为1 295 mm，整机质量约200 kg。

图19 可移动月球着陆器样机Fig.19 Prototype of mobile lunar lander

结构部分整机均采用硬质铝合金，部分承力件与传动件为钢件。驱动部分选用直流无刷电机，配合减速器、制动器和编码器实现旋转角度的精确控制。传动部分选用同步带带动滚珠丝杠传动，丝杠螺距为5 mm，单条着陆腿有效推力可达44 kN。各部件具体性能参数如表4～5所示。

表4 直流电机性能参数表Table 4 Performance parameters of DC-motor

表5 减速器性能参数表Table 5 Performance parameters of reducer

控制部分采用FPGA控制器，负责步态规划与解算、腿足闭环控制、传感器信息处理以及与地面站交换数据等工作，其原理如图20所示。

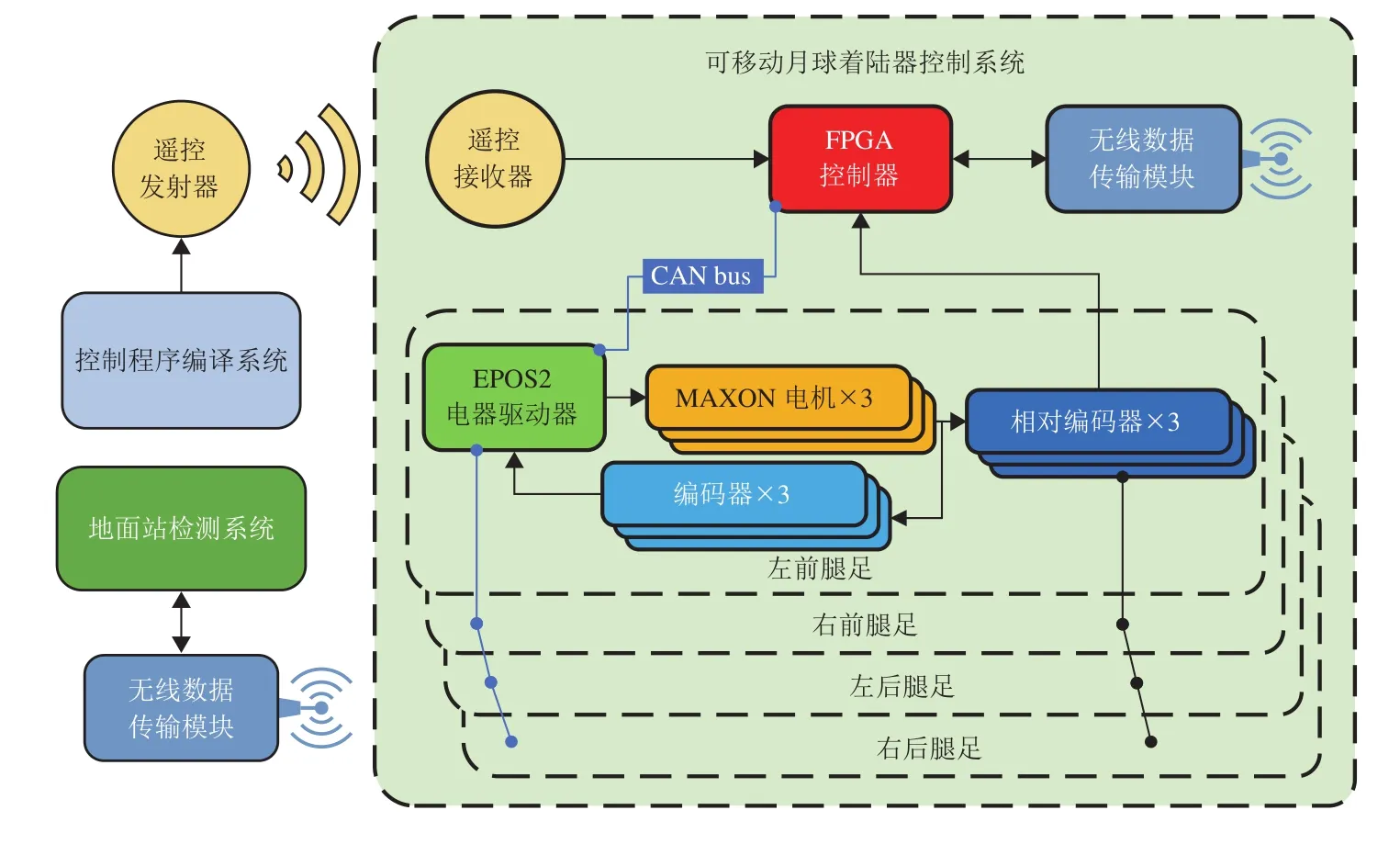
图20 可移动月球着陆器控制系统Fig.20 Control system of mobile lunar lander

为配合地面行走试验，搭建样机地面试验系统如图21所示。为测试可移动着陆器控制系统及步态算法的可行性，编写控制系统上位机软件，通过地面站发送上位机软件指令对着陆器进行初始化配置，之后通过遥控器发送操作指令，着陆器即可依据指令进行移动。

图21 样机地面试验系统Fig.21 Ground test system of prototype

基于研制的可移动月球着陆器样机和相应试验辅助装置进行了Walk步态实验。在悬吊装置的保护下，对样机开展了水平路面行走实验，实验过程如图22所示。为保证行走安全可靠及数据采集有效，将单个步态周期耗时调整为14 min左右，行走结果表明：平均每个步态周期向前实际移动72 mm，着陆器整机移动过程中无较大抖动与偏移。

图22 样机地面行走实验Fig.22 Ground walking test of prototype

5 结 论

本文提出了一种兼具缓冲与行走功能的新型着陆器，进行了整器系统设计、步态设计、虚拟样机仿真以及地面行走试验。首先，介绍了着陆器系统设计，并对可变构型式主体和缓冲/驱动集成式缓冲器的功能实现进行了介绍；其次，在着陆器3自由度腿足运动学模型的基础上，进行了减少调姿次数的直行和转弯的静步态规划，设计了足端迈步与调姿轨迹。最后，对该着陆器进行了虚拟样机仿真及地面行走试验。结果表明：可移动着陆器运动学模型建立正确，规划的驱动位移时间曲线合理；腿足机构运动平顺，可实现行走转弯步态；行走转弯步态稳定，均无较大偏移，本体起伏约45 mm；行走步态中，着陆器移动速度约为0.01 m/s，姿态角波动均未超过1°，转弯步态中，着陆器转弯速度约为0.6°/s，俯仰角和滚转角波动均未超过1°。综上，本文研究成果可为可移动着陆器研究提供一定的设计参考。