预应力混凝土T梁裂缝模拟分析

2022-04-15安定宇

黑龙江交通科技 2022年2期

关键词：梁体本构挠度

安定宇

(山西省交通新技术发展有限公司，山西太原 030012)

1 工程概况及建模

1.1 工程概况

本项目采用预应力混凝土T梁，桥梁总长1 609 m，最高桥墩28 m，共设置40跨，宽24.5 m。公路主线与干流交叉处流域面积约5 918 km2。

1.2 有限元模型

本次建模混凝土模型采用SOLID65实体单元，钢筋采用LINK8杆单元。混凝土模拟采用SOLID65单元，相比SOLID45单元更适合非线性材料的模拟，因此具备了模拟混凝土断裂和压碎的功能，方便对各阶段梁体的受力情况进行分析。采用LINK8杆单元进行钢筋模拟，LINK8杆单元适用于连杆、缆索、钢筋等的模拟。[1]

1.3 材料本构关系建立

(1)混凝土本构

混凝土作为工程中使用最广的材料，成分复杂多样，本构关系也较为复杂。目前混凝土材料的本构关系主要是基于弹性理论或弹塑性理论。其中基于弹性理论的关系虽然方便计算，但往往仅适用处于弹性状态的混凝土研究，而要研究混凝土T梁的受力及开裂情况，因此选择基于弹塑性理论的本构关系。[2]在建模时，运用多线性等向强化MISO模拟混凝土受力时的粘塑性状态，模拟的混凝土本构关系图如图1所示。

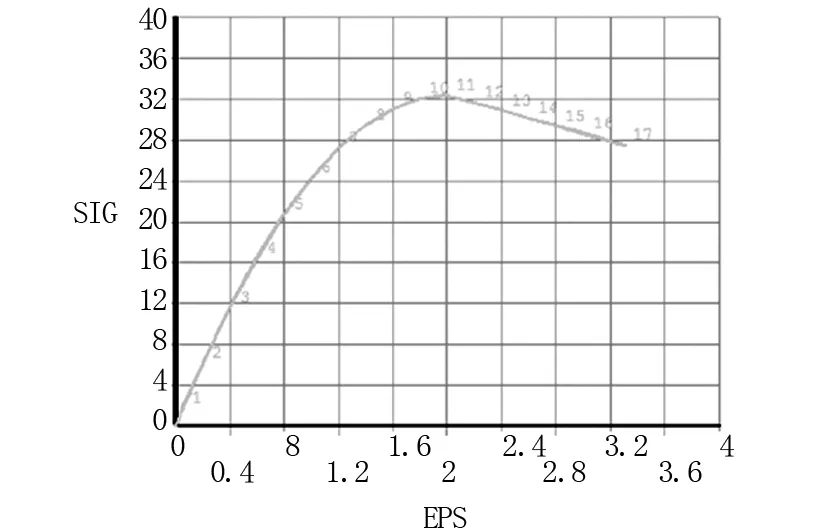
图1 本次建模的混凝土本构关系图

(2)钢筋本构关系

对于钢筋本构模型，采用双向性随动强化BKIN进行模拟，图2所示为钢筋应变曲线图。

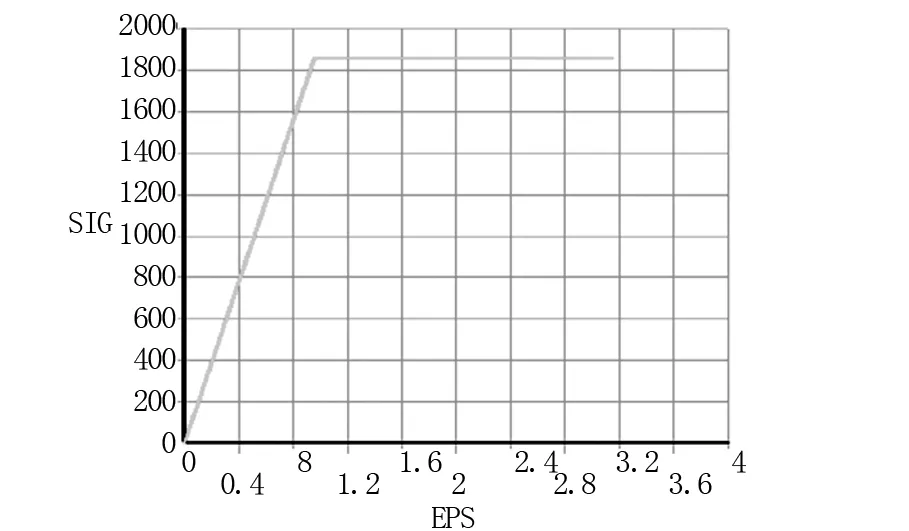
图2 钢筋的应变曲线关系图

1.4 裂缝模型建立

目前常见的裂缝处理方式主要是分离裂缝模型和分布裂缝模型。前者将裂缝处理为单元边界，当混凝土出现裂缝时，需要重新划分单元；后者基于混凝土的本构模型，认为材料具有各向异性，当混凝土出现裂缝时，只需要进行相应单元的调整就可以反馈梁体的裂缝情况，与实际更贴近且计算便捷[3]。因此本文预应力混凝土T梁的裂缝模型选择分布式裂缝。

2 模拟分析

2.1 施加外荷载

本次梁体裂缝模拟的加载采取分级加载的形式，每级为50 kN，直至模拟梁体出现裂缝。图3为预应力混凝土T梁在预应力筋及自重下产生的挠度模拟图，图4所示为其跨中横断面应力分布情况。

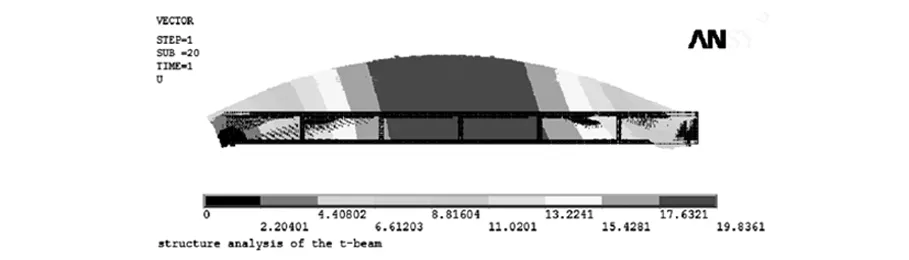
图3 梁上拱矢量图

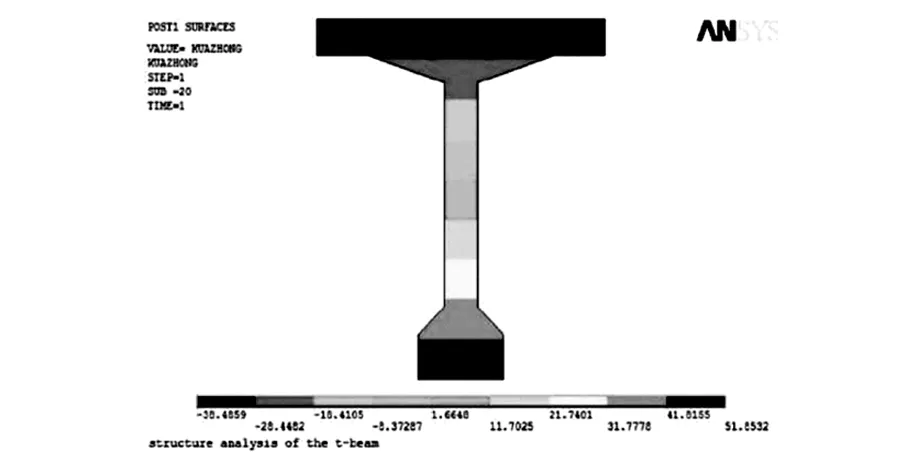
图4 跨中横截面应力分布图

2.2 挠度模拟计算结果

根据模型计算的预应力混凝土T梁的跨中挠度及荷载情况如表1及图5所示。

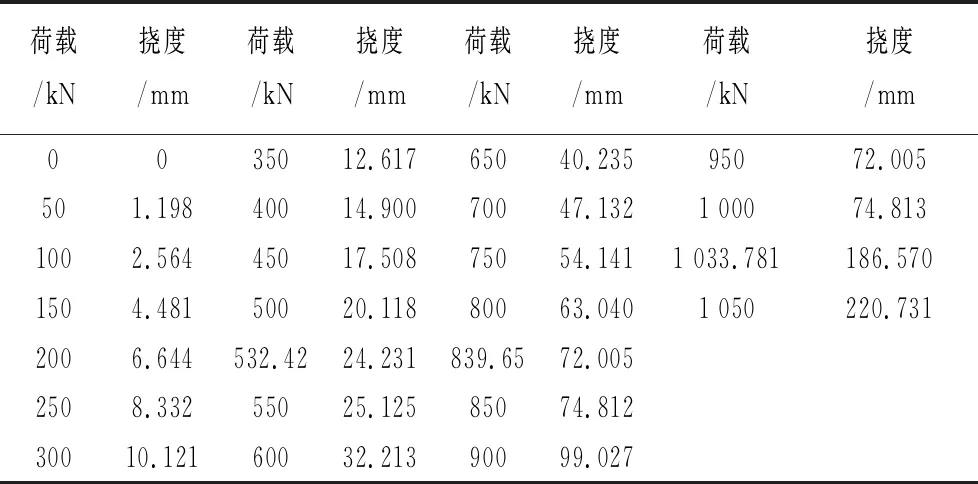
表1 预应力混凝土T梁模型跨中荷载及挠度情况

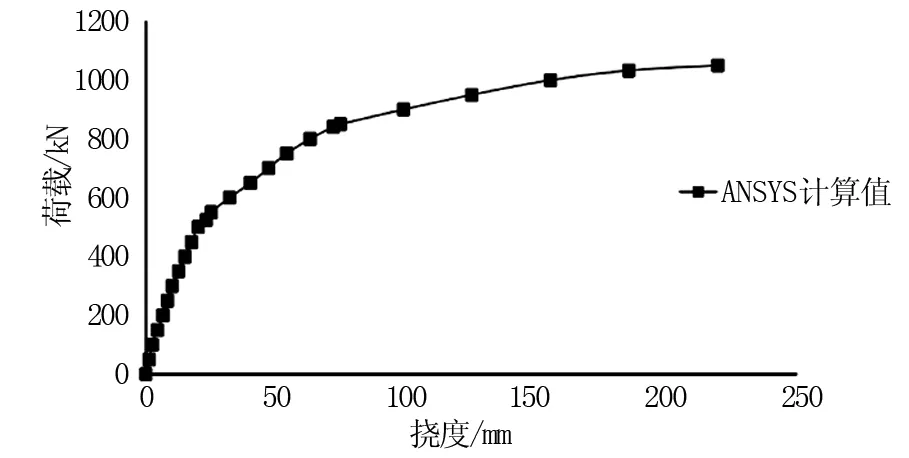
图5 模型T梁荷载与挠度曲线

由表1及图5不难看出，该预应力混凝土T梁模型的挠度变化分为三个阶段。第一阶段为弹性阶段，荷载与挠度关系呈现出明显的线性，模型梁在此阶段没有发生裂缝，刚度不变；第二阶段为弹塑性阶段，此阶段内混凝土开始出现裂缝，中性轴随着裂缝的发展而上升，模型梁的刚度也随之退化；第三阶段为塑性阶段，此时梁内钢筋出现屈服，随着荷载的增加，模型梁的刚度下降明显，挠度呈现较大幅度的增加[3]。

2.3 应变计算结果

表2所示为模型梁跨中梁顶的应变值随外荷载增长的变化情况。

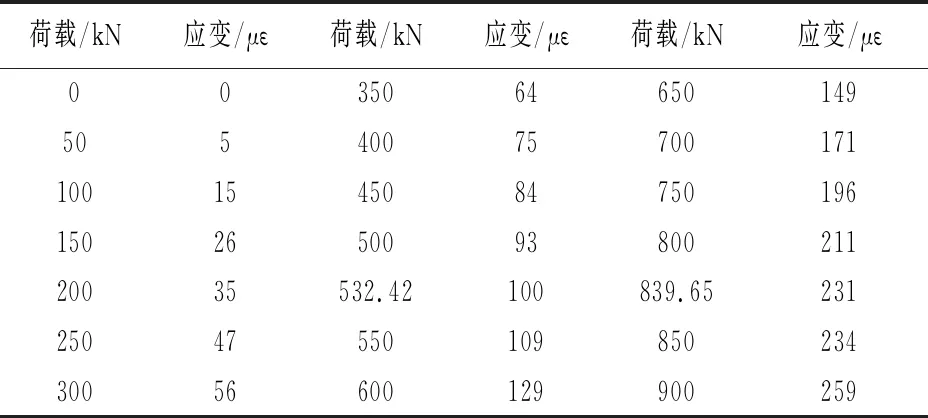
表2预应力混凝土T梁模型跨中荷载及应变情况

根据表2与图6可知，当模型梁出现裂缝时，荷载-应变曲线出现第一个拐点，模型梁的强度开始下降，应变出现突变。随着外荷载增大，模型梁处于弹塑性状态，应变仍随着荷载增大而增大，且增速上升、曲线斜率增大。随着荷载达到极限荷载，模型梁刚度下降，发生破坏。根据荷载与挠度、应变的关系，可以计算预应力混凝土T梁模型的开裂-屈服-破坏荷载，如表3所示。

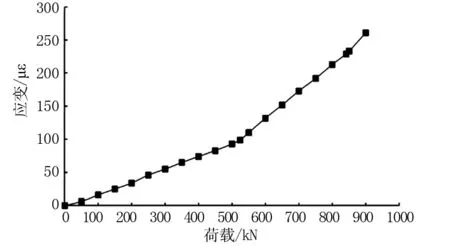
图6 跨中梁顶荷载与应变情况

表3 预应力混凝土T梁模型的荷载及挠度

2.4 裂缝结果

根据模型模拟情况，在荷载达到532.42 kN时，模型梁出现裂缝，裂缝最开始出现在跨中梁底处，沿垂直于轴线的方向对称发展；随着荷载的增大，裂缝进一步发育，沿垂直于轴线方向继续向上延伸，同时新的裂缝开始在两侧出现。荷载继续增加，梁底裂缝贯穿梁体，受拉区混凝土不再承受拉力，梁体的中轴线随着预应力筋开始受拉而逐渐上移。当荷载达到预应力筋屈服荷载时，裂缝迅速发展至贯穿梁体，受压混凝土被压碎。

3 数据比较分析

3.1 试验情况

为了验证模型建立与计算的准确性、有效性，项目制作了与中跨中梁同比例的试件进行静载试验。预应力混凝土T梁试件长30 m，跨径28.8 m，混凝土强度为C50，采用后张法布置预应力筋，保证两端张拉的对称均匀。本次静载试验通过检测仪器，观测试件随荷载增大时应变、位移、裂缝等参数的变化情况。

3.2 测试结果

在不考虑张拉引起的反拱度的情况下，循环加载试验所得的荷载-挠度观测结果如图7～图9所示。

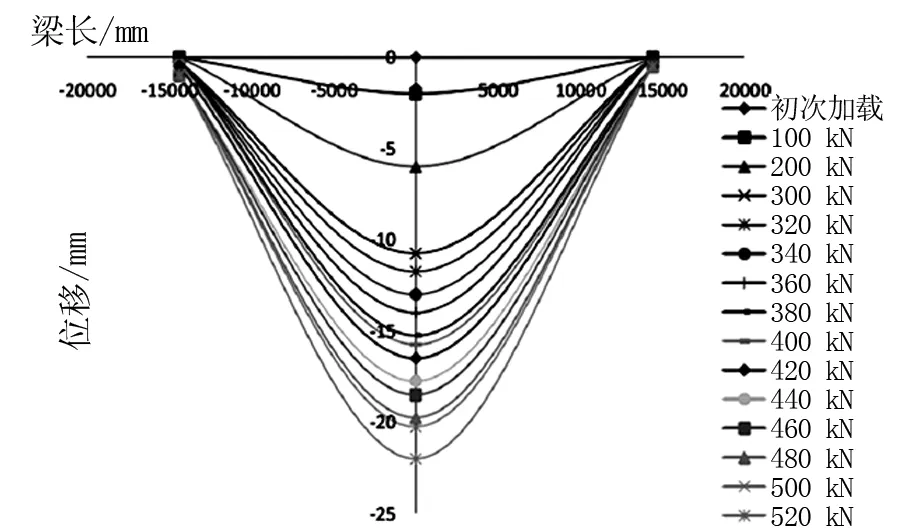
图7 第一次加载荷载-挠度关系

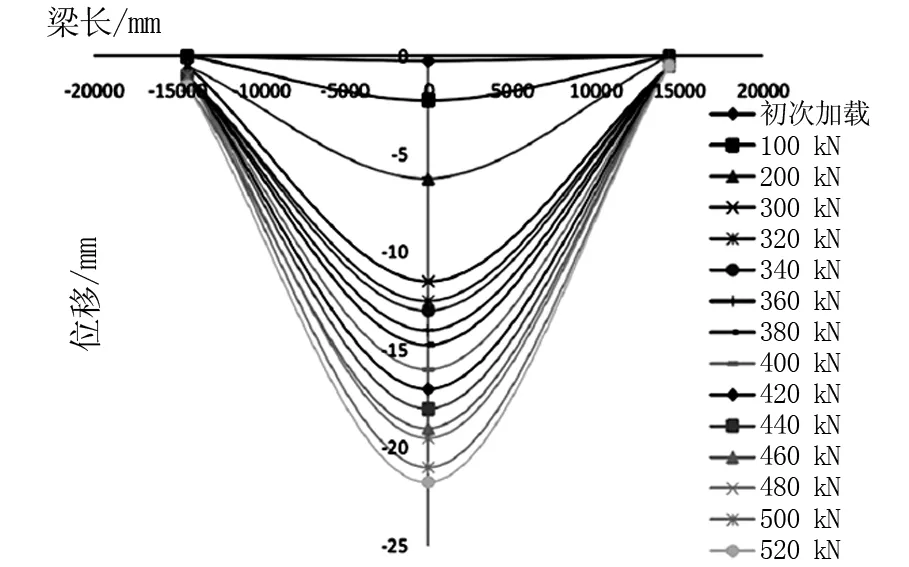
图8 第二次加载荷载-挠度关系

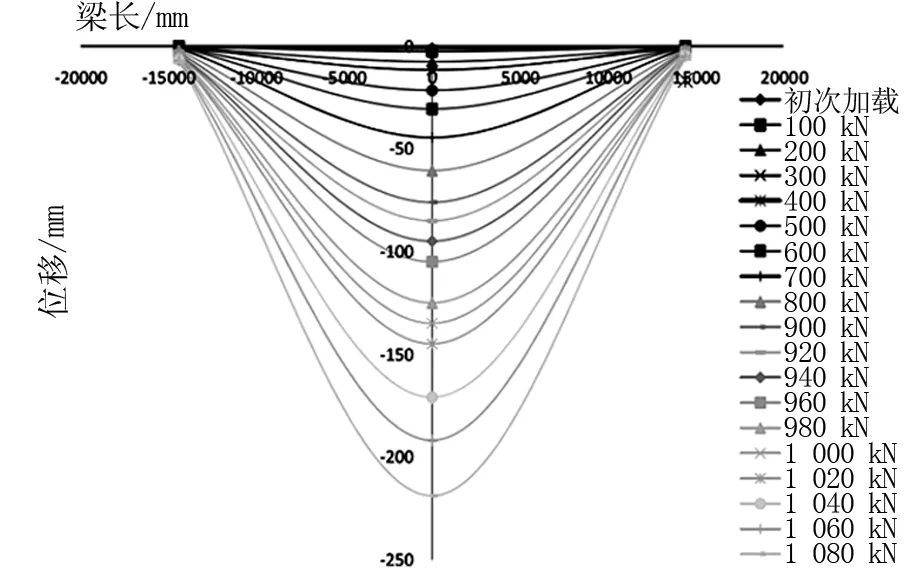
图9 第三次加载荷载-挠度关系

进一步考虑试件梁的挠度受支座沉降影响，对挠度曲线进行修正，最终得到荷载-挠度关系如图10所示。可以看出，三次循环开裂前曲线基本一致，表明在弹性阶段，预应力混凝土T梁的弹性能够恢复。第三次加载荷载时，曲线出现了较为明显的拐点。第一个拐点位于荷载522.41 kN处，此时试件底部混凝土受拉开裂，刚度突然降低；随着外部荷载增大，第二个拐点位于钢筋屈服荷载891 kN处，试件梁的刚度进一步降低；当跨中顶部达到破坏荷载1 075 kN时，受压区混凝土被压碎，梁体已经发生破坏。

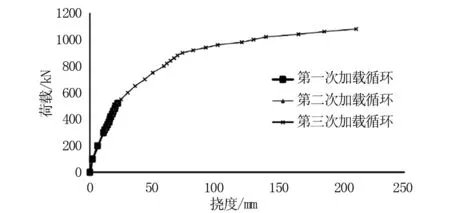
图10 荷载-挠度曲线修正图

3.3 模拟结果与试验结果的对比

将试验测得的荷载-挠度关系与模型模拟计算的结果进行对比，得到表4。

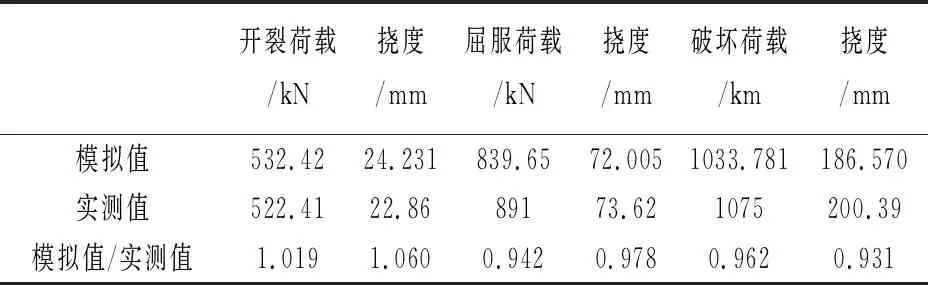
表4 试验与模拟的荷载与挠度数据比较

由表4可知，开裂荷载的模拟值较实测值略大，屈服荷载、破坏荷载的模拟值比实测值偏小，但相差的幅度均较小。分析原因可能在于模型建模时的材料参数与实际值虽然都满足规范范围，但是仍存在一定的差异，同时在建模时也对模型梁的复杂受力情况作了简化处理。但是整体来看，模型模拟与试件实测的荷载-挠度关系的吻合程度较好，说明建立的预应力混凝土T梁裂缝模型，能够较为准确、有效地模拟梁体的实际工作状态，值得推广应用。