微元法在高中物理教学中的应用

裴加旺 刘 蕊

(北京景山学校,北京 100006)

1 引言

微元法是分析、解决物理问题的常用方法,体现了从部分到整体的科学思维。使用微元法处理问题时,需将研究对象或研究的过程在空间或时间上进行无限细分,得到无数个“微元”或“元过程”,它们所遵循的物理规律是相同的。我们用已知的可求的规律分析单个“微元”或“元过程”,再将分析结果应用适当的物理思想或数学方法进行处理,获得关于研究对象或过程整体的规律。

本文中我们主要分析两类应用微元法求解的问题,一类是分析变量变化率的问题,另一类是求变化量的累积效果问题。从数学角度看,前一类问题对应着微分思想,后一类问题对应着积分思想,解决它们的关键都在于对微元的选取和处理,一是要正确地应用物理规律写出微元相关表达式,二是要对微元表达式进行合适的处理。

2 微元法在高中物理应用的实例分析

2.1 利用微元分析变量的变化率

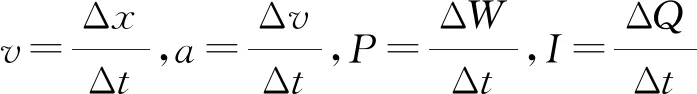
例1：一物体做变速直线运动,推导速度对时间的变化率与速度对空间的变化率的关系,并应用该结论证明在自由落体运动过程中速度对空间变化率在逐渐减小。

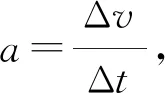
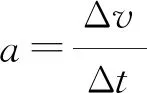
例2：物体沿着圆周的运动是常见运动,匀速圆周运动是其中最简单的一种,匀速圆周运动是一种变速运动,具有加速度。

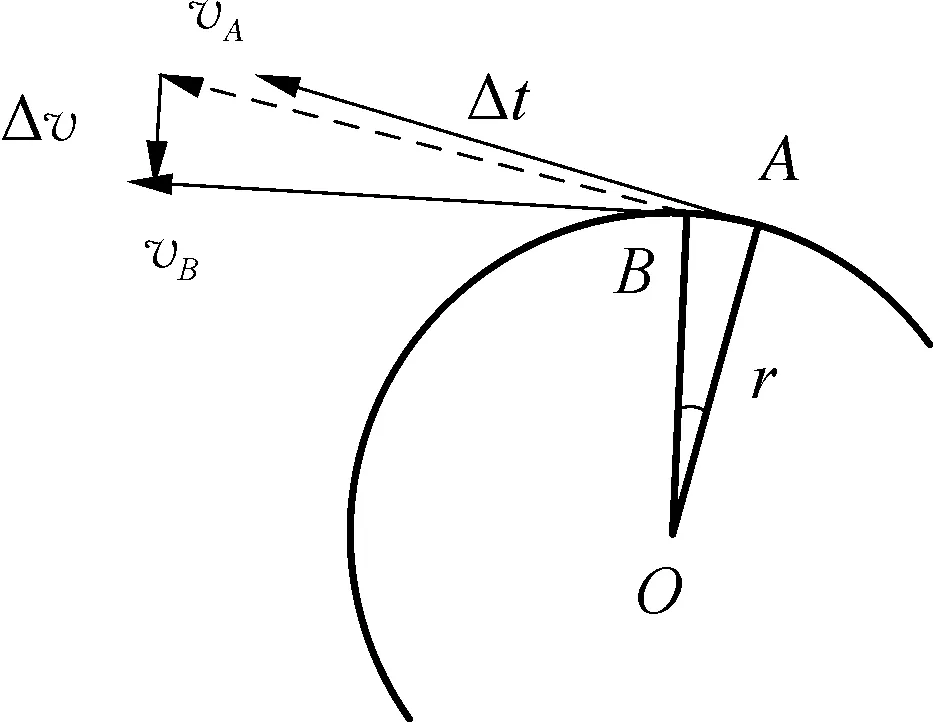
(1) 可按如下模型来研究做匀速圆周运动的物体的加速度，设质点沿圆心为O、半径为r的圆周运动,速度大小恒定为v,某时刻质点运动到位置A,经极短时间Δt后到达位置B,如图1甲所示,请根据加速度的定义,推导该质点运动到位置A时加速度的大小aA。

(2) 研究匀变速直线运动的“位移”时,常应用“以恒代变”的方法，研究曲线运动的“瞬时速度”时,常用“化曲为直”的方法。而在研究一般曲线运动时,用的更多的是 “化曲为圆”的方法,即对于一般曲线运动,尽管曲线上各位置的弯曲程度不同,但可以在研究时将曲线分割为许多很短的小段,质点在每一小段的运动均可看作半径为某个半径为ρ的圆周运动的一部分,可以采用分析圆周运动的方法进行研究,ρ称为曲线的曲率半径,如图1乙所示,请据此分析图1丙所示的斜抛轨迹在最高点处的曲率半径ρ。

甲

(3) 事实上,对于涉及曲线运动加速度问题的研究中,“化曲为圆”并不是唯一的方法,我们还可以采用一种“化圆为抛物线”的思考方式,匀速圆周运动在短时间Δt内可以分解为沿切线方向的匀速运动、沿法线方向的匀变速运动。设圆弧半径为R,质点做匀速圆周运动的速度大小为v,请推导质点做匀速圆周运动过程中的向心加速度a。

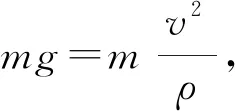
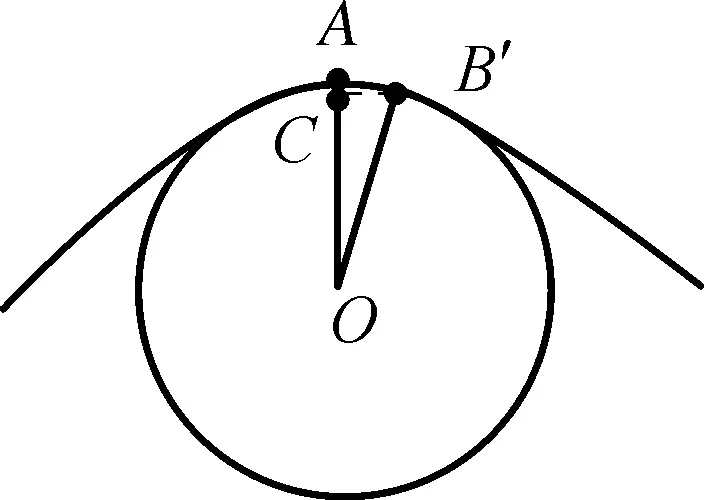
图2

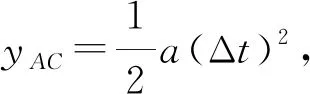
点评:解决实际问题时我们希望了解瞬时变化率的特征。这时就需要先用微元的形式把一段时间或一段空间的平均变化率表示出来,得到的表达式体现了物理规律在“元过程”的应用(上面两道例题里应用到了运动学定律和牛顿第二定律)。在取极值求瞬时变化率的时候,要注意当时间或空间变量趋近于零时,描述微元的方式同描述整体量的方式相比可能发生了变化,在极限情况下对表达式进行一些合理的数学近似和处理,就是所谓的“化变为恒”“化曲为直”“化曲为圆”“化圆为抛物线”的思想,把难以解决的问题转化为容易解决的问题。

2.2 利用微元求和，求变化量的累积效果

在物理研究中,经常会遇到变化量的累积效果问题。在高中阶段的学习中就遇到很多这类问题,比如变速运动位移问题、变力做功问题、变力冲量问题和电容器储存电荷量问题等。在人教版教材中,探究匀变速运动的位移公式、探究弹簧弹性势能的表达式、观察电容器充放电过程等内容都用到了微元法。微元法在处理变化量的累积效果问题时,通过限制变化发生的空间和时间来限制变化,化“全过程中的变量”为“元过程中的恒量”,进而可以用适用于恒量的公式去描述和分析“元过程”,实现“化变为恒”“化曲为直”。进一步对变量在“元过程”中的效果进行累积求和,就可以得到变化量在全过程的累积效果。

应用微元法处理该类问题,一般分为两步:

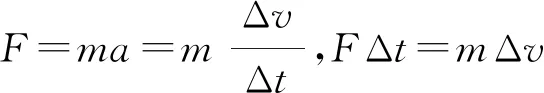
(2) 通过数学处理,对“元过程”的效果累积求和得到可解方程,再对未知量进行求解。这一步经常用到的方法是图像法，把相关函数图像与坐标轴所围的“面积”作为求和运算的结果。人教版教材中探究匀变速运动的位移公式、探究弹簧弹性势能的表达式、观察电容器充放电过程等内容中,都用到了这种处理方法。在解题时,当题目给出了某种变量y随另一变量x改变的y-x图像时,就可尝试使微元表达式中含有yΔx的形式,进而用图像法求解。

图3

例3：如图3所示,两根光滑的平行金属导轨水平放置且与电阻为R的导体相连,导轨之间距离为L,其所在空间存在垂直于导轨平面的匀强磁场,磁感应强度为B。有一导体棒ab,质量为m,在导轨上以初速度v0向右运动,导轨和棒的电阻均不计。求:

(1) 在导体棒的整个运动过程中通过闭合回路的电荷量q；

(2) 导体棒在整个运动过程中的位移x。

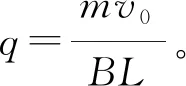
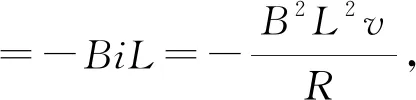
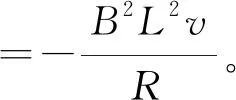
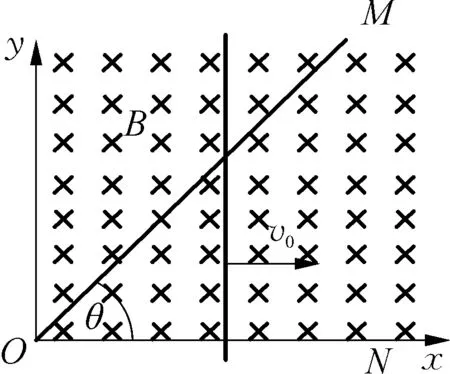
图4

例4：如图4所示,金属导轨MON固定在水平平面内,其顶角θ=45°,其处在竖直方向的磁感应强度为B的匀强磁场中。一根垂直于ON的导体棒在水平外力作用下沿导轨MON以恒定速度v0向右滑动,导体棒质量为m,棒与导轨单位长度的电阻均匀为r。在滑动过程中棒与导轨始终保持良好接触。t=0时,导体棒位于O处,求:若在t0时刻撤去外力F,导体棒最终静止在导轨上的坐标x。

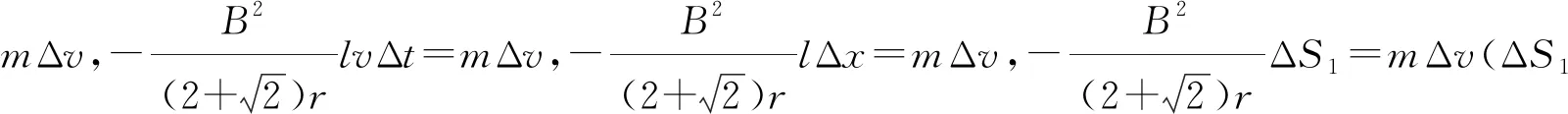
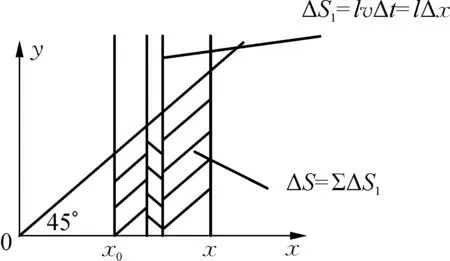
图5

点评:在本题中进行了换元计算，lvΔt=lΔx=ΔS1,把时间元先换成了线段元,再换成了面积元,这样做可以用导体棒扫过的面积代表微元累积之和。用微元法解题时，原始公式中的微元在解题过程中可能根据需要替换成其它微元,替换的目标是新微元累积求和的结果可以用题目已知条件表示出来。

3 应用微元法解题的策略

应用微元法解题可以分为3个步骤:微元的选取、微元过程的物理表达和对微元表达式的处理。

(1) 要根据题目的情景选取合适的微元,如Δt、Δx、ΔS面、ΔV体、Δm、Δq等,要确保选取的微元能够对应一定的元过程,该元过程具有整个过程所不具备的“优越性”,体现在“化变为恒”“化曲为直”上,使得不能在全过程中应用的公式可以应用在元过程中,并且每一个元过程都遵循同样的规律。

(2) 把物理规律用微元表达式体现出来,这里表达式的选取要有目的性,要能够把已知量和待求量联系起来,还要有利于进一步的数学处理。

(3) 利用换元法、图像法等方法对微元表达式进行求和处理,得到结果。

微元法的应用要建立在学生深刻理解物理规律、物理量之间的内在联系的基础上。教师进行微元法的教学时,要通过对经典例题的讲解,引导学生反思总结,提高学生对知识的关联整合能力,提高学生对问题本质的分析概括能力,进而能够在不同情境中实现知识和方法的迁移,切实提升学生的物理学科核心素养。