高速公路经营者与使用者行为策略的演化博弈分析
2022-04-15刘拥华姚逸豪李洁云段莉珍
刘拥华,姚逸豪,李洁云,申 科,段莉珍,
(1.昆明理工大学 交通工程学院, 昆明 650500;2.云南省交通科学研究院有限公司, 昆明 650011)
当前,我国高速公路建设里程已跃居世界第一,公路路网的通行效率极大提高,满足了各行业的物流需求[1-2]。然而,在高速公路局部路段通行能力尚有富余的情况下,部分道路网的平行老路存在交通拥堵情况,不仅造成了交通基础设施资源的浪费,也给平行老路增加了通行压力。究其原因,主要是交通部门对高速公路差异化收费政策的推行力度尚有不足,客货车司机选择不同的出行路线能获得的效益差不明显。同时,在差异化收费政策下,选择高速公路出行花费的通行费额和能获得的效益也是影响高速公路局部路段车流量的重要因素。因此,如何利用经济杠杆调节平行老路的流量,将其分流到高速公路,协调好高速公路经营者与使用者双方的利益,是高速公路管理决策中亟待解决的关键问题。
近年来,交通运输部出台了多项政策,探索高速公路差异化收费。国内学者也对高速公路差异化收费措施进行了深入研究。李昊等[3]将车辆排放水平作为费率的影响因素进行高速公路差异化费率分析。刘伟铭等[4]利用双层规划理论求解各收费路段的最优费率与相应的路网交通流量。闫丹丹等[5]以经济学原理为基础,建立基本费率与从量费率的模型,并采用两部制对高速公路进行收费定价。上述研究都对高速公路差异化收费措施进行了分析,以制定合理的收费费率为主,但未对差异化收费措施实行后高速公路经营者与使用者双方的行为策略做进一步研究,缺少行为策略的仿真模拟分析。另一方面,学者们对高速公路差异化费率的研究表明,博弈论能有效刻画差异化收费措施实行过程中高速公路经营者与使用者之间的行为策略演化。梁秀峰等[6]将演化博弈模型应用于PPP项目绩效支付机制研究。刘长玉等[7]将演化博弈模型用于分析政府监管政策对制造商生产策略的选择影响。现有的演化博弈方法被应用于策略选择,但博弈过程中涉及参数还需要更细致的定性分类,博弈双方的初始策略选择概率也需要多层次的考虑,所涉及的影响因子对演化趋势和演化速率的影响仍有待深入探究。
高速公路差异化收费研究多从经营者一方考虑高速公路定价模型,较少从高速公路利益相关者组成系统的角度进行整体研究。高速公路经营者与使用者的行为具备不完全理性的特征,且随着时间的推移,双方会在各自的策略集中不断做出调整[8]。本文研究基于博弈论做出若干合理假设,构建高速公路经营者与使用者的演化博弈模型,进一步考虑初始策略选择概率不同的情况,研究系统博弈均衡点的稳定性,分析系统内双方主体的演化趋势,并剖析博弈策略中影响因子不同取值时对高速公路利益相关者系统演化结果的影响,探索博弈系统的内部演化机理,从而最大限度地发挥高速公路的网络效益,实现道路资源均衡利用的目标。
1 高速公路利益相关者演化博弈模型
1.1 博弈模型假设与博弈收益分析
采用演化博弈来构建高速公路经营者与使用者行为策略的模型。系统中的主要利益相关者为高速公路经营者与使用者。受信息不对称和环境因素的影响,两者都具备有限理性的特性,且双方处于信息不完全对称状态[9-10]。通过动态演化分析结果,提出利用价格杠杆来引导平行老路的车流量分配到高速公路的措施,引导车辆出行,实现公路资源的均衡利用,缓解城市交通拥堵。构建的演化博弈模型中,高速公路经营者的策略集为:{做出差异化收费调整措施,不做出差异化收费调整措施},高速公路使用者的策略集为:{高速公路出行,平行老路出行}。针对该模型有以下假设:
假设1高速公路经营者群体中选择“做出差异化收费调整措施”的群体选择概率为x(0≤x≤1),选择“不做出差异化收费调整措施”的群体选择概率为1-x;高速公路使用者群体中选择“高速公路出行”的群体选择概率为y(0≤y≤1),选择“平行老路出行”的群体选择概率为1-y。
假设2高速公路费率的制定需经过一系列严谨的经营成本测算程序。与传统的高速公路费率定价不同的是,除了高速公路投资规模、通行量及通行营业成本的测算,差异化费率的制定还需要同时考虑平行老路的通行量,调查客货车司机选择不同路线的原因,并对征收费用、经营服务费用及通行养护委托服务费用等进行统计分析,产生额外的人力和物力成本。将车流量合理地吸引到高速公路,对货物运输、招商引资等均能起到较好的效果,提高社会效益。假设高速公路经营者选择“做出差异化收费调整措施”时的成本为N1,能带来的社会效益为G1;选择“不做出差异化收费调整措施”时的成本为N2,能带来的社会效益为G2。
假设3高速公路使用者的出行成本一般从使用者成本、时间成本和外部成本3个方面进行定量分析。使用者成本指财务方面的成本,例如通行费、油费与交通工具折旧费等;时间成本指乘车时间,以居民工资平均定价来量化;外部成本包括环境污染、拥挤程度与交通事故3个方面,其中拥挤成本一般考虑由于路段饱和度增大、车辆运行速度差较大导致的驾驶舒适度降低情况。假设高速公路使用者选择“平行老路出行”时的成本为C,能获得的时间效益为R;选择“高速公路出行”时付出的额外成本为ΔC,能获得的额外时间效益为ΔR。
假设4高速公路使用者采用不同的路线出行时,受到出行时段和不可抗力(比如交通事故、临时交通管制等)的影响,导致无论高速公路使用者选择哪种出行路线都存在一定概率的拥堵问题。若区域内做出差异化收费调整措施,则:高速公路使用者选择“高速公路出行”时遇上拥堵的概率为α1,选择“平行老路出行”时遇上拥堵的概率为β1;若区域内不做出差异化收费调整措施,则:高速公路使用者选择“高速公路出行”时遇上拥堵的概率为α2,选择“平行老路出行”时遇上拥堵的概率为β2。但由于平行老路的道路宽度不足,交通管理水平较低,机动车出行时易受其他类型车辆与行人的严重干扰,所以选择“平行老路出行”时遇上拥堵的概率β1、β2大于选择“高速公路出行”时遇上拥堵的概率α1、α2。
假设5道路拥堵会同时对高速公路经营者和使用者的效益产生影响。对高速公路使用者一方来说,若选择“高速公路出行”,遇上拥堵时的时间效益损失量为E1,选择“平行老路出行”,遇上拥堵时的时间效益损失量为E2;对高速公路经营者一方来说,高速公路拥堵时的社会效益损失量为E。社会效益损失量主要包含3个方面:一是沿线诸项功能的衰退,严重时将引发环境恶化;二是抑制人们的日常活动,使城市活力大幅度降低,生活质量也随之下降;三是增加了交通事故的发生率,造成各种直接或间接损失。
假设6当高速公路经营者选择“做出差异化收费调整措施”且运用高水平的交通管理措施使高速公路有序通行时,高速公路经营者能获取来自高速公路上级集团公司的直接经济奖励和来自社会公众的额外声誉奖励,合计为W(W>N1>0)。
根据上述假设,构建高速公路经营者与使用者博弈支付矩阵,如表1所示。
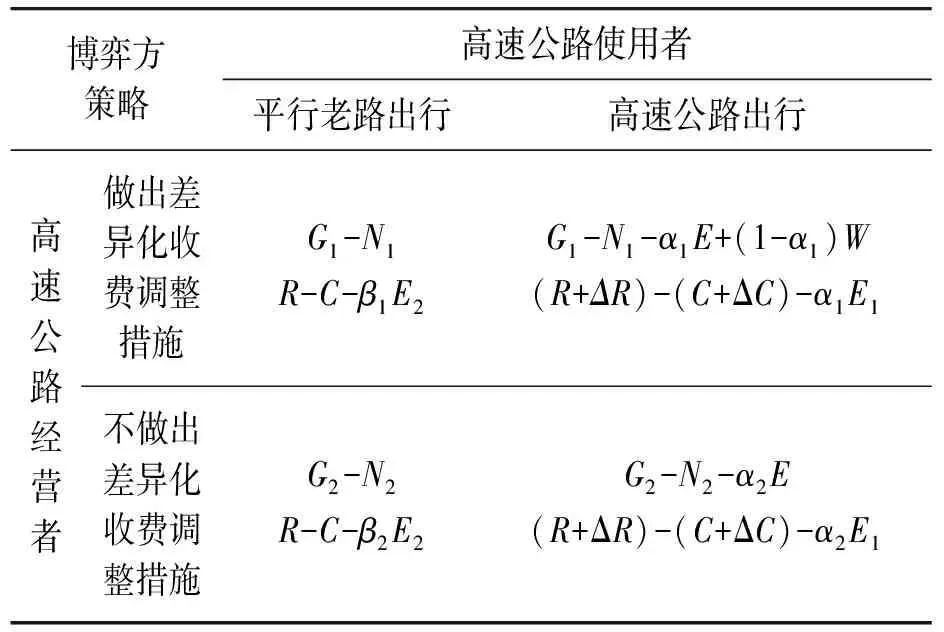
表1 高速公路经营者与使用者博弈支付矩阵
1.2 复制动态方程构造
根据表1中的博弈支付矩阵,计算得到高速公路使用者选择“平行老路出行”时的期望收益EP1和选择“高速公路出行”时的期望收益EP2,分别为:
EP1=x(R-C-β1E2)+
(1-x)(R-C-β2E2)=
R-C-β2E2-xβ1E2+xβ2E2
(1)
EP2=x[(R+ΔR)-(C+ΔC)-α1E1]+
(1-x)[(R+ΔR)-(C+ΔC)-
α2E1]=R+ΔR-C-ΔC-
α2E1-xα1E1+xα2E1
(2)
根据Malthusian动态方程,构建高速公路使用者方的复制动态方程F(y)为:
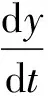
y(1-y)[ΔC-ΔR-β2E2+α2E1+
x(β2E2-β1E2+α1E1-α2E1)
(3)
同理,计算得到高速公路经营者选择“做出差异化收费调整措施”时的期望收益Eq1和选择“不做出差异化收费调整措施”时的期望收益Eq2,分别为:
Eq1=y[G1-N1-α1E+(1-α1)W]+
(1-y)(G1-N1)=
G1-N1+yW-yα1E-yα1W
(4)
Eq2=y(G2-N2-α2E)+
(1-y)(G2-N2)=
G2-N2-yα2E
(5)
根据Malthusian动态方程,构建高速公路经营者方的复制动态方程F(x)为:
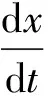
x(1-x)(Eq1-Eq2)=
x(1-x)[G1-G2+N2-N1+
y(W-α1E-α1W+α2E)
(6)
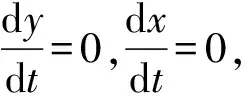
(7)
(8)
1.3 演化博弈均衡点稳定性分析
复制动态方程所确定的演化博弈均衡点并非都是均衡稳定策略(equilibrium stabilization strategy,ESS)[12-13]。根据Friedman理论,高速公路利益相关者系统的渐近稳定性可借助系统雅可比(Jacobian)矩阵局部稳定性进行分析[14-16]。系统的雅可比矩阵J为:
(9)
a11=(1-2x)[G1-G2+N2-N1+
y(W-α1E-α1W+α2E)]
(10)
a12=x(1-x)(W-α1E-α1W+α2E)
(11)
a21=y(1-y)(β2E2-β1E2+α1E1-α2E1)
(12)
a22=(1-2y)[ΔC-ΔR-β2E2+
α2E1+x(β2E2-β1E2+
α1E1-α2E1)]
(13)
(14)

(15)
情况1如表3所示,当满足条件G1-G2+N2-N1<0且ΔC-ΔR-β2E2+α2E1<0时,点(0,0)是局部稳定的ESS点。

表3 基于情况1的均衡稳定策略分析结果
情况2如表4所示,当满足条件G1-G2+N2-N1+W-α1E-α1W+α2E<0且-ΔC+ΔR+β2E2-α2E1<0时,点(0,1)是局部稳定的ESS点。
情况3如表5所示,当满足条件-G1+G2-N2+N1<0且ΔC-ΔR-β1E2+α1E1<0时,点(1,0)是局部稳定的ESS点。
情况4如表6所示,当满足条件-G1+G2-N2+N1-W+α1E+α1W-α2E<0且-ΔC+ΔR+β1E2-α1E1<0时,点(1,1)是局部稳定的ESS点。

表4 基于情况2的ESS分析结果

表5 基于情况3的ESS分析结果

表6 基于情况4的ESS分析结果
2 演化博弈动态仿真分析
2.1 均衡稳定策略的演化路径分析
为进一步探究高速公路使用者与经营者行为策略的动态演化过程和演化博弈机理,使用Matlab软件进行数值仿真,在限制条件下设定相关仿真参数,分析双方博弈过程中的策略选择及演化规律。
情况1当满足条件G1-G2+N2-N1<0且ΔC-ΔR-β2E2+α2E1<0时,高速公路经营者与使用者双方的演化博弈趋势如图1所示。随着时间的推移,高速公路经营者一方在博弈中选择“做出差异化收费调整措施”的群体选择概率x会趋向于0;而高速公路使用者一方选择“高速公路出行”的群体选择概率y也会趋向于0,最终系统的稳定状态点为(0,0)。即当满足上述条件时,双方的演化路径为选择“平行老路出行”和“不做出差异化收费调整措施”。
情况2当满足条件G1-G2+N2-N1+W-α1E-α1W+α2E<0且-ΔC+ΔR+β2E2-α2E1<0时,高速公路经营者与使用者双方的演化博弈趋势如图2所示。随着时间的推移,高速公路经营者一方在博弈中选择“做出差异化收费调整措施”的群体选择概率x会趋向于0;而高速公路使用者一方选择“高速公路出行”的群体选择概率y会趋向于1,最终系统的稳定状态点为(0,1)。即当满足上述条件时,双方的演化路径为选择“高速公路出行”和“不做出差异化收费调整措施”。
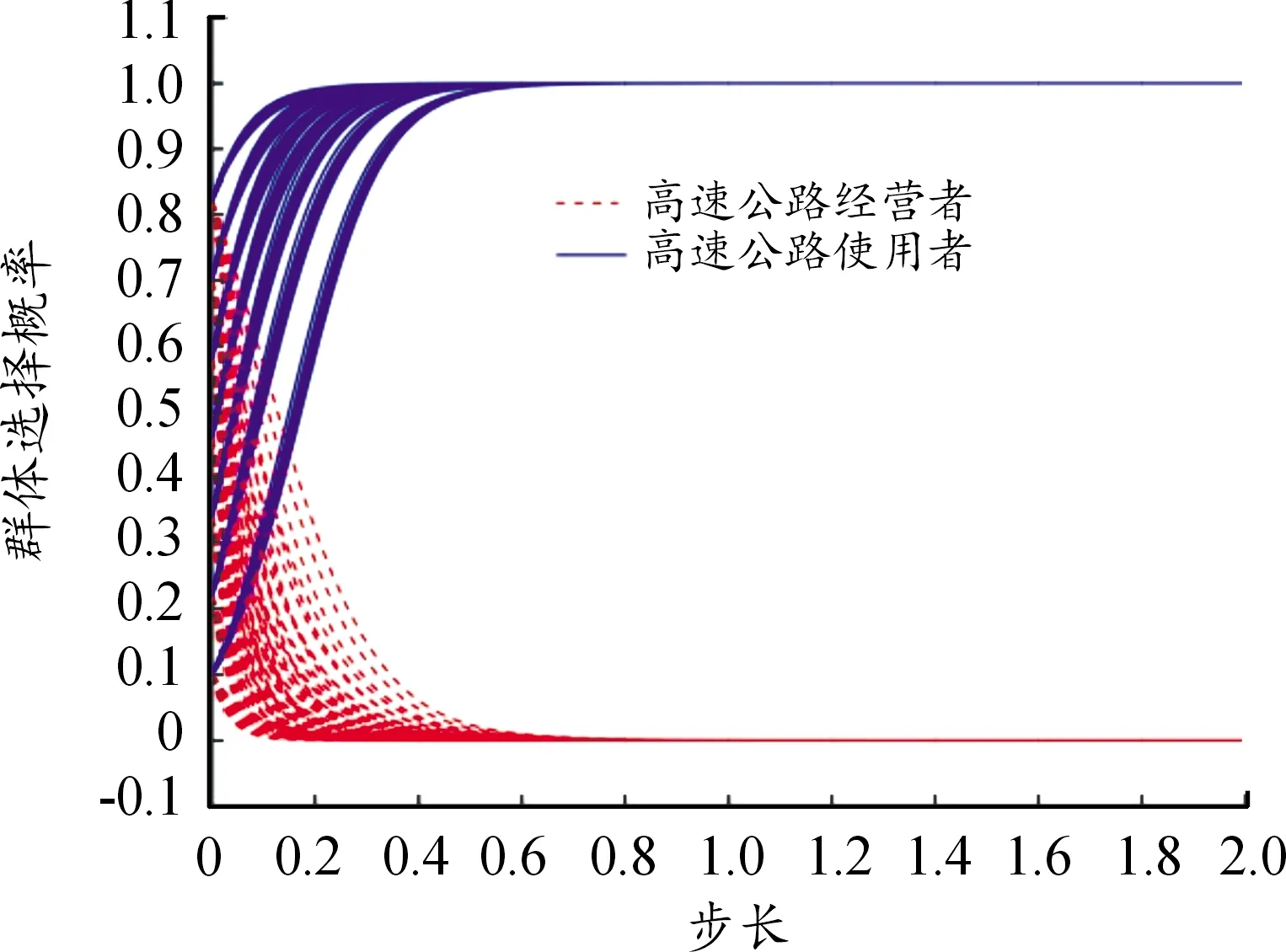
图2 稳定点(0,1)的仿真结果
情况3当满足条件-G1+G2-N2+N1<0且ΔC-ΔR-β1E2+α1E1<0时,高速公路经营者与使用者双方的演化博弈趋势如图3所示。随着时间的推移,高速公路经营者一方在博弈中选择“做出差异化收费调整措施”的群体选择概率x会趋向于1;而高速公路使用者一方选择“高速公路出行”的群体选择概率y会趋向于0,最终系统的稳定状态点为(1,0)。即当满足上述条件时,双方的演化路径为选择“平行老路出行”和“做出差异化收费调整措施”。
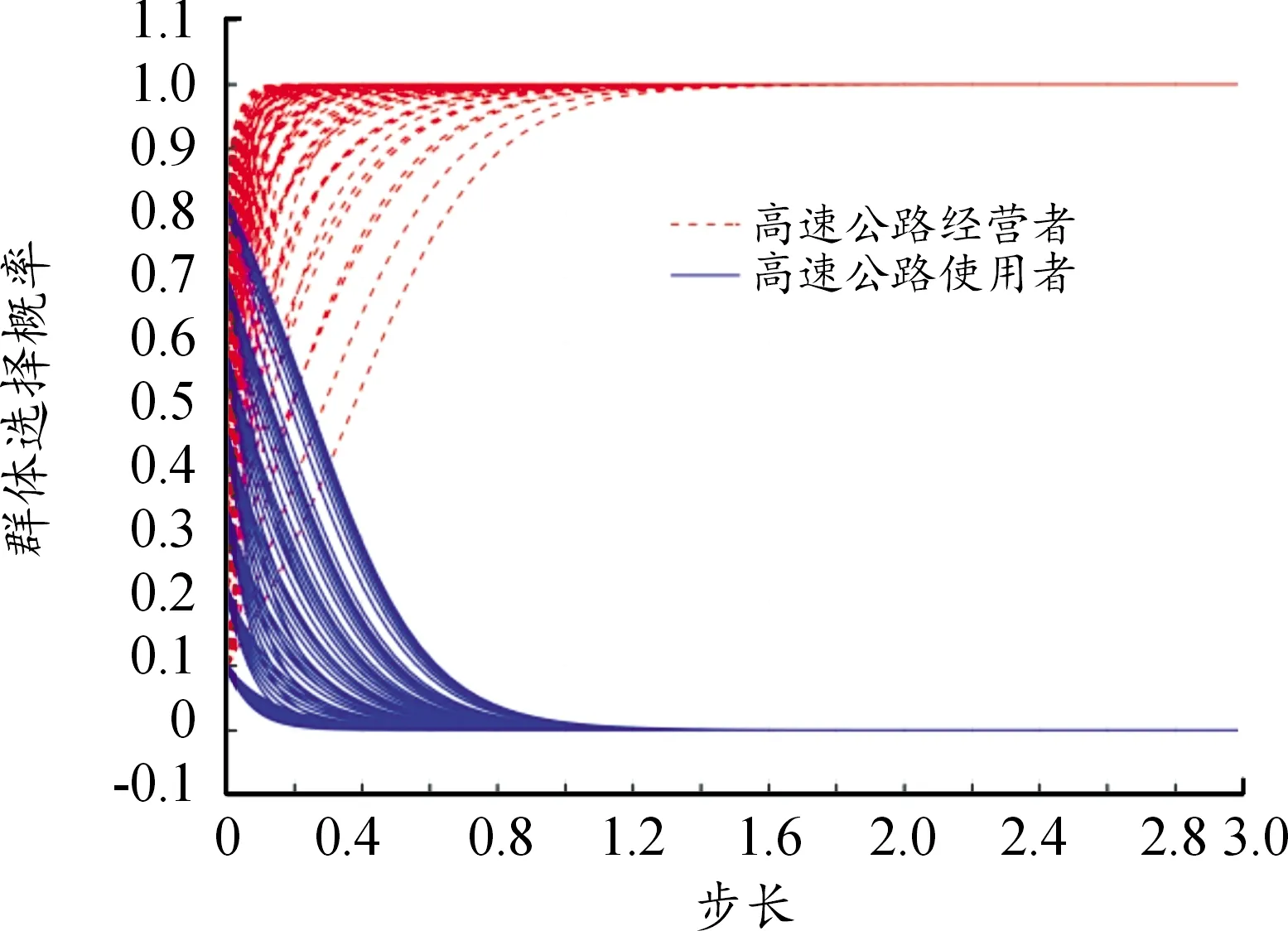
图3 稳定点(1,0)的仿真结果
情况4当满足条件-G1+G2-N2+N1-W+α1E+α1W-α2E<0且-ΔC+ΔR+β1E2-α1E1<0时,高速公路经营者与使用者双方的演化博弈趋势如图4所示。随着时间的推移,高速公路经营者一方在博弈中选择“做出差异化收费调整措施”的群体选择概率x会趋向于1;而高速公路使用者一方选择“高速公路出行”的群体选择概率y也会趋向于1,最终系统的稳定状态点为(1,1)。即当满足上述条件时,双方的演化路径为选择“高速公路出行”和“做出差异化收费调整措施”。
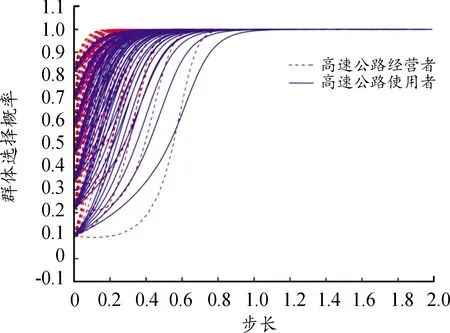
图4 稳定点(1,1)的仿真结果
2.2 博弈策略收敛速度分析
演化博弈中,若高速公路的交通管理水平不高、线形条件不佳、高速公路上级集团公司经济奖励力度不足时,双方向(1,1)收敛的速度也将不同。因此,接下来分析博弈策略中影响因子的不同取值对高速公路利益相关者系统演化结果的影响,探索博弈系统的内部演化机理。
2.2.1高速公路拥堵率对双方主体演化影响
以情况4参数取值为基础,对α1分别取值0.1、0.2、0.3,研究其对博弈系统内双方主体演化趋势的影响,如图5、6所示。
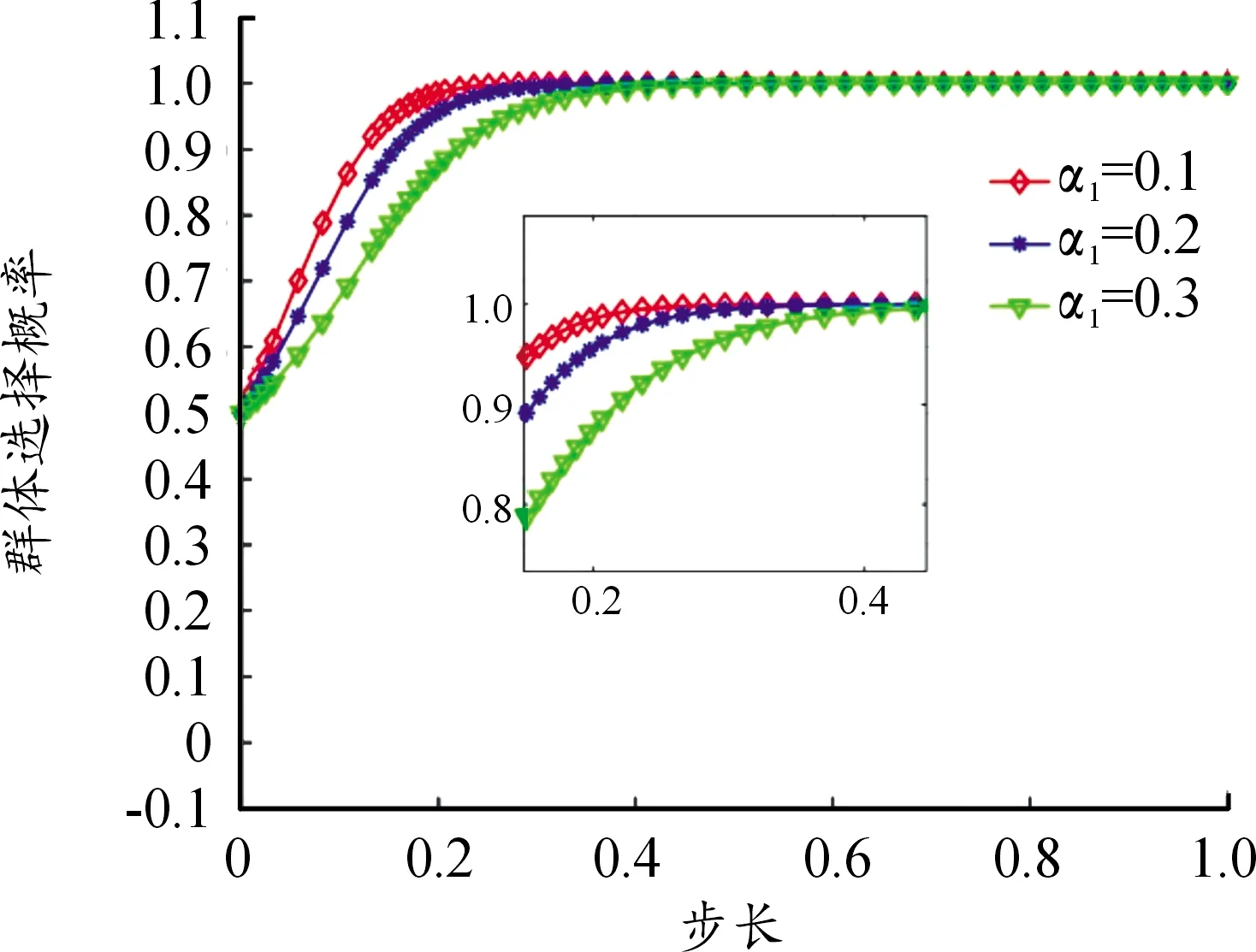
图5 α1变化对高速公路经营者方演化影响曲线
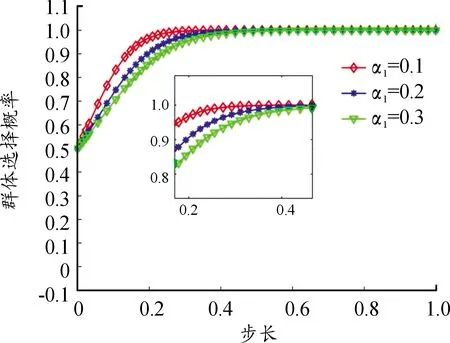
图6 α1变化对高速公路使用者方演化影响曲线
由图5、6可知,在情况4参数取值条件下,高速公路拥堵率的改变不影响高速公路利益相关者双方的选择概率演化趋势。双方的群体选择概率均趋向于1,拥堵率仅改变双方策略演化的速率;拥堵率越低,双方向(1,1)收敛的速度也越快,起明显的促进作用。
2.2.2上级集团公司经济奖励力度对双方主体演化影响
以情况4参数取值为基础,对W分别取值40、50、60,研究其对博弈系统内双方主体演化趋势的影响,如图7、8所示。
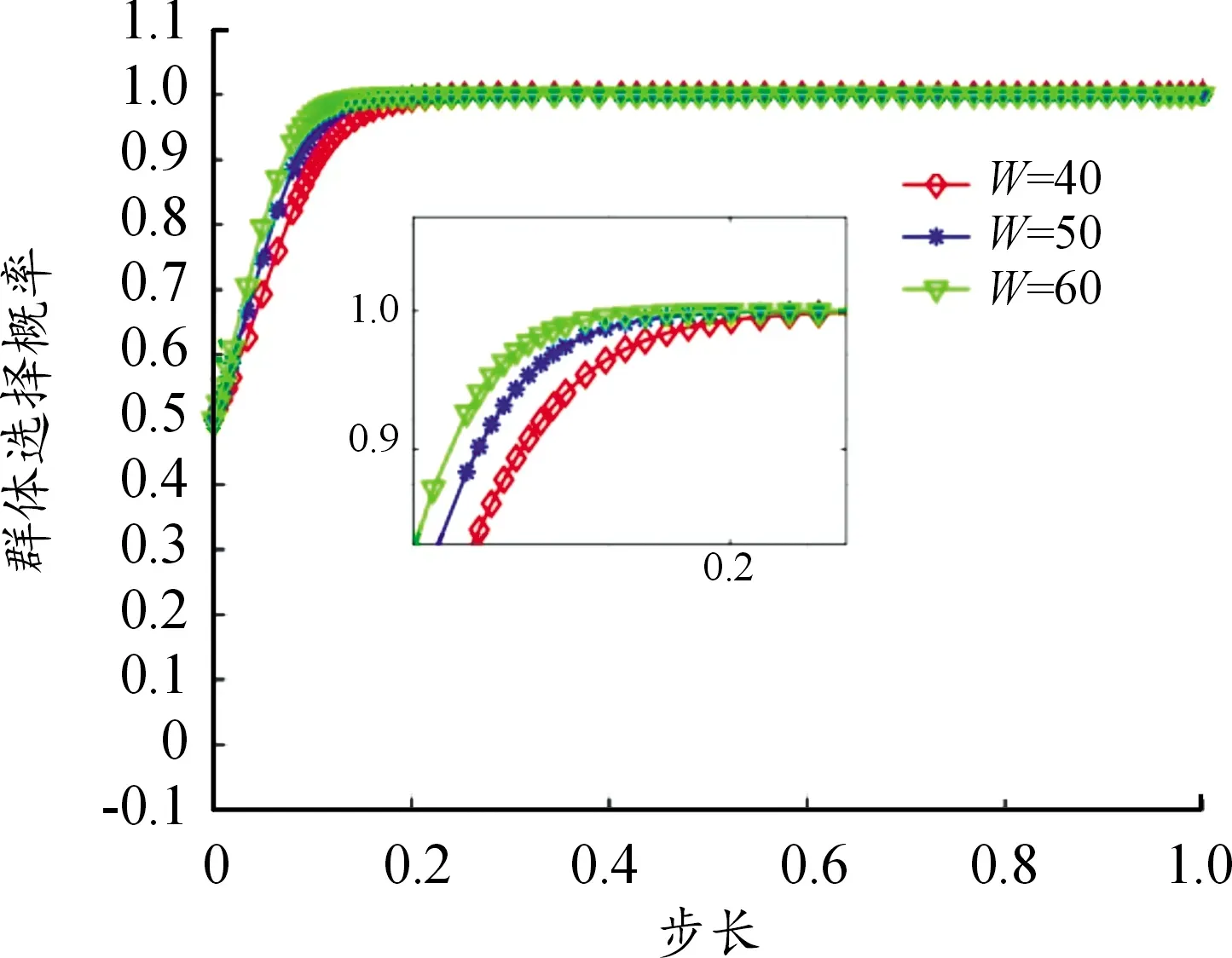
图7 W变化对高速公路经营者方演化影响曲线
由图7可知,在情况4参数取值条件下,上级集团公司经济奖励力度的改变不影响高速公路经营者的选择概率演化趋势,群体选择概率趋向于1;上级集团公司经济奖励力度仅改变策略演化的速率,经济奖励力度与高速公路经营者的群体选择概率趋向1的收敛速度成正比。而由图8可知,对高速公路使用者群体来说,经济奖励力度的改变对其选择概率演化趋势和收敛速度几乎无影响。
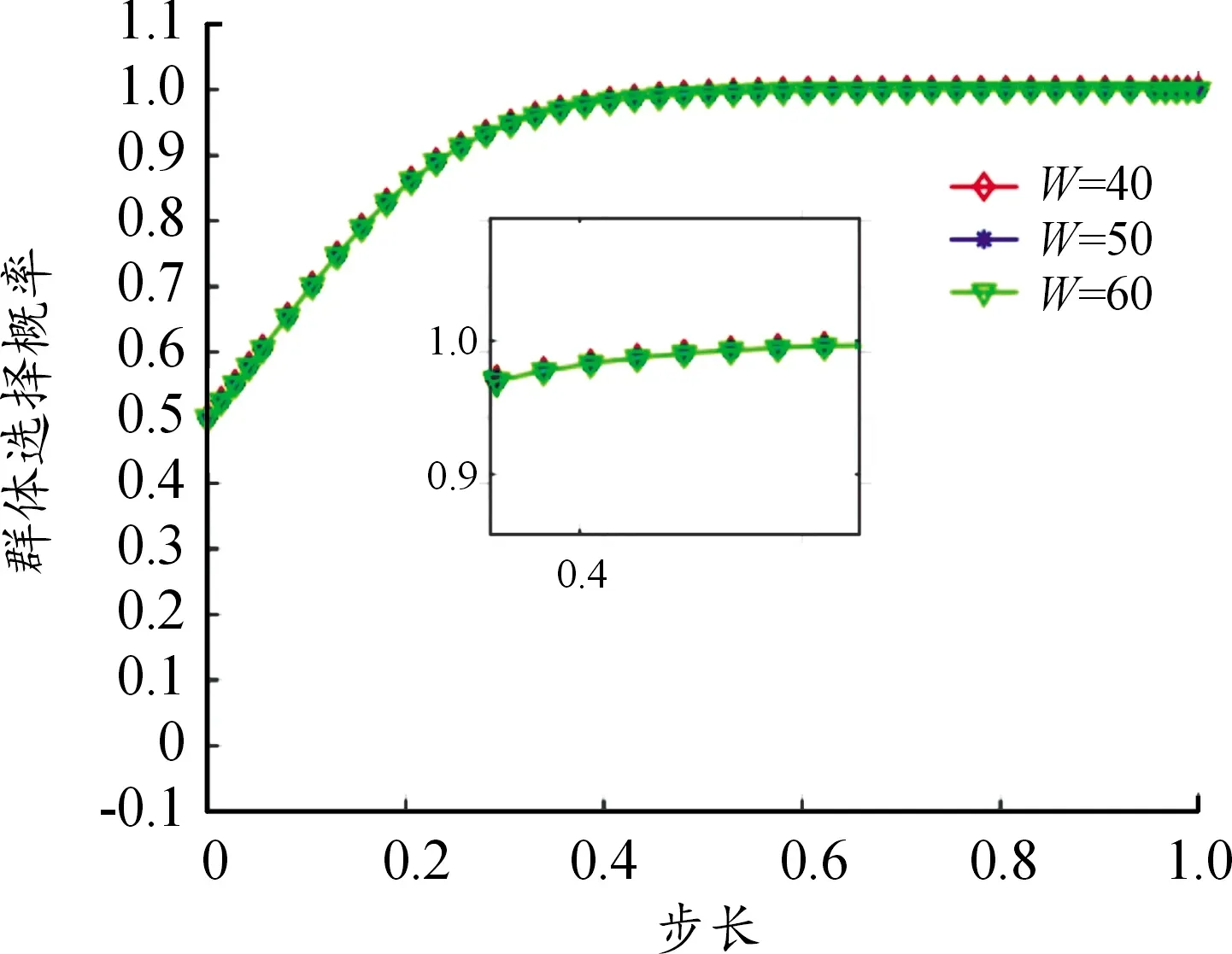
图8 W变化对高速公路使用者方演化影响曲线
3 结论
1) 博弈系统共有4个稳定条件下的均衡点,达到(1,1)状态(选择高速公路出行,做出差异化收费调整措施)的稳定性条件为-G1+G2-N2+N1-W+α1E+α1W-α2E<0且-ΔC+ΔR+β1E2-α1E1<0。
2) 高速公路拥堵率的降低对利益相关者群体做出高速公路出行和差异化收费调整行为策略的演化速率起明显的促进作用。高速公路经营者应优化前期设计阶段的道路线形,提高交通管理水平,让用户在选择高速公路时可以提升时间效益,降低出行成本。
3) 高速公路经营者的决策和高速公路使用者的行为是相互制约的,高速公路上级集团公司的直接经济奖励和社会公众的额外声誉奖励是激励高速公路经营者群体做出差异化收费调整措施、确保高速公路井然有序通行的有效保证和动力来源。
4) 通过带有时间变量的演化博弈分析,利用有效的交通管理手段控制双方博弈的均衡点,可实现整个路网的流量均衡分配,发挥高速公路的网络效益。
