考虑多指标博弈的电动汽车跟车控制
2022-04-15金智林
卢 静,金智林
(1.南京航空航天大学金城学院, 南京 210016;2.南京航空航天大学 能源与动力学院, 南京 210016)
自动跟车系统能够有效提高道路的通行效率与安全性、减轻传统驾驶员疲劳驾驶的操纵负担[1-4]。在交通拥堵时,跟车系统往往会控制车辆自动以小制动强度进行刹车,以一定的安全距离跟随前方车辆行驶。在上述过程中,电动汽车再生制动系统能够有效提高续航里程[5-6]。虽然电动汽车可通过驱动电机再生制动使车速降为0,但仅通过电机再生制动实际能够为车辆提供的瞬时最大制动减速度是有限的,而在跟车过程中,大制动强度的制动需求是客观存在的。也就是说,仅通过驱动电机进行制动不能实现大制动强度、短制动距离的制动,更不能实现急刹车等操作,因此不满足日常跟车时的制动需求(如前车急刹车)。例如:广泛应用在电动汽车上的由德国博世公司所研发的ESP hev系统,当整车控制器需求的制动强度小于0.3g时,制动力可完全由驱动电机提供,此时液压制动系统不参与工作;而当整车控制器需求的制动强度大于0.3g时,单独由驱动电机进行再生制动已无法满足需求,液压制动系统将会介入,与驱动电机再生制动共同为车辆提供制动力。因此,受限于驱动电机输出的最大力矩,在对于制动强度需求较高的工况下必须配合摩擦制动来保证跟车安全。此时,部分制动能量将以摩擦热能的形式损失,无法回收[7-10]。此外,大制动强度的跟车策略即紧急制动虽然能够提高跟车安全性,但会造成乘客的不舒适[11]。因此,如何在跟车工况下平衡各目标之间的博弈关系,对智慧物流等领域自动跟车控制的大规模推广意义重大[12]。
目前,传统燃油车自动跟车控制系统的经济性优化已趋于成熟[13-14]。相比传统燃油车,混合动力电动汽车和电动汽车更容易通过再生制动来设计节能控制策略,以提高车辆在跟车行驶过程中的制动经济性[15-17]。然而,上述研究并未考虑跟车工况下前方车辆运动学特性对被控车辆在进行跟车决策时的影响。受驱动电机能够输出的最大力矩的限制,制动系统的运行方式与交通环境的复杂程度密切相关,从而造成了车辆在频繁制动过程中的能量损失。因此,需要在设计跟车策略时将车辆间动力学特性与被控车辆能量回收机理相结合。
在目前的跟驰过程多目标决策控制研究中,模型预测控制因其动态协调优化能力而得到广泛应用[18-19]。在滚动优化过程中,理想的控制方法是根据交通环境动态调整各性能指标的权重系数。对于多个指标之间的冲突,通过建立博弈模型并求解其纳什均衡,可以得到各绩效指标的合理收益分配[20-22]。因此,在控制策略的设计中应考虑各指标之间的博弈关系。根据求解博弈模型得到的混合策略纳什均衡,确定各指标的权重,理论上能够有效实现跟车场景下被控车辆性能的动态调整。
针对上述问题,首先结合交通环境分析建立了制动能量传递模型和车间纵向模型,提出了混合策略下跟车场景中各博弈方纳什均衡的最优解方法。在此基础上,提出了基于跟车博弈模型混合策略纳什均衡的预测控制方法,通过制动力的分配和对前车纵向行为的预测,提高了被控车辆理论可回收制动能量占总制动能量的比例。
本文的主要贡献在于:提出了基于模型预测控制的多目标节能控制策略,实现了通过对前车制动行为的预测,根据工况动态调整模型预测控制器中指标的权重(权重动态调整的依据为当前采样时刻下被控车辆跟车博弈模型的混合策略纳什均衡,即各个参与者的偏好),从而实现提高制动能量回收效率,同时提高车辆续航能力、提高舒适性以及保证安全性的控制目标。
1 跟车场景数学建模
为了在控制器设计中定量地分析和控制车辆跟驰过程中的各项指标,建立了制动能量传递模型和交通环境中的车辆间纵向动力学数学模型。
1.1 制动能量传递模型
通过对制动过程中纵向力进行分析,得到车辆在制动过程中的总能量消耗[23],如式(1)所示:
(1)
式中:ΔE为制动过程中包括风阻等因素在内的总能量损失。也就是说,ΔE由2部分组成,一部分由于风阻、刹车片机械摩擦等因素以热能的形式消耗,无法回收;另一部分能量可以通过电机的再生制动转化为电能并储存起来。P为车辆的负载功率,v为制动过程中每个采样时刻的纵向车速,Ff为滚动阻力,Fw为风阻,Fb(zt)为包括再生制动力和摩擦制动力在内的总制动力,是制动强度zt的函数。
接下来从车轮到储能单元逐级分析了可回收能量在传输过程中的损失,提出了可回收能量的定量表达式,如式(2)所示:
(2)
式中:E为考虑传递过程损失后的理论可回收制动能,P4为储能单元瞬时功率,K1为机械传动机构的传递效率系数,K2为驱动电机再生制动能量转换系数,K3为储能单元的能量转换系数,Fb_re为驱动电机可提供的车轮上的再生制动力。
1.2 交通环境中车辆间纵向动力学数学模型

(3)
式中:ax_ego为当前时刻被控车辆的理想纵向加速度,Vx_ego为被控车辆的纵向速度,τ为控制系统的时滞常数。
以跟车过程中被控车辆与前方车辆的相对距离和相对速度误差为状态变量,建立跟车模型[24-26],如式(4)所示。

(4)
式中:Δv和d(t)为被控车辆和前车间的纵向相对速度和相对距离,可由传感器测得。dsafe(t)为理想安全距离,Δd为相对距离的跟踪误差。当安全距离过小时,在跟车过程中容易发生追尾事故。虽然长距离的安全距离可以保证跟车的安全,但会减少单位时间和单位道路长度的车辆数量。也就是说,从宏观上看,过长的安全距离降低了特定路段车辆的通行效率,这也是造成日常交通拥堵的主要原因之一。本文中的安全距离模型如式(5)所示。
dsafe(t)=thvx_ego+d0
(5)
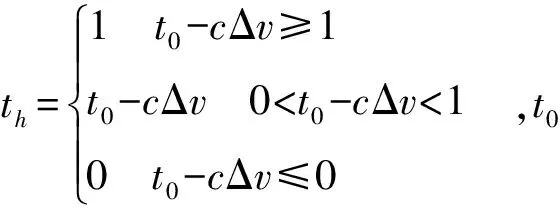
2 跟车过程多目标博弈控制
对制动能量回收效率、跟车安全性和制动舒适性3个主要指标之间的矛盾关系进行了分析,综合考虑多目标间的博弈关系,建立了跟车场景的博弈模型,并提出了混合策略纳什均衡求解方法,设计了跟车过程博弈控制策略。
2.1 跟车场景的博弈模型
通过对电动汽车跟车过程进行分析,构建了安全性、舒适性和节能性3个跟车决策过程中的评价指标,3个指标作为博弈模型参与者时的决策收益定性描述为:
1) 安全性参与者
若一旦发现跟车距离小于阈值,此时收益最大的决策为输出最大制动减速度,使被控车辆进行紧急制动,则可以最大程度地避免碰撞的发生。
2) 舒适性参与者
当制动减速度过大即车辆急刹车时,必然造成乘客的不舒适,因此,收益最大的决策为任何时候都采取尽量小的制动减速度。
3) 节能性参与者
当理想制动减速度较小时,仅通过电机再生制动即可满足需求,此时理论上所有制动能量都是可回收能量;而当理想制动减速度较大时,仅通过电机再生制动无法满足需求,需要摩擦制动介入来使实际总制动强度达到理想值。然而,此时必然有一部分能量以热能的形式散失,无法被回收。因此,收益最大的决策也为任何时候都采取尽量小的制动减速度。
由上述分析可见,任何时候都采取尽量小的制动减速度这种决策,对于舒适性和节能性来说都是收益最大的决策,但对于安全性来说,采取尽量小的制动减速度这种策略收益很小甚至收益为负,即会导致碰撞,反之亦然。3个指标间的博弈关系如图1所示。
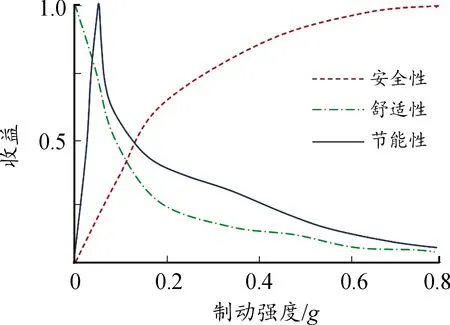
图1 3个指标间的博弈关系曲线
制动能量回收效率指标如式(6)所示,用于衡量理论可回收能量占总制动能量的比例。
(6)
式中:E为可回收制动能量,ΔE为总制动能量,η为可回收制动能量占总制动能量的比例。由此可见,当指标值η较低时,在多目标优化控制器中增加指标的权重系数,可以迫使优化器获得较小的制动强度,从而达到提高理论可回收制动能量占总能量比例的目的。但从前面的分析来看,制动强度过低会影响跟车安全。因此,在滚动优化控制器中,需要通过博弈模型动态确定指标的权重系数。综上所述,在博弈模型中,将制动能量回收效率定义为参与者1,其收益函数如式(7)所示。
u1(zt)=a1ηN+b1
(7)
式中:u1(zt)为制动能量回收效率收益函数,a1和b1为超参数。
与制动经济性相比,在设计制动舒适性收益时,不仅要考虑成本函数的现值,还要考虑成本函数的积分值。也就是说,制动舒适性指数允许在短时间内增加,但不允许长时间处于较高的状态。综上所述,在博弈模型中,将制动舒适性定义为参与者2,博弈模型中参与者2的收益函数设计如式(8)所示。
(8)
式中:u2(zt,zt-1)为制动舒适性收益函数,zt-1为被控车辆在t-1时刻的制动强度,ts为策略执行时间(即执行器的采样时间)。在这项工作中,模拟验证和试验车辆的控制器采样时间为100 ms,a21、a22和b2为超参数。
对于汽车跟驰安全而言,其收益不仅是制动强度的函数,而且受交通环境中相对速度和距离的影响。因此,在博弈模型中,将汽车跟驰安全性定义为参与者3,参与者3的收益函数如式(9)所示。
(9)
式中:ΔV和Δdt分别为当前采样时刻下被控车辆与前车之间的相对速度和相对距离,g为重力加速度,取9.8 m/s2,a3和b3为超参数。
上述问题被转换为包含有限个参与人的博弈模型策略求解问题。对于有限个参与人的非合作博弈来说,其策略的一般形式Γ如式(10)所示。
(10)
式中:N为博弈过程参与者个数,在本文中为跟车过程中的安全性、舒适性和节能性3个参与者;Si为第i个参与者的策略偏好,即在当前采样时刻下其对于制动强度的偏好;ui为当前采样时刻下第i个参与者采取相应的策略时所能够获得的收益;S为由所有参与者的策略所构成的策略集合。
而对于混合策略博弈模型来说,其纳什均衡必然存在,纯策略只是混合策略的一个特例。当前混合策略下参与者i的收益是纯策略收益和混合策略的乘积之和[27-28]。因此,如果玩家i的最优收益被记录为βi、参与人i的混合策略求解问题转换为如式(11)所示的优化问题。
(11)

2.2 多目标节能控制策略
提出了基于博弈模型混合策略纳什均衡的预测控制跟车控制策略,并通过博弈模型动态求解目标权重,以平衡再生制动能量回收效率、跟车安全性和制动舒适性之间的矛盾。
控制策略的核心思想为根据博弈模型的输出,对再生制动力和摩擦制动力进行分配,提高再生制动力占总制动力的比例,从而提高理论上可回收制动能量占总制动能量比例,如图2所示。首先,将跟车过程中的安全性、舒适性和节能性视为跟车博弈过程的3个参与者,构建博弈模型,通过求解上述博弈模型的混合策略纳什均衡,得到当前采样时刻下模型预测跟车控制器中优化目标所需的目标函数权重系数。
其次,通过安全性、舒适性和节能性3个指标建立优化模型,基于模型预测控制在每个采样时刻对理想的被控车辆的理想制动强度进行计算。在每个采样时刻,将博弈模型求解得到的权重系数赋值给模型预测跟车控制器中优化模型的3个优化目标,以实现根据博弈模型参与者对于策略的偏好,来对跟车过程的决策进行调整,从而得到当前时刻理想的被控车辆制动强度,输出到理想制动强度跟踪控制器。
得到目标制动强度之后,再对目标制动强度进行跟踪控制,具体控制的过程如下:将目标压力制动强度与实际制动强度做差得到Δz,输入到跟踪控制器中,跟踪控制器分别决策出再生制动系统驱动电机和液压制动系统电磁阀的PWM占空比,通过PWM产生模块,输出给定占空比的PWM信号,通过驱动板进行功率放大后控制驱动电机和线性阀的开关,以产生所需要的目标轮缸压力。轮缸压力传感器采集当前的实际轮缸压力,通过A/D 采集模块为跟踪控制器提供反馈,由此实现一个闭环控制回路。
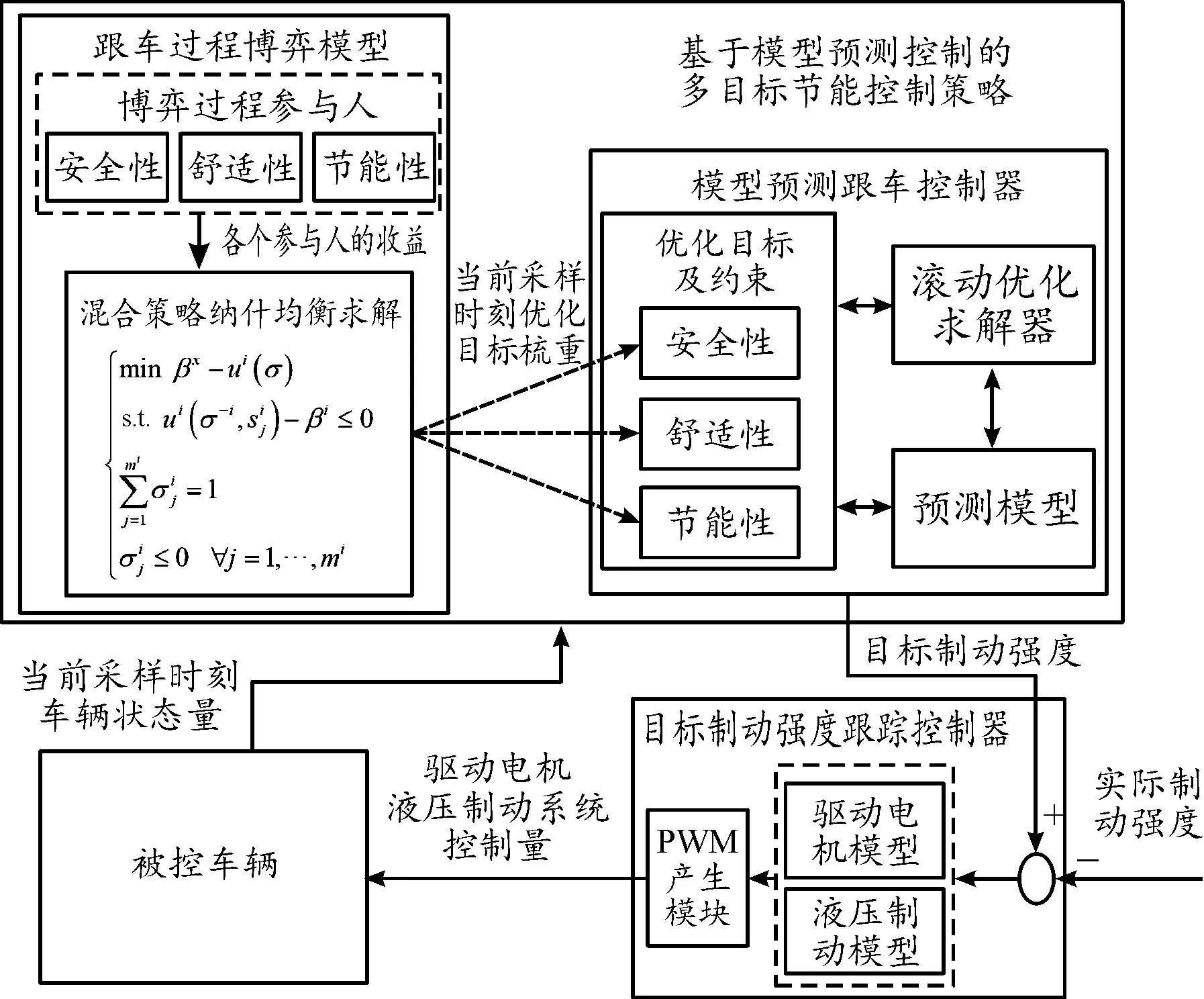
图2 多目标节能控制策略框图
首先,利用混合策略纳什均衡在每个采样时刻构造参与方i的权重,并作为自变量实现对各指标的调整,如式(12)所示。
Gi(k)=gi·find[σi[max(σi(k))]]
(12)
然后,通过量化性能指标函数并将权重系数集成到全局成本函数中,建立在线滚动时域优化问题。车辆间离散状态空间如式(13)所示。
X(k+1)=AdX(k)+Bdu(k)
(13)

在模型预测跟车控制器的每一次循环中,通过预测模型实现根据跟车模型的历史相对车速、相对距离信息输入,对被控车辆未来的制动减速度输出序列进行预测,即最终模型输出的是制动减速度序列,并将序列中的第一个元素取出作用在被控车辆上,再进入下一次循环。在不考虑滚动优化阶段加权计算的情况下,预测模型的预测输出如式(14)所示。
Y(k)=ψ(k)ξ(k)+θ(k)ΔU(k)
(14)
式中:
Y(k)为k时刻预测模型的输出向量,Np为预测时域,Nc为控制时域,η(k+i)为第k+i时刻的预测值误差,其中i∈(1,Np),η(k+i)表达式如式(15)所示。
(15)
式中:ηd(k+i)和ηv(k+i)分别为第k+i时刻相对距离和相对速度的预测值误差,Δd(k+i)p和Δv(k+i)p分别为第k+i时刻由预测模型得到的相对距离和相对速度的预测值,Δdi(k+i)和Δvi(k+i)分别为第k+i时刻由动力学模型计算得到的相对距离和相对速度的理想值。
而在滚动优化过程中,根据对跟车过程中的博弈节能设计,在每个采样时刻,跟车博弈模型的输出为滚动优化过程中优化目标的权重系数。而对于安全性参与者来说,由于在预测模型中,相对速度、相对距离误差均为长度为NP的序列,即考虑预测时域内前车制动行为的序列,因此在优化过程中需要加以相应的权重系数,对于安全性参与者的收益函数进行改写得到如式(16)所示。
(16)
式中,i∈(1,Np)。
根据以上分析,建立了采样时间k时的制动经济性指标和舒适性指标,如式(17)所示。
(17)
然后,将上述优化问题转化为预测形式,并在每个采样时刻进行求解。在每个采样周期内,系统根据当前状态预测未来车辆信息,求解二次优化问题,得到最优控制序列,如式(18)所示。
(18)
3 试验结果分析
为了验证跟车控制策略的有效性,同时考虑到实车道路试验的风险,建立了半实物试验平台,如图2所示。测试系统以NI PXI实时操作系统为核心,基于CarSim软件和LabVIEW软件的联合仿真,构建虚拟跟车交通环境,实现完整的整车硬件在环跟车仿真环境。该测试平台主要分为2部分,分别为上下位机和底层执行机构,其中上位机为工控机,运行人机交互软件,进行系统状态监控和数据存储;下位机为NI PXI,一方面,CarSim构建的整车动力学模型在下位机实时运行,向本文提出的跟车控制算法模块实时提供整车状态参数,另一方面,基于快速原型,利用Matlab/Simulink开发跟车控制算法,控制算法在接收到环境信息及车辆参数,向底层控制器发送制动控制指令;底层执行机构主要包括电驱动系统、制动系统和传感器模拟系统,底层控制器接收到上层算法的控制信号,基于底层算法,精确控制执行机构响应,并利用传感器反馈于车辆动力学模型,实现闭环仿真模拟。

图3 半实物仿真试验平台示意图
该平台的主要创新之处在于实现了试验平台与虚拟跟车交通环境的闭环仿真,并以典型工况纽约循环(NEDC)为例,比较了本文提出算法与目标权重确定的基本MPC算法的差异。
3.1 本算法与基本MPC算法的差异性分析
为进一步说明本算法与基本MPC算法的差异性,对前车静止的极端情况进行分析,在仿真开始时刻被控车辆与前车相距100 m。仿真结果如图4所示,可得相比现有控制策略,本文提出的方法实际上改变了现有跟车策略的决策方式。也就是说,现有的决策方式是以跟随性为主导,实现的效果为被控车辆紧紧跟随前车的动作。这样带来的不足是没有对前车的行为进行预测,不可避免地会有急刹车等大制动强度的决策,从而造成制动能量的浪费和不舒适。而本文提出的方法通过对安全性、舒适性和节能性3个指标的博弈,直观地来看拉长了被控车辆与前车之间的相对距离,同时也带来了相对速度的跟踪不像现有技术一样让被控车辆的车速十分精确地跟踪前车车速。但这样的好处是当前车一旦出现紧急制动等行为时,被控车辆仍可以相对较小的制动强度进行制动,从而尽可能的保证舒适性和制动能量回收效率。

图4 跟随过程相对距离、相对速度曲线
3.2 节能控制性能分析
对瞬时再生制动功率和回收能量进行分析,如图5、图6所示。由图5可以看出,与指标权重固定的基本MPC算法相比,本文提出算法得到的瞬时再生制动功率平均值提高了18.25%。由图6可以看出,在循环结束时,回收的制动能量提高了13.4%。
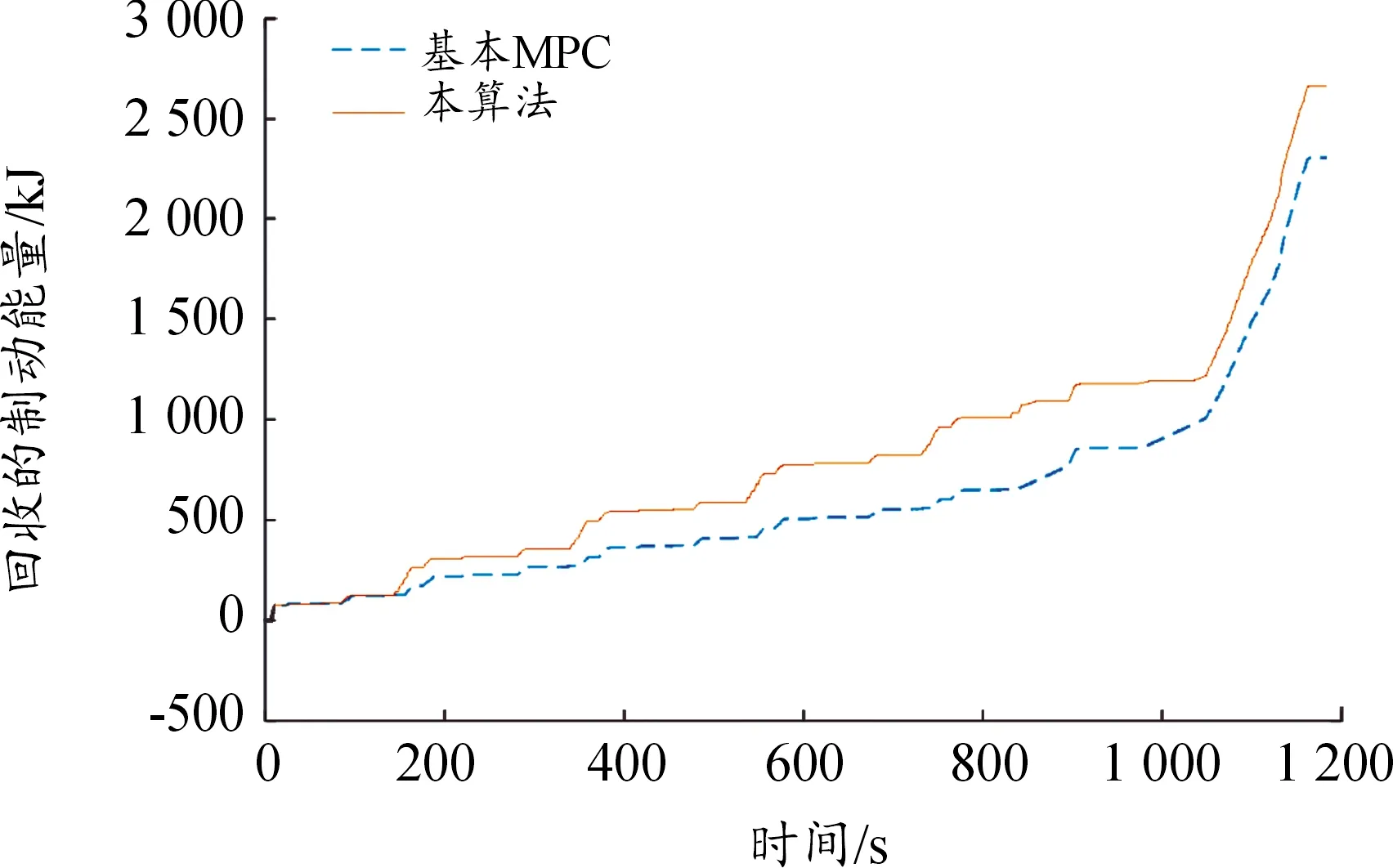
图6 回收的制动能量曲线
3.3 安全性能分析
根据HIL测试结果,对本文提出算法的跟车安全性进行了分析,证明了本文提出算法在整体性能上的优越性。当前车执行NEDC循环时,被控车辆和前车之间的相对速度和距离如图7、图8所示。相对速度方差和相对距离期望值见表1。与指标权重固定的基本MPC算法相比,本文提出算法的相对速度方差平均提高了15.89%。这是因为当被控车辆处于紧急制动时,采用提出算法得到的被控车辆速度变化率较小,因此相对速度的变化率较大。
而在相对距离方面,本文提出算法平均提高了58.37%。本文提出算法的相对速度跟随性能相对较差,但由于有足够的安全裕度,仍能有效地保证跟车安全。本文提出算法的相对速度跟随性能相对较差,但由于有足够的安全裕度,仍能有效地保证跟车安全。

图7 试验过程中的跟车相对速度曲线
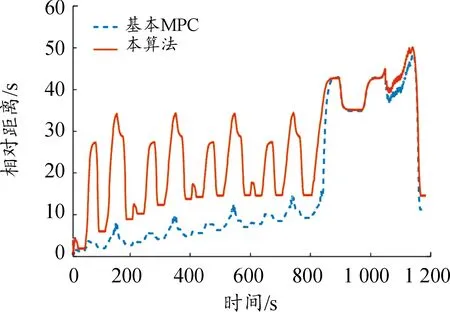
图8 试验过程中的跟车相对距离曲线

表1 跟车过程中的平均相对距离和相对速度方差
3.4 舒适性能分析
在制动舒适性方面,前车执行NEDC循环时,计算被控车辆舒适性性能指标及其积分值,如图9、图10所示。

图9 本文提出算法试验结果曲线

图10 指标权重固定的基本MPC算法试验结果曲线
与指标权重固定的基本MPC算法相比,在循环结束时,舒适度指数的积分值降低了49.15%。因此,在相同的试验条件下,该方法不仅有效地提高了制动能量回收效率,而且显著地优化了跟车场景下被控车辆的制动舒适性。
4 结论
为了提高跟车场景下制动能量回收效率,揭示了电动汽车制动能量回收特性与车间纵向动力学的博弈关系,提出了一种基于跟车博弈模型混合策略纳什均衡的预测控制方法。该算法能在跟车过程中尽可能地提高被控车辆的再生制动能量回收效率,同时保证在前车紧急制动条件下的跟车安全性和制动舒适性。
未来的研究将集中在以下两个方面:一是改进算法设计以及制动模式切换策略,提高博弈模型求解和模型预测控制系统动态求解的整体运行效率。其次,在合法许可和测试安全的前提下进行道路测试,进一步验证算法的有效性。
