高围压作用下堆石体剪切带形成及相关细观结构演变

2022-04-15吴相豪梁冰寒华香玉

长江科学院院报 2022年4期

吴相豪，梁冰寒，华香玉

(上海海事大学海洋科学与工程学院，上海 201306)

1 研究背景

堆石坝由于造价低、施工速度快,以及对地形、地质条件要求低等优点被广泛应用于坝工领域。在我国堆石坝坝高已实现由200 m向300 m级的跨越，如双江口心墙堆石坝最大坝高为314 m、其宗心墙堆石坝最大坝高为356 m。随着坝高的不断增加，堆石料破碎现象更加严重，势必影响坝体内部高应力区堆石体的变形特性，研究这种应变局部化或剪切带的形成对评估土木工程结构的稳定性很重要。近年来国内外学者采用室内试验、理论研究和数值模拟手段研究颗粒材料剪切带的形成和演变。在室内试验方面，许多学者采用真三轴试验[1-2]、环剪试验[3]、常规三轴试验[4]和平面应变试验[5-6]来研究剪切带的形成和演变，借助先进的宏观量测技术[7]和粒子图像测速法[8]等手段分析剪切带的产生、发展和演化过程。这些试验揭示剪切带的形成受到孔隙率、颗粒形状、围压水平、固有应力诱发的各向异性等多种因素的影响。

在理论研究[9-12]方面，学者主要研究剪切带产生及其发展的过程，包括本构关系模型的研究和剪切带形成方向的研究。李宏儒等[9]研究了结构性黄二元介质模型在局部化剪切带中的应用，再现了剪切带萌生和发展的过程；Roscoc[13]研究了剪切带的倾角，认为剪切带沿零拉伸方向发展。

在数值模拟方面，许多学者采用离散元法建模，获得颗粒滑动、旋转和破碎等颗粒材料的微观特征，探究剪切带的形成机理。周健等[14]采用单一的圆形颗粒单元模拟砂土和黏性土的剪切带的形成与发展；刘君等[15]通过簇颗粒方法模拟堆石料的双轴试验，得到颗粒破碎的细观演化规律和剪切带的分布范围；孙德安等[16]研究了不同路径下剪切带的数值模拟；张强等[17]利用计算机三维扫描与随机模拟技术构造出三维土石混合体离散元模型，研究了土石混合体剪切带的形成机理及分布形态；Zhou等[18]提出了不规则形状的可破碎颗粒组件的离散元建模，探索了颗粒可破碎性在颗粒材料的剪切带中的作用；Gu等[19]利用双轴数值试验研究了初始密度和围压对剪切带特性的影响；Ma等[20]利用离散元模型(DEM)方法构造出不规则和易碎的颗粒模型，将剪切带与微观结构的演变联系起来。上述研究成果为深入分析高应力区堆石体的变形特性奠定了理论基础。

针对堆石料具有形状不规则、多棱角和易破碎等特点，本文基于颗粒流理论，构造3种不同形状的颗粒簇，建立堆石体数值试样，进行双轴压缩颗粒流模拟试验，以期能够再现高应力区堆石体变形过程，在此基础上探讨高围压作用下堆石体中剪切带形成及相关细观结构演变规律。

2 堆石体数值试样生成过程

2.1 颗粒材料接触模型

PFC软件中颗粒材料接触模型分为接触黏结模型和平行黏结模型。接触黏结模型可视为一个点胶结，当该接触处的拉应力或者剪应力超过了接触黏结的极限值，黏结发生破坏，但颗粒间的接触刚度仍然有效，接触黏结为点接触，无法抵抗弯矩的作用。平行黏结模型能够模拟2个圆盘间胶凝性材料的力学行为，可视为一组以接触点为圆心均匀分布在接触圆断面的弹簧，该组弹簧的切向刚度和法向刚度均为常值，平行黏结为面接触，可以传递力和力矩。与接触黏结模型相比，平行黏结模型更能反映岩石材料破坏的力学特性[21]，体现堆石料的破碎问题。

本文采用颗粒簇模拟堆石料，采用了颗粒黏结模型(BPM)[22-24]模拟堆石料的颗粒破碎，通过颗粒簇内部颗粒间黏结键断裂模拟堆石料破碎进而探讨堆石体剪切带形成及相关细观结构演变规律。颗粒簇内部各颗粒之间的接触选用平行黏结模型，颗粒簇与颗粒簇之间的接触以及颗粒簇与墙体之间的接触均选用接触黏结模型，如图1所示，实线表示颗粒簇内部颗粒之间的平行黏结，虚线表示颗粒簇之间以及颗粒簇与墙体之间的接触黏结。

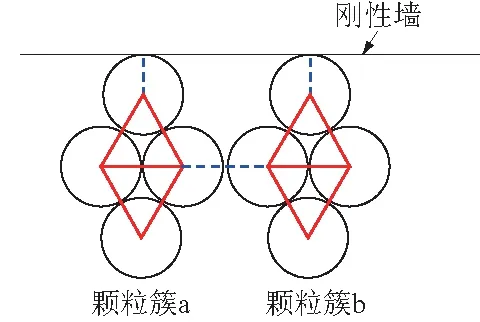
图1 颗粒材料接触模型Fig.1 Contact model ofgranular materials

2.2 颗粒簇构造

考虑到堆石料形状不规则、多棱角，本文通过自编程序构造出3种不同形状的颗粒簇，如图2所示，其中颗粒簇内部孔隙的面积属于颗粒簇的实体面积。颗粒簇由圆盘颗粒通过平行黏结模型黏结而成，图2中实线表示黏结键，相邻圆盘颗粒两两相切避免重叠，否则黏结键破坏会释放能量，导致结果失真，其算法公式为

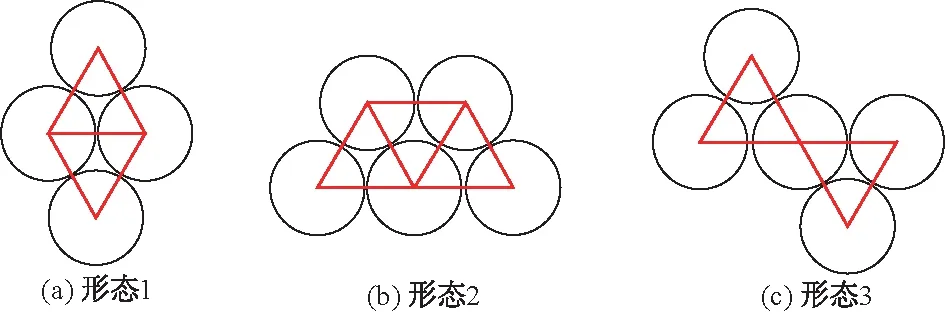
图2 颗粒簇Fig.2 Particle clusters

(1)

式中：xc、yc为母球的圆心坐标；xk、yk为子球的圆心坐标；d为子球圆心到母球圆心的距离；θk为子球圆心坐标对应母球的圆心坐标的随机角度，保证生成子球的位置随机； rand为[0，1]的随机数。

2.3 堆石体数值试样

堆石体数值试样采用半径膨胀法制备[25]。颗粒数量直接影响计算时间，受计算规模的影响，采用周健等[26]在模拟过程中将颗粒的尺寸放大的方法，生成的颗粒数量在8 000～10 000之间，既满足计算精度又缩短了计算时间，根据刘海涛等[27]对粗粒土尺寸效应的离散元分析确定试样宽6 m,高12 m。在宽6 m、高12 m的长方形二维空间内随机生成圆盘颗粒，圆盘颗粒初始半径控制在18～22 cm之间，按均匀级配成2 000个圆盘颗粒，充分循环计算使圆盘颗粒到达平衡状态，并记录圆盘颗粒的位置和半径；然后删除圆盘颗粒，根据记录的数据随机生成与圆盘颗粒粒径相同的颗粒簇，如图3所示，圆盘颗粒内部为颗粒簇；最后通过程序算法以极小的膨胀系数控制颗粒半径逐渐膨胀，在膨胀过程中，允许颗粒移动调整，避免颗粒间出现重叠和不平衡力，为保证试样的密实性与均匀性，颗粒间的摩擦系数f暂时设置为0[28-29]，一旦达到指定孔隙率，循环结束，颗粒间的摩擦系数恢复正常值，试样再次循环计算至平衡状态。

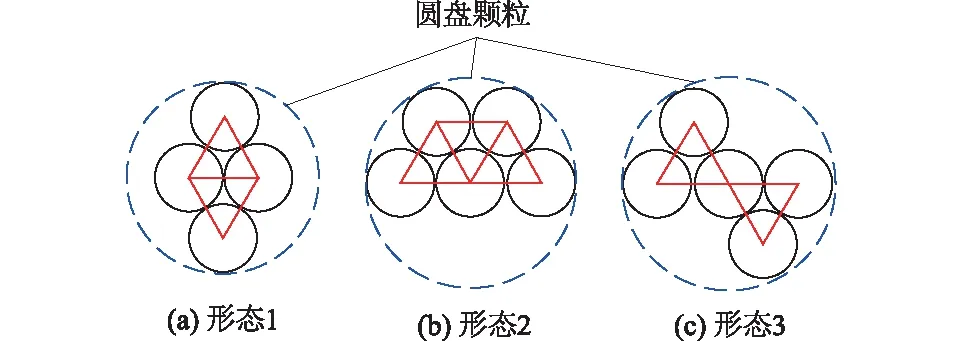
图3 试样颗粒簇构造Fig.3 Particle cluster structure of sample

初始时颗粒形状为纯球形颗粒，在球形颗粒外轮廓范围内替换为文中图2的颗粒形状时必然会产生面积损失，达到指定孔隙率后，颗粒簇模型最终半径范围为10～15 cm，2 000个颗粒簇模型由9 333个颗粒组成，共有11 999个平行黏结键。

孔隙率参考文献[30]，通过2次调整颗粒的摩擦系数，使试样在围压4.0 MPa下达到平衡并得到试样最终的孔隙率，其值为0.197。堆石体数值试样如图4所示。通过伺服机制赋予四周墙体速度，不断地循环调整达到指定围压，此时，试样处于初始状态，可以进行固结加载，加载过程中控制上下墙体以0.01 m/s的加荷速率相对移动，同时通过伺服机制使两侧墙体保持围压不变，记录下监测信息。

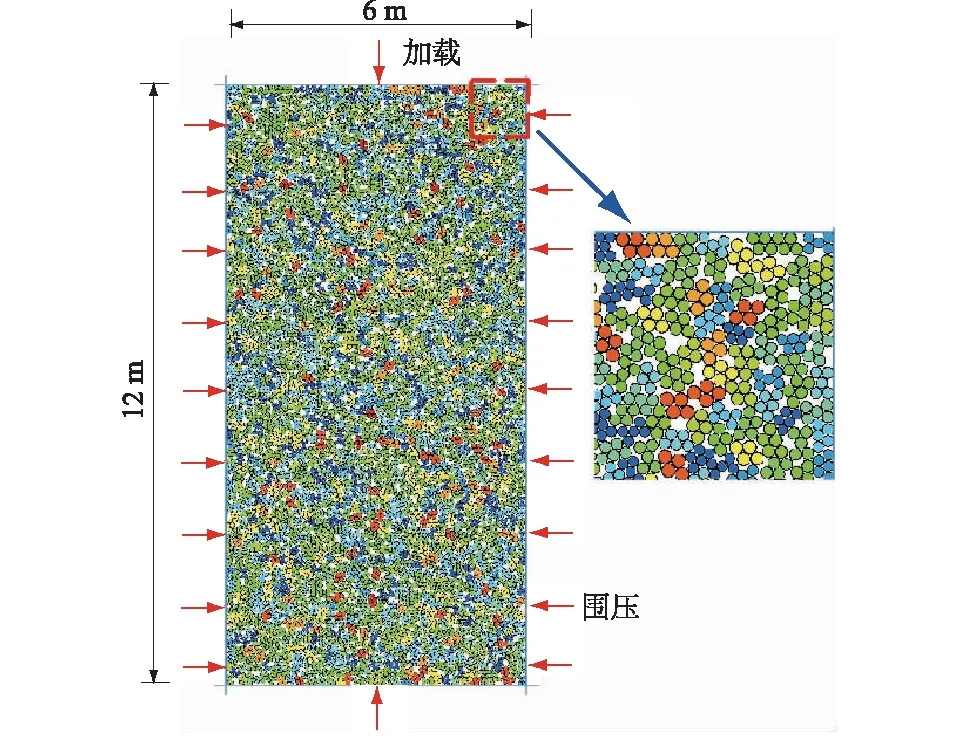
图4 堆石体数值试样Fig.4 Numerical sample of rockfill

3 数值模拟试验

3.1 数据来源

Belheine等[29]、常在等[30]和刘恩龙等[31]对堆石料进行了固结应力从0.4～4.0 MPa的压缩试验，研究了堆石料的临界状态与考虑颗粒破碎的本构模型。试验所用土料是长河坝的主堆石料，为硬质闪长岩，颗粒相对密度为2.82，采用干法制样，最大粒径为60 mm，压缩试验获得的应力-应变曲线如图5所示，本文数值模拟试验围压设置为4.0 MPa。

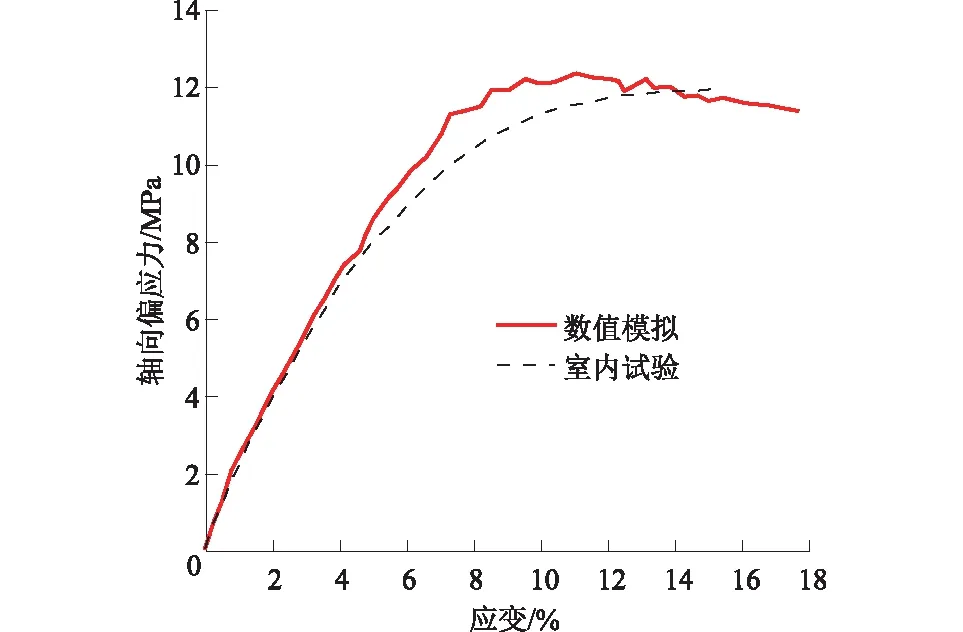
图5 数值模拟试验与室内试验结果对比Fig.5 Comparison between numerical simulation testand indoor test results

3.2 细观参数选取

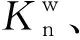
本文通过自编程序赋予每一颗粒簇不同的黏结强度，即Bn、Bs在某一区间内随机取值，其算法公式为

(2)

其中：B′n=B′s=4.2×103kN；λ=0.5×103kN；rand为随机数，取[0,1]。

为了与文献[31]的试验曲线相匹配，使用参数校准程序[32]不断调整细观参数,进行颗粒流模拟试验，直至颗粒流模拟试验结果与文献[31]的试验结果基本一致，见图5所示。最终选取的细观参数见表1。

表1 颗粒流模拟细观参数Table 1 Mesoscopic parameters of particle flow simulation

3.3 荷载的施加

颗粒流模拟试验是通过一套数值伺服系统让顶部和底部墙体作相对运动来施加荷载，同时调整两侧墙体位移，以保持围压稳定。

4 试验结果与分析

采用表1所示的围压和细观参数进行颗粒流模拟压缩试验，在试验过程中跟踪颗粒流模型中颗粒簇的旋转、位移、破碎，以及孔隙率等堆石体细观结构，据此研究高围压作用下堆石体中剪切带的形成及相关细观结构的演变规律。

4.1 颗粒簇旋转过程

图6为数值模拟试验得到的不同应变下颗粒簇旋转云图，图中红色代表颗粒簇沿顺时针方向旋转，旋转角度>30°，蓝色代表颗粒簇沿逆时针方向旋转，旋转角度>30°。

图6 不同应变下颗粒簇旋转云图Fig.6 Cloud of particle cluster rotation underdifferent strains

图6显示，轴向应变为2%时，试样中旋转角度>30°的颗粒簇较少，且分布比较均匀；随着荷载增加，轴向应变也不断增大，轴向应变为6%时，试样中旋转角度>30°的颗粒簇增多，分布比较集中，潜在的剪切带沿着试样的对角线出现；轴向应变为10%时，试样中旋转角度>30°的颗粒簇的分布位于2条主要剪切带，隐约可见X形剪切带；随着模拟试验继续进行，在轴向应变为14%和18%的颗粒簇旋转云图上，一些局部区域的旋转角度>30°的颗粒簇开始消失，清晰可见X形剪切带，但轴向应变为18%的试样中2条主要剪切带带宽小于轴向应变为14%的剪切带带宽。

4.2 颗粒簇移动过程

图7为数值模拟试验得到的不同应变下颗粒簇位移云图，图中红色代表颗粒簇位移量最大，蓝色代表颗粒簇位移量最小。

图7 不同应变下颗粒簇位移云图Fig.7 Clouds of particle cluster displacement underdifferent strains

由图7可知，试样中颗粒簇沿2种轨迹移动：一种是试样上部、下部靠近加载装置的颗粒簇沿着轴向压力方向向试样中部移动；另一种是试样中间部位的颗粒簇向试样两侧移动。随着轴向应变的增加，颗粒簇移动轨迹表现出明显的规律性。轴向应变为2%时，颗粒簇沿着轴向力方向向试样中间移动，颗粒簇移动以压缩为主，试样表现为体缩；轴向应变为6%时，试样中部颗粒簇开始向两侧移动，说明试样由体缩向体胀过渡；轴向应变增大到10%以后，试样中间部位的颗粒簇沿着与水平方向成30°～45°的带状区域向两侧移动，说明试样内部发生了结构性变化。

4.3 颗粒簇破碎过程

本文颗粒簇由平行黏结键将多个圆盘颗粒黏结而成。圆盘颗粒间完整的黏结键见图2所示，当圆盘颗粒所受荷载超过圆盘颗粒间的黏结强度时黏结键断裂，颗粒簇发生破碎。

图8为圆盘颗粒间黏结键的断裂个数与轴向应变之间的关系曲线，图8中每根条柱的宽度代表0.5%的轴向应变，高度代表圆盘颗粒间黏结键断裂的个数。由图8可知，随着轴向应变增大，圆盘颗粒间黏结键的断裂个数不断增加，在轴向应变为9%时，黏结键断裂个数达到最大值，大量的颗粒簇破碎出现在应力峰值前一时刻，随后颗粒簇破碎的速度逐渐减弱。试样颗粒簇破碎过程与其宏观应力的发展同步，随着应变的增大，应力达到峰值之后降低，颗粒簇黏结键断裂个数也随之降低。

图8 黏结键断裂个数与轴向应变之间的关系Fig.8 Relationship between the number of bondfractures and axial strain

图9为不同应变下破碎颗粒簇分布情况，图中白色代表破碎颗粒簇。由图9可知，轴向应变为2%时，试样中没有白色区域，颗粒簇没有破碎；轴向应变增大到6%以后，随着轴向应变的增大，试样中白色的X形剪切带逐渐清晰，X形剪切带内的颗粒簇破碎严重。比较图6和图9可以发现，破碎颗粒簇的分布与旋转角度>30°的颗粒簇的分布基本一致，呈非对称的X形剪切带。

图9 不同应变下破碎颗粒簇分布情况Fig.9 Distribution of broken particle clusters underdifferent strains

4.4 试样孔隙率变化过程

图10为试样整体孔隙率与轴向应变之间的关系曲线。其中整体孔隙率n计算公式为

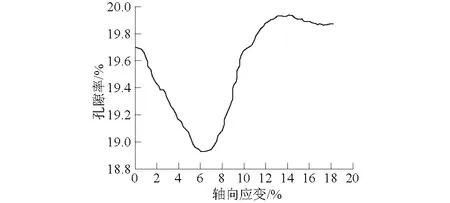
图10 孔隙率与轴向应变之间的关系曲线Fig.10 Relationship between porosity and axial strain

(3)

式中：A总为长方形容器随程序加载不断变化的面积;A球为所有球形面积以及颗粒簇内部孔隙的面积。

由图10可知，随轴向应变的增加，试样孔隙率先减小后增大，拐点对应的轴向应变约为6%。轴向应变<6%时，随轴向应变增大，试样孔隙率逐渐减小，表现为体缩阶段;在峰值之后试样处于应变软化阶段，剪切带之外的颗粒簇充分滑移旋转，位置相对稳定，而剪切带的宽度又在逐渐变小，因此整体孔隙率又开始出现下降的现象。试验结果与图7反映的结果基本一致。

在试样不同位置布置的测量圆如图11所示，监测每一个测量圆的位置坐标和孔隙率，根据这些数据生成不同应变下试样孔隙率分布云图，如图12所示，剪切过程中试样尺寸发生变化，测量圆的位置不变，红色代表孔隙率>0.197。

图11 测量圆分布Fig.11 Distribution ofmeasuring circles

图12 不同应变下孔隙率分布云图Fig.12 Porosity distribution under different strains

由图12可以看出，轴向应变<6%时，孔隙率>0.197的区域比较少，分布比较均匀，且随着轴向应变的增大，孔隙率>0.197的区域逐渐减少;轴向应变达到6%以后，随着轴向应变的增大，孔隙率>0.197的区域逐渐增多；轴向应变>14%时，一些局部孔隙率>0.197的区域开始消失，清晰可见X形剪切带，试验结果与图6、图9反映的结果基本一致。

4.5 剪切带形成的细观机制

由4.1—4.4节的分析可知，在颗粒流模拟压缩试验过程中，首先是颗粒簇相互挤压，颗粒簇发生自身的弹性变形，随着荷载持续增加，大小颗粒簇开始相互嵌入，试样孔隙率减小，表现出体缩趋势；当颗粒簇挤密到一定程度之后，颗粒簇间接触力迅速增大，开始发生少量的颗粒簇破碎，颗粒簇开始位置调整和重排，试样呈现体胀趋势。

随着试样进一步加载，颗粒不断地调整移动而且破碎的颗粒簇越来越多，试样中的颗粒簇开始发生错动和翻越，不断发生结构性调整，使得局部区域的颗粒簇被再次挤密，而位于试样对角线处的大量颗粒簇发生破碎、错动和翻越，形成孔隙率大、抗剪能力低的非对称X形剪切带。