基于SWAT模型的巴勒更河流域降雨-径流关系

李 凯，王永强，许继军，吴志俊,2，许 翔,2

(1.长江科学院 水资源综合利用研究所，武汉 430010； 2.河海大学 水文水资源学院，南京 210098)

1 研究背景

径流的主要来源是降雨，降雨的变化通常会直接导致径流改变。自19世纪以来，全球范围内的气温普遍升高，加剧陆地和海洋水循环过程，同时导致区域降雨和空间分布格局发生变化。此外，人类活动的不断增强，一方面导致蒸发、入渗、产流和汇流等水文过程发生改变，另一方面导致流域降雨-径流关系发生显著性的改变[1]。为揭示巴勒更河流域降雨-径流关系变化特征，研究其在时间上的演变机理，定量分离导致径流变化的影响因素的贡献率，对合理进行流域水资源管理开发、掌握流域水循环机理等方面有着重要的理论价值和意义。

自1940年代以来，国内外水文学家对降雨-径流关系开展了大量研究[2-3]。通过蓄水容量曲线能够有效研究降雨与径流关系，该方法以严格的物理学概念为基础，且与流域水平衡方程相吻合[4]。另有研究指出，降雨-径流在时空上具有动态和复杂的结构，建立多变量广义自回归条件异方差模型同样可以有效表示降雨-径流的方差-协方差随时间变化的关系[5]。李致家等[6]通过在全国15个典型流域建立地面径流相关图，分析区域降雨-径流关系。陈利者等[7]在上述工作的基础上做了进一步研究，在不对地下水进行分割情况下，首先构建流域降雨-径流相关图，重新分析其降雨-径流关系。近年来，降雨、径流研究热点主要集中在气候变化和人类活动影响下的降雨-径流关系，分析方法主要有2种，即定性方法和定量方法。其中，徐东霞等[8]利用嫩江流域近50 a的资料定性分析降雨-径流变化因素，得出的结论是径流变化主要是受到降雨变化的影响。郭爱军等[9]采用累积斜率变化率比较方法定量分离气候变化与人类活动对泾河径流的影响。然而，对一些无径流资料或缺少序列径流资料的地区如何研究降雨-径流关系是一个有待解决的难题[10]。目前，无资料地区径流估算主要是利用水文比拟法、集总式水文模型、分布式水文模型开展水文模拟，水文比拟法估算精度并不高[11-12]。而集总式水文模型中部分参数仍然是经验方法，其中大多数依据需要通过观测到的降雨和径流数据反演获得。并且，集总式水文模型与实际降雨和径流过程不匹配，因此通常难以获得令人满意的结果[13]。

SWAT模型是搭建在地理信息系统(GIS)上的半分布式水文模型，可以用来模拟各种不同的水文过程[14]，模型组成部分主要包括气象、地表地下径流、蒸散发等[15]。该模型通过分析数字高程、土地利用类型、土壤类型以及水文气象数据建立主要的源汇特征，可以模拟流域内的径流变化特征。该模型已经被应用于大中小流域、干旱、半干旱地区，且都能够得到令人满意的模拟效果[16-19]。

本文的研究区域是位于青海德令哈县内的巴勒更河流域，首先研究水文模型能否适用于巴勒更河流域，然后利用该模型还原出流域1970—2015年的径流过程。最后从周期、趋势、突变等方面研究降雨-径流关系，并进一步探究气候因素和人类活动对该流域径流变化的贡献率。

2 研究区域概况

2.1 研究区域

巴勒更河流域位于青海海西内蒙古自治州德令哈盆地(图1)，位于96.6°E—96.83°E，37.33°N—37.6°N，海拔最高处为4 280 m，最低处为2 920 m。发源于宗务隆山巴勒更河，穿过怀头他拉灌区，最后注入克鲁克湖中，河流全长66.5 km。流域的集水面积882 km2，河道上下游比降1/66，多年年均流量0.75 m3/s，年径流总量0.237亿m3。该地区属于高原山地气候，多年平均气温4.2 ℃ ，相对湿度40%、多年平均风速2.3 m/s、多年平均降雨量181.8 mm，多年最小降水量120 mm，降雨主要集中在5—8月份，约占全年降水量的60%。怀头他拉水库位于巴勒更河流域出口处，修建于1959年，多年平均入库径流量0.6 m3/s，水库库容890万m3。

图1 巴勒更河流域Fig.1 Map of Balegen River basin

2.2 数据来源与处理

本次研究需要输入SWAT模型中的数据及其来源如表1所示，其中数字高程模型(DEM)和土地利用数据利用ArcGIS作投影变化、裁剪出所需研究区域；借助SPAW软件计算所需的土壤参数；气象数据来自德令哈、大柴旦、诺木洪3个气象站；太阳辐射利用气象站的日照数据进行计算[20]。

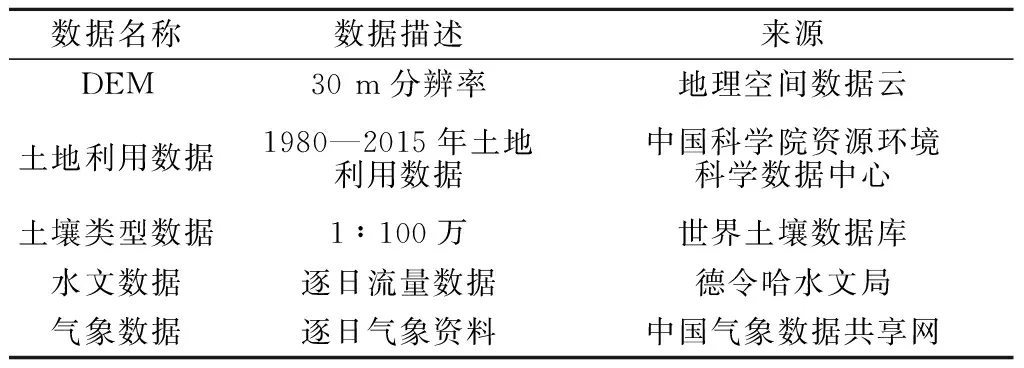
表1 原始数据说明Table 1 Description of original data

3 SWAT模型的降雨-径流模拟

3.1 SWAT模型原理

SWAT模型是Dile等[21]基于ArcGIS构建和开发的半分布式水文模型，模型将流域细分为子流域，再根据土壤类型、土地利用类型以及坡度将子流域细分为水文响应单元。模型需要输入包括土地利用类型(图2(a))、土壤类型(图2(b))、坡度、水文气象等数据。

图2 土地利用类型和土壤类型Fig.2 Land use patterns and soil types

模型的主要原理是水量平衡原理(式(1))，它综合考虑了流域内所有的水文过程[22]。

(1)

式中：QWt、QW0分别表示土壤最终状态和初始状态土壤含水量(mm)；t表示天数(d)；Pi表示某天的降雨量(mm)；Q表示地表径流深(mm)；ETi表示蒸散发量(mm)；Wi及QRi分别表示进入包气带的水量(mm)和回归流量(用深度表示，mm)；i表示某天。

(2)

式中：S为滞留系数(mm)；Ri为降雨深度(mm);Ia为降雨的初损(mm)。初损Ia与滞留系数S之间存在Ia=S，取值为0.2。当Ri>0.2S时径流出现，滞留系数S与土地利用、土壤类型、坡度有关，其关系式为

(3)

式中CN是与土壤类型、土地利用和土地管理条件相对应的SCS曲线编号。

3.2 参数敏感性分析与校准

为了提高模型校准的效率，本文使用SUFI-2算法的Global Sensitivity Analysis模块对流域出口处的23个参数进行敏感性分析，删除那些对模型模拟结果影响较弱的参数，最终得到12个有效参数，参数名称见表2。SUFI-2算法是将采用拉丁超立方随机采样方法取得的参数值[23]，代入模型进行模拟，计算得到目标函数值。使用t-stat和p-value指标值来评价参数是否足够敏感，当前者的绝对值越远离0时，则说明该参数在本次率定中对率定结果影响越显著；当p<0.05时表示该参数对结果的影响极为显著。敏感性分析结果见表2。

表2 SUFI-2算法敏感性分析结果Table 2 Sensitivity analysis results of SUFI-2 algorithm

利用SWAT模型的配套软件对模型进行参数率定，模型将2006—2008年3 a时间设置为模型预热期，2009—2013年作为模型参数校准期，2014—2015年作为模型参数的验证期。执行多组迭代，第一组迭代1 000次，其余每组迭代100次，每组迭代结束得到新的参数范围，使参数范围不断缩小，直至得到最优解。最优值见表2。

3.3 降雨-径流模拟方法与效果评价

通过使用纳什效率系数NSE、R2、PBIAS对模型模拟结果进行评价，详细计算公式如下：

(4)

(5)

(6)

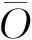
NSE一般用于验证模拟径流系列与实测系列的过程符合度，取值范围为[-∞，1]，值越靠近于1，表示模型模拟质量越好。R2表示模拟值与实测值的相关性，系数值越接近1，表明实测与模拟的相关性越高。PBIAS偏差百分比衡量模拟数据的平均趋势大于或小于观测值，最佳情况下为0，低幅度值表示模拟效果很好，值>0时表示模型被低估，值<0表示模型被高估[24]。当PBIAS<25%认为模型模拟结果是可信赖的； PBIAS<15%时认为模型能得到较好的模拟结果； PBIAS<10%时模型能够得到令人满意的结果。

3.4 参数校准与模型验证结果

对模型中12个主要参数先利用2009—2013年径流资料进行率定，然后再利用2014—2015年的资料进行验证，结果如图3所示。在校准期，模型径流模拟曲线与实测的径流曲线拟合效果较好；但在验证期，模型模拟的径流曲线与实测的径流曲线拟合效果较差。同时，从表3中模拟评价结果可知：校准期内R2和NSE均在0.76以上且PBIAS<3.8%，验证期R2和NSE分别只有0.58、0.51；但总体来说，模型模拟的月径流过程符合R2和NSE>0.5、相对误差<15%的要求，表明模型可以用于巴勒更河流域的径流还原[25]。

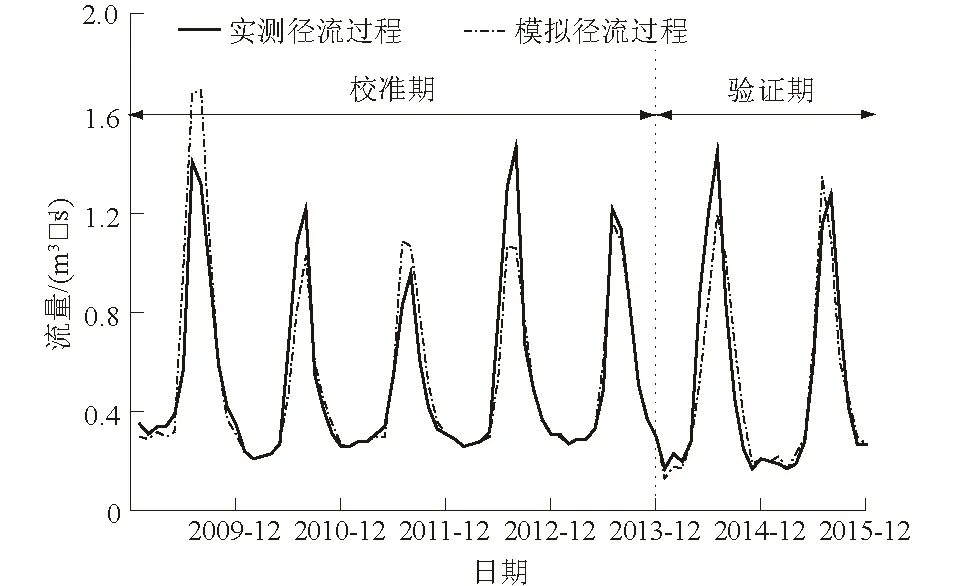
图3 实测与模拟径流过程Fig.3 Measured and simulated runoff process

表3 模拟评价结果Table 3 Simulation evaluation results

3.5 径流还原结果

将经过校准及验证后的12个参数返回到模型中，修改每个时期对应的土地利用类型(表4)，并驱动SWAT模型模拟相应时期的逐月径流过程，模拟结果如图4所示。

表4 不同土地利用类型年份对应径流还原时期Table 4 Runoff restoration periods corresponding toyears of different land use patterns

图4 径流量还原过程Fig.4 Runoff restoration process

4 降雨-径流关系及影响因素分析

为揭示巴勒更河流域降雨-径流关系随时的变化特征，研究其在时间上的演变机理，定量分析导致径流变化的影响因素具有重要意义。本文用Kendall秩次检验[26]和5点滑动平均[27]对流域降雨、径流趋势展开分析；利用Mann-Kendall(M-K)突变检验[28]识别降雨、径流的突变位置;用小波分析[29]识别降雨-径流的周期性;利用累积距平方法[30]判断降雨-径流关系的突变点。采用累积斜率变化率比较方法[31]定量分离出气候变化和人类活动对径流量变化的贡献率。

4.1 降雨、径流年际变化特征分析

巴勒更河流域1970—2015年降雨、径流变化过程及5点滑动平均如图5所示，降雨极大值发生在2009年，为307.39 mm，径流极大值发生在1986年，为0.27×108m3/s，极大值出现年份不统一，且偏离较大。降雨和径流出现极小值的时间大致相同，降雨极小值出现在1972年，径流发生在1971年,其值分别为66.73 mm和0.11×108m3。降雨、径流的趋势变化也不相同，其中降雨具有明显增加的趋势，而径流的变化趋势并不明显。由降雨、径流的滑动平均曲线同样可以明显看出，降雨、径流波动变化程度差别较大。同样地，降雨、径流发生突变的发生位置有差别，通过M-K检验得到降雨的突变位置发生在1981年、径流发生突变位置在1995年、2010年(图6)。从图7、图8中可以明显看出，降雨主要存在4、9、28 a的周期，其中以28 a的周期性变化最为显著。在这个周期段内，降雨经历“枯—丰—枯—丰—枯”5次丰枯交替，并且在未来的一段时间降雨仍然是偏枯的。径流主要存在4、10、23 a的周期，其中23 a的周期最为明显，在这个时期内径流经历了“枯—丰—枯—丰—枯”5次丰枯交替，同样地，在未来一段时间内，径流也将是偏枯，这与降雨的变化是一致的。

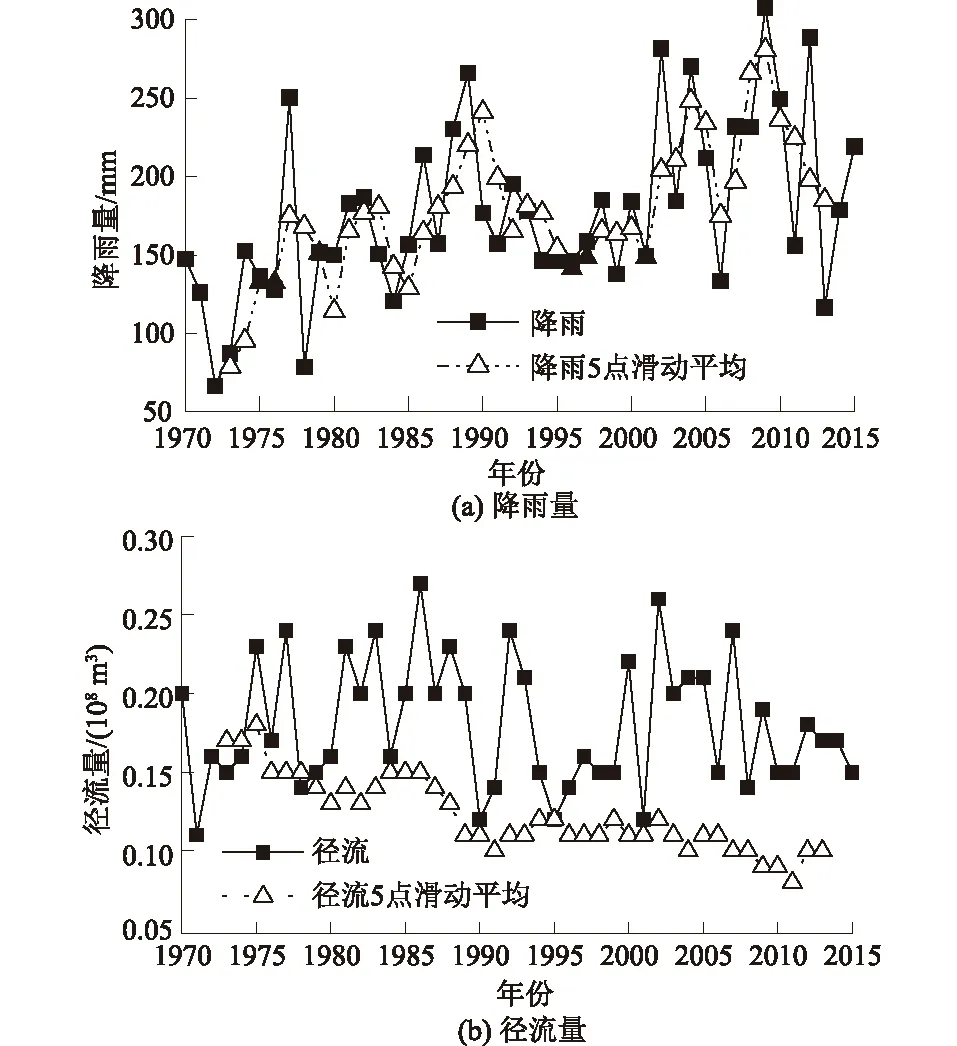
图5 降雨量和径流量随时间变化过程Fig.5 Time-history curves of rainfall and runoff

图6 降雨量和径流量的M-K检验Fig.6 M-K test of rainfall and runoff series

图7 小波分析系数实部等值线Fig.7 Wavelet coefficient real part of rainfall andrunoff series

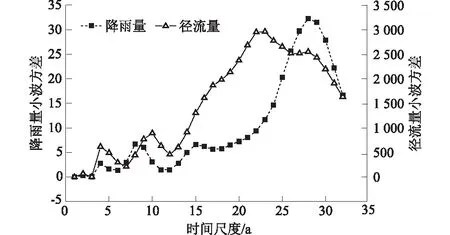
图8 降雨-径流小波方差Fig.8 Wavelet variance of rainfall and runoff series

4.2 降雨-径流关系变化分析

利用累积距平方法判断降雨-径流关系发生显著性改变的年份，并得到1970—2015年降雨累积距平年际变化(图9(a))，在1989年前后降雨累积距平分布表现出增大和减小的趋势，显然在该时段降雨发生突变。从1989—2015年降雨量累积距平的年际变化(图9(b))可以看出，在2001年前后降雨量累积距平曲线的变化趋势同样也是先减小后增大。

计算得到1970—2015年径流累积距平曲线，径流累积曲线在1989年(图9(c))、2001年(图9(d))前后都表现出不一样的趋势，这与同期降雨量累积距平的变化趋势是一样的。通过径流系数来进一步判断降雨-径流关系变化情况，首先采用5点滑动平均法分析径流系数变化趋势(图10)。从图10可知径流系数随着时间变化有明显的减小趋势。各个时期的径流系数均值能很好地表现出径流系数减少趋势。1989—2000年相较于1970—1988年，径流系数减少26.7%。推测径流系数减小的原因可能是德令哈地区在1988年撤镇建市，工业得到迅猛发展，城市取用水量明显增大。2001—2015年相较于1989—2000年，径流系数减少10%，这一时期相较于1989—2000年，径流减少更为显著，推测主要原因是在该时期怀头他拉撤乡建镇，城镇建立，该地区的需水量更大，河道内取水量增大。

图9 降雨、径流累积距平变化特征Fig.9 Changes in the cumulative anomalies ofrainfall and runoff series

图10 径流系数变化Fig.10 Change of runoff coefficient

4.3 径流变化对气候和人类活动的响应

气候、人类活动以及下垫面都是影响径流形成和变化的主要因素。本文利用累积斜率变化率比较方法计算影响研究区域径流变化因素的贡献率。此方法将气候因素简化为降雨，综合考虑人类活动的影响，并忽略了流域下垫面的影响[32]。

具体步骤为设累积降雨-年份线性关系式在拐点前后2个时期的斜率分别为SPa和SPb(mm)，累积径流量-年份线性关系的斜率在拐点前后2个时期的径流量为SRa和SRb(亿m3)，则累积降雨斜率变化率为(SPb-SPa)/SPa；同样地，累积径流斜率变化率为(SRb-SRa)/SRa，那么气候变化导致径流量变化的贡献率Cp(%)为

(7)

由此简化得到人类活动对径流变化的贡献率CH(%)，即

CH=100-Cp。

(8)

经过计算得到巴勒更河流域的累积降雨、径流斜率及其变化率如表5、表6所示。第1时期对应1970—1988年、第2时期对应1989—2000年、第3时期对应2001—2015年。第2时期与第1时期相比，累积降雨量-年份线性关系式的斜率减小了-8.72 mm/a，变化率为140.19%(表5)。与同期相比，累积径流-年份线性关系式的斜率减小了0.000 4亿m3/a，变化率为400%(表6)，利用式(7)、式(8)计算得到第2时期比第1时期的气候变化对径流量变化的贡献率为35%、人类活动影响的贡献率为65%(表7)。

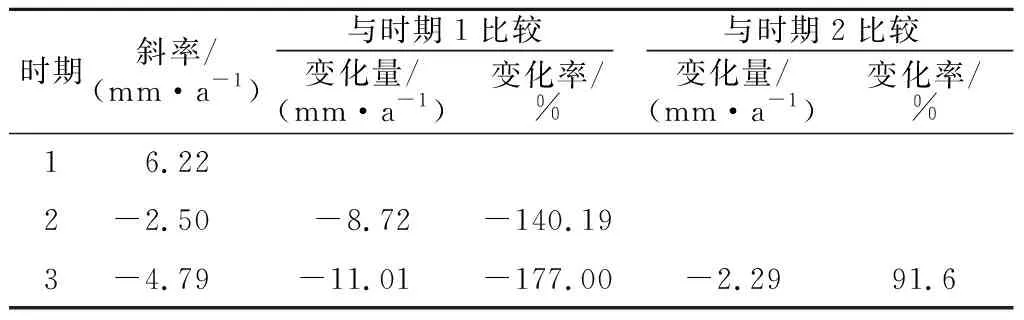
表5 累积降雨斜率及其变化率Table 5 Cumulative rainfall slope and its rate of change

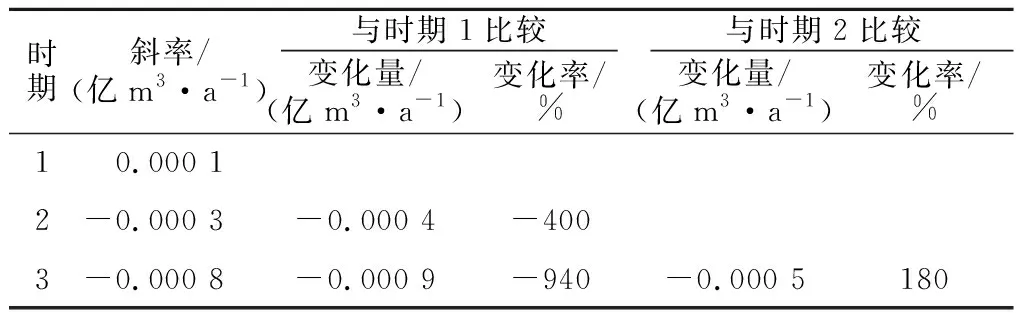
表6 累积径流斜率及其变化率Table 6 Cumulative runoff slope and its rate of change

表7 气候变化和人类活动对降雨、径流贡献率Table 7 Contribution rates of climate change andhuman activities to rainfall and runoff

第3时期与第2时期相比，累积降雨-年份关系式的斜率减小-2.29 mm/a，变化率为91.6%(表5)。同期相比累积径流-年份关系式的斜率减少-0.000 5亿m3/a，变化率为180%(表6)。计算得到第3时期相对于第2时期气候变化和人类活动对径流变化的贡献率分别为51%、49%(表7)。

5 结论与讨论

利用SWAT模型还原巴勒更河流域46 a径流过程，并分析其降雨-径流关系的变化及原因，结论如下。

(1) 将SWAT模型应用于巴勒更河流域，参数校准期(2009—2013年)的评价指标R2=0.78、NSE=0.76，说明模型在校准期模拟效果较好。在验证期(2014 — 2015年)R2=0.58、NSE=0.50，模型结果可信。进而可利用模型还原1970—2008年的径流数据。

(2)从趋势、突变、周期以及相关关系角度分析巴勒更河的降雨序列和经过SWAT模型延长以后的径流序列，降雨具有显著的上升趋势，而径流的上升趋势不显著；降雨-径流的突变点上也存在差异，降雨突变发生在1981年，而径流在1995年、2010年都发生突变；两者周期性上存在着相同的周期，但主周期不同，降雨主周期为23 a，径流则为28 a。通过降雨量、径流量累积距平曲线可以看出，降雨量与径流量在1989年和2001年降雨-径流的关系发生两次显著性变化，变化前后径流系数分别减小26.7%、10%。

(3)以1970—1988年为基准期，1989—2000年降雨变化和人类活动的相对贡献率为35%和65%，在2001—2015年的相对贡献率为19%和81%。以1989—2000年为基准期，2001—2005年降雨量和人类活动对径流量的影响贡献率分别为51%、49%。

(4)降雨-径流关系在1989年、2001年发生了明显的改变，主要是因为在1988年德令哈建市、2001年怀头他拉撤乡建镇都导致人类活动增强从而影响径流变化。