A classical relativistic hydrodynamical model for strong EM wave-spin plasma interaction

Qianglin HU (胡强林) and Wen HU (胡文)

Department of Physics, Jinggangshan University, Ji’an 343009, People’s Republic of China

Abstract Based on the covariant Lagrangian function and Euler–Lagrange equation,a set of classical fluid equations for strong EM wave-spin plasma interaction is derived.Analysis shows that the relativistic effects may affect the interaction processes by three factors:the relativistic factor,the time component of four-spin,and the velocity-field coupling.This set of equations can be used to discuss the collective spin effects of relativistic electrons in classical regime, such as astrophysics, high-energy laser-plasma systems and so on.As an example, the spin induced ponderomotive force in the interaction of strong EM wave and magnetized plasma is investigated.Results show that the time component of four-spin, which approaches to zero in nonrelativistic situations, can increase the spin-ponderomotive force obviously in relativistic situation.

Keywords: Lagrangian function, strong EM wave, spin plasma, spin ponderomotive force

1.Introduction

In the last two decades,the spin effect in plasma has attracted a lot of attentions because of its potential applications[1–3].Spin effect is an important property of quantum plasma, and researches have shown that it may exist even on a classic scale,which is longer than the thermal de Broglie wavelength[4].Researches have also shown that under certain conditions, the spin contributions can be more important than the usual quantum plasma corrections[5].In the nonlinear situation,the spin force appears to be more importance and cannot be ignored even in moderatedensity high-temperature plasma, due to the fact that the electrons with different spin eigenstates can be separated by the spin induced ponderomotive force [6].

Some models have been developed to study the spin plasma.In nonrelativistic regime, a fluid theory is developed from the Pauli Hamiltonian and Madelung decomposition of electron wave function [5, 7].Based on this fluid theory, some new phenomena, such as new propagation modes [8], magnetosonic solitons[9],instabilities[10],and so on,are revealed.In relativistic regime [11–16], the EM wave-spin plasma interactions have been considered on three levels: classical physics, relativistic quantum mechanics, and quantum field theory.On classical physics level,a classical relativistic model is developed directly from the Bargmann–Michel–Telegdi equation.However, in this model the spin does not affect the electron dynamics[17].On relativistic quantum mechanics level,using the Foldy–Wouthuysen ransformation of Hamiltonian for positive energy states of electron, a phase-space scalar kinetic model based on the gauge-invariant Stratonovich–Wigner function [18] and a fluid model based on the Madelung decomposition of electron wave function with two spinor [19]are developed for weakly relativistic spin plasma.On quantum field theory level, a set of fully covariant hydrodynamic equations are obtained based on Dirac theory of electrons [20].However, the covariant model is very complex and is rather difficult to implement in practical situations, especially for numerical applications [19].

In addition to these, there are some other works on spin plasma [21–23].In the present work, we developed a classical hydrodynamical model for relativistic spin plasma based on the covariant Lagrangian function and Euler–Lagrange equation.The equations of this model are formally consistent with the equations of the model proposed in[20].However,this model is mathematically much simpler and is easy to implement in practical situations.Admittedly, as a classical model, some quantum plasma corrections, such as quantum statistic effects and quantum diffraction effects, are not included in this model.Therefore, this model can be applied to discuss the spin effects of strong relativistic plasma in classical regime, such as in astrophysics, high-energy laser-plasma systems and so on.Analysis shows that the relativistic effects may affect the physical processes by three factors: the relativistic factor, the time component of four-spin, and the velocity-field coupling.

In the end, this model is used to examine the spin contribution to the ponderomotive force of strong EM wave interacting with magnetized plasma, which has been discussed by some authors [6, 24, 25] in nonrelativistic regime.Results show that the time component of four-spin,which approaches to zero in nonrelativistic situations, can increase the spin-ponderomotive force obviously in relativistic situation.

2.Basic equations

The Lagrangian function of electron in electromagnetic(EM)field can be written as

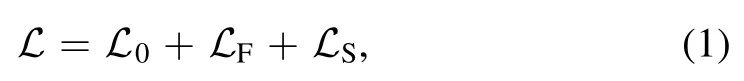
whereL0= -mc2/is the Lagrangian function of free electron,m,c,are the rest mass of electron, the light speed in vacuum and the relativistic factor of electron,respectively,is the ordinary electron-EM field interaction Lagrangian [26],eis the electric quantity of an electron,uαis the 4-velocity of electron andAαis the 4-vector potential,LS=σμ(-α Fμν σν)is the spin-EM field interaction Lagrangian[27],α=e/mc,and the Landé factorg=2 is presumed,σμis the 4-vector spin,andFμνis Maxwell electromagnetic field tensor.The ions are viewed as a uniformly positive back-ground.

To obtain the motion equation from equation(1),we use Lagrange equations

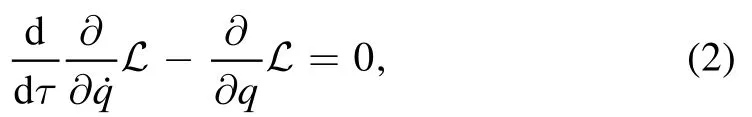
whereτis the proper time, andqis the generalized coordinates.From equations (1) and (2), we obtain

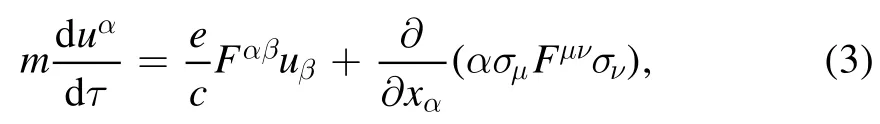
and

Equations(3)and(4)are the motion equations of single electron.Consideringequations (3) and(4) can be rewritten as

and

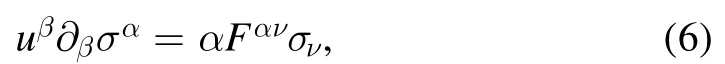
where∂β≡ (∂ /c∂t,∂/∂xi)is the 4-gradient operator.

Assuming that the electron distribution function isf(x,p,σ),the fluid densitynin the rest frame of fluid can be written as

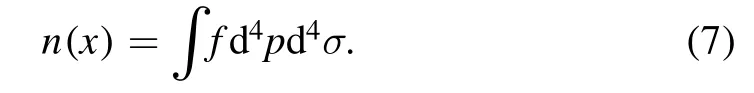
The statistical average of any physical quantityRμis defined as

Therefore, the fluid four-velocity isUμ= 〈uμ〉and the fourspin density isSμ= 〈σμ〉.The microscopic four dimensional velocity and spin density in the rest frame are also defined asvμ=uμ-UμandΣμ=σμ-Sμ,respectively.It is easy to obtain that〈vμ〉 = 0= 〈Σμ〉.

Taking the ensemble average of equations(5)and(6),we obtain

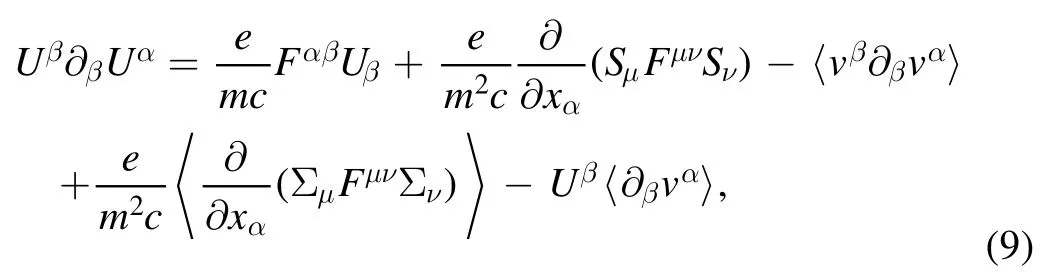
and

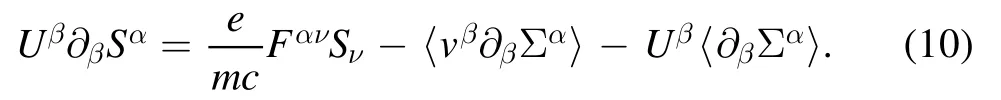
Moreover, if the creation of electron pairs can be neglected,the conservation of electron number gives

Equations (9)–(11), plus the macroscopic Maxwell equations

form a complete and covariant description of relativistic spin plasma.

3.Vectorial description

It is useful to put equations (9)–(11) into the general threedimensional vector forms.To do this, we use the usual procedure [20] and rewrite the four-velocity of fluid as

whereUis the spatial component of the fluid velocity,fγis the average relativistic factor.Considering the constraintuμ uμ=c2and the definition ofvμ,it is easy to obtain

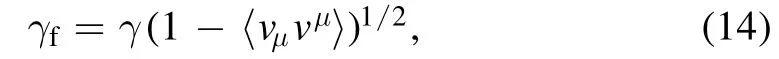
whereγ= (1-U2/c2)-1/2.The macroscopic four-spin density is

Considering the covariant constraintUμ S μ=0,the time component can be obtained asS0=(1/c)U·S.

Therefore, equation (9) can be written in the vectorial form

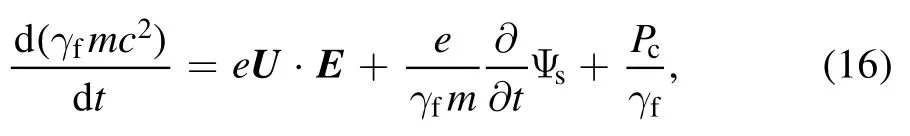
and

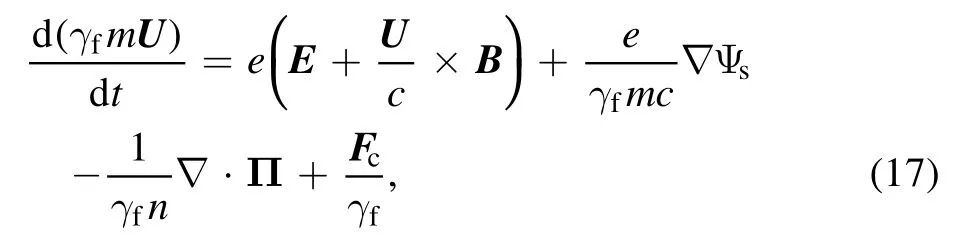
where

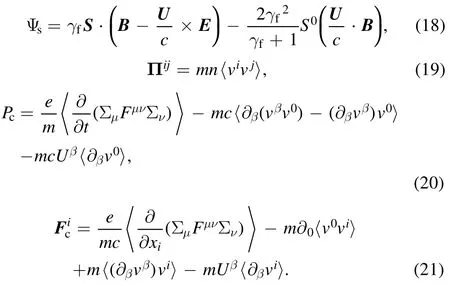
Equations (16) and (17) are the time and special components of equation (9), respectively.sΨ is the spin potential(the derivation is shown in appendix), and in the nonrelativistic limit, it is equivalent to the corresponding item in [5].Π is the pressure tensor.PcandFcare the nonlinear corrections of the power and force caused by the microscopic four dimensional velocity and spin density in the rest frame of fluid.

Equation (10) can be written as

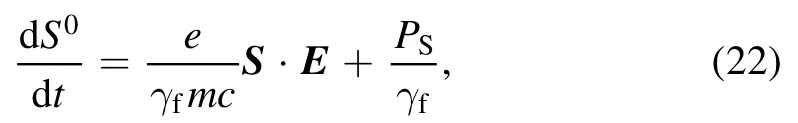
and

where

Equations (22) and (23) are the time and special components of equation (10), respectively.K is the coupling tensor of thermal-spin.PSandSΞare the nonlinear corrections to the spin evolution caused by the microscopic four dimensional velocity and spin density in the rest frame of fluid.

The continuity equation (11) becomes

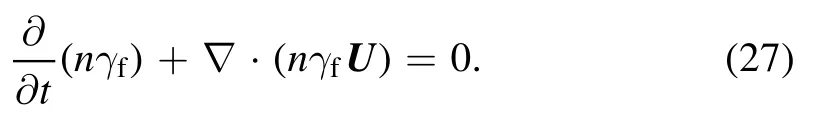
Equations(16),(17),(22),(23),and(27)form a full set of macroscopic hydrodynamical equations.Comparing with the nonrelativistic limit results, it is easy to know that the relativistic effects mainly affect the interaction processes by three factors: firstly, the relativistic factorγf;secondly, the time component of four-spinS0, as shown in equations (18) and (23); and lastly, the velocity-field coupling, as shown in equation (18).This set of equations can be used to discuss the spin effects of relativistic plasma,which exist widely in astrophysics, high-energy laserplasma systems and so on.

4.Spin-ponderomotive force

As an example, we will illustrate how the time component of four-spinS0affects the EM wave-spin plasma interaction process in the following part.In order to do this, we apply the formalism developed in the present work to discuss the spin induced ponderomotive force in magnetized plasma, which has been studied by some authors[6, 24, 25] in nonrelativistic regime.Take the assumption that the back-ground magnetic field isB0=.The electrons have two eigenstates, i.e.spin-up and -down relative toB0.Though the spin states of electrons can be disturbed by the EM waves, the differentiation of spin-up and -down electrons is still well defined provided the physics associated with spin flips can be neglected [4, 6].Therefore, the electrons are treated as two kinds of populations in the present work,and equations(17)and(23)are reduced to

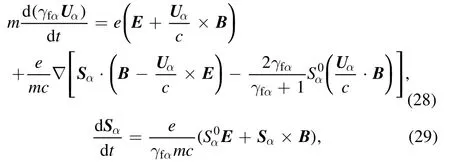
in the cold plasma,where the subscriptα= ↑or ↓,denotes spin-up or spin-down.In the nonrelativistic limit, i.e.∣Uα∣≪c,equations (28) and (29) reduced to the equations which have been used in [6].

In the present work, the derivation of the spin-ponderomotive force is also based on the perturbative analysis [6].In the following part,we assume a slowly varying plane circularly polarized EM waveE=(1 /2)exp [i (kz-ωt)]+c.c.,where c.c.denotes complex conjugate, and defnie the variablesE±=Ex±iEy,U±=Ux±iUy,S±=Sx±iSy.Separating the EM wave magnetic feild and the back-ground magnetic feild by lettingB=B0+B,and writingSαintoSα=Sα0+Sα,the 1ω-frequency component of equation(29)can be written as

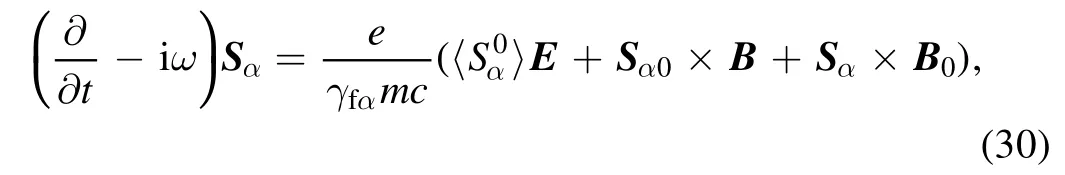
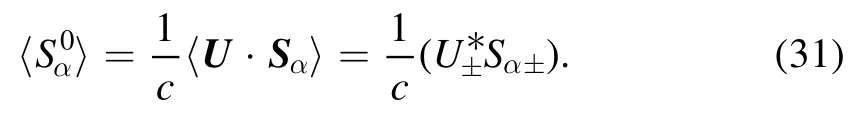
The lowest order ofUαcan be obtained from equation (28) as

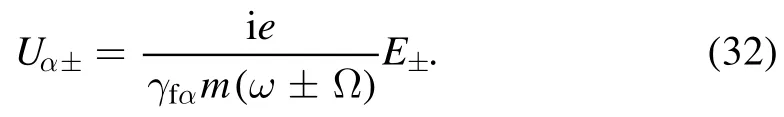
Equation (32) shows that in the lowest order of approximation,the velocity of electron is not influenced by the spin, and from now on,the subscriptαinUαandfγαwill be dropped.Thus,the lowest order ofSαcan be obtained from equation (30) as

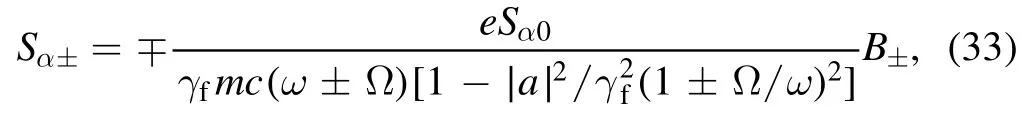
whereΩ =∣e∣B0/(γfmc)is the cyclotron frequency, and∣a∣ =∣eE∣ /(mω c)is the normalized potential of EM wave.Usingγ2f= 1+∣a∣2/(1± Ω/ω)2,equation (33) reduced to

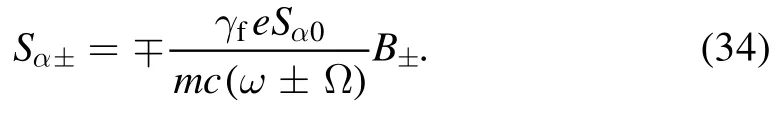
Therefore, substituting equation (34) into the correction term of equation (30) gives

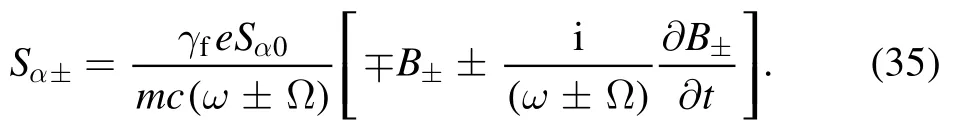
The spin induced ponderomotive force can be written as [6]

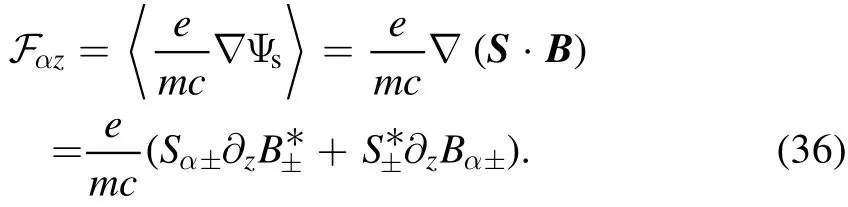
Substitution of equations (34)and(35)into equation(36)gives

It is easy to verify that in the nonrelativistic limit,equation(37)is the same with the result in[6].Equation(37)shows that in the relativistic situation, the spin-ponderomotive force increased with the relativistic factor, i.e.increased with the EM wave intensity.Lettingξ=z-vgt,equation(37)can be transformed to the commoving frame

The ratio of the spin-ponderomotive force in relativistic and nonrelativistic situation is

whereFα zis the spin-ponderomotive force for nonrelativistic situation,i.e.Equation(13)in[6].Generally,the ponderomotive force is decreased with the increase of the effective mass of the particle.Equation (39) implies that in relativistic situation, in spite of the electron effective mass is increased, the spin-ponderomotive force isfγtimes larger than the spin-ponderomotive force in nonrelativistic situation due to the influence of the time component of four-spin.Figure 1 shows the variation ofRversusafor left-hand and right-hand circularly polarized(LCP,RCP)waves,where the EM wave lengthλ=1.06μm and the back-ground magnetic feildB0=1000 Tare presumed.Figure 1 obviously shows thatRincreased with the increase ofa.Researches[6]have shown that in the EM wave-spin plasma interaction,the spin-ponderomotive force can separates the spinup and spin-down electrons.The reason is that the spin-ponderomotive forces acting on the two species of electrons are in opposite direction [6, 24].Equation (39) means that in the relativistic situation, the time component of four-spin can increase the degree of the separation of these two kinds of electrons.

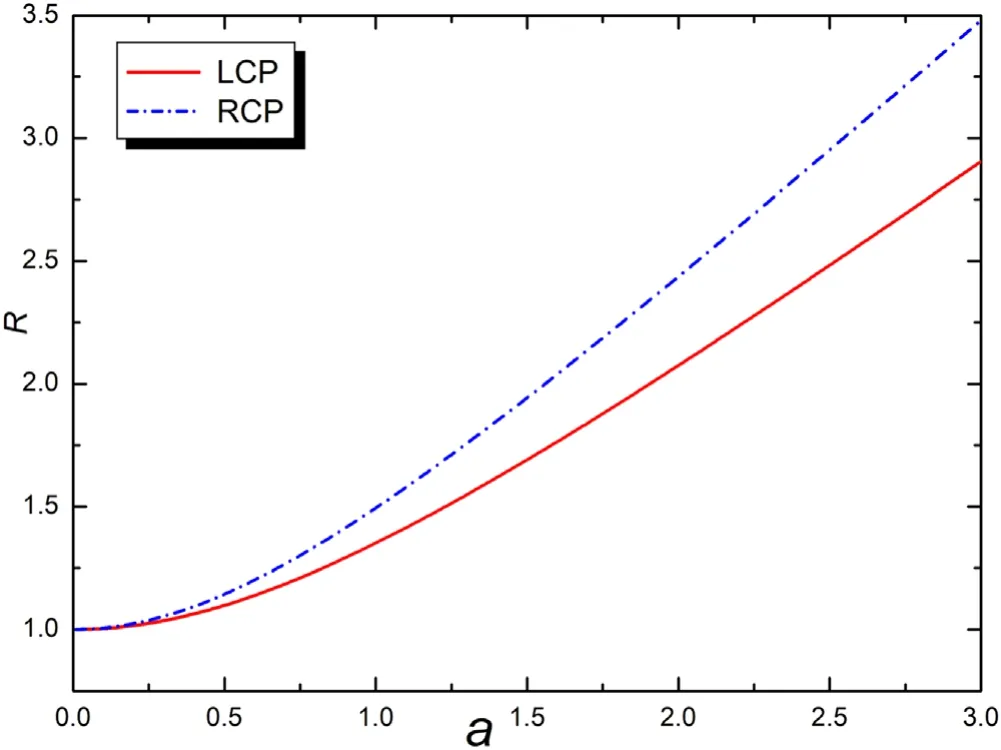
Figure 1.The variation of R versus a.EM wave length λ=1.06 μm,B0 =1000 T.

5.Conclusion

Spin effect is an important property of quantum plasma and several models have been proposed on it.In this work, we developed a classical hydrodynamical model for relativistic spin plasma based on the covariant Lagrangian function of electrons.This model can be used to discuss the spin effects of strong relativistic plasma.Analysis shows that the relativistic effects may affect the interaction processes through three aspects:fristly,the relativistic factorγf;secondly,the time component of four-spinS0; and lastly,the velocity-field coupling.However,it needs further research to know what phenomenon can be triggered by these factors.

The present model is different from the previous models[5, 7, 17–20].(1) The present model can be used for strong relativistic cases.The existing models developed from quantum mechanics are mainly applied to non-relativistic[5, 7] or weakly relativistic [18, 19] cases.(2) The present model is mathematically simple and is easy to implement in practical situations.Though the model developed from quantum field theory[20]is a covariant model and includes as many quantum effects as possible, it is very complex and is rather difficult to implement in practical situations,especially for numerical applications [19].(3) The present model naturally includes the main spin effects.The model proposed in[17]is also a relativistic model,but some crucial spin effects,such as the spin potential, thermal-spin coupling, and so on,are ignored.However,the equations of the present model are formally consistent with the model proposed in [20].Admittedly,as a classical model,some quantum effects,such as quantum statistic effects and quantum diffraction effects,are not included in the present model.Therefore, it is applicable for the conditions that the plasma temperature is much higher than the Fermi temperature and the force induced by Bohm potential is much smaller than the spin force.Actually, these conditions are satisfied in numerous cases such as astrophysics, high-energy laser-plasma systems and so on.

The model has been applied to examine the spin contribution to the ponderomotive force of strong EM wave interacting with magnetized plasma in this work.Results show that the time component of the four-spin can increase the spin-ponderomotive force obviously in relativistic situation.

Acknowledgments

This work was supported by National Natural Science Foundation of China (No.12065011), and Science and Technology Research Project of Jiangxi Provincial Department of Education (No.GJJ170642).

Appendix.The derivation of Ψs

Considering thatSμ F μν Sνfulfills the requirements of covariance, we have

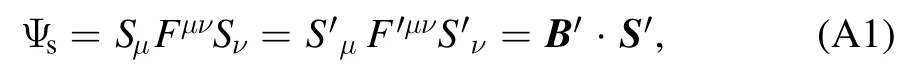
where the quantities with prime denote the quantities in the electron rest frame andS′0=0.In the last equality, the commutation relation[S′i,S′j]=∈ijk S′kis used.Using the general Lorentz transformation, one can obtain [26]

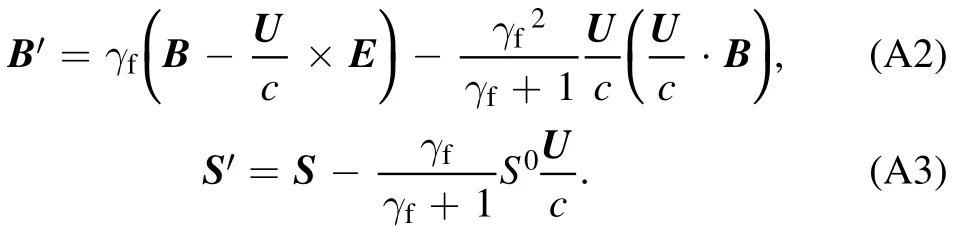
Therefore,

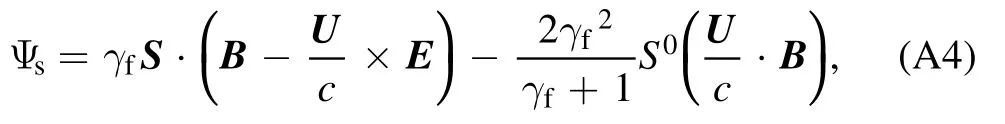
where the term including(U/c)3is neglected.