开普勒行星运动定律的理解
2022-04-15■胡明
■胡 明
德国著名天文学家、物理学家开普勒经过20 余年的潜心研究发现了一系列关于行星的运动规律,并将其总结为三条基本规律分别于1609年和1619年发表在《新天文学》和《宇宙和谐论》中,这就是我们现在所熟知的开普勒行星运动定律。
一、开普勒第一定律
1.内容:所有行星绕太阳运行的轨道都是椭圆,太阳处在椭圆的一个焦点上。
2.理解:开普勒第一定律指出了行星绕太阳的运行轨迹是椭圆,而不是圆,因而行星与太阳之间的距离时刻在变化,行星运行速度的大小和方向都在不断改变。不同行星绕太阳运行时的椭圆轨道是不同的,但太阳处在所有这些椭圆的一个焦点上。
例1 下列关于开普勒第一定律的说法中正确的是( )。
A.太阳系中的所有行星都有一个共同的轨道焦点
B.行星的运动方向总是沿着轨道的切线方向
C.行星的运动方向总是与它和太阳的连线垂直
D.火星绕太阳沿椭圆轨道运行时,其线速度大小保持不变
根据开普勒第一定律可知,太阳系中的所有行星都围绕着太阳沿不同的椭圆轨道运行,太阳位于这些椭圆轨道的一个焦点上,选项A 正确。行星的运动方向总是沿着椭圆轨道的切线方向,选项B正确。当行星从近日点向远日点运动时,行星的运动方向与它和太阳连线的夹角大于90°,当行星从远日点向近日点运动时,行星的运动方向与它和太阳连线的夹角小于90°,选项C错误。火星绕太阳沿椭圆轨道运行时,其线速度大小和方向都在时刻变化,选项D 错误。
答案:AB
二、开普勒第二定律
1.内容:任意一个行星与太阳的连线在相等的时间内扫过的面积都相等。
2.理解:开普勒第二定律给出了行星绕太阳公转时面积与时间的关系,根据开普勒第二定律可以推导出行星在近日点的线速度大于在远日点的线速度,在近日点的角速度大于在远日点的角速度,在近日点的加速度大于在远日点的加速度。
例2 根据天文观测,土星绕太阳运行的轨迹如图1 所示,当土星沿其椭圆轨道从A点向B点运动时,下列关于土星的线速度v,加速度a,角速度ω的关系式中正确的是( )。
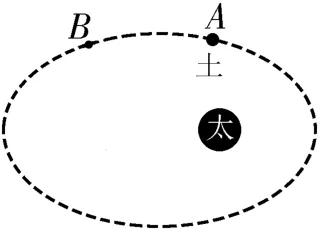
图1
A.vA>vB,aA>aB,ωA>ωB
B.vA>vB,aA<aB,ωA>ωB
C.vA<vB,aA<aB,ωA<ωB
D.vA>vB,aA<aB,ωA<ωB
当土星沿其椭圆轨道从A点向B点运动时,即从近日点向远日点运动,根据开普勒第二定律可知,其线速度、加速度和角速度均逐渐减小,即vA>vB,aA>aB,ωA>ωB。
答案:A
三、开普勒第三定律

3.拓展:开普勒第三定律不仅适用于行星绕太阳的椭圆运动,也适用于任意天体绕中心天体的椭圆运动,以及近似处理时任意天体绕中心天体的圆周运动。中心天体不同,则比值k也不同,即比值k是一个只与中心天体有关的常量。
例3 如图2所示,“嫦娥五号”返回器在半径为R的圆形轨道上绕地球稳定运行,其周期为T。当“嫦娥五号”返回器获得月壤样品,需要将样品带回地球时,可在其运行轨道上某一点A,将速率减小到适当数值,从而沿着以地心为焦点的椭圆轨道运行(椭圆轨道与地球表面相切于B点)。设地球半径为r,则“嫦娥五号”返回器从A点返回到地面B点所需的时间为( )。

图2


