平面向量问题中的求解策略
2022-04-15刘大鸣特级教师
中学生数理化·高一版 2022年3期
■杨 立 刘大鸣(特级教师)
高考对平面向量仍将以向量的线性运算,向量的夹角以及最值问题进行重点考查,凸显数形结合思想、转化与化归思想的具体应用。
策略1:利用平面向量基本定理化归几何问题

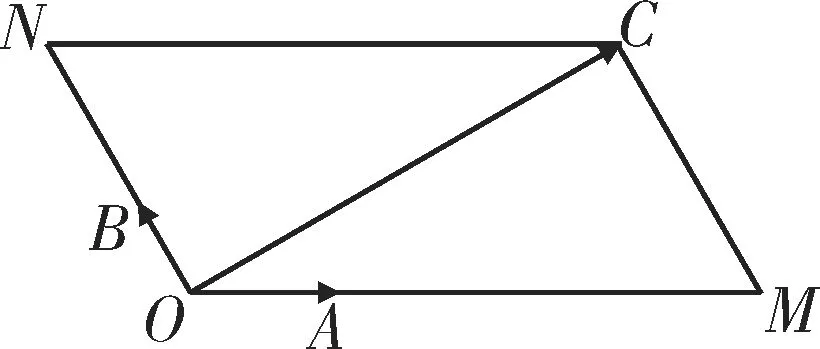
图1

评注:用平面向量基本定理解题的一般思路:先选择一组基底,并将条件和结论中的向量用该基底表示,再通过基底向量的运算来解决。
策略2:利用模的平方将向量问题实数化


评注:|a|2=a2=a·a可以实现由数的运算到向量的运算的转化,因此遇到向量的模就要有先平方的意识。
策略3:利用数量积运算求向量的夹角

评注:解答本题的关键是要熟记两个向量夹角的取值范围是[0,π]。
策略4:利用数量积的最值合理转化为函数的最值
例4 如图2,半圆的直径AB=6,O为圆心,C为半圆上不同于A,B的任一

图2


评注:由于数量积为实数,因此可以将数量积的最值转化为函数的最值求解。
