平面向量的应用与余弦定理、正弦定理综合演练
2022-04-15刘中亮
■刘中亮
一、选择题
1.已知作用在点A的三个力f1=(3,4),f2=(2,-5),f3=(3,1),且A(1,1),则合力f=f1+f2+f3的终点坐标为( )。
A.(9,1) B.(1,9)
C.(9,0) D.(0,9)
2.不解三角形,则下列说法中正确的是( )。
A.a=7,b=14,A=30°,有两解
B.a=30,b=25,A=150°,有一解
C.a=6,b=9,A=45°,有两解
D.a=9,b=10,A=60°,无解
3.(多选题)在△ABC中,角A,B,C的对边分别为a,b,c,则下列结论中正确的是( )。
A.若acosA=bcosB,则△ABC一定是等腰三角形
B.若cosA>cosB,则sinA<sinB
C.若△ABC是锐角三角形,则sinA+sinB+sinC>cosA+cosB+cosC
D.若△ABC是钝角三角形,则tanA·tanB+tanBtanC+tanCtanA<3
4.(多选题)对于△ABC,有如下命题,其中正确的命题是( )。
A.若sin2A=sin2B,则△ABC是等腰三角形
B.若△ABC是锐角三角形,则不等式sinA>cosB恒成立
C.若sin2A+sin2B+cos2C<1,则△ABC为钝角三角形

5.(多选题)在△ABC中,角A,B,C的对边分别是a,b,c,若a= 10,a2+b2-c2=absinC,acosB+bsinA=c,则下列结论正确的是( )。
A.tanC=2

三、解答题
10.如图1,已知AD,BE,CF是△ABC的三条高,且交于点O,DG⊥BE于G,DH⊥CF于H。证明:HG//EF。
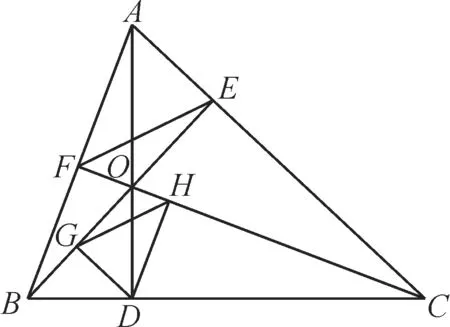
图1
11.如图2所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE。
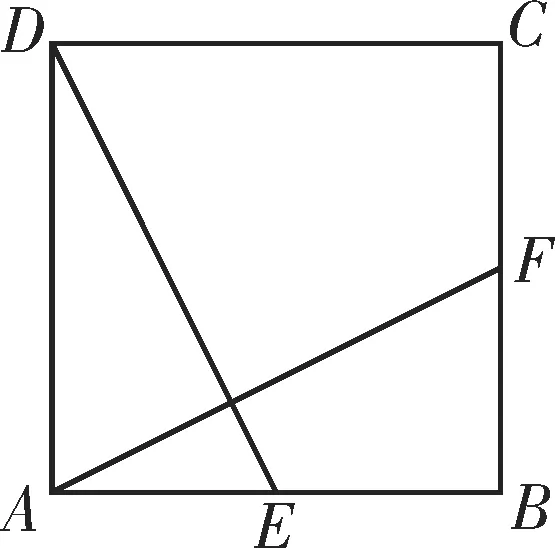
图2
12.在①ac= 3,②csinA=3,③c= 3b这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c的值;若问题中的三角形不存在,请说明理由。






