认知工业物联网中基于麻雀搜索算法的频谱分配策略
2022-04-14尹德鑫张达敏张琳娜蔡朋宸秦维娜
尹德鑫,张达敏,张琳娜,蔡朋宸,秦维娜
(1.贵州大学大数据与信息工程学院,贵阳 550025;2.贵州大学机械工程学院,贵阳 550025)
引言
工业物联网(Industrial internet of things ,IIOT)是工业领域的物联网技术[1-2],它将采集到的数据通过网络传输或处理,并不断将其集成到工业生产过程的各个环节的技术中去,实现工业智能化[3]。工业物联网需要用到无线通信技术,相对传统物联网,接入工业物联网的工业设备种类和数量众多,系统需要处理的数据量迅速增长,因此会对计算资源和通信资源导致一定的压力[4]。无线资源的分配往往决定着通信系统的吞吐量、能效以及频谱效率等关键性能。因此,有限的无线资源限制了工业物联网发展,而认知无线电(Cognitive radio,CR)的出现有效地改善了这一问题[5]。
认知工业物联网(Cognitive industrial internet of things,CIIOT)是将IIOT 与CR 相结合,通过利用一些许可频谱来扩展可用频谱资源,例如无线电/电视频谱、4G/5G 频谱和其他工业频谱,因此,CIIOT可以很好地适应大量工业数据的处理和传输,但是目前关于CIIOT 的研究还很少[6-7]。
为了最大限度地提高能量效率,文献[8]提出一种基于无线能量收集的CIIOT,以获取主用户信号的射频能量,并在不同频谱接入方式下提出资源分配策略,最大化CIIOT 的平均传输速率,并保证其节能要求;文献[9]提出了一种在认知无线电传感器网络用于能量收集的分布式传输功率控制策略,根据网络情况动态调整节点的传输功率,以维系网络连接性,这种动态传输功率调节可转换网络逻辑拓扑,以更好地适应网络的功率状况。
为了最大限度地提高频谱效率,文献[10]提出了一种优化认知物联网(Cognitive internet of things,CIOT)能量和频谱效率方案,其中每个节点可以机会性地访问空闲频谱并从周围的射频源获取能量;文献[11]提出了一种在空闲频段和非空闲频段中运行的,使用认知无线电的低功耗广域网的物联网动态频谱接入技术,主要目的是在不干扰许可低功耗广域网(Low power wide area network,LPWAN)主要用户的情况下,最大化认知用户的频谱容量。
为了提高物联网用户的公平性,文献[12]在工业物联网中提出一种联合非正交多址和时分多址(Non-orthogonal multiple access-time division multiple access,NOMA-TDMA)的资源分配方案,通过非正交多址(Non-orthogonal multiple access,NOMA)实现多个传感器在同一时频资源块内传输,共同优化了用户调度、时隙分配和功率控制,以使系统最大化在发射功率约束和最小速率约束下的公平效用。
综上所述,文献[8]虽将认知无线电与工业物联网结合来解决IIOT 资源分配问题,但没有考虑频谱优化问题,文献[9-12]主要考虑优化频谱分配和功率控制,但未对提出的资源分配算法进行优化,致使最终获取的不是最佳资源分配方案。基于此,本文引入认知工业物联网的概念来优化用户的能量效率和公平性,解决工业物联网中的频谱分配和干扰问题,提出一种联合改进二进制麻雀搜索算法(Improved binary sparrow search algorithm,IBSSA)和改进闭环功率控制算法的频谱分配方案,首先采用改进二进制麻雀搜索算法为CIIOT 用户分配频谱资源,然后采用改进闭环功率控制算法来降低用户间产生的干扰。仿真结果表明,改进后的策略优化了认知工业物联网中的频谱资源,明显提高了工业物联网的公平性和能量效率。
1 系统模型
随着工业数据的快速增长,工业物联网正在进入大数据时代,大数据时代需要更大的带宽来传输海量数据[13],因此,未来的网络必须满足工业物联网的各种需求,例如频谱、功率和成本。由于预计将要连接大量设备,频谱稀缺是一个会影响服务质量(Quality-of-service ,QoS)的约束。CIIOT 是将认知无线电与工业物联网结合,在主用户(PU)通信不被干扰的条件下,通过访问PU 的频谱来扩展可用频谱资源,提升频谱利用率。由于CR 的机会频谱接入可能会给PU 带来一定程度的干扰并降低QoS,因此对功率控制进行优化,降低对PU 的干扰并同时确保为所有用户提供最佳的QoS。
本文结合CIIOT 的概念,构建一种新的认知工业物联网模型。IIOT 中的工业设备可以被作为是认知无线网络中的用户,通过在IIOT 中融合认知无线电技术,实现主次工业物联网设备共享频谱资源,大大提升频谱资源利用率。系统模型如图1 所示,假设在工厂环境中,存在随机分布的N个认知用户(SU),M个主用户(PU)空闲的信道,分别用ρ={1,2,…,N}和κ={1,2,…,M}表示,主基站(PBS)和认知基站(CBS)都有各自的覆盖范围,在所属范围内用户使用自己分配到的信道和所属基站通信,CBS 可供N个SU 服务,PBS 可供K个PU 服务,当检测到可用频带时,将数据发送到数据中心,再由数据中心进行分配。

图1 认知工业物联网系统模型Fig.1 CIIOT system model
在工厂环境中,假设在SU 和PBS 之间没有信道增益,但是PU 和CBS 之间有信道增益,SU 和CBS之间也存在信道增益,信道增益与用户距CBS 的路径距离有关,信道增益可以表示为

式中:dn表示认知用户n到CBS 的距离,d0为参考距离,λ为发射频率波长,γ为路径损耗指数,Xg为阴影参数。根据以上内容定义系统模型主要组成部分如下
(1)可用矩阵:U={un,m|un,m∈{0,1}}N×M,U为一个N×M二维矩阵,un,m为认知用户n对信道m的使用状况,un,m=0 表示SUn不能使用信道m,un,m=1,则表示SUn可以使用信道m。
(2)效益矩阵:E={en,m|en,m>0}N×M,E为一个N×M的实数矩阵,矩阵内各个元素表示CIIOT 用户n在信道上获取的效益,en,m通常用带宽或吞吐量表示,根据香农定理,可以表示为

式中w为信道m的带宽。
(3)干扰矩阵:当PBS 和CBS 覆盖范围有交叉重叠时,使用相同信道产生的信道干扰值Gn,m构成在频段范围内的干扰矩阵G={gn,k,m|gn,k,m∈{0,1}}N×N×M,G为M个N×N二维矩阵构成的三维矩阵,gn,k,m=0 表示认知用户n和主用户k同时使用信道m不会产生干扰,gn,k,m=1 则表示会产生干扰。
(4)无干扰分配矩阵:X={xn,m|xn,m∈{0,1}}N×M,X为一个N×M二维矩阵,xn,m=1 表示信道m可以被认知用户n占用。要想SU 占用的信道对其他用户不造成影响,无干扰分配矩阵必须满足无干扰分配条件gn,k,m=1,xn,m×xn,m=0,∀0≤n,k≤N,0≤m≤M。
(5)用户效益值:若在确定无干扰分配矩阵X情况下,用户n的效益rn为

式中:i表示第i个次用户,N为最大次用户数,ei为第i个次用户使用的带宽。
2 改进二进制麻雀搜索算法
2020 年,Xue 等[15]提出一种新兴群智能算法——麻雀搜索算法(Sparrow search algorithm,SSA),具有操作简单、强鲁棒性和稳定性好等优点,普遍被用于工程领域,因此选择SSA 算法为认知工业物联网用户寻找最佳频谱分配方案。
本节针对标准麻雀搜索算法收敛速度慢、易陷入局部极值和寻优精度不高等问题,提出一种改进二进制麻雀搜索算法(IBSSA)。
标准SSA 算法由发现者、加入者和侦察者组成。SSA 中的发现者负责寻找食物,并且为整个麻雀种群提供觅食区域和方向。但是发现者在搜索食物的过程中,麻雀可能受地形干扰,影响其寻找食物,不利于麻雀快速向最优目标靠近。鸽群算法[16]的地图指南针算子可以引导偏离目标位置的麻雀感知目标方向寻找食物。于是将鸽群算法的地图指南针算子嵌入发现者位置更新公式,来提高收敛速度,增强跳出局部最优能力,计算公式如式(8)所示。

式中:l为当前迭代次数;L为最大迭代次数;α为范围0 到1 的随机数;R2(R2∈[0,1])表示预警值;ST(ST∈[0.5,1])表示安全值;Q为服从正态分布的随机数;R为1×d的矩阵,其中每个元素都为1;R是鸽群算法的地图指南针因子,R越小,强度越强,搜索能力就越强、发展潜力越大,Rmax表示最大地图指南针因子值,Rmin表示最小地图指南针因子值;pr为变异概率;rand 为[0,1]之间的随机数。但是传统的地图指南针算子属于线性变化,对每只麻雀赋予相同的值,并没有考虑麻雀在不同位置所处的差异,因此对地图指南针算子进行改进

式中:WorstF 为麻雀最差适应度值,BestF 为麻雀最佳适应度值。麻雀最差适应度值与最佳适应度值之比反映不同麻雀的位置差异,使麻雀能更好地寻找到目标值。
SSA 中的加入者察觉发现者找到优质食物时,会立刻离开当前位置去争夺食物,其位置更新公式为

式中:xworst(l)表示当前全局最差位置,xbestj(l)表示在j维空间第i个发现者占据的最佳位置,A表示一个1×d矩阵,随机分配元素1 或-1,其中A+=AT(AAT)-1。当i>n/2 时,表示适应度值较差的第i只加入者处于饥饿状态,它需要飞往其他方向寻找食物。
当麻雀种群觅食时,会选取一部分种群负责侦查周围情况,SSA 中的侦查者占全部种群的10%~20%,在侦查者位置更新公式(12)中,β作为步长控制参数,对平衡算法局部开发能力和全局搜索能力起着重大作用。但是β为一个随机数,并不能满足算法不同时期的需求,不同的β会对麻雀寻优性能造成影响。因此,对步长控制参数β进行优化,改进公式如(13)所示。

式中:K∈[0,1]表示麻雀运动方向,也是步长控制参数;fi表示当前麻雀的适应度值;fg和fw分别表示当前全局最优值和最差值;e为一个常数。当fi=fg时,表示处于种群中间位置的麻雀意识到危险,因此需要靠近其他麻雀来减少被捕食的概率。βmax为步长因子最大值,βmin为步长因子最小值。β的曲线变化图如图2 所示,它随着迭代次数增大而慢慢减小,当迭代开始时β的初值最大且递减速度很快,有利于进行全局探索,提高收敛速度;迭代后期β值较小且递减速度缓慢易于局部探索,提升SSA 的寻优能力。

图2 步长因子变化趋势图Fig.2 Chart of step factor change
由于CIIOT 中的频谱分配矩阵X是由0 和1 构成的离散二维矩阵,但在标准麻雀算法中麻雀的位置是连续的,所以需要对麻雀位置进行离散处理。然后将每个麻雀的离散位置最优解映射到频谱分配矩阵X={(n,m)|xn,m}N×M中。并且将麻雀个体适应度函数作为频谱分配的目标函数。
大多数文献使用Sigmoid 函数进行离散转换,而本文使用呈V 形变化的反正切双曲时变传递函数(TH)[17]将连续值转换为离散值,相较于Sigmoid 函数,TH 函数的优点在于不会强制麻雀位置转换为0或1 的值,并且TH 函数在避免陷入局部极值方面优于Sigmoid 函数,位置更新公式为

式中θmax和θmin分别表示控制参数的最大值和最小值,参考文献[18],将θmax和θmin分别设置为2 和0.1。引入动态传递函数后,在优化过程中,算法在迭代早期将重点放在探索上,以避免落入局部点,但是在算法后期,则更多地关注于开发以提高算法解的质量。
为了验证改进二进制麻雀搜索算法(IBSSA)的性能,对表1 所示的4 个测试函数进行求解寻优,故将IBSSA 与二进制麻雀算法(Binary sparrow search algorithm,BSSA)和二进制蝙蝠算法[19](Binary bat algorithm,BBA)的结果进行对比分析。利用单峰函数F1 和F2 来验证算法的收敛性能,多峰函数F3 和F4 验证算法跳出局部最优能力。将IBSSA、BSSA 和BBA 求解寻优函数所得的平均值和标准差作为评价指标,结果如表2 所示。并且为了使仿真测试的公平性令人信服,将所有算法的共同参数均设置相同:种群大小N=50,迭代次数最大为L=300,空间维数D=30。

表1 基准测试函数Table 1 Benchmark function
从表2 可以看出,与BSSA 和BBA 相比,对于求解单峰函数F1,IBSSA 求解精度已达到理想值,对于求解F2,IBSSA 虽没有达到理想值,但IBSSA 的最优求解性至少高于BSSA 和BBA 两个数量级,且相较其他算法,IBSSA 的标准差小于其他3 种算法,说明IBSSA 在求解单峰函数方面拥有更好的寻优能力和稳定性。对于求解多峰函数F3 和F4,IBSSA 的寻优精度均高于BSSA和BBA,且标准差为0,说明IBSSA 有良好的稳定性,不易陷于局部陷阱,能得到较好的解。由此得出结论,IBSSA 无论面对简单问题还是多维问题都表现出较高的寻优性能。

表2 实验结果Table 2 Experimental results
3 频谱分配和功率控制
3.1 基于IBSSA 的频谱分配策略
针对CIIOT 频谱分配优化问题,本文提出基于IBSSA 算法的频谱分配策略,将频谱分配[20]映射到麻雀种群中个体的位置,以进行频谱管理,最佳种群解与频谱分配的能量效率和认知用户之间的公平性指数相对应。所以,频谱分配问题的最终优化目标是在最大化系统能量效率和用户公平性的情况下,求解无干扰分配矩阵X[21]。因为可用矩阵U会约束着信道分配矩阵X,所以根据空闲矩阵中次用户使用信道的情况,当un,m=0 时,表明在目前通信状况下次用户n不能占用频谱m,而可用矩阵P中的0元素在位置上与矩阵X的0 元素对应,xn,m=0。因此,只需要对可用矩阵U中值为1 的元素实行编码。矩阵U中元素为1 的总数决定麻雀的编码长度L,其数学公式为

如图3 所示,假设在系统中认知用户数N=4,可用频谱数M=4,矩阵U通过检测频谱被获取,然后在矩阵U中抽取元素为1 的值进行编码,得到解向量x={xi∈(0,1),i=1,2,…,7},最后将麻雀个体的解向量与分配矩阵X映射。因为麻雀个体位置是随机生成的,按照这个编码方法并不能使每个分配方案成功,所以麻雀个体需遵守无干扰约束条件,任意频谱m(0≤m≤M)寻找满足条件gn,k,m=1的n和k,若X中xn,m和xk,m都为1,那么就把其中一个元素设置为0,另一个不变,这样就能解决频谱分配问题。

图3 解向量编码方式示例图Fig.3 An example of a de-vector encoding scheme
算法具体实现步骤如下:
(1)初始化麻雀参数和网络参数,例如主用户数、次用户数和信道数量等。
(2)产生主用户和次用户的位置拓扑图,生成可用矩阵U、效益矩阵E和干扰矩阵G。
(3)干扰约束处理,判断干扰矩阵G的元素两行元素是否为1,若为1,则随机把两行中的任意一行对应元素变为0,另一行仍为1。保证一个频谱分配给一个用户,将麻雀位置映射为分配矩阵X。
(4)计算种群最初的适应度值,对种群的历史最优、全局最优的适应度值进行保存,保存麻雀最佳位置及最优的频谱分配方案。
(5)根据式(8,10~13)进行种群更新,更新麻雀位置。根据式(14,16)将连续麻雀位置进行离散化,重复步骤3 根据干扰矩阵G进行干扰约束,然后根据目标函数计算所有麻雀的适应度值,选出具有最大适应度值的个体,迭代寻优。
(6)重复步骤4,5,当已达设置的最大迭代次数时,则返回迭代结束,并输出全局最优解,此时得到的全局最优解就是最佳频谱分配方案。
3.2 基于接收SINR 的闭环功率控制策略
系统模型如图1 所示,在认知工业物联网中,CBS 和PBS 覆盖范围由于交叉重叠会产生干扰,为有效降低干扰的影响,本文采取的策略是:先利用开环功率控制算法对用户的发射功率进行初始化,再利用闭环功率控制算法动态调整用户的发射功率[22]。根据通信用户的信息参数,数据中心对其进行判断,给出对应的功率控制命令(TPC),用户会根据收到的指令,对其发射功率选择上加一个步长或下降一个步长来动态调节功率控制。因为用户的信息会发生变化,在调整功率控制的过程中,根据信道的实时变化,利用新加入的反馈项f(λi)来调整步长取值。认知工业物联网用户的开环功率控制和闭环功率控制数学表达式为
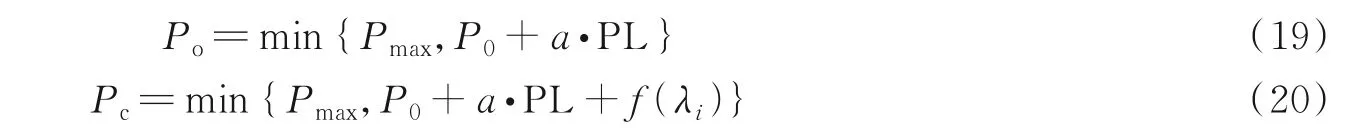
式中:a为路径补偿因子;PL 为路径损耗;Pmax表示用户最大传输功率;P0表示用户特定的额定参数,由文献[23]可知,P0设置为-78 dB 时,能达到最佳去干扰效果。在闭环功率控制中的f(λi)是根据λi来对功率进行上调或下调的动态调整,其数学表达式为

本文根据用户SINR 的动态变化,采用基于接收SINR 的闭环功率控制算法对功率控制进行动态调节。由用户当前的SINR 和反馈项f(λi)来确认闭环功率控制算法的参数。设置SINR 门限值SNRlow和SNRhigh,将当前SINR 同SNRlow和SNRhigh比较,根据经验取值,将下限值SINRlow和上限值SINRhigh分别设置为-20 和30 dB,当SINR
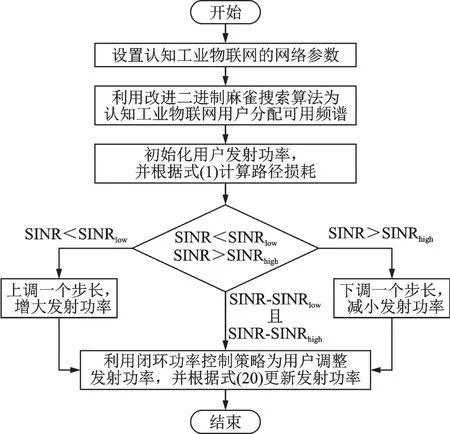
图4 算法流程图Fig.4 Flow chart of algorithm
为了证明基于接收SINR 闭环功率控制的频谱分配有效性,将改进二进制麻雀搜索算法联合基于接收SINR 的闭环功率控制策略(IBSSA-SCLPC)、改进二进制麻雀搜索算法联合开环功率控制策略(IBSSA-OLPC)和基于改进二进制麻雀搜索算法的频谱分配策略(IBSSA)进行比较。系统用户效益值能直接反映用户所受的干扰,所以将系统用户效益为优化目标。图5 为不同策略下的用户系统效益对比图。由图5 可知,系统效益随着迭代次数的增加而增大,IBSSA-SCLPC 的系统效益最高,而IBSSA-OLPC 次之,IBSSA 最差。这证明了功率控制可以有效地抑制用户间的干扰,基于接收SINR 的闭环功率控制策略的抑制效果优于IBSSA-OLPC,明显提高了用户系统效益。

图5 不同策略下用户系统效益对比图Fig.5 Chart of user system benefit under different strategies
3.3 算法复杂度分析
算法的时间复杂度反映了算法的有效性。虽然功率控制算法的复杂度会随认知工业物联网用户数目的增加而增加(复杂度为O(R)),但算法本身复杂度不大,不影响频谱的分配。所以只考虑IBSSA算法的时间复杂度。IBSSA 算法的复杂度取决于麻雀种群规模、最大迭代次数等参数。假设麻雀种群为N,适应度函数时间为t,在二进制转换过程,迭代次数为L1;在地图指南针算子中,迭代次数为L2;在自适应步长策略中,迭代次数为L3,则IBSSA 的算法复杂度为O(N×L1×t)+O(N×L2×t)+O(N×L3×t)。虽然IBSSA 与SSA 相比,计算复杂度有所增加,但IBSSA 算法增强了全局和局部搜索能力,所以对算法的改进是有价值的。
4 仿真实验与结果分析
为了验证所提出的频谱分配策略能有效解决工业物联网频谱稀缺和干扰的问题,本文将基于接收SINR 的闭环功率控制策略分别同SSA、BSSA 和BBA[19]结合,由于用户的干扰情况会受能量效率的多少影响,所以,以最大化能量效率和公平性为优化目标,分析是否得到较优的频谱分配方案,是否有效抑制干扰。仿真测试在MATLAB R2016 上进行,仿真设置网络区域范围为100×100,认知用户数N、可用信道数M和主用户数K的初始值都设为10。参考文献[24-26]设置系统模型每个仿真参数,如表3 所示。

表3 仿真参数设置Table 3 Simulation parameter setting
图6 表示基于不同群智能算法的频谱资源策略,从图6 的曲线趋势可知,能量效率会跟着迭代次数的增大而增大,基于IBSSA 的频谱分配方案的能量效率最大,BSSA 次之,BBA 最差。且IBSSA 在3 种频谱分配方案中是最快收敛,得到认知工业物联网中频谱分配问题的最优解。
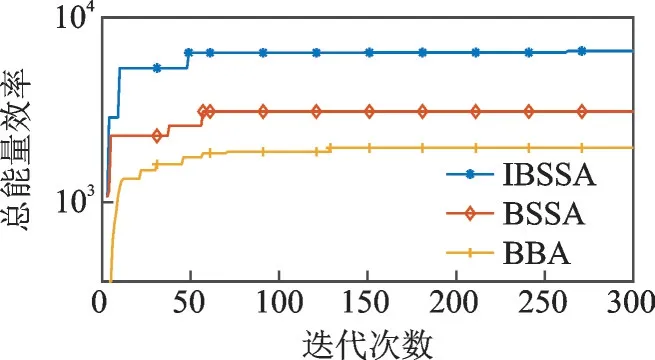
图6 不同算法能量效率对比图Fig.6 Chart of energy efficiency of different algorithms
为了表明不管在什么网络环境下,IBSSA 算法均具有更优的公平性,在认知用户数与可用频谱数相等都为10 时,将3种算法在30 次不同网络环境下进行仿真,图7 表示不同信道环境下的Jain’s 公平指数对比图。从图7 可以看出,在不同的信道环境下,IBSSA 算法的公平性均大于BSSA 和BBA 算法。

图7 不同环境下的Jain’s 公平指数Fig.7 Jain’s fair index under different algorithms
图8 表示算法的能量效率与最大发射功率之间的联系,将不同发射功率下的能量效率独立运行30 次取平均值进行比较。由图8 可知,最初能量效率会跟着最大发射功率一起增加。当最大发射功率Pmax=24 时,3 种算法的能量效率都达到各自的最大(IBSSA 的能量效率最高)后,能量效率开始随着Pmax的增加而减小。虽然能量效率开始下降,但不管最大发射功率为何值,IBSSA 的能量效率都优于BSSA 和BBA。

图8 3 种算法在不同发射功率条件下的能量效率Fig.8 Energy efficiency of three algorithms in different transmitting powers
图9 表示在最大发射功率Pmax=24 时,路径损耗因子a变化,3 种算法的能量效率也会跟着变化,将不同路径损耗因子下的能量效率独立运行30 次取平均值进行比较。从图9 可知,当a增大时,能量效率会跟着减小,这是因为路径损耗因子的增大会导致信号在传输中的损耗也增大了,导致能量效率降低。但是IBSSA 的能量效率虽降低,却始终优于其他算法。

图9 3 种算法不同路径损耗因子下的能量效率Fig.9 Energy efficiency of three algorithms in different path loss factors
图10 表示SINR 上限值对平均能量效率的影响,从图10 的变化趋势可看出,随着SINR 的增加平均能量效率也随着增大,在3 种算法中,IBSSA 的平均能量效率最高,BSSA 次之,BBA 最差。由此可知,信干噪比值的大小可以影响平均能量效率,并且设置的信干噪比越高,则越有利于认知工业物联网用户的通信。因为SINR 值越高,那么认知工业物联网用户的功率就不须要减小1 dB,使得认知用户通信性能良好。

图10 3 种算法不同信干噪比下的平均能量效率Fig.10 Average energy efficiency of three algorithms in different signal-to-dryness ratios
图11 表示不同发射频率波长对平均能量效率的影响,从图11 的曲线趋势可以看出,随着发射频率波长的增加平均能量效率也随之增大,直到发射频率波长为0.6 m 时,平均能量效率达到最大,随后开始下降。并且在不同的发射频率下,IBSSA 的平均能量效率都优于其他算法,这证明了本文提出的IBSSA 能使网络性能达到更优。
5 结束语
本文针对工业物联网中的频谱资源稀缺问题,提出一种联合IBSSA 算法和闭环功率控制的频谱分配策略。首先对麻雀搜索算法进行优化,解决麻雀算法面对多维函数求解精度不高、易陷于局部陷阱等问题。然后采用闭环功率控制算法减少认知工业物联网中用户之间产生的干扰。最后将改进二进制麻雀搜索算法与闭环功率控制结合来进行频谱分配。实验仿真结果表明,改进后的麻雀搜索算法的收敛速度得到了提高,同时本文所提的改进方案能有效提高系统能量效率和公平性,减少干扰。在未来的工作中,将研究CIIOT 中多对用户的动态资源分配,基于网络吞吐量优化进行资源分配。
