基于Bouc-wen模型的阻尼器建模仿真

周鑫林 杨洪永 张强

珠海格力电器股份有限公司 广东珠海 519070

0 引言

随着计算机技术的发展，虚拟样机技术被广泛应用于分析结构设计的可靠性、合理性。利用CAD软件设计原型样机，在计算机中模拟机械结构的运动并分析其受力情况，然后根据仿真结果对原型样机进行优化以达到指导设计的目的。但是在洗衣机的设计中，阻尼减振器的受力情况比较复杂，呈现出非线性特征，对仿真结果的精度有较大影响，需要技术人员自行建模处理。Nygards等人对洗衣机结构进行分析并建立仿真模型，确定了阻尼力的数学模型，给出了阻尼力的测试方案[1][2]。朱耀辉认为阻尼力由干摩擦力和黏滞阻尼两部分组成，利用Bingham模型对阻尼力进行仿真，结果表明黏滞阻尼系数在同一激振力作用下具有较好的一致性[3]。曹然采用Bouc-wen模型对阻尼器进行研究，通过测试数据辨识模型参数，并分析不同工况条件下的参数的变化规律[4]。M.T.Braz-César等人分别使用Bingham模型、Bouc-wen模型对MR阻尼器进行建模，并对比测试数据，结果表明Bouc-wen模型对非线性阻尼力-速度的迟滞效应描述更加准确[5]。周幪幪等人对阻尼器衬套进行建模，探究阻尼器衬套对洗衣机的运动情况的影响[6]。本文基于Bouc-wen模型对洗衣机的阻尼器进行建模，并测试洗衣机阻尼器的特性曲线。采用遗传算法，对Bouc-wen模型的参数进行辨识，以此研究洗衣机阻尼器在虚拟样机中的建模方法。所提模型能够模拟阻尼力的变化情况，仿真结果与测试结果对比误差较小。

1 阻尼器测试实验

阻尼器由三个部分组成，其中外筒固定于洗衣机滚筒，摩擦片置于外筒内壁，内筒固定于框架。阻尼器实物如图1所示。阻尼器工作时外筒相对内筒滑动但不与内筒接触，通过摩擦片与内筒摩擦产生阻尼力。当阻尼器处于静止阶段时，由于没有相对滑动，阻尼器不产生阻尼力；当阻尼器处于从静止到滑动阶段时，摩擦片产生弹性形变，阻尼器产生弹性力；当阻尼器处于滑动阶段时，摩擦片同时存在滑动摩擦和弹性形变，阻尼器产生弹性力和摩擦力。阻尼器通过摩擦力做功耗散振动能量。因此将阻尼力简化为三个部分，黏滞阻尼、弹性力以及摩擦产生的迟滞效应，如图2所示。其中M为阻尼器外筒的质量，m为阻尼器内筒的质量，C2为阻尼器衬套的阻尼，F(t)为阻尼器的阻尼力，K为弹性力的刚度，C1为黏滞阻尼的阻尼系数，迟滞特性为Bouc-wen模型。

图1 阻尼器实物

图2 阻尼器简化模型

通过测量阻尼器对输入的响应，识别Bouc-wen模型中的未知参数。测试仪器采用拉伸疲劳试验机，固定阻尼器的内筒，夹持阻尼器的外筒进行往复运动。考虑到阻尼器的工作方式，将输入定为外筒的位移，测试阻尼器外筒的速度和阻尼力。输入位移采用正弦函数，频率与幅值如表1所示。

表1 正弦输入的频率与幅值

滚筒洗衣机悬挂结构通常在转速180 rpm～240 rpm区间内产生共振，其转频为3 Hz～4 Hz，因此选择在该频率段进行研究。

测试结果如图3所示，图3 a）和b）分别为阻尼力-位移曲线，阻尼力-速度曲线。从图3 a）和b）可以看出，80 N阻尼器的阻尼力-位移曲线形状近似平行四边形，阻尼器外筒位移为0处对应阻尼力的最大值，此时阻尼器内、外筒相对速度约为60 mm/s，当阻尼器内、外筒相对速度约为0 mm/s时，位移约为3 mm。

其次，在阻尼器运动过程中，阻尼力的大小、方向虽然会发生变化，但这一转变过程持续时间较短。图3 a）中位移-2 mm到2 mm区间曲线的斜率趋近于0 N/mm和图3 b）中速度在-40 mm/s到40 mm/s区间曲线的斜率趋近于0 N/(mm/s)，可以看出当阻尼力接近或达到最大值60 N时，位移和速度的变化对阻尼力值影响比较小。

图3 阻尼器特性曲线

另外，从阻尼力-速度曲线可得，阻尼力的最大值不会随相对速度的增加而产生明显变化，说明在该频率下，阻尼力表现出的黏滞性较小，阻尼力以摩擦力为主。

2 Bouc-wen模型辨识

Bouc-wen模型是1阶非线性微分方程，被广泛应用于描述非线性迟滞系统，其数学表达式为[7]：

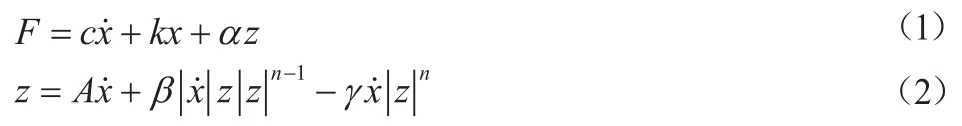
其中，F代表阻尼力，c代表阻尼系数，k代表刚度系数，z代表迟滞项，α、A、β、γ是与迟滞项z相关的常系数，n为滞回曲线光滑程度系数。但实际上摩擦片的弹性形变相当小，刚度项可忽略不计，式（1）亦可改写为：

2.1 遗传算法辨识

遗传算法是一种模拟生物遗传进化机理的自适应启发式概率性迭代全局搜索算法。遗传算法会随机选择初始模型参数并对其进行编码，选择其中计算结果最优的参数随机组合，再从中选择计算结果最优解。通过反复操作，得到全局最优的模型参数。与传统搜索算法不同，遗传算法无需利用目标函数的导数值作为辅助信息确定搜索方向，只需要将目标函数的函数值转化为适应度函数值，即可确定下一步搜索方向。

本文采用二进制对表2中六个参数进行编码，形成染色体，参数的初始值取值范围见表2，参数的值随机选取。初始种群数量为50，迭代计算次数为120。

通过适应度函数赋予每条染色体一个适应度值，选择初始种群中适应度值较大的染色体作为父代。通过两点交叉法，将两个父代染色体的部分基因互换生成两个新的子代染色体，设置变异率为2%。

选择遗传算法的目标函数为：

其中，m是数据点的数量，Fexp代表实验得到的阻尼力值，Fcal代表数学模型计算得到的阻尼力值。目标函数求取e的最小值，即实验值与计算值误差最小。对e进行归一化得到适应度值。

以频率3 Hz振幅3 mm为例，Bouc-wen模型的辨识参数如表2所示。遗传算法辨识结果如图4所示。

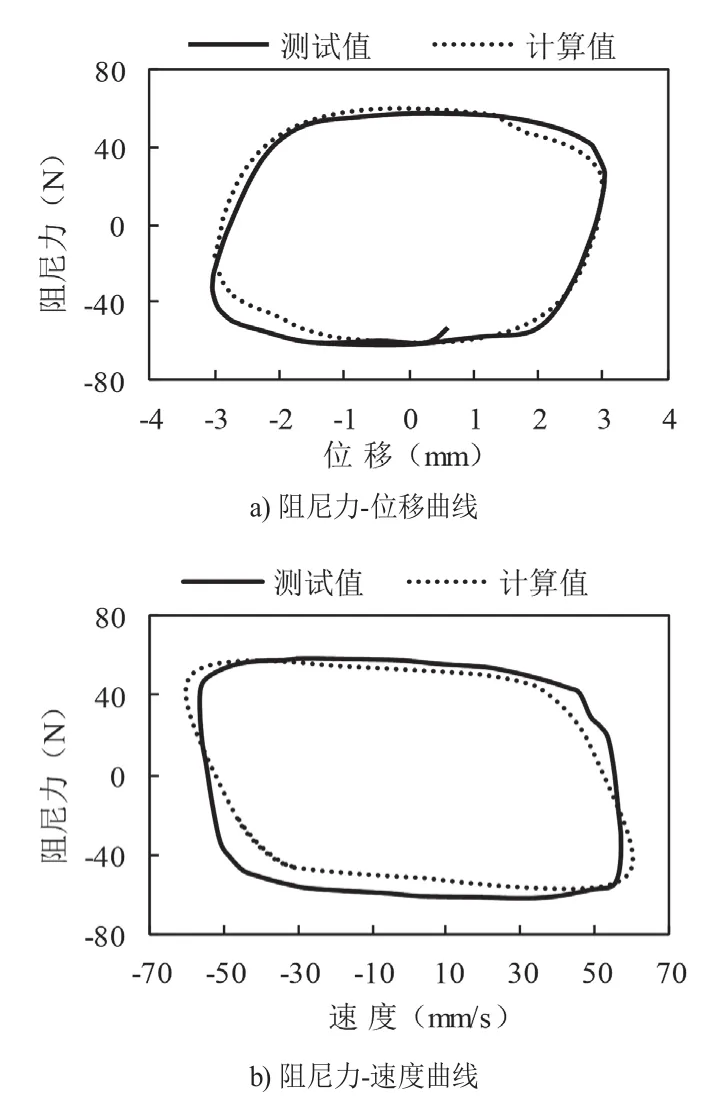
图4 遗传算法辨识结果

表2 Bouc-wen模型的辨识参数

通过与实验数据对比可得，遗传算法的计算值与实验测试值的曲线基本吻合，阻尼力的最大值误差较小，但在位移和速度最大值处的误差比较大。

2.2 神经网络建模

Bouc-wen模型需要辨识的参数数量比较多，具有较强的非线性，运用遗传算法求解参数，仍需要带入Bouc-wen模型求解一阶微分方程，因此求解速度相对缓慢。针对以上问题，可以基于测试数据，采用神经网络进行建模。已知阻尼器的阻尼力与其位移和速度呈现出非线性关系，将位移和速度作为神经网络输入，将测试得到对应的阻尼力值作为神经网络的理想跟踪目标，神经网络的输出为阻尼力逼近值。神经网络的优势在于无需求解微分方程，计算方法更加简单。

本文采用径向基函数（RBF）神经网络，它是一种单隐层三层前馈网络，可以加快神经网络的学习速度并避免陷入局部最小问题。将阻尼器内、外筒的相对位移和速度定义为神经网络的输入，传递给隐含层。隐含层为多个高斯基函数，神经网络输出为阻尼器阻尼力。RBF网络结构图如图5所示。

图5 神经网络结构

隐含层高斯基函数hj公式如下：

其中，Cj为高斯基函数的中心值，bj为高斯基函数的宽度值。

神经网络输出层如下，其中Wj为神经网络权值。

选择目标函数如下：

当E的值无限趋近于0时，表示神经网络的输出值逼近于实验测试值。

神经网络中的Cj、bj以及Wj三个参数需要通过算法迭代调整，公式如下[8]：

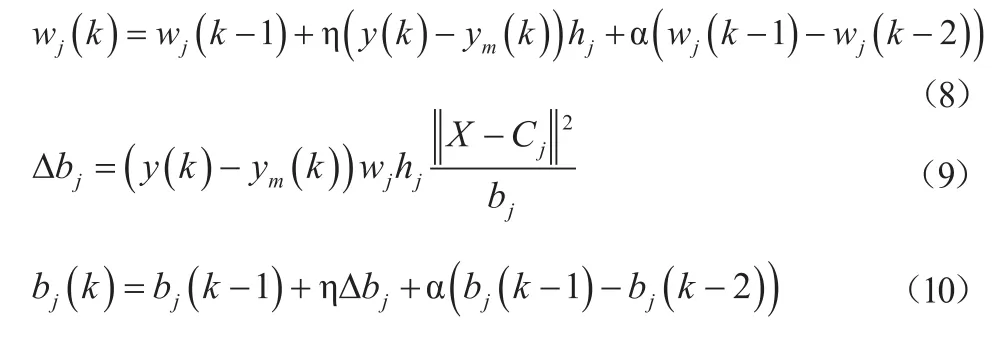
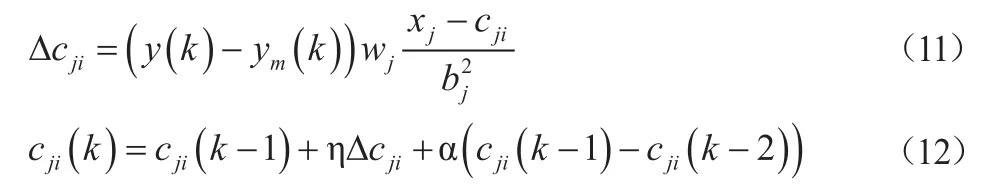
其中，η、σ分别为学习速率、动量因子。

网络隐含层节点数取6，取Cj、bj以及Wj三个参数的初始值Cj=[0.5, 0.5, 0.5, 0.5, 0.5, 0.5]，宽度值bj=[5, 5, 5, 5, 5, 5]，权值Wj=[0.5, 0.5, 0.5, 0.5, 0.5, 0.5]T，η取0.35，σ取0.45。RBF神经网络仿真结果如图6所示。

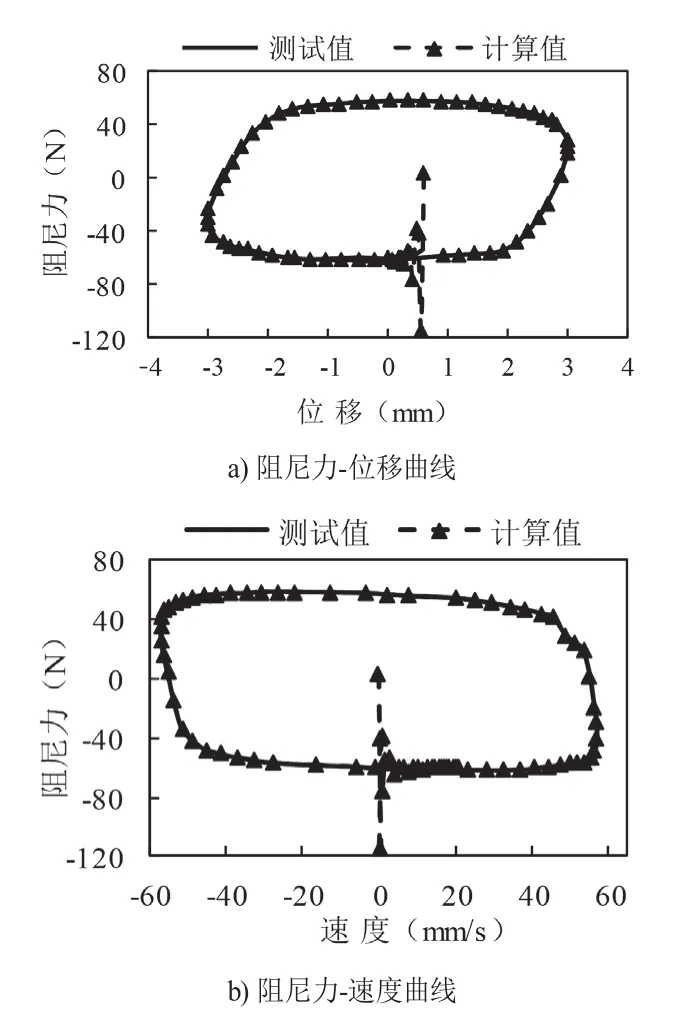
图6 神经网络逼近结果

从仿真结果可得，在神经网络逼近的初期误差较大，但是能够迅速逼近测试值，令计算值与测试值基本重合。即使在位移和速度最大值处，神经网络的逼近效果也会比遗传算法更好。

3 结论

本文研究了遗传算法和RBF神经网络在洗衣机阻尼器建模中的应用，结果表明，RBF神经网络通过自适应调整中心值、宽度值和权值，更快得到合适的参数值，且逼近效果比遗传算法更好。另外，RBF神经网络的计算方式更加简单，与遗传算法相比，无需求解微分方程，因此求解速度更快，可以减轻洗衣机整机仿真的计算难度。

阻尼器通过滑动摩擦抑制洗衣机运行过程中产生的振动，但是阻尼器的滑动速度与摩擦产生的热量会影响阻尼器的滑动摩擦系数。而本文在对阻尼器建模计算的过程中，主要考虑阻尼器低速滑动的工况，并未考虑阻尼器的滑动速度以及温度对阻尼系数的影响。后续可以展开相关的研究。