基于有限元的冰箱门体变形仿真与优化研究

孙启东 韩丽丽 张升刚 张月

海信（山东）冰箱有限公司 山东青岛 266071

0 引言

自20世纪50年代我国开始生产冰箱以来，经过几十载的研究与发展，冰箱现如今已经广泛分布于千家万户，成为家庭生活必备产品之一。同时，随着中国经济的快速发展和居民可自由支配收入的增多，人们的生活水平不断提升，对生鲜食材的健康保鲜需要越来越高，从而促使对冰箱的需求量越来越大。截至2020年，中国冰箱销量已达8447万台，较2019年增加了709万台，同比增长9.2%，并呈逐年增加的趋势，如图1所示[1]。

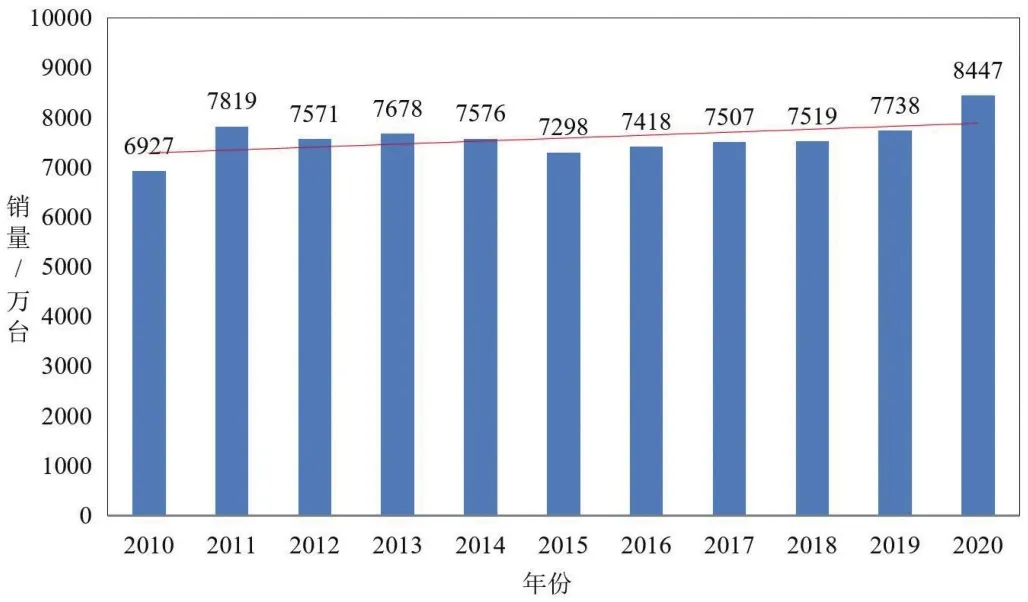
图1 2010—2020年中国冰箱销量统计及发展趋势

针对国民日益增长的消费需求，国内冰箱厂家均增加了产量。但在冰箱的生产过程中仍存在诸多问题，其中冰箱门体变形就是困扰厂家的一个很大的问题。冰箱门体生产的一个关键步骤就是高温发泡，从发泡开始到完全冷却，门体要经历很大的温度变化，由于门体各组成部件的材料不同，其在较大的温差下会产生不同程度的膨胀收缩，导致门体发生变形。虽然变形的门体在质检时将会被剔除，但这无疑增加了企业的生产成本，打乱了生产节奏。而有限元仿真分析作为广泛应用的实用技术在门体设计初期就可以很好的解决这一问题。

李乾坤等[2]建立了聚氨酯注塑充型流动的数学模型，研究了聚氨酯在门体中的填充状况。郭刚等[3]基于热力耦合的有限元方法，提出了通过优化内胆结构来抑制门体变形。张艳玲等[4]运用有限元法对发泡门体的冷却变形状态进行了数值模拟分析，得出冷却变形后某些局部点收缩变形的精确数据。洪在地等[5]借助MSC.MARC有限元软件研究了冰箱门体的变形机理，并提出了相关解决办法。

本文针对冰箱门体发泡过程中变形的实际问题，借助有限元分析软件对冰箱门体发泡过程进行仿真模拟，并在此基础上探究了降低门体发泡变形的方法。同时，将计算结果与实际实验数据进行了对比，确保了仿真结果的准确性。

1 热变形理论

冰箱门体在发泡过程中会经历较大的温度变化，这就涉及热传递问题。结合传热学原理可知，对于三维模型来说，传热控制方程[6]可表示为：

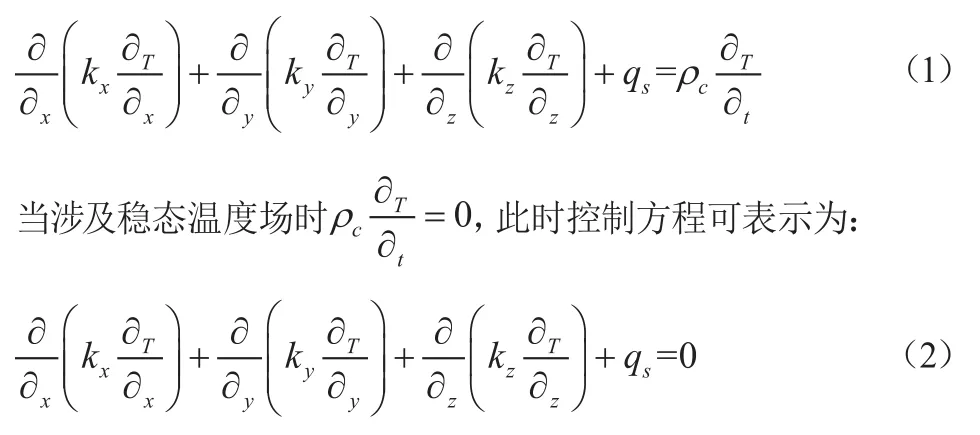
式中：kx，ky，kz分别为材料在x、y、z方向上的传热系数，单位为W·m-1·K-1；T为每个节处的温度，单位为℃；qs为热源强度，也就是单位体积产热率。

当物体内部存在温差ΔT(x,y,z)时，由于材料的热膨胀系数不同，温差会导致物体的热膨胀收缩不均匀，因此会产生一个膨胀值αT ΔT(x,y,z)，即物体产生形变，则该物体的物理方程为[7]：

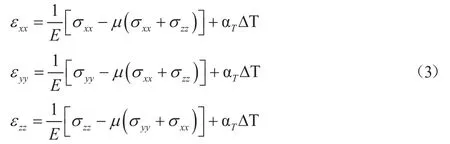
式中：ε为热应变，E为杨氏模量，μ为泊松比，σ为热应力，αT为热膨胀系数。

2 有限元模型的建立

本文选择我司某款玻璃门冰箱来进行研究，冰箱门体的尺寸为高×宽×厚=1436 mm×611 mm×89.5 mm，冰箱门体具体结构如图2所示，主要由门内胆、发泡层、门玻璃、控制盒、门端盖和门拉手组成。在分析的过程中，为节约计算资源对冰箱门体进行了必要的简化。

图2 冰箱玻璃门结构示意图

在有限元分析前需进行网格划分并检查网格质量，以确保计算结果的准确性，本文中门体发泡层部分使用四面体单元划分，门内胆、边框、端盖、玻璃门板则采用与实体单元共节点的壳体单元，总网格单元数量约为130万个。本文分析所采用的材料属性如表1所示。在进行有限元分析时，将位移边界条件设置在门玻璃上下两边，对垂直于面板方向的自由度施加位移约束；同时将温度边界条件设置到整个门体上，从发泡开始至完全冷却过程中门体要经历由80℃降至10℃的温度变化。

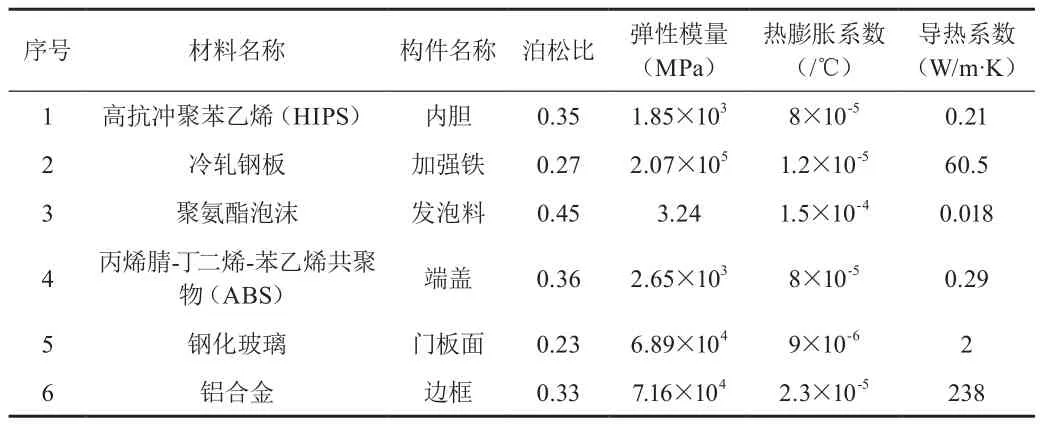
表1 材料属性

为减小门体在发泡至完全冷却过程中产生的变形，本文提出了几种优化方案并结合仿真与实验进行了验证，方案具体实施如图3所示。

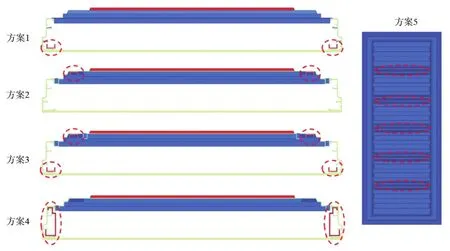
图3 改进方案具体排布示意图

方案1，在门体内部左右边框靠近面板一侧各增加一根U形加强铁。

方案2，在门体内部左右边框靠近内胆一侧各增加一根U形加强铁。

方案3，结合方案1与方案2，在门体内部左右边框靠近面板和内胆侧均增加一根U形加强铁。

方案4，在门体内部左右边框靠内各增加一根C形加强铁。

方案5，不使用加强铁，更改内胆结构，增加去应力槽的数量。

3 结果与分析

冰箱玻璃门从开始发泡至完全冷却的过程中，整体温度由80℃降低至10℃。如图4所示为冰箱门体原始结构变形情况（变形因子×10），由图4 a）可知门体整体变形呈现出沿Y方向拱起（即冰箱门面板一侧），最大变形量为11.40 mm，位于门体中央；门体两端变形较小。图4 b）为冰箱门体边框的变形情况，这也是最主要的关注点，由图可知边框最大变形量为7.74 mm，位于边框的中间位置。由此可见在门体发泡结束后会产生很大的变形，难以满足出场要求。因此十分有必要针对门体进行优化以减小发泡后门体变形的状况。

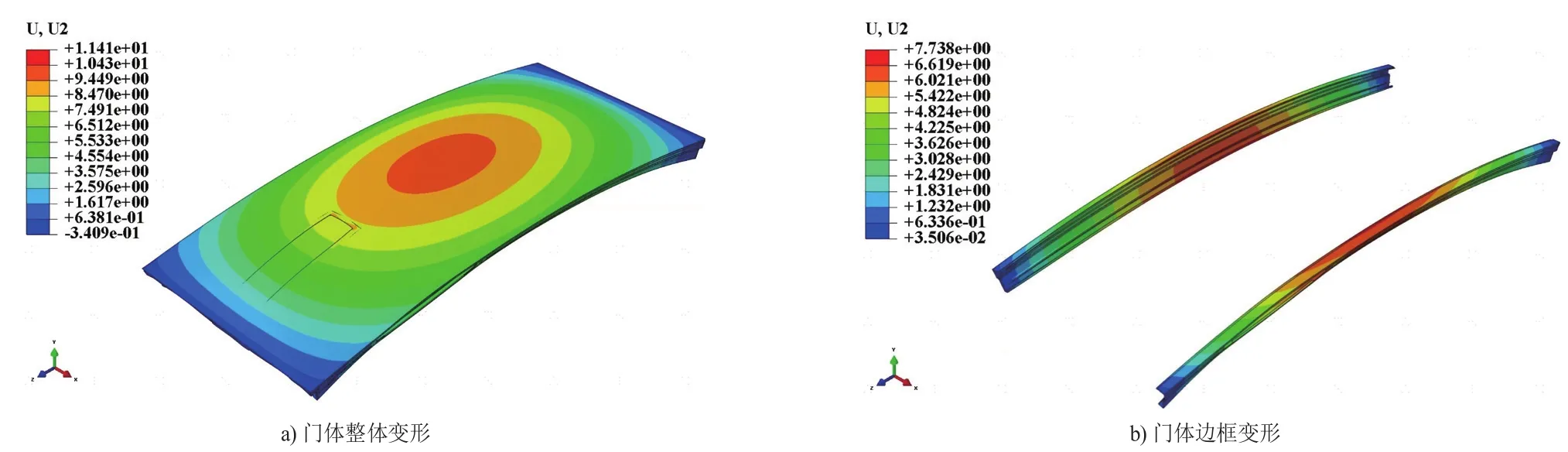
图4 原始门体结构发泡过程门体变形情况

为改善冰箱门体变形状况，提出五种优化方案。如图5～图9所示分别为冰箱门体在不同优化方案下的变形情况。如图5 a）所示为采取方案1进行优化时冰箱门体的整体变形，表现为沿Y方向拱起，最大变形量为10.30 mm；如图5 b）所示为采取方案1进行优化时门体边框的变形，最大变形量为7.39 mm，相比于原始结构变形减小了0.35 mm。

图5 优化方案1下的门体变形

如图6 a）所示为采取方案2进行优化时冰箱门体的整体变形，表现为沿Y方向拱起，最大变形量为9.20 mm；如图6 b）所示为采取方案2进行优化时门体边框的变形，最大变形量为6.31 mm，相比于原始结构变形减小了1.43 mm。

图6 优化方案2下的门体变形

如图7 a）所示为采取方案3进行优化时冰箱门体的整体变形，表现为沿Y方向拱起，最大变形量为6.04 mm；如图7 b）所示为采取方案3进行优化时门体边框的变形，最大变形量为4.49 mm，相比于原始结构变形减小了3.25 mm。

图7 优化方案3下的门体变形

如图8 a）所示为采取方案4进行优化时冰箱门体的整体变形，表现为沿Y方向拱起，最大变形量为9.65 mm；如图8 b）所示为采取方案4进行优化时门体边框的变形，最大变形量为6.20 mm，相比于原始结构变形减小了1.54 mm。

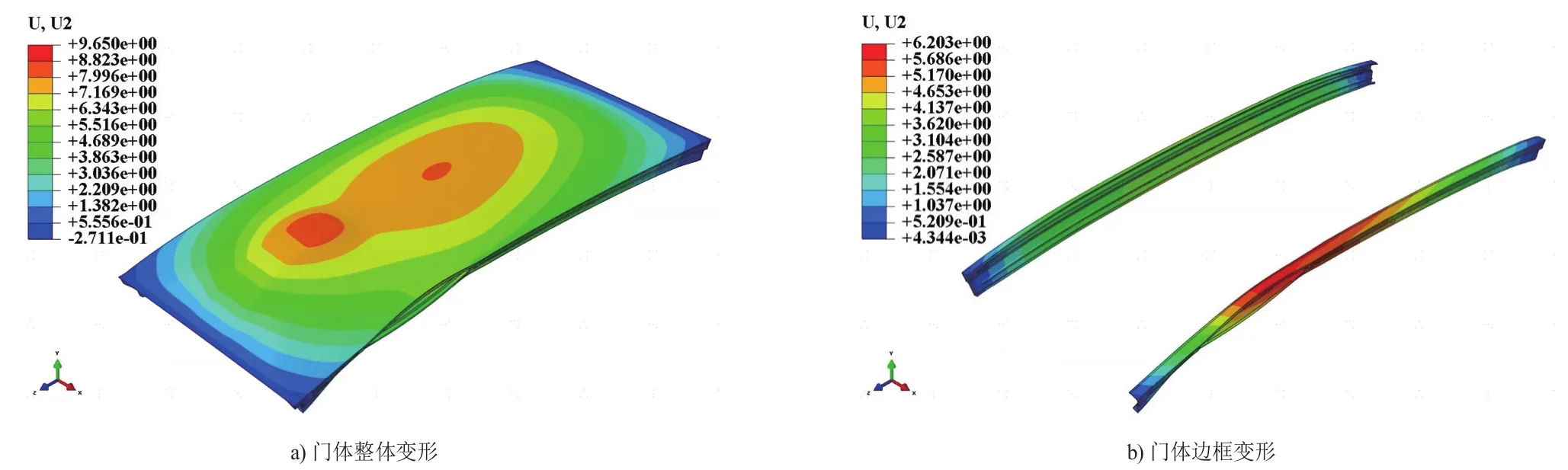
图8 优化方案4下的门体变形

如图9 a）所示为采取方案5进行优化时冰箱门体的整体变形，表现为沿Y方向拱起，最大变形量为10.40 mm；如图9 b）所示为采取方案5进行优化时门体边框的变形，最大变形量为7.32 mm，相比于原始结构变形减小了0.42 mm。

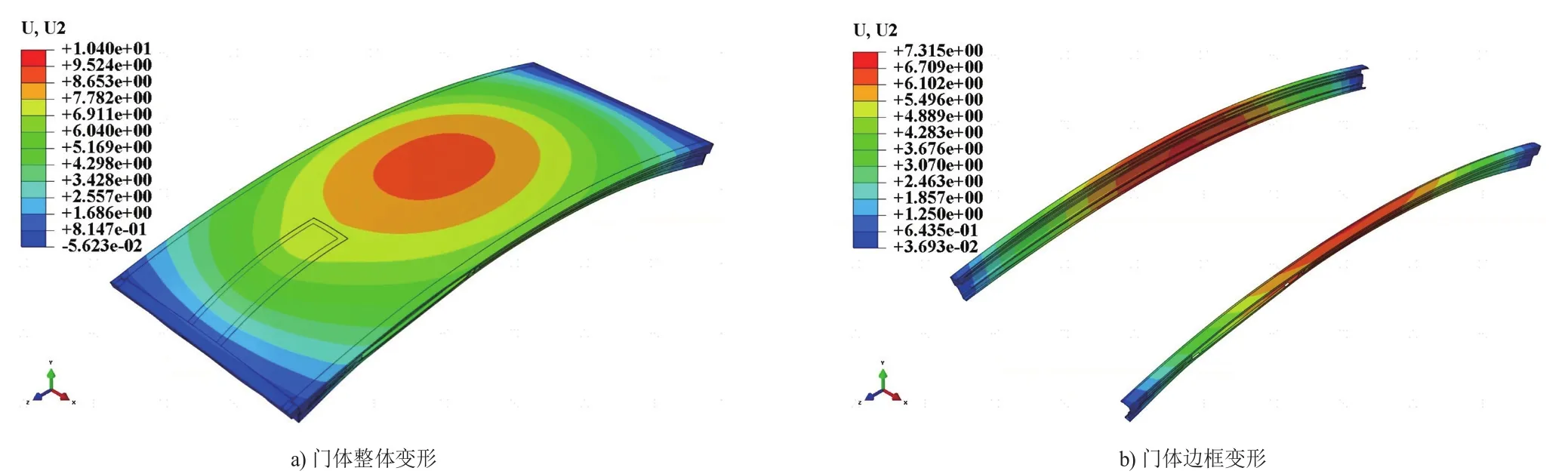
图9 优化方案5下的门体变形

为能够直观的对比各方案间的差别，现将各优化方案的变形量绘于同一图中，如图10所示为各方案与原始结构变形对比图。由图10可知相比于方案1，方案2对降低门体弯曲更有利，表明加强铁放置在门胆侧更有利于减小门体变形，分析认为是由于HIPS门胆的热膨胀系数远高于玻璃门板，致使门胆的膨胀收缩较大，加强铁放置在门胆处，能有效缓解其变形。由图10可得，方案3减小门体变形的效果是最明显的，表明增加加强铁的数量是最有效的方法。方案4的改善效果与方案2的效果相当，但方案4对加强铁的投入要高于其他方案，如更大的尺寸，更复杂的形状，因此就生产成本来说方案2更加符合需求。方案5的改善效果与方案1相差不大。

图10 原始结构与各方案对比

为验证仿真结果的准确性，分别将方案1至方案5于生产端进行了实际检验，将经过高低温实验后的冰箱门体水平放置，然后在门边框及门中心处塞入塞尺进行测量，实际测量数据如表2所示。从表2中可以看出，仿真结果略高于实际测量值，但两者误差均保持在13%左右，在工程允许范围内是可以接受的，因此仿真结果具有一定的准确性。

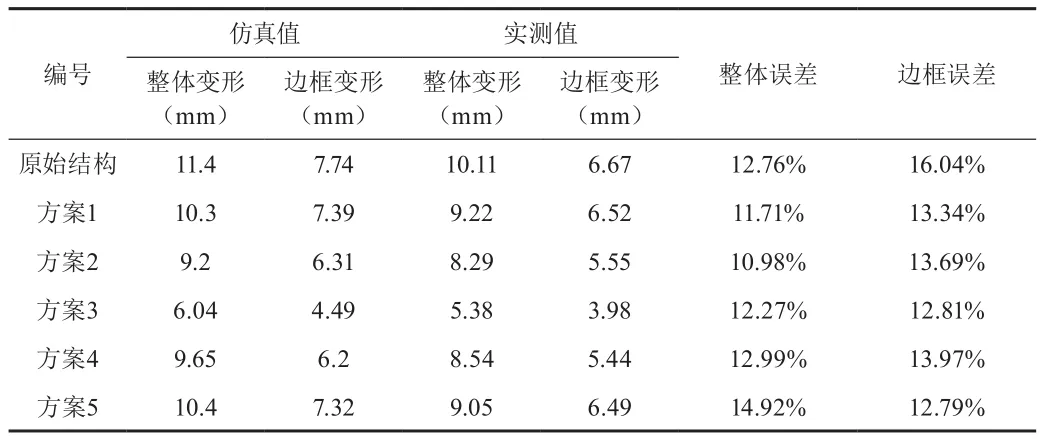
表2 仿真值与实测值对比

综上所述，加强铁的加入有利于降低冰箱门体的变形量，增加门胆去应力槽同样可以在一定程度上减小门体变形，但是其效果十分有限。

4 结论

本文以冰箱门体在发泡过程中的变形为研究对象，通过建立有限元模型，进行网格划分，边界条件设定以及求解计算，得到冰箱门体从发泡至完全冷却后的变形数据，并在此基础上提出优化方案。

研究结果表明，冰箱门体发泡完成后会产生弯曲变形，整体最大变形量达11.4 mm，边框最大变形量达7.74 mm，远远不能达到出厂要求。为解决这一问题，提出了5种优化方案。通过仿真与实验验证可知：在门体内部左右边框靠近面板和内胆侧各增加一根U形加强铁对门体变形的改善最佳，门体整体弯曲程度由原始的11.4 mm减小到6.04 mm，边框由7.74 mm减小到4.49 mm，达到了改善门体变形的目的。同时，证明了有限元分析方法不仅可以有效的辅助结构设计，而且能够帮助解决产品设计开发过程中存在的问题。