基于DPM的悬浮磁化焙烧主炉气固流动传热数值模拟

蔡玉节 孙永升，2，3 高 鹏，2，3 张 琦 唐志东

(1.东北大学资源与土木工程学院，辽宁 沈阳 110819;2.东北大学轧制技术及连轧自动化国家重点实验室，辽宁 沈阳 110819;3.难采选铁矿资源高效开发利用技术国家地方联合工程研究中心，辽宁 沈阳 110819)

悬浮磁化焙烧炉具有生产能力大、能耗低和自动化程度高等优点[1-2]，是目前处理褐铁矿、菱铁矿和微细粒赤铁矿等复杂难选铁矿石的有效装备之一[3-5]。物料的运输及加热过程主要在悬浮磁化焙烧主炉中实现，其内部气固流动与传热特性复杂。气固流动涵盖快速流态化、气力输送等流态化形式，传热方面不仅涉及气体与颗粒之间、颗粒与颗粒之间的传热，还涉及矿石颗粒本身化学反应吸放热，常规物理试验较难全面描述多因素耦合影响下的矿石颗粒流动和传热规律[6]。

随着计算机技术和数值模拟算法的快速发展，计算流体力学(Computational Fluid Dynamics，简 称CFD)已经发展成为一种研究复杂流动特性的常用手段。相比于理论分析和试验研究，CFD数值模拟方法具有效率高、成本低的优势，在冶金、化工、航天以及汽车等领域应用广泛[7-9]。

在工业数值模拟中，标准k-ɛ湍流模型具有较好的收敛速度和较低的计算内存要求，DPM(Discrete Phase Model)常用于离散相体积分数低于10%～12%的稀相气固流动数值模拟研究。为了探明悬浮磁化焙烧主炉中气相温度场分布、颗粒流动特性和颗粒升温速率等信息，基于数值模拟方法，本文采用标准k-ɛ湍流模型和DPM对悬浮磁化焙烧主炉进行数值模拟研究。

1 物理模型与网格划分

悬浮磁化焙烧主炉几何示意见图1，以底部空气入口为参考点，甲烷入口(燃烧室)位于0.55 m处，颗粒入口位于2.90 m处，顶部出口位于7.85 m处。利用ICEM CFD软件中的O-block功能完成了结构化网格的划分(图2)，并进行了网格无关性分析，最终确定网格数量为1 277 604。

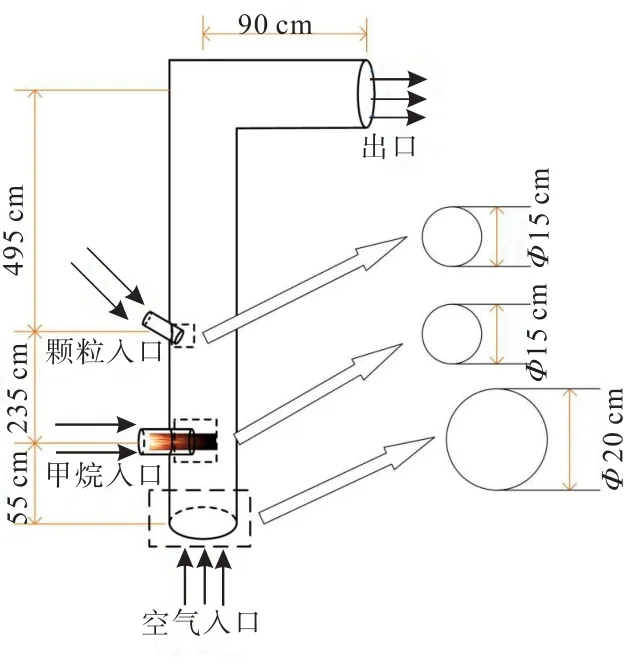
图1 悬浮磁化焙烧主炉几何示意Fig.1 Geometrical diagram of suspension magnetization roasting main furnace

图2 结构化网格划分Fig.2 Structured meshing

2 数学模型建立与边界条件设置

2.1 气相控制方程

本研究中气相的计算采用欧拉方法，控制方程主要包括质量守恒方程、动量守恒方程和能量守恒方程等。各控制方程的表达式如下[10]:

式中，T为温度，K;H为焓;ρf为流体密度，kg/m3;uf为速度，m/s，p为压力，Pa;Sh为包括了化学反应及其它用户定义的体积热源项;Г为有效耗散率，%;Ri为自定义源项;ω为孔隙率;μ为连续相动力黏度，N·s/m2。

2.2 颗粒相控制方程

本研究中颗粒相的计算，采用拉格朗日方法，颗粒相的运动追踪采用了Fluent软件中的DPM模型[11]。相比于颗粒受到的曳力，压力梯度力和虚拟质量力等其他形式的力小于3或4个数量级。因此，在本文模拟计算中仅考虑颗粒所受曳力，忽略了压力梯度力、虚拟质量力等其他形式的力[12]。颗粒相控制方程表达式如下:

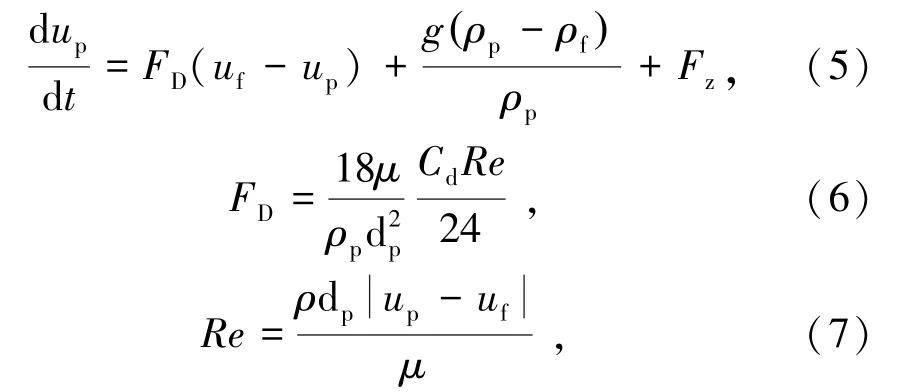
式中，mp为颗粒质量，kg;uf为流体速度，m/s;up为颗粒速度，m/s;ρf为流体密度，kg/m3;ρp为颗粒密度，kg/m3;Fz为附加力，N;μ为连续相动力黏度，N·s/m2;dp为颗粒直径，m;Re为颗粒雷诺数。

本研究中假设颗粒为光滑圆形颗粒，选择Spherical模型来计算曳力系数，具体表达式如下:

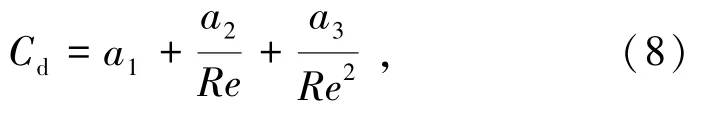
式中，Re为颗粒雷诺数;a1，a2，a3为常数[13]，不同的雷诺数范围内取值不同，具体如表1。

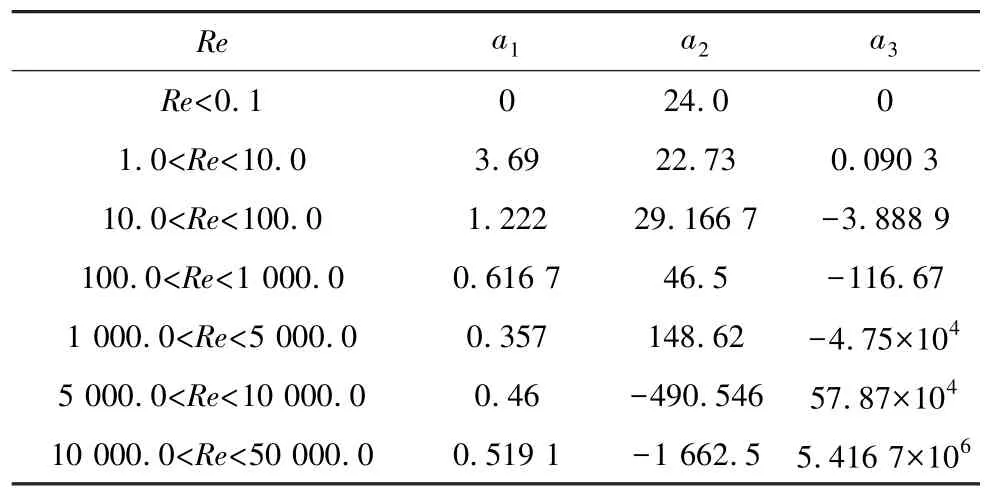
表 1 a1，a2，a3参数取值Table 1 a1，a2，a3 parameters value

2.3 气固传热模型

本研究中，使用热平衡方程来关联颗粒温度与颗粒表面的对流与辐射传热，具体表达式如下:

式中，假设颗粒内部热阻为0，各个位置温度一致;mp为颗粒质量，kg;cp为颗粒比热容，J/(kg·K);Ap为颗粒表面积，m2;Tf为连续相温度，K;h为对流传热系数，W/(m2·K);εp为颗粒辐射率;σ=5.67×10-8W/(m2/K4)为斯蒂芬孙-玻尔兹曼常数;θR为辐射温度，K;I为辐射强度，J/(cm2·min);Ω=4π 为空间立体角。

2.4 边界条件设定

模拟所需边界条件依据朝阳东大矿冶研究院悬浮磁化焙烧炉运行参数进行如下设置(表2～表4)。

表2 壁面参数设置Table 2 Setting of wall parameters

表3 进出口边界条件设置Table 3 Setting of import and export boundary conditions

表4 注入颗粒信息Table 4 Injected particle information

本研究以Fluent18.0为计算工具，各项计算残差以低于10-6为标准。计算过程中对出口z=1.5 m，z=3.5 m，z=5.5 m和z=7.5 m的截面温度以及气相平均速度进行监测，温度和速度达到恒定不再变化，并且满足残差要求即代表气相计算完成。随后，注入颗粒进行非稳态追踪，时间步长为0.05 s，继续迭代计算，直至完成颗粒相计算。

2.5 模型验证

空床条件下，通入甲烷气体在燃烧室内燃烧，悬浮磁化焙烧主炉内温度逐渐升高。通过控制甲烷气体给入量，控制悬浮焙烧主炉内的温度，采用全自动测温系统每间隔1 min记录下主炉上所有位点的温度。在同样的工况条件下，进行数值模拟计算，对比各截面数值模拟获得的温度与试验过程测得的温度，以此来验证传热模型和燃烧模型的准确性。

图3给出了4种甲烷气体给入量条件下，数值模拟与试验测得炉内温度数据的对比结果。由图3可知，数值模拟结果与试验结果的平均温差分别为25.48℃、27.38℃、37.05℃和81.58℃，相对误差分别为3.04%、2.93%、3.55%和6.44%。试验结果与模拟数据呈现出较好的吻合性，说明本文模拟计算所采用的模型具有一定的准确性。

图3 数值模拟数据与试验结果对比分析Fig.3 The comparison analysis of numerical simulation data and test results

3 数值模拟结果与分析

3.1 气相温度场的模拟结果与分析

图4、图5分别为主炉的轴向和径向温度分布云图。可以看出，悬浮焙烧主炉的中心处温度较高，而近壁端温度较低。由于热源(燃烧室)位于主炉底部，因此主炉底部温度较高，随着轴向高度的增加，主炉内温度逐渐降低且趋于均匀。

图4 主炉轴向温度分布Fig.4 Axial temperature distribution of main furnace

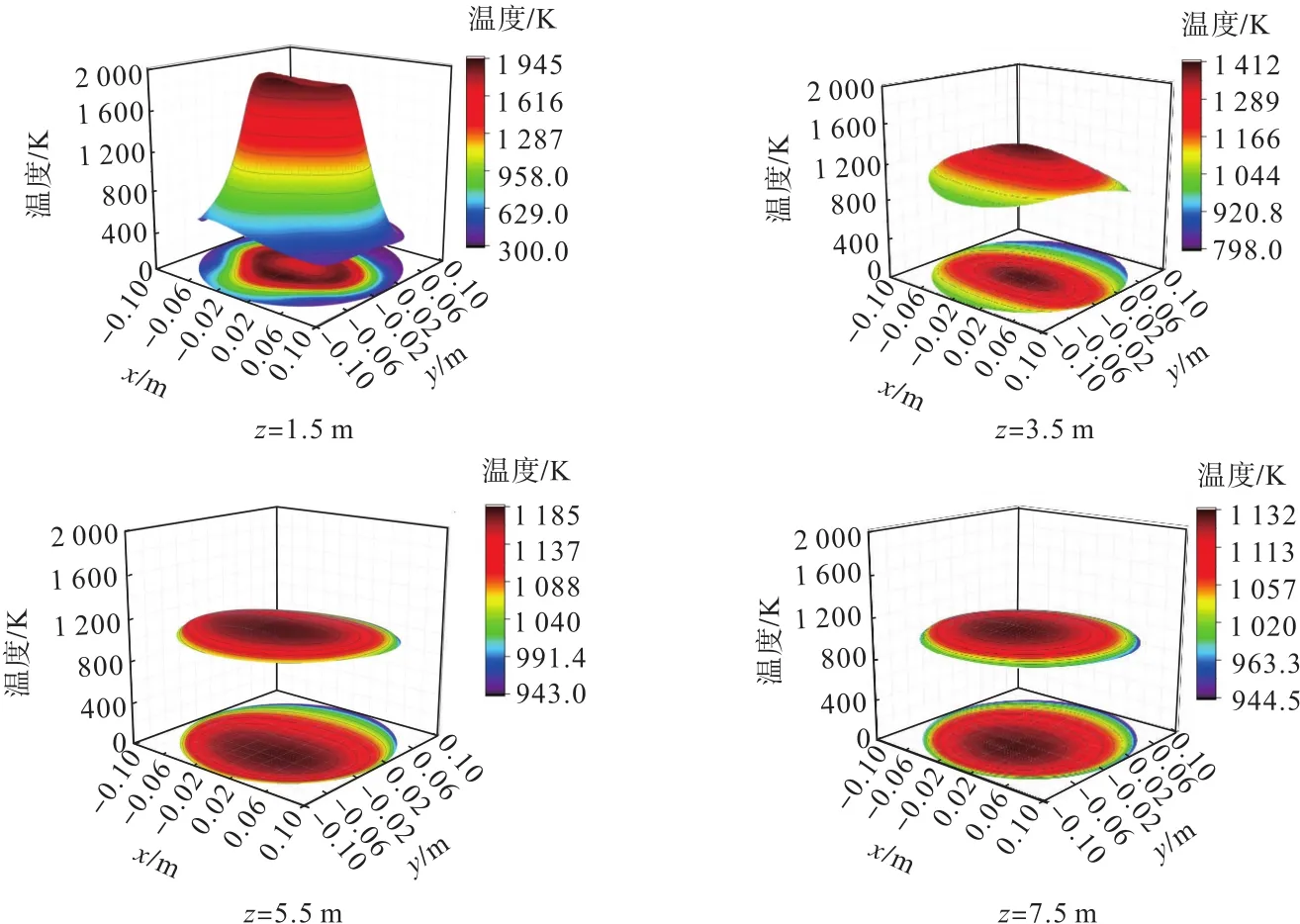
图5 主炉径向温度分布Fig.5 Radial temperature distribution of main furnace

3.2 颗粒运动模拟结果分析

图6为颗粒运动行为随时间变化情况，可以看出，颗粒进入悬浮焙烧主炉后在气流拖曳作用下迅速提升。1.0 s时，部分颗粒到达主炉顶部弯管附近，1.2 s时部分颗粒在弯管处开始出现逃逸现象。随着时间的延长，主炉内的颗粒数量逐渐增多，当逃逸颗粒数量与射入颗粒数量大致相当时，主炉中可以追踪到的颗粒数量处于动态平衡，说明主炉内气固两相流达到动态平衡状态。

图6 颗粒运动随时间的变化Fig.6 Change of particle flow with time

3.3 颗粒相温度模拟结果分析

图7为颗粒相温度变化曲线，可以看出，颗粒进入主炉后，颗粒温度在0.25 s内迅速达到最大值。随后，在沿轴向的提升过程中，颗粒的温度逐渐下降。这是由于主炉上部距离热源较远，气相温度较低，颗粒相和气相逐渐进行热量交换，导致颗粒温度逐渐降低。

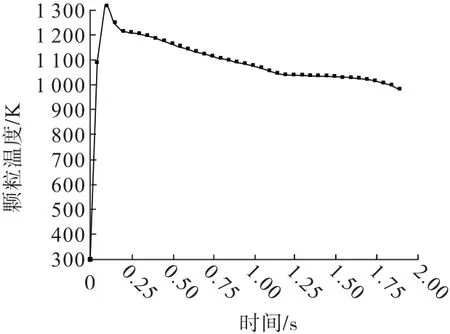
图7 颗粒相温度曲线Fig.7 Particle temperature curve

3.4 颗粒相停留时间模拟结果分析

图8为悬浮磁化焙烧主炉内颗粒的停留时间分布，可以看出，绝大多数的颗粒停留时间分布在1.1～8.0 s的范围内，每个颗粒在主炉的运动轨迹不同，导致其停留时间不同。总的来说，颗粒的停留时间呈现“早出峰、长拖尾”的分布特征[14]，95%以上的颗粒在悬浮磁化焙烧主炉内的停留时间处于1.2～3.6 s之间。

图8 颗粒停留时间Fig.8 Particle residence time

4 结 论

(1)悬浮磁化焙烧主炉内底部温度较高且高温区域处在炉中心，上部温度较低且温度区域均匀主炉内温度呈现“底部高、上部低””和“炉心高、近壁低”的特点;随着轴向高度的增加，温度分布在径向上的均匀度也有所提高。

(2)悬浮磁化焙烧主炉内颗粒子1.0 s到达主炉顶部，1.2 s时开始出现颗粒逃逸，2.0 s以后主炉内的气固颗粒流动达到动态平衡。此外，颗粒在主炉内停留时间分布呈现“早出峰、长拖尾”特征，95%颗粒停留时间处于1.2～3.6 s之间。

(3)颗粒进入悬浮磁化焙烧主炉后，处于主炉内高温区，颗粒在短时间内温度迅速上升达到最大值，随后随着轴向高度增加颗粒进入主炉低温区，气相和颗粒相不断进行热量交换，颗粒温度逐渐降低。